跷跷板系统干扰补偿的分层滑模控制策略研究
姜 堃,张井岗,沈云亮,邵雪卷
(1.山西晋中理工学院智能制造与车辆学院,山西 晋中 030600;2.太原科技大学电子信息工程学院,山西 太原 030024)
0 引言
跷跷板系统是一个典型的欠驱动系统,具有明显的非线性、强耦合性和不稳定性[1]等,是检验控制算法的理想试验平台。跷跷板系统的平衡控制原理与船舶平衡控制、飞行器姿态调整等实际系统有着很大的相似性。因此,对跷跷板系统控制策略的研究有着重要的理论和实践意义。
文献[2]以状态空间形式导出了带有状态反馈的跷跷板系统简化线性动力学方程。文献[3]利用拉格朗日方程建立了跷跷板系统数学模型。文献[4]针对跷跷板系统提出了一种基于模糊逻辑和协调器补偿的控制方法,并进一步提出了一种基于遗传算法的比例积分微分(proportional integral differential,PID)控制策略[5]。文献[6]提出了一种用单一模糊输入变量代替切换线的设计方法,大幅缩减了模糊规则数。但模糊控制器的设计通常受限于设计人员的经验,且由于非线性系统的不确定性以及外部干扰作用,模型的建立常存在不匹配的情况。
滑模控制(sliding mode control,SMC)的强鲁棒性使其对非线性系统有较好的控制效果。但在未知干扰作用下,为保证系统稳定,SMC通常需要保守设计较大的切换增益。文献[7]提出了一种基于未知扰动估计的切换增益自适应算法。文献[8]实现了对跷跷板模型的解耦,并通过径向基函数神经网络(radial basis function neural network,RBFNN)对系统受到的不确定干扰进行自适应逼近补偿。但以较少控制量来控制较多状态的欠驱动系统相当困难,且难以保证滑模面的收敛性。此外,神经网络样本训练是一个耗时的过程,过多的隐含层神经元也会使控制器设计变得复杂。基于干扰观测器的SMC律则简洁且易于设计。文献[9]提出了一种基于变增益超螺旋SMC和自适应模糊扰动观测器的复合控制策略,以提高双轴机载光电稳定平台在外部干扰影响下的跟踪性能。
考虑到实际工程中难以通过求导获取加速度信号的问题,本文设计了一种不包含系统状态二阶导信息的指数收敛干扰观测器,以对系统干扰进行估计补偿;针对跷跷板系统强耦合、欠驱动的特性,引入分层SMC,并通过模糊规则的设计实现切换增益自适应调节;在Matlab仿真环境和Quanser试验平台下,进行了SMC算法以及基于指数收敛干扰观测器干扰补偿的切换增益自适应模糊分层滑模控制(observer-fuzzy hierarchical sliding mode control,Obv-FHSMC)算法的仿真和试验,以检验所提复合控制算法在应用于跷跷板系统平衡控制时的有效性和可行性。
1 跷跷板系统动力学建模
跷跷板系统主体由小车、滑动导轨以及跷跷板倒三角体组成。其平衡机制是通过小车沿导轨运动改变系统重心,使跷跷板趋近并保持平衡。本文将跷跷板系统抽象成质点小车和匀质倒三角结构体的组合。跷跷板系统简化模型如图1所示。
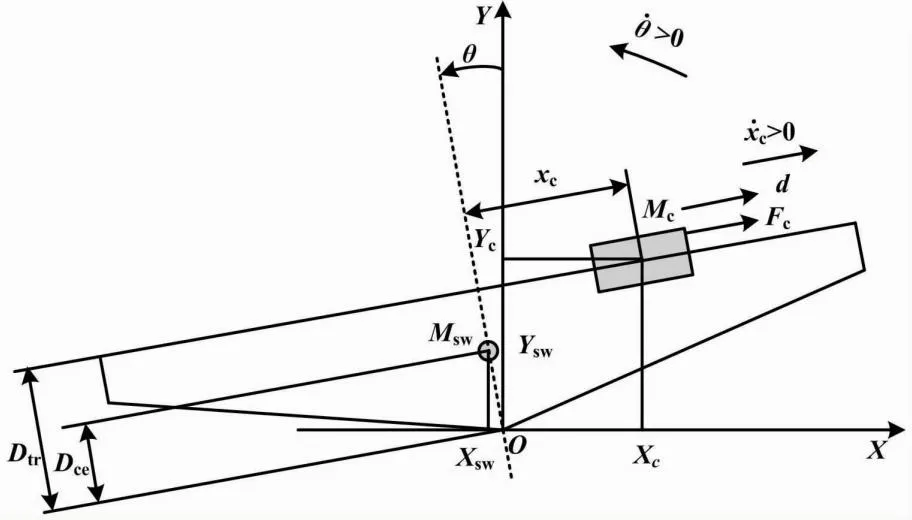
图1 跷跷板系统简化模型
本文定义xc(t)为小车偏离平衡点的位移、θ(t)为跷跷板倾斜角度、F(t)为小车驱动力、d(t)为跷跷板系统受到的干扰力、Dtr为小车轨道高度、Dce为系统重心高度、Msw为小车跷跷板系统质量、Mcr为小车质量、Jsw为系统转动惯量、Beq为小车齿轮等效阻尼系数。
本文根据拉格朗日方程建立跷跷板系统动力学模型。根据图1建立的XOY坐标系,跷跷板结构体重心位置(Xsw,Ysw)和小车重心位置(XC,YC)分别为:
(1)
(2)
系统总动能T为:

(3)
本文定义X轴为零势能点,则系统总势能Vpe为:
Vpe=McrgYC+MswgYsw=Mcrg[xc(t)sinθ(t)+
Dtrcosθ(t)]+MswgDcecosθ(t)
(4)
本文取拉格朗日算子L=T-Vpe,并忽略跷跷板绕轴心转动的摩擦力、空气阻力,所建立的拉格朗日方程为:
(5)
式(3)、式(4)代入式(5),可得:
(6)
求解式(6),并在系统平衡点处通过求解雅可比矩阵将模型线性化[10],可得:
(7)
(8)
2 复合控制算法设计
跷跷板系统控制结构如图2所示。
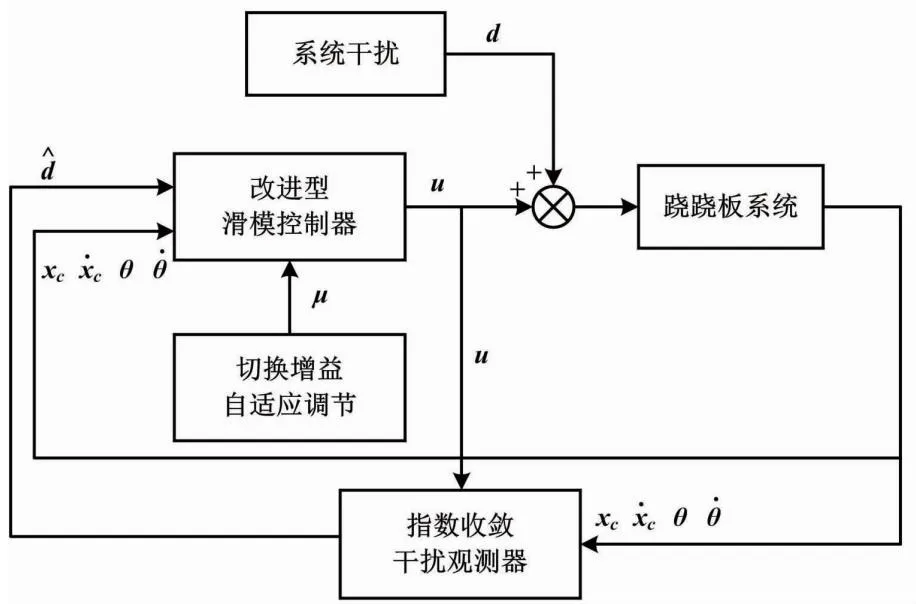
图2 跷跷板系统控制结构框图
跷跷板系统主体呈现倒三角形,下方只有单一支点而整个结构的重心在上方。这就使得其本质是一个不稳定系统,在面对干扰时极为敏感。当控制小车产生位移时,由于跷跷板整体的结构特性,势必会引起跷跷板倾斜角度的变化,导致整个系统表现出很强的耦合性。此外,控制系统要求通过单一输入量(即电机对小车的驱动力),来实现对小车位移以及跷跷板倾斜角度等多个变量的控制。这样的欠驱动特性也是跷跷板系统平衡控制的一大难点。
针对跷跷板系统的上述特性,本文提出一种指数收敛干扰观测器与切换增益模糊自适应分层SMC相结合的复合控制策略。
2.1 指数收敛干扰观测器设计
系统状态空间表达式如下。
(9)
式中:aij、bij分别为A、B矩阵对应位置的元素。
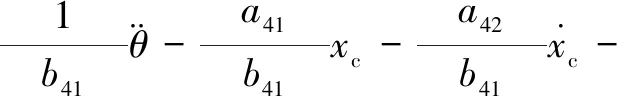
(10)
设计干扰观测器的一般思想,是用估计输出与实际输出的差值对估计值进行修正,即:
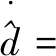
(11)
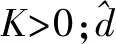
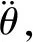
(12)
则:
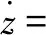
设计改进后的干扰观测器为:
(13)
由式(13)可得:

(14)

设观测误差为:
则:
(15)
式(14)代入式(15),可得:
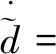
(16)
2.2 分层SMC算法设计
本文将式(9)转化成以下标准形式:
(17)
由式(17)可知,小车位移与跷跷板倾角的运动构成了一个四阶非线性耦合欠驱动系统。为此,本文考虑引入分层滑模方法来控制该系统。控制目标为[x1,x2,x3,x4]→[xo1,xo2,xo3,xo4]。其中:xoi为各状态变量的期望值,是常量。针对式(17)所描述的跷跷板系统,本文将其看作两个2阶子系统的耦合。两个子系统分别为小车系统(x1,x2)和跷跷板倾角系统(x3,x4)。
状态误差为ei=xi-xoi,i=1,2,3,4。所构造的第一层滑模面为:
(18)
式中:c1>0、c2>0均满足Hurwitz条件。
对式(18)求导,可得:
(19)
根据Filippov等效控制理论,将式(9)代入式(19),可得两个子系统在其各自滑动平面上的等效控制量:

(20)
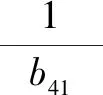
(21)
为保证各子系统能分别进入其各自的滑动平面,并沿各自滑动平面作滑模运动,必须使总滑模控制律中包含各子系统的等效控制量[11]。为此,本文设计的总滑模控制律为:
u=ueq1+ueq2+usw
(22)
式中:usw为系统在趋近阶段的切换控制量。
所构造的第二层滑模面为:
s=αs1+s2
(23)
式中:α为常数。
α满足:
(24)
式中:α0>0。
(25)
式(9)、式(22)代入式(25),可得:
ueq2+usw)+b21d]+[a41x1+a42x2+a43x3+(c2+
a44)x4+b41(ueq1+ueq2+usw)+b41d]=αb21(ueq2+usw+
(26)
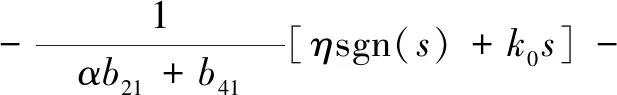
(27)
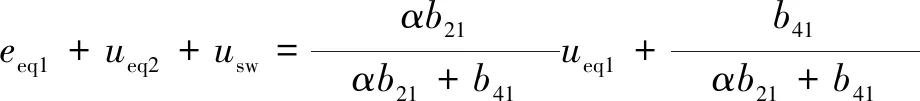
(28)
2.3 切换增益调节系数的模糊自适应设计
滑模控制律中,等效控制可以使系统状态保持在滑模面上运动;切换控制则可以迫使远离滑模面的系统状态向滑模面作趋近运动,以保证SMC的鲁棒性。如果切换控制的切换增益较小,则系统状态趋近滑模面时的速度较小,引起的系统抖振也较小;如果切换控制的切换增益较大,则系统状态到达滑模面时的速度也较大,引起的抖振也相应变大。
因此,切换增益调节系数的调节原则应为:当系统状态距滑模面较远处时(或者说受到较大干扰时),宜选取较大的切换增益调节系数,以保证快速趋近;当系统状态在滑模面附近时(或受到的干扰较小时),宜选取较小的切换增益调节系数,以减弱抖振[12]。为此,可以通过设计模糊规则来实现切换增益的自适应调节。
本文将式(27)设计的切换控制量改进如下。
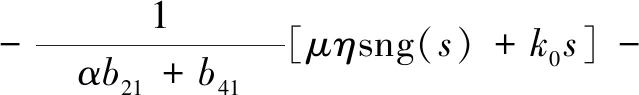
(29)
式中:μ为切换增益调节系数,μ≥0。
模糊逻辑系统的设计过程如下。
①确定模糊系统的输入变量为s,并以μ作为输出变量。
②定义模糊集合及其隶属函数。本文对s定义Z、N和P三个模糊集,对μ定义Z、P两个模糊集。Z、N和P分别表示“零”“负”和“正”。根据实际情况,通过比例因子将模糊集论域统一为[-1,1]。s中的N、P模糊集采用梯形隶属函数,Z模糊集采用三角形隶属函数。μ的两个模糊集均采用梯形隶属函数。
③模糊规则的设计。基于切换增益调节系数的调节原则,为保证s→0,模糊规则制定为:
ifs(t) isNthenμisN
ifs(t) isZthenμisZ
ifs(t) isPthenμisP
第二行规则表示当没有干扰(系统状态处于滑模面上)时,μ=0。此时,控制律不包含符号函数,系统保持滑模运动。第一、第三行规则表示,系统受到干扰时,μ≠0。此时,控制律中切换控制量增大,系统进行趋近运动。
④解模糊。本文采用重心法进行解模糊。
综上所述,通过模糊系统的输出,即切换μ的自适应变化,可以实现对切换增益的调节,从而削弱系统抖振。
2.4 稳定性分析
本小节将逐步证明所构造的两个分层滑模面的稳定性以及系统的李雅普诺夫稳定性。在此先给出分析过程中涉及到的两个引理。
①Barbalat引理1。

②Barbalat引理2。
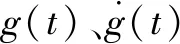
2.4.1 第二层滑模面s的稳定性分析
式(29)代入式(26),可得:
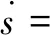
(30)
定义闭环系统的李雅普诺夫函数为:
(31)
则:
(32)
式(30)代入式(32),可得:
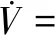
(33)
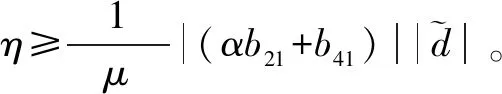
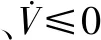
对式(33)两边同时取积分,则:

(34)
因为V(t)≥0,所以有:
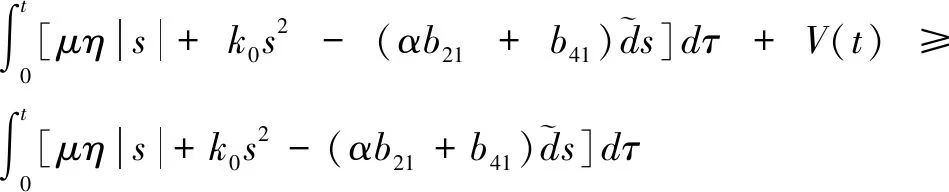
(35)
从而可得:
V(0)<∞
(36)
以下将进一步分析,在s=0全局渐近稳定的前提下,s1和s2的渐近稳定性。
2.4.2 第一层滑模面s1、s2的稳定性分析
根据Barbalat引理2,本文要证明t→∞时的s1、s2平方可积,即:
(37)
由式(36)可知:
(38)
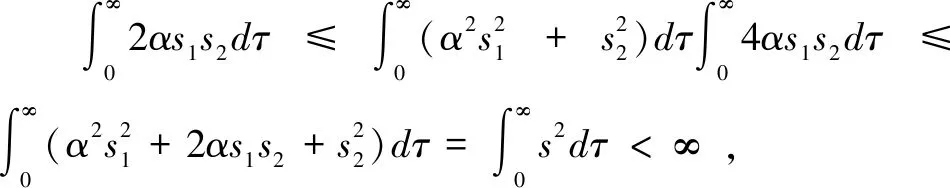
(39)
由于s=αs1+s2,且式(24)中的α选取保证了αs1s2≥0,即αs1与s2同号。结合式(39),可得:
(40)

(41)

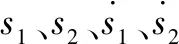
3 仿真与试验
3.1 仿真及分析
在Matlab环境下,针对跷跷板系统,本文分别采用传统SMC算法和Obv-FHSMC算法进行仿真验证。
跷跷板系统各参数取值为:Msw=3.6 kg;Dt=0.125 m;Jsw=0.395 kg·m2;Beq=4.3 N/(m/s);DC=0.058 m;MC=0.57 kg。
系统干扰及观测器的估计曲线如图3所示。

图3 系统干扰及观测器的估计曲线
由图3可知,估计曲线仅在个别局部区间上与实际干扰曲线存在较小误差,整体上与干扰曲线保持一致。这体现了所设计干扰观测器良好的收敛精度和对干扰的精确估计能力。Matlab环境下跷跷板平衡控制仿真曲线如图4所示。
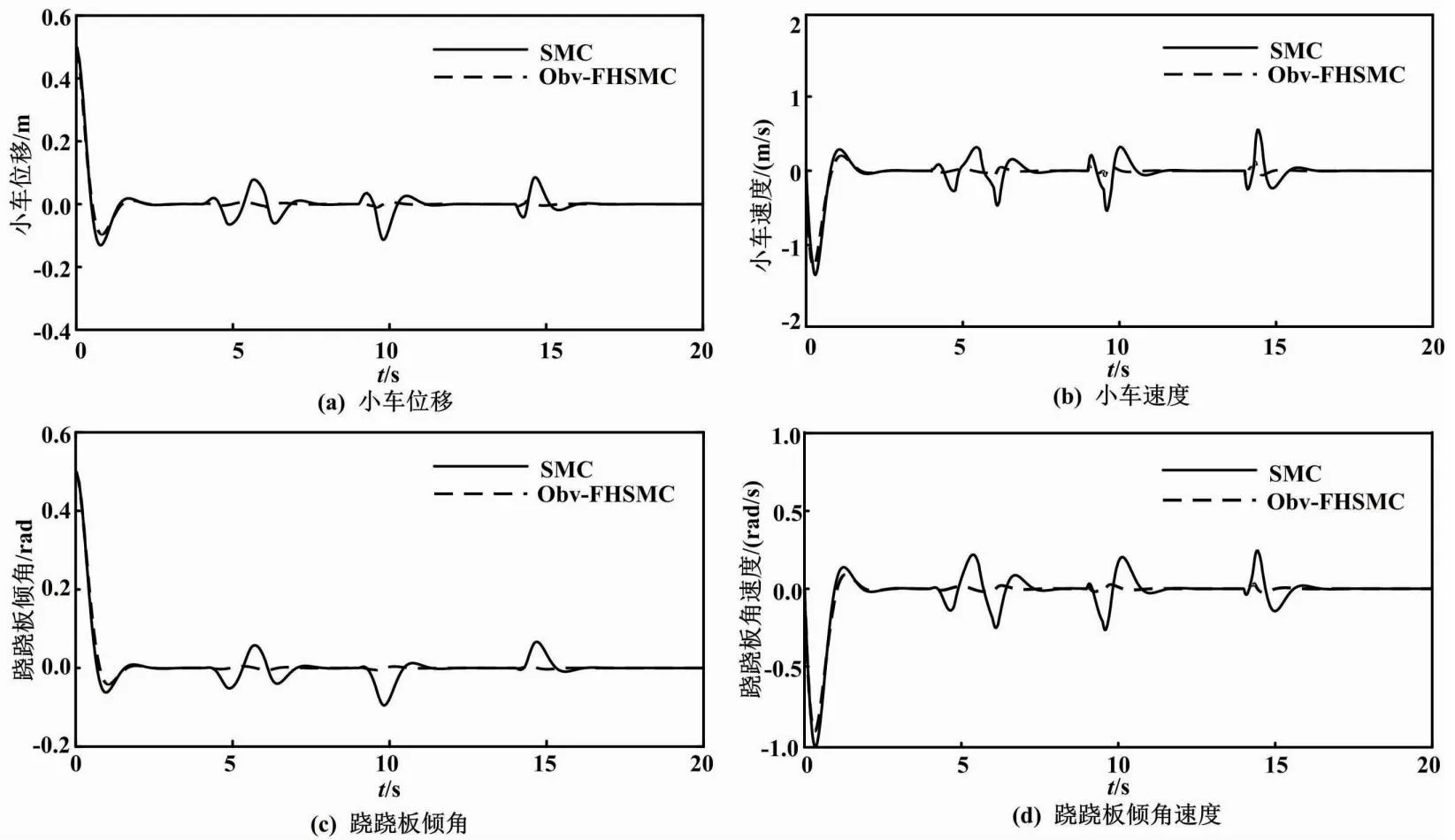
图4 Matlab环境下跷跷板平衡控制仿真曲线
由图4可知,增加了干扰补偿的Obv-FHSMC曲线相较于SMC曲线,系统到达平衡状态所需要的时间更短;在4~6 s、9~10 s以及13~14 s区间上,与相同区间下的较大外部干扰相对应,SMC曲线大幅偏离了平衡位置,而Obv-FHSMC曲线仅在平衡位置附近作小幅波动。这体现了Obv-FHSMC算法具有更强的抗干扰能力和更快的收敛速度。
SMC算法和Obv-FHSMC算法的控制器输出曲线对比如图5所示。

图5 控制器输出曲线对比
由图5可知,具有切换增益模糊自适应调节的Obv-FHSMC曲线抖动程度更低。这在一定程度解决了传统SMC算法在未知大干扰下切换增益过大的问题。
3.2 试验及分析
本文采用Quanser公司提供的跷跷板系统试验平台。试验时先将跷跷板和小车置于平衡位置,启动试验装置;待跷跷板系统保持平衡状态后向导轨施加不同方向的干扰力,以检验控制算法的抗干扰能力。
Quanser试验平台下跷跷板系统实时控制响应曲线如图6所示。

图6 Quanser试验平台下跷跷板系统实时控制响应曲线
Quanser试验平台下控制器输出曲线如图7所示。
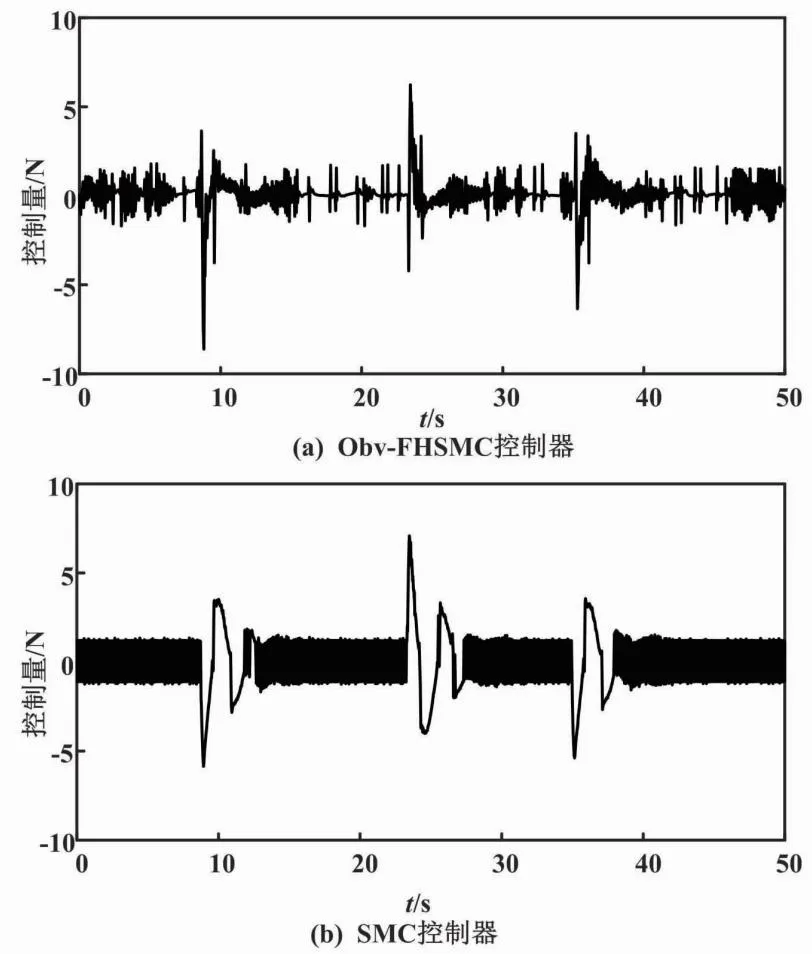
图7 Quanser试验平台下控制器输出曲线
由图7可知,具有切换增益模糊自适应调节的Obv-FHSMC算法曲线的抖动程度更低。这能够在一定程度上解决传统SMC算法在未知大干扰下的抖振问题。
试验在10 s、24 s、36 s左右对跷跷板系统施加不同程度、方向的干扰力。虽然两种算法在受到干扰影响时都偏离了平衡位置,但增加了干扰补偿的Obv-FHSMC响应曲线相比于SMC响应曲线收敛速度更快(收敛时间缩短约28%),且Obv-FHSMC响应曲线的偏离程度和波动幅值也均小于SMC响应曲线。
4 结论
针对跷跷板这类不稳定、强耦合的欠驱动系统,本文将外部扰动对跷跷板系统平衡控制的影响纳入考虑,在Simulink仿真环境以及Quanser试验平台下,验证了基于指数收敛干扰观测器干扰补偿的切换增益模糊自适应分层SMC算法在应用于跷跷板系统平衡控制时的有效性和可行性。为应对跷跷板系统耦合欠驱动特性,本文采用了分层SMC算法,并通过模糊规则的设计实现了切换增益的自适应调节;为提高跷跷板系统的抗干扰能力,设计了一种指数收敛干扰观测器对系统受到的外部扰动等不确定因素进行估计补偿,实现了未知大干扰下跷跷板系统的平衡控制。此外,该干扰观测器不需要系统状态变量二阶导信息,解决了实际工程中难以通过求导获得加速度信号的问题。本文所提出的复合控制策略也可以应用于类跷跷板平衡控制的实际系统中。

