基于q 轴电流补偿的牵引电机拍频抑制方法研究
蒋 威,王全宇,殷振环,郭永琪,宋文胜
(1 中国铁道科学院研究院集团公司 机车车辆研究所,北京 100081;2 北京纵横机电科技有限公司,北京 100094;3 西南交通大学 电气工程学院,成都 611756;4 动车组和机车牵引与控制国家重点实验室,北京 100081)
当前,我国动车组和机车已进入以轻量化、节能化为目标的新发展阶段。动车组和机车电力牵引传动系统主电路普遍采用交—直—交拓扑结构,如图1 所示[1]。在该系统拓扑下,单相整流的工作特性导致牵引变流器中间直流环节电压含有2 倍电网频率的脉动分量。当电机定子频率接近2倍电网频率时,直流侧电压2 倍网频脉动分量的存在会引起电机转矩剧烈波动、电机电流畸变严重、功率损耗急剧增大等问题,即拍频现象,严重威胁列车安全运行[2-4]。
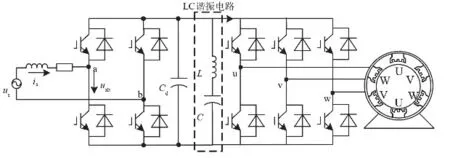
图1 交—直—交电力牵引传动系统电路拓扑
为抑制拍频现象,简单有效的方法是在中间直流环节并入可以吸收直流电压2 倍网频脉动分量的LC 谐振电路。由于该运用条件下电感元件功率密度较低,因此谐振电路本身具有较大的体积和质量。在不额外增加硬件设备的情况下,通过特定的控制策略也可以实现拍频现象的抑制[3-4]。在新一代牵引系统的研发过程中,对缩减体积和质量的需求极为迫切,取消LC 谐振电路具有非常重要的工程价值。
文中在研究既有拍频抑制方法[5-14]的基础上,首先分析了直流侧电压脉动对q轴电流的影响规律,进一步研究了一种基于q轴电流进行补偿的拍频抑制策略及其具体实现方法,最后对该拍频抑制方法进行了半实物仿真测试验证以及对相应结果的分析。
1 直流侧电压脉动对q 轴电流影响分析
电力牵引系统网侧采用单相整流方式的情况下,直流侧输出电压可表示为式(1)[13]:
式中:Udc为直流侧电压平均值;ΔUdc为直流侧脉动电压幅值;ωrp为直流侧脉动电压角频率;φ为直流侧脉动电压相位。
将变流器开关器件视为理想开关,则三相逆变器开关函数Si(t)[3]可表示为式(2):
式中:ωs为逆变器工作角频率;Aik为逆变器i相桥臂开关函数的第k次谐波幅值系数(k为奇数);φu=0;φv=-2π/3;φw=2π/3。
进一步将逆变器输出相电压uio为式(3):
可以看到,式(3)右侧第1 项为中间直流侧电压稳态值产生的分量,第2 项为直流侧脉动电压叠加产生的分量。由于系数Aik反比于kωs,即谐波分量次数越高、幅值越小,因此对拍频现象起主导作用的是低次分量,即角频率为ωrp±ωs的电压分量相对影响更大。
通过对逆变器输出电压进行坐标变换,可获得在d-q同步旋转坐标系下的定子电压为式(4):
结合式(1),则有式(5):
式中:、分别为直流侧电压平均值产生的d轴、q轴电压分量;Δudr、Δuqr分别为脉动电压产生的d轴、q轴电压分量。
牵引异步电机等效电路如图2 所示。
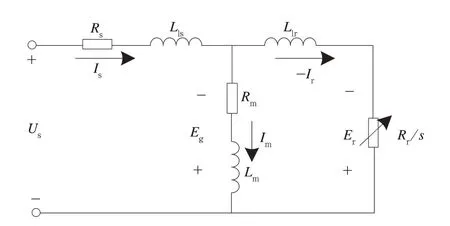
图2 牵引异步电机等效电路
根据等效电路,可得电机等效阻抗系数[14]为式(6):
式 中:Ls、Lr分别为电机的定、转子电感;Lm为电机的互感;Rs为电机的定子电阻;ωs1为转差角频率。
根据式(6)可得到逆变器输出电流d轴id和q轴分量iq表达式为式(7):
矢量控制策略下,牵引电机的输出转矩Te为式(8)、转子磁链ψr为式(9):
式(9)中的转子时间常数Tr相对较大,为简化分析可以忽略d轴电流脉动分量所引起的磁链脉动量,则电机输出转矩可进一步表示为式(10):
式中:Δiqr为q轴电流脉动分量。
根据式(10)可知,Δiqr的存在会造成电机输出转矩中也存在脉动分量。根据式(5)与式(7),令s=jωrp,得到Δiqr为式(11):
由式(11)可知,逆变器频率ωs越接近拍频频率ωrp,Gk(jωrp)越小,Δiqr分量越大,则电机转矩脉动越大,拍频现象越严重。
2 基于q 轴电流补偿的拍频抑制方法[14]
要实现拍频抑制,根据伏秒平衡原理,可以对牵引逆变器输出频率叠加一个体现脉动分量的补偿量[7],如图3 所示。
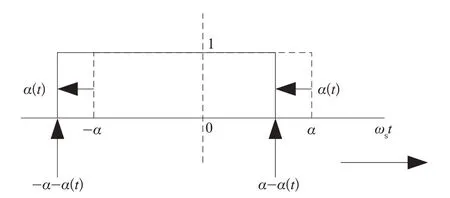
图3 逆变器频率叠加补偿量的示意图
图3 中,α(t)为体现脉动分量的补偿量为式(12):
式中:ΔFr为补偿系数;φr为补偿函数相位。
逆变器瞬时工作角频率可表示为式(13):
根据式(13),补偿量引起的逆变器输出电压分量可表示为式(14):
式中:Δudc、Δuqc分别为频率补偿量所引起的逆变器输出电压d、q轴电压分量。
根据式(11)类推可得到频率补偿引起的q轴电流分量,为式(15):
综合式(11)与式(15),当频率上加入补偿量时,q轴电流脉动量可分为两部分,一部分由直流侧电压脉动引起,另一部分由补偿量引起。q轴电流脉动量表达式为式(16),根据式(16)可知,可通过调节Δiqc抵消Δiqr,从而减小Δiq的幅值,达到拍频抑制的目的。
将式(14)代入式(15),得到Δiqc为式(17):
通过补偿系数ΔFr可调整Δiqc的幅值。引入补偿器Gc(jωrp),使2πΔFrsin(ωrpt+φ)=Δiq×Gc(jωrp),联立式(16)、(17)可得到q轴电流脉动量表达式为式(18):
若补偿器Gc(jωrp)对ωrp的传递函数增益较大,使式(18)中的分母项具有较大值,则无论逆变器的工作条件如何,Δiq项都可以被抑制,因此可采用式(19)所示的传递函数作为控制器:
式(19)的控制器虽然在谐振频率点处有高增益,但频带很窄,在非谐振频率点处增益低,使得该控制器无法抑制非谐振频率点的干扰信号,在实际应用中不利于保持系统的稳定性,因此将控制器改进为式(20):
式中:ωc为增益带宽参数;Kr为谐振增益。
基于q轴电流补偿的拍频抑制方法的实现如图4 所示,其中具体补偿过程如下:反馈的q轴电流经过补偿器Gc(s)后输出角频率补偿量Δωsl,将其与计算的定子频率ωs叠加后输出补偿后的定子频率ωs’,对ωs’进行积分得到转子磁链位置角φ参与矢量控制。
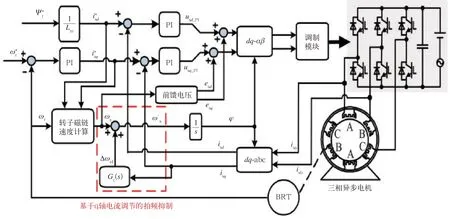
图4 基于q 轴电流补偿的拍频抑制方法实现框图
3 半实物仿真测试验证
为验证所研究方法的正确性与有效性,利用HIL 半实物仿真平台对其进行测试验证。采用的电机参数见表1,电机控制方法采用图4 所示的矢量控制策略,逆变器调制采用异步调制+多模式分段同步调制方式。仿真过程中直流侧电压叠加有峰—峰值为200 V、频率为100 Hz 的交流电压分量。
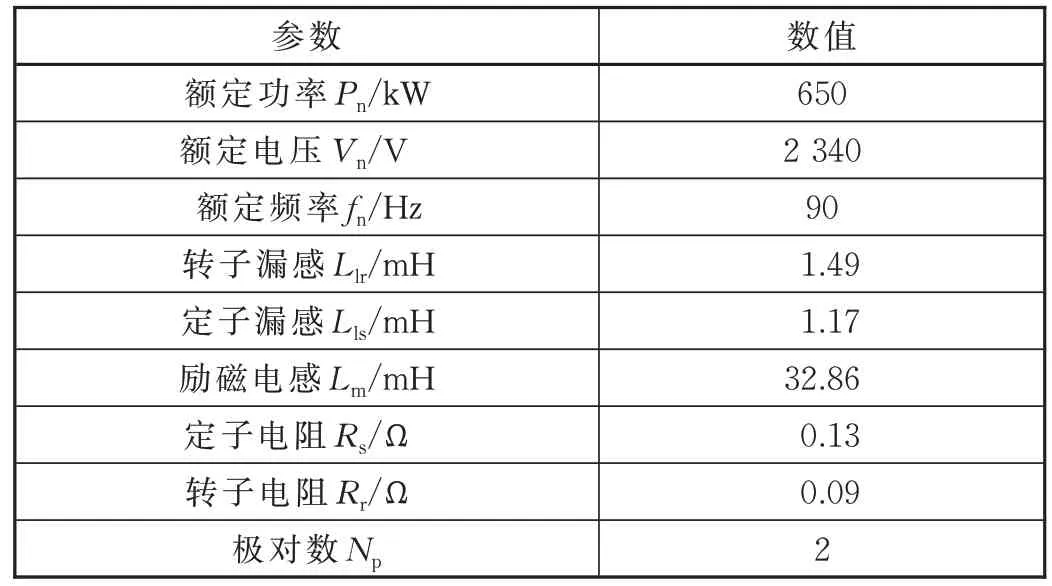
表1 仿真测试采用的电机参数
全速域工况下,无LC 谐振电路且未进行拍频抑制时,牵引电机的输出转矩、电流及转速波形如图5(a)所示,图中Te为电机转矩;is为电机电流;wr为转速。可见,当定子频率接近100 Hz 时,电机输出转矩脉动大,电流畸变严重。全速域工况下,无LC 谐振电路且采用所研究拍频抑制方法时的半实物仿真结果如图5(b)所示。显然,当定子频率接近100 Hz 时,电机转矩脉动明显减小,电流畸变情况得到明显改善。

图5 全速域工况下的电机转矩、电流、转速波形
电机处于牵引工况且定子频率稳定为98 Hz时,输出转矩和电流的波形对比如图6 所示。由图6(a)可知,不进行拍频抑制时,电机转矩脉动约为3 500 N·m;由图6(b)可知,采用所研究拍频抑制方法后,转矩脉动减小至850 N·m。电机电流FFT分析结果如图7 所示,可以看到,所采用的方法可将2 Hz 谐波含量由58%降低至5%,有效实现了拍频抑制。
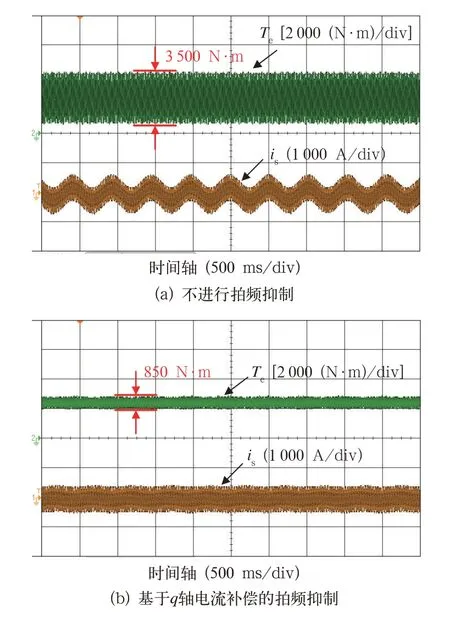
图6 定子频率98 Hz 时电机转矩、电流波形

图7 定子频率98 Hz 时电机电流FFT 分析
电机处于牵引工况且定子频率稳定为102 Hz时,输出转矩和电流的波形如图8 所示。由图8(a)可知,不进行拍频抑制时,电机转矩脉动约为3 400 N·m;由图8(b)可知,采用所研究拍频抑制方法后,转矩脉动减小至850 N·m。电机电流FFT分析结果如图9 所示,可以看到,所采用的方法将2 Hz 谐波含量由57% 降低至5%,拍频抑制效果显著。
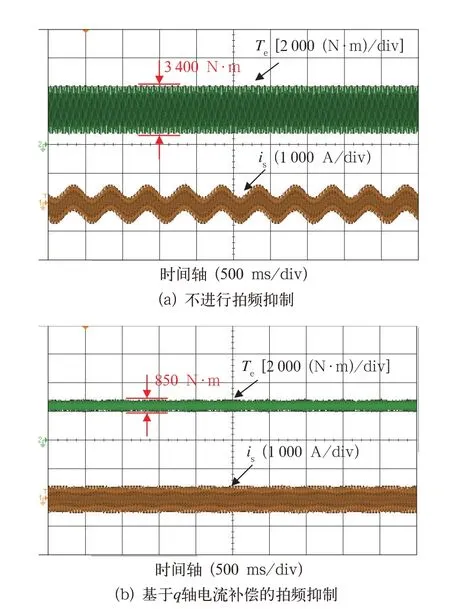
图8 定子频率102 Hz 时电机转矩、电流波形

图9 定子频率102 Hz 时电机电流FFT 分析
4 结论
文中针对电力牵引变流器中间直流环节取消LC 谐振电路的应用需求,研究了一种基于q轴电流补偿的拍频抑制方法。相应的测试验证结果表明,该方法在电力牵引传动系统全速域范围内具有较为显著的拍频抑制效果,极大程度降低了中间直流侧电压2 倍网频脉动分量对牵引电机输出转矩和电流的不利影响,可以有效保证系统的正常运行。该拍频抑制方法易于工程实现和应用推广,为实现牵引传动系统的轻量化目标提供了有效的技术手段。

