NaF-AlF3体系热导率的有限元数值模拟

肖镭， 赵雪， 王聪， 高炳亮

（东北大学冶金学院， 沈阳 110819）

对铝电解质物理化学性质的研究不仅有助于了解铝电解质熔盐体系的结构，而且可以为铝电解生产技术提供理论依据。热导率作为铝电解质的一个重要物性参数，其在电解槽的热平衡计算中至关重要。有效的热场分布计算有助于高效评估电解槽的热平衡状态，以及建立工艺参数与电解槽侧部炉帮厚度的内在联系，进而达到提高电流效率和延长电解槽服役寿命的目的。

在有关固态/液态无机盐及多元混合物的热导率相关研究中，研究方法主要分为仪器测量和数值模拟2种。仪器测量方法有同轴圆柱体稳态测量法[1]、激光闪光法[2]、瞬态热线法[3]、强制瑞利散射法[4]和热通量差示扫描量热法（DSC）[5]等。数值模拟法包括平衡分子动力学法（EMD）[6]、非平衡分子动力学法（NEMD）[7]、反向非平衡分子动力学法（RNEMD）[8]和第一性原理法（FPMD）[9]等。研究者使用这些热导率实验测量和数值模拟计算方法，用于构建单组元和多组元熔盐的热导率预测模型[10-14]。

NaF-AlF3二元体系是铝电解质的基础体系。KHOKHLOV等[15]采用稳定圆柱温度梯度的实验方法，测量了该体系初晶温度附近不同分子比（体系中NaF与AlF3的摩尔比，简写为CR）的31种组成的热导率数据，用回归曲线的方法，建立了含量与液态熔盐热导率之间的联系。

GHERⅠBⅠ等[16]利用密度泛函理论（DFT）中的EMD方法结合晶型分析，对NaF-AlF3二元体系中存在的3种冰晶石晶型：563 ℃（836 K）以下的α-冰晶石单斜结构低温相、563 ℃（836 K）以上的β-冰晶石立方结构高温相，以及由冰晶石相通过包晶转化而来的亚冰晶石相等，建立了各种结晶相的热导率与温度的表达式（1）。GHERⅠBⅠ等[17]证明：在200～537 ℃（473～810 K）温度范围内，无论是混合多晶相体系还是单结晶相体系，热导率与温度均成反比关系，见式（1）。

LV等[18]同样利用密度泛函理论（DFT）中的NEMD方法结合白金汉势模型，建立了NaF-AlF3二元体系不同分子比条件下配位结构与热导率的联系。

有限元分析法已经被广泛地用于研究热交换过程[19-20]。程友良等[21]采用Fluent有限元分析软件研究了相变材料的导热系数和熔点对蓄热单元热传输效率的影响，得到了热传输效率最高的相变材料熔点值。OPPELT等[22]利用有限元分析法研究了相变材料的颗粒形状、粒度分布、空间取向等对有效热导率的影响。结果表明，三维模型比二维模型的分析结果更精确，原因在于其降低了二维模型因不考虑颗粒的各向异性而导致的显著分析误差。

对物理实体的热场分析而言，准确的热导率显然对获得准确的模拟结果非常重要。对于实际的冶金过程和换热过程而言，部分材料的组成不是稳定不变的。例如，铝电解槽绝缘侧壁上的固态电解质会随着液态电解质成分和电解温度的改变而变化。要建立电解质组成和温度与固/液态电解质热导率之间的函数关系，显然需要做大量的系统测试工作。如果能够设计一种传感器，在电解槽运行过程中，现场取样分析，获得电解槽中电解质的固/液态热导率，则对电解槽的热平衡控制更有意义。本论文介绍了一种研究固/液态无机盐热导率的新方法。通过热分析传感器采集液态无机盐在冷却过程中的温度变化数据，利用ANSYS Fluent有限元分析软件模拟固/液态无机盐的冷却行为，通过不断优化数值模型中热导率函数来调整实验数据和数值模拟数据的偏差，将最小偏差下的热导率函数确定为所测熔盐的热导率。通过该方法，本文获得了NaF-AlF3体系热导率K与温度T-2/3之间的比例系数变化，建立了NaF-AlF3体系热导率（K）、温度（T）和分子比（CR）之间的联系。

1 实验部分

1.1 热分析实验

热分析实验所用传感器的结构如图1所示：传感器内嵌2个K型热电偶：一个热电偶的测量端安置在熔盐样品杯中，用于测量熔盐在冷却过程中的温度变化；另一只热电偶安置在不锈钢实心柱体中，在测量过程中充当参比热电偶。两只热电偶的冷端与温度采集模块相连，将温度模拟信号转换成数值信号输送给计算机，用于后续分析。温度采集模块采用美国国家仪器公司的NⅠ9211热电偶模块，通过USB串口数据线与计算机相连，温度数据的采集频率为2.5 Hz。

图1 热分析传感器的结构Fig.1 Schematic structure of thermal analysis sensor

热分析实验中所用的化学试剂皆为纯度不小于99 %的分析纯试剂，使用前在400 ℃干燥3 h，冷却到室温后保存于120 ℃的恒温烘干箱内。不同分子比的二元铝电解质由氟化钠和氟化铝按照化学计量比配制而成。

热分析实验中[23]，将700 g熔盐置于高纯石墨坩埚内，在电阻炉内加热到实验温度。待熔盐完全熔化后，将传感器浸没在熔盐中直到温度达到实验温度，然后将传感器从坩埚内取出，置于空气中冷却至277 ℃（550 K），在整个过程中记录传感器中两只热电偶的温度数据。

图2中给出了分子比分别为3.0、2.7和2.4的NaF-AlF3熔盐体系的热分析实验曲线，分别在999.3 ℃（CR=3.0）、996.4 ℃（CR=2.7）和990.6 ℃（CR=2.4）位置出现了平台，这是因为熔体中有冰晶石固体相析出，同时释放出结晶潜热。

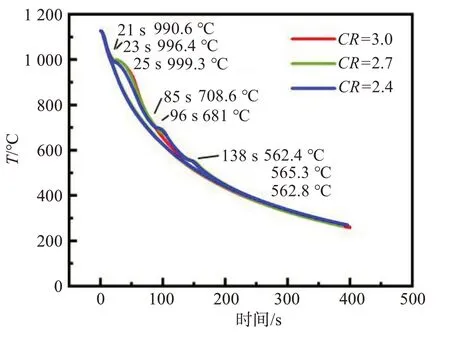
图2 不同分子比的冰晶石热分析实验对比Fig.2 Comparisons of thermal analysis data for cryolites at various CR

随着体系温度持续下降，部分固态冰晶石会转化为固态亚冰晶石，这种相变行为对应热分析曲线中700 ℃（973 K）左右位置出现的平台，亚冰晶石相的出现与否与电解质分子比密切相关，分子比越低，固相中出现的亚冰晶石含量越多，相应的相变潜热越大，该位置的平台越明显。

在563 ℃（836 K）左右，剩余固态冰晶石相会从β立方晶相转化为α单斜晶相，因此导致热分析曲线的斜率在138 s时均出现了明显的变化，其对应的放热平台分别为562.8 ℃（CR=3.0）、565.3 ℃（CR=2.7）和562.4 ℃（CR=2.4）。

1.2 有限元模型的构建

本文利用有限元体积法，使用ANSYS/Fluent软件中的流体体积模块（VOF）、离散坐标辐射模块（DO）和熔化/凝固模块对传感器物理实验进行仿真模拟。

传感器探头上连接的不锈钢管的壁厚为0.2 mm。前期热场模拟表明，通过管壁的热流量在总的散热流量中占比不超过5 %，为减少模型计算量，在构建3D几何模型时仅仅考虑了热分析传感器的探头部分，如图3所示。将探头周围的空气域设置为一个六面立方体，空气域的底面设置为探头的物理支撑面，其余5个面设置为压力出口。计算前，空气域的初始温度为27 ℃（300 K），传感器域和熔盐域的初始温度均为1 127 ℃（1 400 K）。

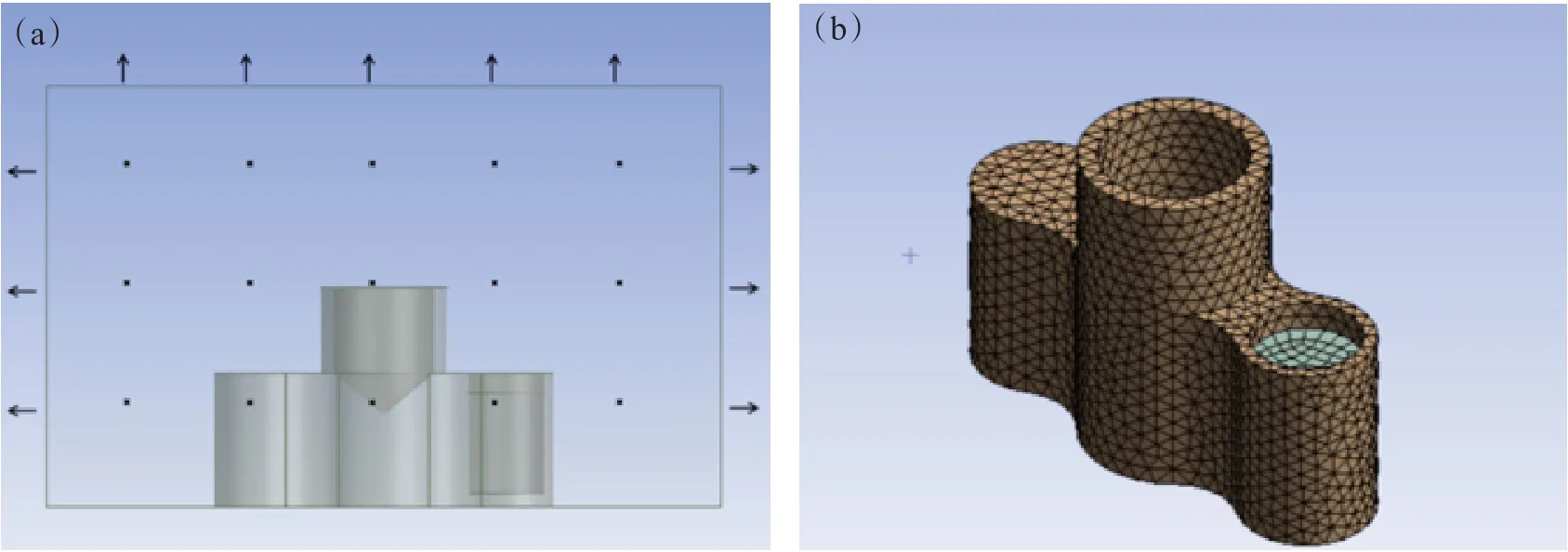
图3 热分析传感器探头的3D模型：（a） 传感器模型；（b） 网格划分Fig.3 3D model of thermal analysis sensor head：（a）modeling of the sensor; （b） meshing of the sensor

能量方程式（2）中能量ρE的变化与热传导k∇T、物质扩散-∑hJ→、黏性耗散τv→和压力功-v→(ρE+p)以及热源S等项相关。

式（2）中：ρ为密度；E为单位质量总能量；k为导热系数；T为温度；h为物质的焓；J为扩散通量；τ为黏性剪应力；v为流速；p为压强；S为热源。

本研究考察了氯化钠和NaF-AlF3二元体系的热行为，热源S定义为熔盐在冷却过程中释放出的结晶潜热和相变潜热，热源增加区域限定在如图4黑色边框区域，通过热分析实验获得潜热放热时间，并利用CHASE等[24]中的潜热数据计算获得其所涉及的各种热源S的数值，总结在表1中。表1中的第一热源是亚冰晶石析出过程中产生的结晶潜热。对CR=3.0的NaF-AlF3二元体系，因未有过剩AlF3，不存在亚冰晶石结晶潜热，放热时间为0；对CR=2.7的体系，热分析实验测定的放热时间为5 s；对CR=2.4 的体系，实验测定的放热时间为15 s。表1中的第二热源是冰晶石立方结构向单斜结构转换时释放出的相变潜热，实验测定的平均放热时间为10 s。

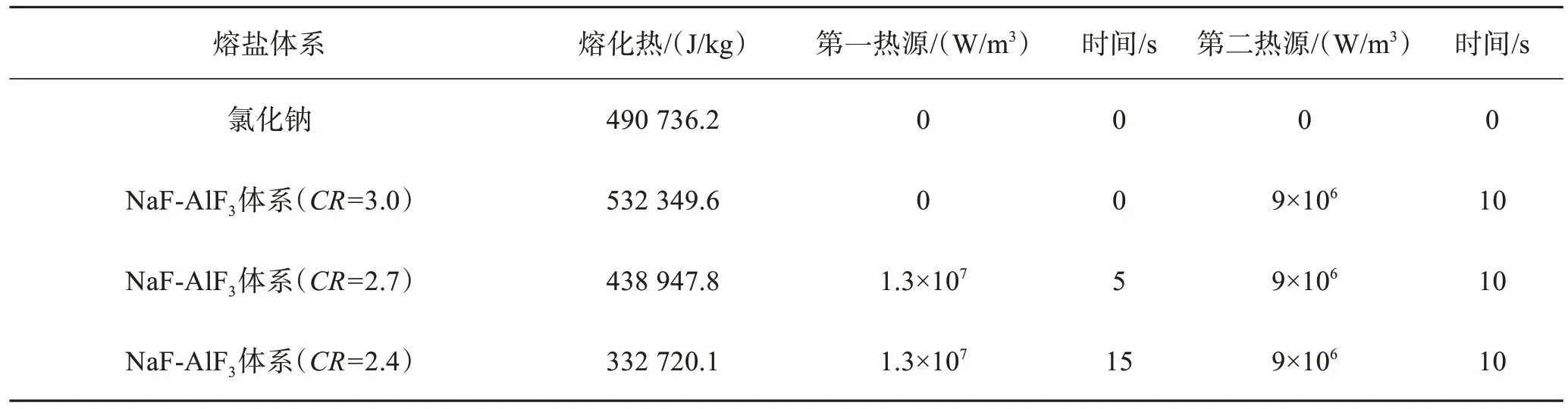
表1 模型中采用的热源S数据［24］Table 1 Data of heat source S adopted in the model［24］

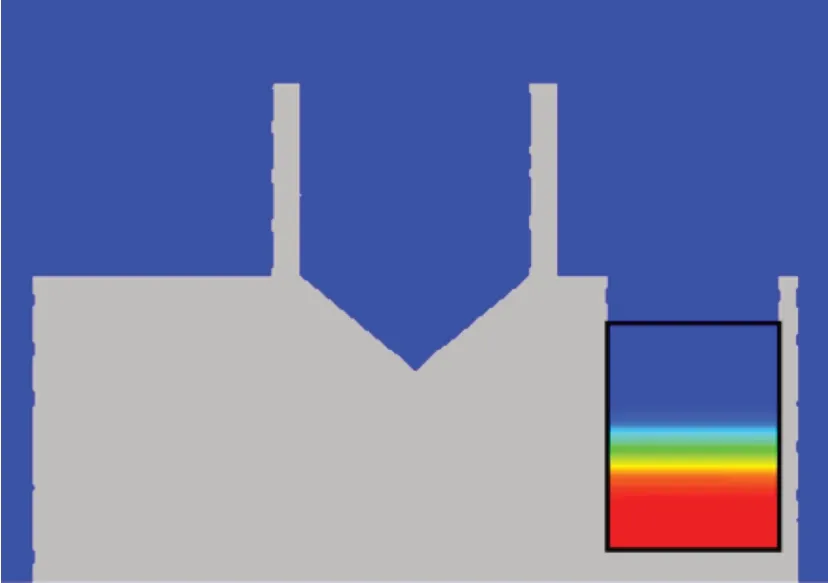
图4 模型中熔盐热源S区域Fig.4 Dominating area of heat source S of molten salt in sensor model

VOF多相流模型将其中一种流体q的体积分数记为αq，式（2）中的能量E的质量平均数则由式（3）计算；DO模型方向矢量s→的辐射传输方程则被视作场方程式（4）。

式（3）、式（4）中：αq为q流体的体积分数为位置矢量为方向矢量为散射方向矢量；a为吸收系数；n为折射率；σs为散射系数；σ为玻尔兹曼常数；I为辐射强度；ϕ为相函数；Ω'为固体角。

本文模型中所使用参比物[25]（304不锈钢）和熔盐[26-27]的密度和比热容等物性数据来源于文献。热导率与温度之间通常成反比关系，因此采用式（5）的形式来表述固定组成熔盐热导率与温度的关系。式（5）中m的取值与体系中的结晶相种类有关；X与体系原子的摩尔体积相关，因此该值的大小通常与温度相关，但为了简化，在一定温度范围内将其设定为常数。

在氯化钠体系中X1和X2分别代表熔融态和结晶态热导率K与温度1/Tm之间的系数；NaF-AlF3体系中X1、X2、X3则分别代表了液相线温度点以上、液相线温度点与563 ℃（836 K）之间以及563 ℃（836 K）以下温度段热导率K与温度1/Tm之间的3种比例系数。通过调整热导率方程式（5）的X值和m值，获得相应熔盐体系热导率的输入值，输入到流体计算模型中。

1.3 模型参数合理化

氯化钠熔盐常用作标准物质来校正物理化学性质测量系统的误差，因为可以得到高纯度的低成本试剂，同时在测试过程中性质稳定，相关的物理化学数据很完善。本文采用氯化钠熔盐来构建热分析有限元模型，将氯化钠熔盐在不同状态下的热导率数据作为标准值输入到模型中，通过调整模型的其他变量（诸如不锈钢材料的发射率和取点位置等）来构建能够有效拟合实验数据的有限元分析模型。

在传感器热分析实验中，不锈钢探头会在第一次使用后发生氧化，其表面发射率与崭新的探头有显著差别，并会对测试结果和模拟结果产生显著影响。如图5所示，这种影响仅限于第1次测试，后续的测量结果都展示出高重现性，因此实验数据通常采用最后几次测量结果。

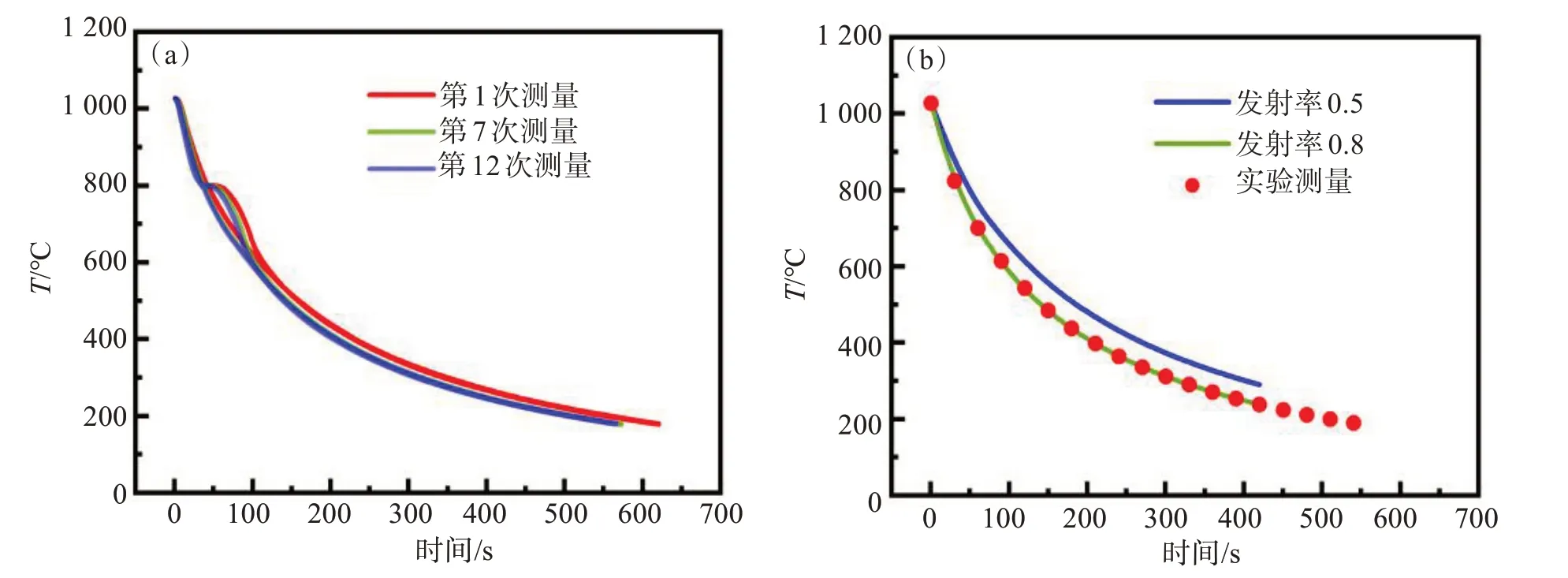
图5 不锈钢材料发射率对模拟结果的影响：（a） 多次测量的热分析实验数据；（b） 不同发射率的模拟结果对比Fig.5 Effect of emissivity of stainless steel on simulation results：（a） experimental data on multiple thermal analyses;（b） comparison of simulation results with varying levels of emissivity

在有限元分析模拟过程中，密度、比热容和热导率不变的条件下，经氧化的传感器探头发射率最小约0.5，最大约0.8[25]。当发射率设定为0.8时，模拟结果最接近于稳定后的实验结果。在参比物的降温曲线稳定的基础上，熔盐与参比物由于热物性不同引起的温度差异，则更容易通过实验和模拟的方法类比来获得不同状态的熔盐的热物性数据。

在读取有限元分析模型的计算结果中，分别在熔体区域和不锈钢柱体区域内部选取3个取样点进行对比分析。取样点位置见图6中的“+”标注位置。熔体中的3个位置分别标注为A、B、C；不锈钢柱体中的3个取样点的位置分别标注为A'、B'、C'，其中B与B'点位置是探头中热电偶测量端的位置。在这些点读取的温度数据对比如图7所示。可以看出B点和B'点的氯化钠降温曲线最接近实验数据，因此确定了模拟数据导出的取样点位置为B与B’。

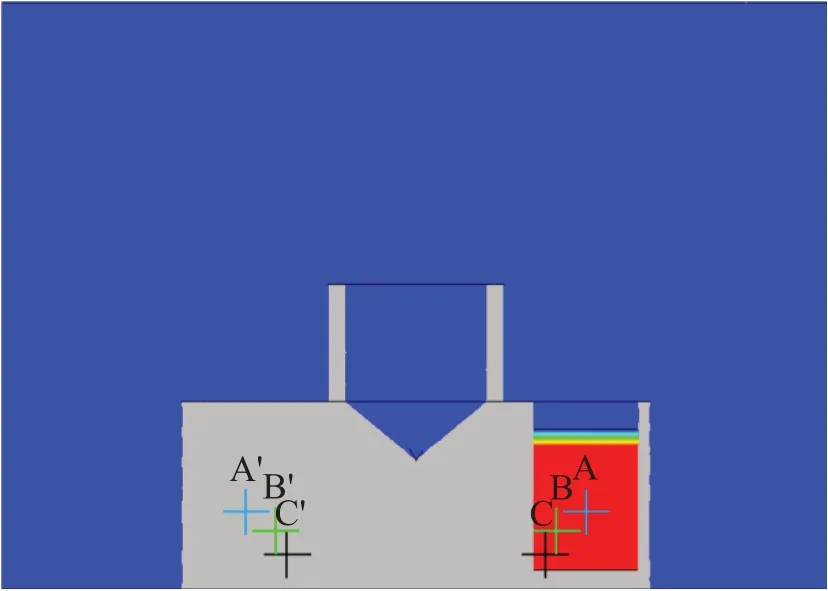
图6 模型中温度取样点的位置Fig.6 Temperature sampling locations in the model

图7 模型数据读取中温度取样点A/A'、B/B'、C/C'的降温曲线对比Fig.7 Comparison of cooling curves sampled at points A/A'，B/B' and C/C' in reading results of the model

传感器采集了1 127～277 ℃（1 400～550 K）的降温实验曲线，熔盐（氯化钠）和参比物（304不锈钢）的降温曲线在图8（a）分别用黑色和红色标出。对于单组元氯化钠体系而言，指数m=1。依据XU等[27]得出的热导率数据，计算得出的X1、X2分别为1 600和635。模拟计算得到的降温曲线在图8（a）分别用蓝色（氯化钠熔体）和绿色（参比）标出。

在上述条件下，模拟计算结果与热分析实验数据对比，氯化钠和参比温度的Pearson相关系数都达到0.999。残差峰值主要集中在90 s附近，最大不超过5%。如果获得的温度变化模拟值与实测的温度曲线的相对误差不超过5%，则认为热导率方程中的系数X和指数m有效。

2 结果与讨论

2.1 NaF-AlF3体系的热导率

基于氯化钠熔盐建立的有限元模型被用于研究NaF-AlF3二元熔盐体系的热导率。模拟中m的取值为2/3。该体系中分子比为3.0冰晶石的热导率已经被广泛研究，本方法得到的热导率数据与文献数据进行对比，可以用来评估这种方法是否可用于研究二元熔盐体系的热导率。

与氯化钠熔盐的热行为不同的是，CR=3.0的冰晶石熔盐在冷却过程中的热行为可分成3段，在563 ℃（836 K）附近还存在一个结晶潜热，因此式（2）中需要增加一个热源项，其数值对应表1中的第二热源项。

当式（5）中的X1、X2、X3分别取95、100、95时，通过模拟计算获得的降温曲线与传感器测量得到的数据的最大相对误差为2.58%，如图9所示。NaF-AlF3体系中分子比为3.0的熔盐在各个温度段的热导率可用式（6）—式（8）来计算：

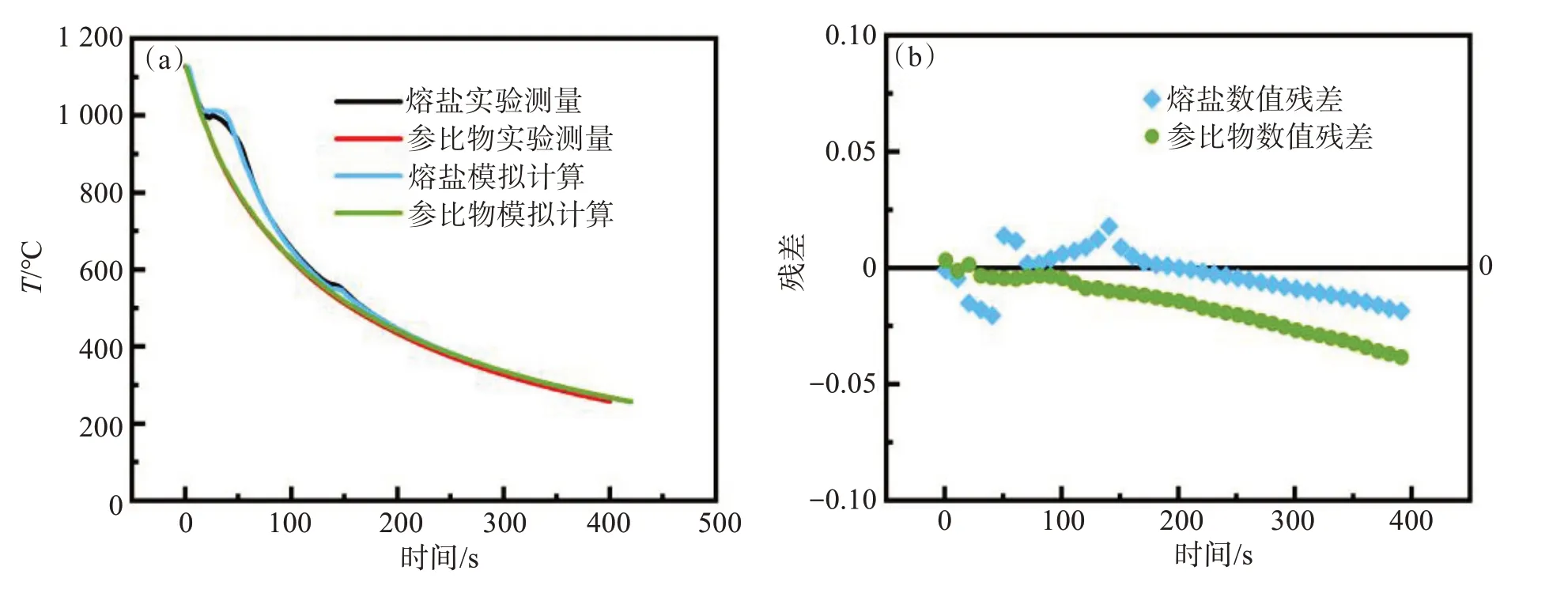
图9 NaF-AlF3熔盐（CR=3.0）热分析实验数据与模拟数据:（a）温度趋势；（b）残差Fig.9 Comparison of modeling data and experimental data for NaF-AlF3 system with CR=3.0：（a） temperature profile of cooling; （b） residual graph

将式（6）—式（8）计算所得到的热导率数据与文献[16]（红色）、文献[18]（深蓝色）、文献[15]（天蓝色）、文献[28]的单斜晶型（粉色）和立方晶型（黄色）模拟数据和实验测量数据进行对比，结果见图10，本方法得到的热导率（图10中曲线）与文献中的实验数据十分接近。在563～1 009 ℃（836～1 282 K）温度段，本方法得到的热导率计算结果优于EMD法，同时也证明这种传感器热分析与有限元分析相结合的方法，对研究存在多晶型转变的二元熔盐体系也有效。

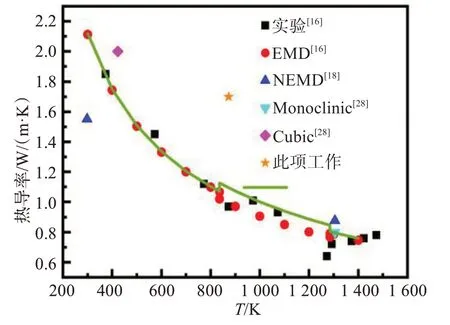
图10 NaF-AlF3体系（CR=3.0）冰晶石的热导率数据与文献数据对比Fig.10 Data comparison of thermal conductivities obtained in this work with literatures for the NaF-AlF3 system （CR= 3.0）

相比CR=3.0的冰晶石熔盐，分子比分别为2.7和2.4的热分析曲线中，在700 ℃（973 K）附近出现了新的放热峰，这对应于生成亚冰晶石的包晶反应，因此方程式（2）中的外源项需要增加亚冰晶石的结晶潜热，其数值对应表2中的第一热源项。

当X1、X2、X3分别取90、93、93时，模拟计算获得的CR=2.7熔盐的降温曲线与实验测定值的最大相对误差为2.7 %，如图11所示。

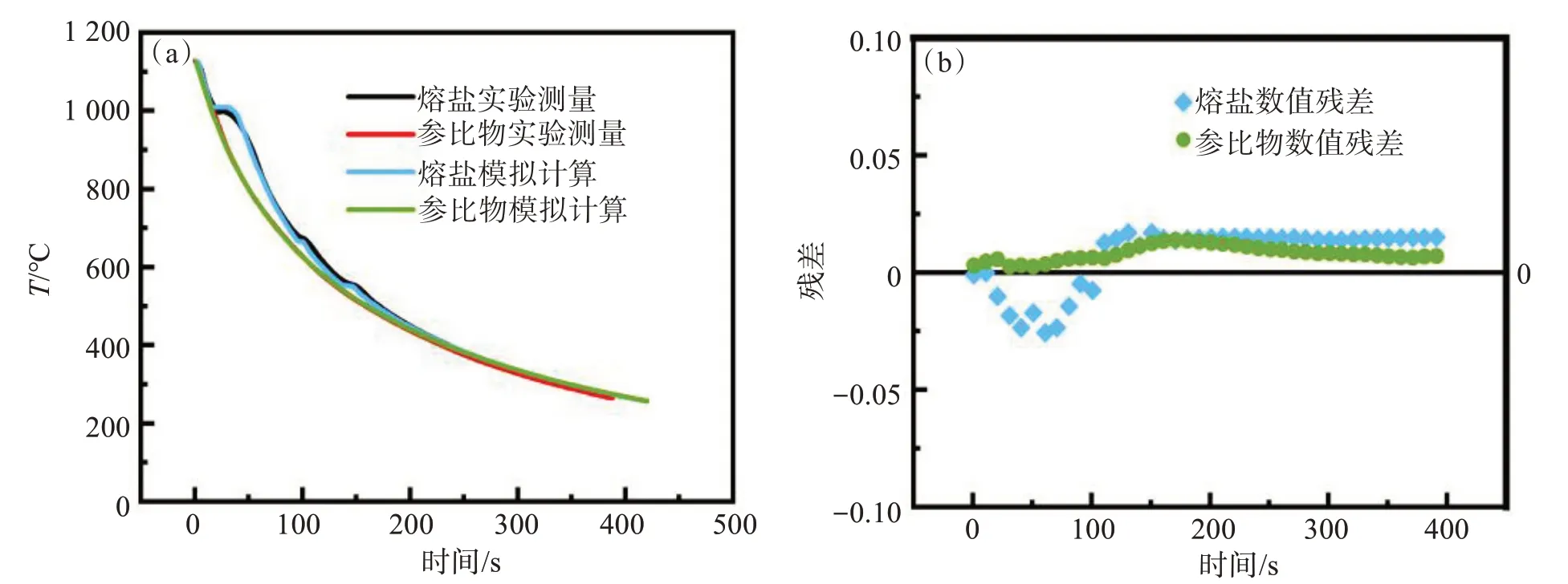
图11 NaF-AlF3体系（CR=2.7）实验数据与模拟数据对比：（a）温度趋势；（b）残差Fig.11 Comparisons of modeling data with experimental data for NaF-AlF3 system with CR=2.7：（a） temperature profile of cooling; （b） residual graph

当X1、X2、X3分别取80、85、90时，模拟计算获得的CR=2.4熔盐的降温曲线与实验测定值的最大相对误差为3.28 %，如图12所示。

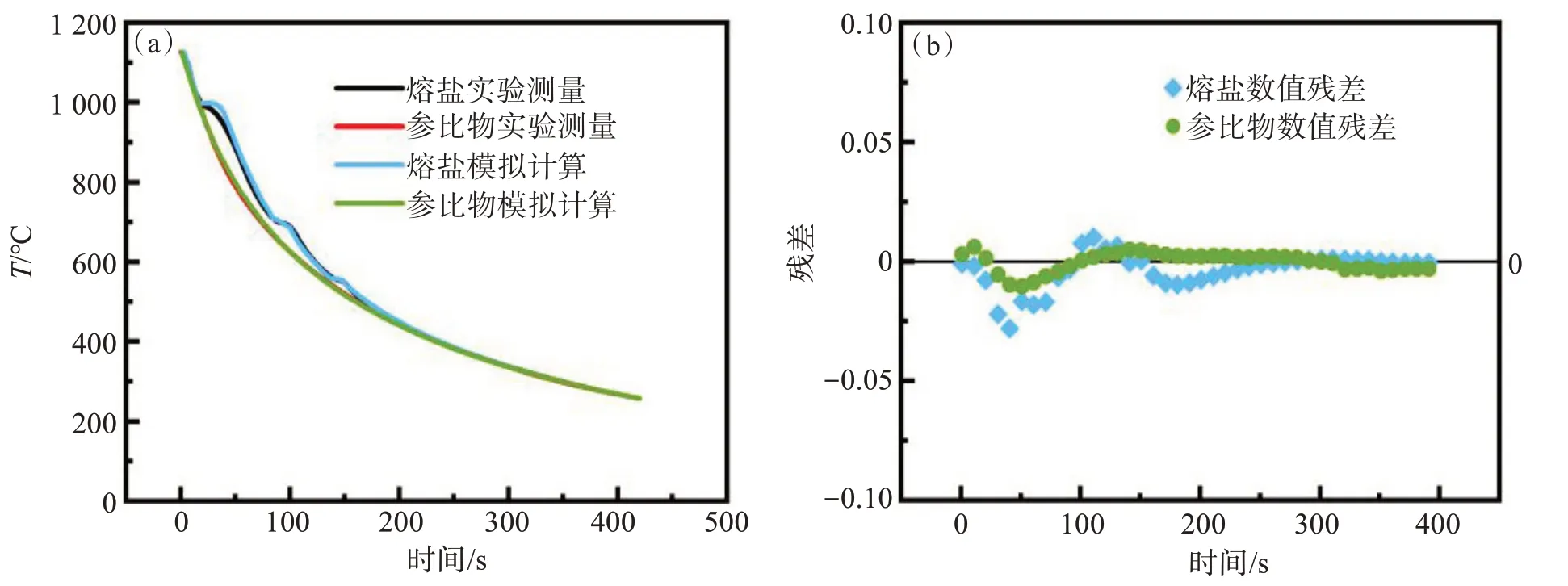
图12 NaF-AlF3体系（CR=2.4）实验数据与模拟数据对比：（a） 温度趋势；（b） 残差Fig.12 Comparisons of modeling data with experimental data for NaF-AlF3 system with CR=2.4：（a） temperature profile of cooling; （b） residual graph

图13对比了3种分子比的冰晶石熔盐的热导率结果，可以看出低于563 ℃（836 K）的完全固相温度段，分子比越高，固态熔盐的热导率越大。工业上的实践证明，铝电解质的分子比越高，固相电解质的密度越大，质地也越致密，其导热性也越好，即热导率越高，这与本文中得到的规律相一致。CHERⅠBⅠ等[16]基于分子动力学和密度泛函方法模拟了不同类型冰晶石的热导率。研究结果表明，亚冰晶石（Na5Al3F14）热导率低于冰晶石（Na3AlF6）热导率。因此，分子比降低，NaF-AlF3体系中亚冰晶石相（Na5Al3F14）的含量增加，热导率下降。与本文的规律是一致的。

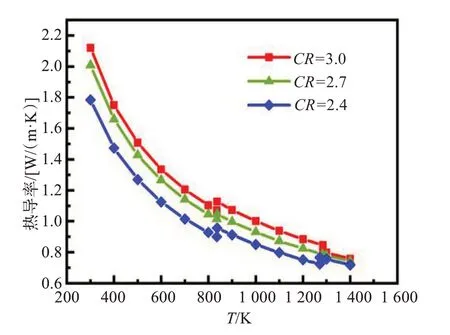
图13 不同分子比的NaF-AlF3体系热导率的对比Fig.13 Comparison of thermal conductivities of NaF-AlF3 at various cryolite ratios

KHOKHLOV等[15]测量了不同分子比的液态NaF-AlF3体系的热导率，其测试结果表明，体系的热导率随分子比下降而降低，与本文的规律一致。在1 000 ℃（1 273 K）, 分子比分别为3.0、2.7和2.4组成的热导率分别为0.791、0.774、0.755 W/（m·K）。本文的结果分别为0.809、0.792、0.766 W/（m·K），与文献[15]中的结果非常接近。

2.2 NaF-AlF3体系热导率与分子比的关系

构建NaF-AlF3体系热导率与分子比和温度的关系式更有实用价值，可以更方便地用于铝电解槽的热场分析中。基于理论计算，CR分别为3.0、2.7和2.4的NaF-AlF3固相体系中亚冰晶石的含量分别为0、17.56%和37.51%。建立各温度段X常数与亚冰晶石含量的关系图，并作线性拟合，如图14所示。X1、X2和X3都与亚冰晶石的质量分数之间存在线性关系，尤其后两者的线性相关系数超过0.99。因此，X常数可用体系中的亚冰晶石含量（ω%，质量分数）线性表达，见式（9）—式（11）所示。

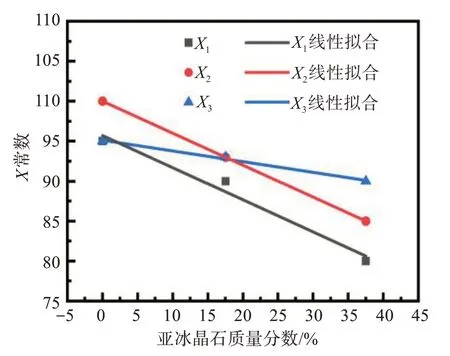
图14 NaF-AlF3体系中亚冰晶石的质量分数与X系数之间的关系Fig.14 Relationship between X and mass fraction of Chiolite in NaF-AlF3 system

基于亚冰晶石质量分数与CR之间的关系，将X系数与CR建立起联系，然后与式（5）相结合，最终建立NaF-AlF3体系的分段热导率方程，如式（12）—式（14）所示：

3 结论

1）本文将热分析传感器与有限元分析结合起来，开发研究了一种确定熔盐热导率的新方法，研究结果表明，该方法不但可以用来研究单组元熔盐的热导率，也可以用来研究双组元熔盐的热导率。

2）利用这种新方法，本文研究了NaF-AlF3体系的固态热导率和熔融态热导率，建立了NaF-AlF3体系的分段热导率方程，可用于计算该体系随分子比变化和温度变化的热导率，计算结果与文献数据吻合良好。