埋地燃气PE 管道在地面沉降作用下的应力分析

宋晓娟 彭星煜 豆旭昭 王金波 梁香娜 邵艳波

（1.中国石油工程建设有限公司华北分公司，河北任丘 062550；2.西南石油大学石油与天然气工程学院，四川成都610500；）

0 引言

据统计，我国埋地管道由于地面沉降而发生管道泄漏等事故高达0.5 ～0.6 次/a。特别是北方地区冻土融化后地面较松软，一定程度的载荷将致使地面发生沉降，导致埋地管道产生大变形而失效，因此管道的安全问题就显得格外重要。当地面发生沉降时，土体会直接作用于管道上并造成挤压，致使管线发生大变形而遭到破坏。因此地面沉降是导致管道破坏的重要因素之一。目前我国大部分城镇燃气管道采用聚乙烯材质，且管网错综复杂，受到的外载荷工况也多种多样，如占压、积压、穿越、沉降等，本文选取影响最为显著的地面沉降工况对管道受力特性进行研究，为埋地燃气PE管道的安全评估提供理论参考。

目前针对典型复杂工况下的埋地管道响应分析研究方法主要有试验方法、理论解析法和有限元分析法。试验法可直观反映管土模型的真实受力情况，也可直接观测管道的破坏过程及破坏模式；是目前接受度最高的方法之一；但缺点是试验周期长，时间成本过高。理论解析法主要通过对管道受力进行分析，在已有的力学基础上通过简化假设形成相应的数学模型对管土受力情况进行分析计算；随着有限元软件的日益成熟，有限元方法逐渐被广泛应用于各种复杂工况下管道的响应研究，且认可度也越来越高。

ZHENG J Y 等［1］通过有限元软件，提出了埋地管道的最大主应变强度破坏准则，拟合出地面沉降的位移分布式。LUO X 等［2］借助ABAQUS 有限元软件讨论了地面沉降区域的大小对管道屈服的影响。马小明等［3］通过对站内埋地钢管进行测试，采用ANSYS 有限元分析软件搭建了土体-管道非线性接触模型，并与实际测量值对比得到更为准确的有限元模型，并探讨了管径、管道埋深、土体弹性模量等参数对管道应力响应的影响；石磊等［4］采用ANSYS 对谐波沉降作用下含内压钢管的受力情况进行数值模拟。刘威等［5］采用ABAQUS 有限元软件分析了不同材质的埋地管道的抗沉降能力，为不同地质条件下埋地管道材质的选择提供了参考。

本文采用ANSYS软件进行模拟计算，通过分析PE 管道在地面不同程度的沉降作用下的PE 管道的应力应变响应情况，来得出PE 管道的受力规律、管道失效机理和失效原因及失效影响因素。

1 管土模型建立

1.1 模型基本假设

埋地管道在地面沉降作用下一般会受到多种荷载作用，其中影响较大的是管道内压与土体对管道造成的压力。

根据文献［1］，ZHENG J Y等采用电磁感应法检测埋地管道的失效段对实际地面沉降规律进行测量，发现地面沉降分布接近四次多项式曲线。如图1 所示。

图1 地面沉降区域实际测量值和四次多项式拟合曲线对比

地面实际沉降具有复杂性，为了便于计算，确保模型的准确性，且不受外界环境影响，需对模型进行合理简化：①假设管道只有管体本身，无任何管件；②土体模型是均匀各向同性的材料；③沉降分布呈四次多项式曲线；④忽略PE 材料的蠕变和松弛特性；⑤为了更好研究管道受力规律，本文管体模型选用粘弹性模型。

1.2 材料性能与参数

根据文献［6］所提及的，地面沉降作用可视作准静态加载，其沉降速率大约为20 ～70 cm/a，本文取地面沉降速率为40 cm/a 来估算管道的应变率，PE管应变率计算方法如下：

管道变形后的弧长公式：

则管道应变率为：

式中，x为最大沉降位移m；s为沉降后的管体真实长度，m；l为管道原长，m；L为沉降半径，m；t为应变时间，s。

由上述方程可得：当地面以40 cm/a的速率沉降时，聚乙烯管的应变率约为0.000 1 s-1。

根据文献［7］，取得PE管道的参数如表1 所示。

表1 PE 管道材料参数

目前对于管土力学研究的模型应用较为广泛的有 Mohr-Coulumb 弹塑性模型（M-C 模型）和Drucker-Prager 模型（D-P 模型）。M-C 模型的计算结果较为保守，D-P 模型相对比较稳定，多用于管道的大变形计算，且在冲击载荷下可以很好地展现材料的弹塑性状态，更能反映出管道的应变情况［8］。因此本文的土体模型选取D-P 模型。土体D-P 模型参数见表2，土体D-P 模型的硬化参数见表3。

表2 土体D-P 模型参数

表3 土体D-P 模型的硬化参数

1.3 模型尺寸

根据《PE 燃气管道工程技术规程》（CJJ63—2023）［9］以及文献［10］，管道埋深取0.9 m。

在该算例中，沉降区L1=10 m，由于地面沉降的两侧非沉降区具有对称性，为了便于计算，本文只设置单侧非沉降区，取沉降区长度的1/2 作为非沉降区来进行考虑，即L2=5 m。则有限元模型长（L）×宽（W）×高（H）=15 m×3 m×2 m，如图2 所示。

图2 模型边界条件

聚乙烯材质选取PE100，公称直径DN=110 mm，公称壁厚e=10 mm。

网格划分采用多区法（Multizone），整体单元设为6 面体8 节点实体单元，平均Jacobian Ratio（MAPDL）=1.094 9，符合计算要求。如图3 所示。

图3 有限元分析模型

1.4 边界条件

ANSYS软件的solution模块可以分为边界条件设置以及载荷加载等步骤，本文主要分为三步来进行分析。

（1）初始分析步。埋地管道受到的外部载荷较复杂，本次计算中，主要考虑的载荷为管道内压0.35MPa、重力9 800mm/s2以及土体沉降对管道作用，由于模型具有对称性，且固定端面不受土体沉降作用影响。因此本次计算在固定端面上施加了fixed support位移约束。其余土体面与管道两端采用对称约束。

（2）接触分析步。接触问题属于边界非线性问题，在PE管道的泊松效应下，当管道受到载荷时会发生一定程度的变形，即接触面会随着外载荷的变化而变化。管土接触分析对模型的计算至关重要，需要考虑以下几个问题：①管土接触面定义。有限元软件中的接触方式有面—面接触、点—点接触和点—面接触，本模型的接触主要为管道外表面与土体的接触，为面—面接触。②接触判别。本文将管土交界面处的管线外表面定义为刚性目标面，将目标面对应的土体表面定义为接触面［11-12］。③管土摩擦模型选择。本文选取Frictional 接触，管道与土体之间的摩擦系数取0.4［13-14］。④设置接触初始穿透值为0。

（3）加载分析步。由2.1 章节得到沉降区的沉降曲线为四次多项式曲线，如式（3）所示：

式中，y、z分别为Y、Z的坐标值，mm；m、n为常数；c为最大沉降位移的取值，mm；L是受沉降区的管道长度。

沉降区L=10 000 mm，设最大沉降位移为：c=0 mm、c=100 mm、c=180 mm、c=280 mm、c=400 mm、c=1 000 mm，根据x（0）=0，x（L）=0，可导出m、n数值，位移加载如图4 所示。

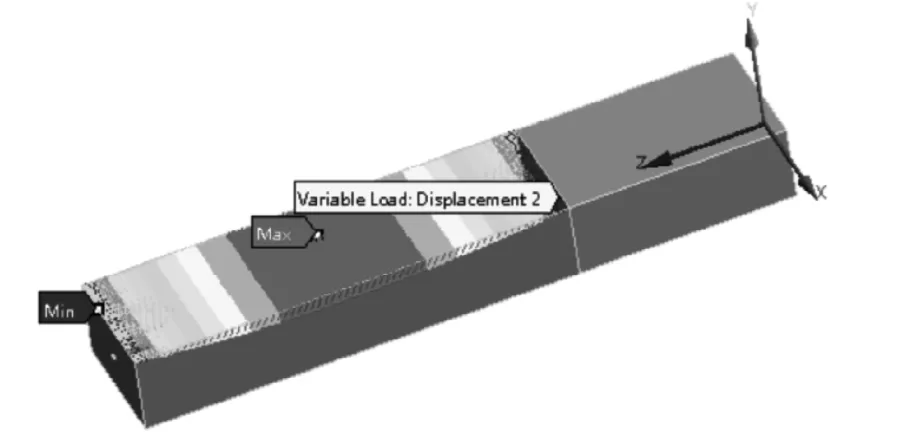
图4 根据四次多项式加载的位移载荷

2 管道有限元分析结果

2.1 应力分析

以管道最大沉降量180 mm为例，如图5 是地面以40 cm/a沉降速率作用下的速率下沉到180 mm时PE 管道应力云图。对于管道截面应力分布，其最大Von-Mises 应力出现在沉降段与非沉降区的交界处管道下端外表面。

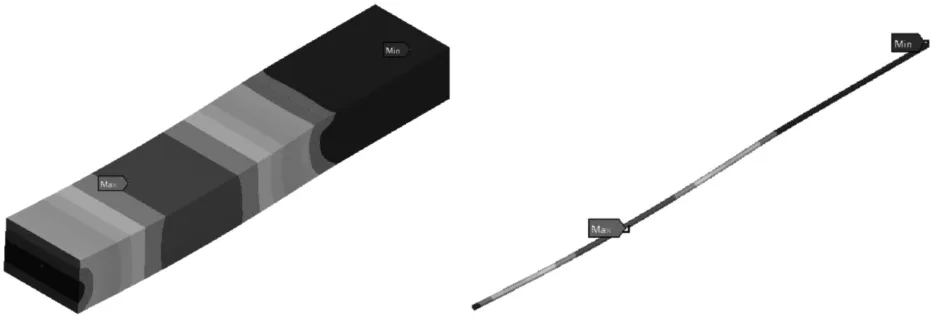
图5 地面沉降量c=0.18 m 时埋地PE 管道应力云图

观察图5、图6，当最大沉降位移c=180 mm 时，PE 管的应力为7.916 9 MPa，其最大Von-mises 应力出现在沉降段与非沉降区交界处管道下端外表面。文献［6］对城镇用SRD=11 的PE100 燃气管道进行蠕变实验获得PE 燃气管道的本构模型，在以40 cm/a沉降速率作用下的屈服强度为15.19 MPa，因此当管道沉降位移为180 mm 时，管道并未达到屈服值，可以安全运行。

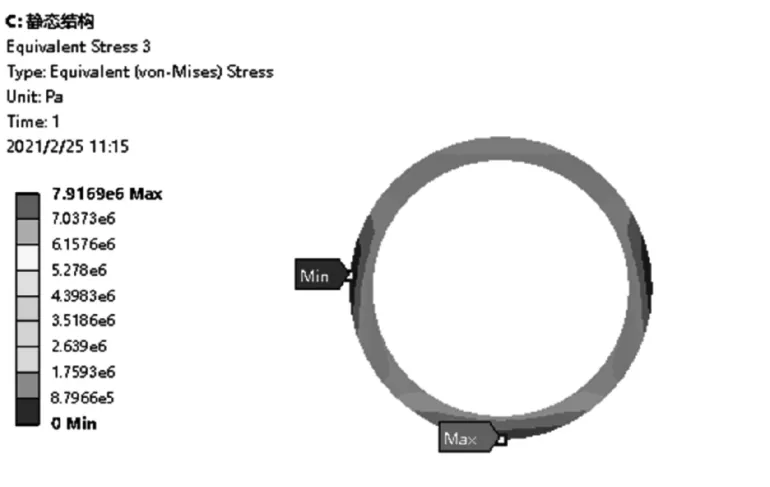
图6 管道横截面应力

2.2 应变分析

PE 管道在外力或自重作用下会产生弯曲变形，弯曲变形一般用曲率半径描述，曲率半径越小，说明PE 管道的弯曲程度越剧烈。最小曲率半径可表征管道抗弯曲能力。

当管道受到挤压时，会产生压缩变形。压缩变形越大，PE 管道截面就越扁，管道椭圆化越严重。压缩变形由管截面变化率表示［15］，其计算式（4）如下：

式中，为管道横截面椭圆变化率；d0为管道的实际外径，mm；d0′为椭圆化后管道的短外径，mm。

图7 为在最大沉降位移为180 mm 时的PE 管道轴向弯曲变形，由图可知，非沉降端与沉降端的交界处附近管道弯曲变形最严重，为9 560 mm，其次管道沉降最大位移处的管道弯曲变形也较严重，由于管道两侧的应力响应互不影响，因此导致模型的固定端与非沉降端的应变波谷不同，由于沉降具有对称性，因此本文忽略固定端一侧的应力应变情况，只对沉降区域的一半模型进行研究。

图7 最大沉降量为0.18 m 时管体沿轴向曲率半径

图8 给出了管道沿轴向的截面椭圆变化率的分布情况，由图可知PE管的最大截面变化率为0.171，出现在沉降区与非沉降区的交界处。

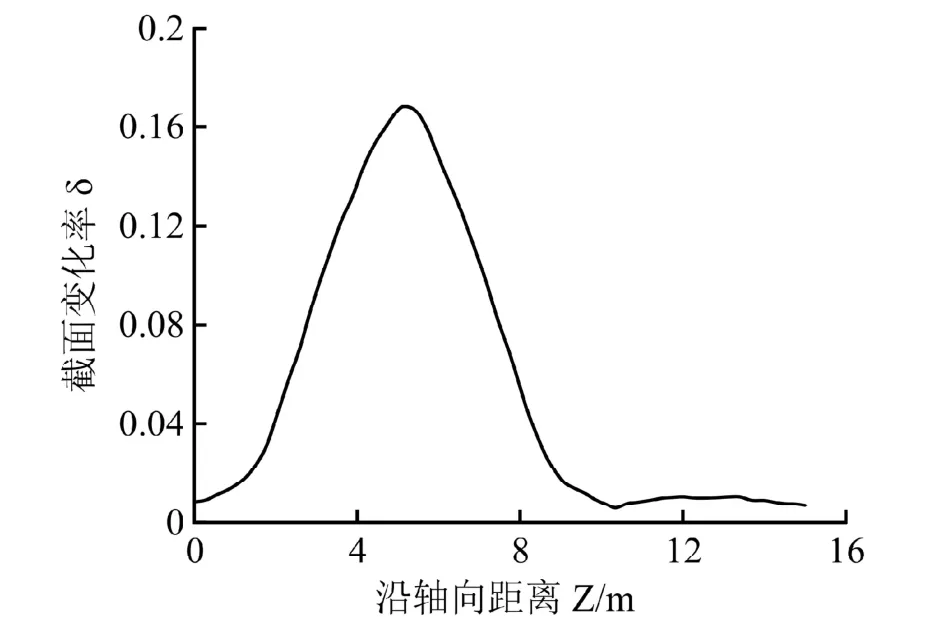
图8 最大沉降量为0.18 m 时管体沿轴向截面变化率

3 不同沉降位移对PE 燃气管道的影响

不同沉降量下的PE 管道应力云图见图9，PE燃气管道最大Von-mises 应力随最大沉降量变化曲线见图10。

图9 不同沉降量下的PE 管道应力云图

图10 PE 燃气管道最大Von-mises 应力随最大沉降量变化曲线

由图9 可知，不论管道的沉降量为多少，可以比较明显地发现管道的最大等效应力总是出现在沉降区与非沉降区交界处管道上。由图10 可看出在沉降区域为10 m 时，管道的最大应力与地面最大沉降位移近似线性关系。可得出在地面沉降作用下PE100、DN110 的管道可承受的极限位移载荷为280 mm。由于本文选用的PE管道本模型为弹性模型，因此管道的受力情况不受屈服强度的影响，管道失效后等效应力仍然会增大。

图11 给出了当沉降区域为10 m 时，随地面最大沉降不同，PE 燃气管道的最小曲率半径和最大椭圆截面率变化情况。由图可知随着沉降位移的增加，管道的最大截面变化率呈增大趋势，最小曲率半径呈减小趋势。且当沉降位移达到极限值时，管道的最大截面变化率为0.197，最小曲率半径为8.04 m。

图11 PE 管道应变随最大沉降量变化曲线

3.1 管道环向应力分析

随着沉降量的增加，管道的最大应力逐渐由管道下端表面转移至左右两侧表面。由于左右两侧为受力对称的两侧，为了更好描述管道的受力情况，本文将对称截面的起拱线的6 个位置分别定义管顶上表面A，管顶下表面B，管底上表面C，管底下表面D，管道侧外表面E，管道侧内表面F，如图12 所示。

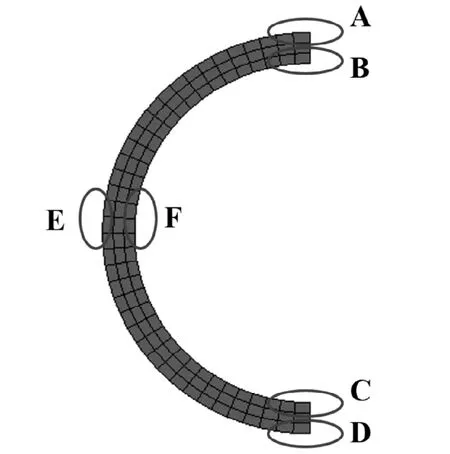
图12 PE 管对称横截面上的位置

在这6 个潜在危险点中，A 点与D 点主要受到管道弯曲变形造成的拉应力，B 点与C 点是压应力；E点受到土体对管道挤压产生的拉应力，F点则是压应力。

图13、图14 为随着地面沉降量的增大，A、B、C、D、E、F这6 个点的应力变化图以及最大应力随沉降位移变化图。

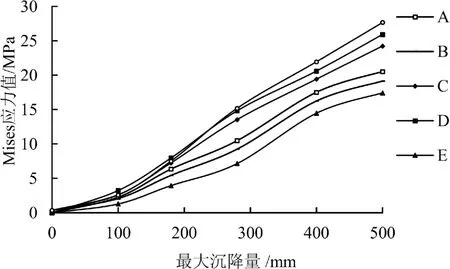
图13 6 个潜在危险点的应力随着最大沉降位移变化

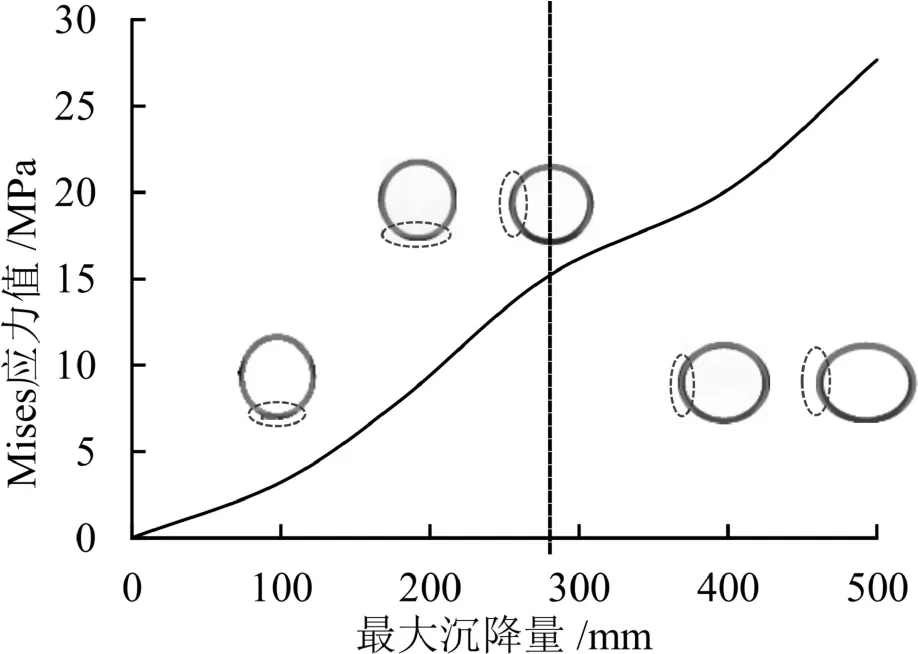
图14 最大Von-Mises 应力随沉降位移变化

由图13、14可知，当最大沉降量在100～180 mm时，管道的最大应力出现在管道底部D点处，应力由3.66 MPa 上升至7.9 MPa，最大应力增幅较小，当沉降位移为180 ～280 mm时，此时F点的应力急速上升，管道最大应力逐渐由D 点转移至F 点，当最大沉降量达到280 mm时F点应力管道达到屈服值15.19 MPa。

由图14 可知，当管道达到屈服值后，管道的横截面已经被压缩变形并椭圆化。出现应力转移的原因是：随着沉降位移的增大，管道受到土体的错位挤压更为明显，使得轴向弯曲变形更为严重，管道轴向弯曲变形继而引起管道截面的椭圆化严重，导致管道内侧F 点受到的压应力急剧上升，此时管道的最大应力主要影响因素已从管线的弯曲变形转为自身的压缩变形。因此本文将管道内侧表面F 点定义为管道失效的危险点。

3.2 管道轴向应力分析

由于每种沉降量沿管道轴向Z 的应力分布都较为相似，本文选取沉降量0.18 m为例，绘制管道位置点A—F 点沿管道轴向位置（Z 轴）的分布情况，如图15 所示。

图15 6 个危险潜在点沿轴向距离应力变化

由图15 可知，应力最大的地方分布在管道沉降区与固定去的交界处，出现这种现象的原因是在管道沉降区与固定去出现了载荷突变，使得管体上出现应力集中。

管道上端与管道下端应力明显偏大，但管道侧端相对应力较小，这是由于当沉降量较小时，管道主要受到来自上端土体的压力，管道侧端受力主要是由于管道弯曲造成的压应力所导致，管道本身变形量不大，因此管道压缩变形不严重，但是相较于拉应力而言其压应力更小，几乎对管道侧端无影响。

观察图15 可发现，各位置点的应力峰值是向过渡段两端存在偏移，且偏移位置随着沉降量的增大越发明显。出现这一现象的主要原因是：在地面沉降作用下，土体塌陷对管道造成的挤压作用导致管道产生变形，土体变形与管道变形并不是同步产生，因此在挤压过程中管道会在Z 轴方向产生滑移，导致应力峰值位置发生偏移和滞后。

为了探究压缩作用与弯曲作用对PE 管道失效的影响，本文单独对PE管道的抗压缩能力与抗弯曲能力进行模拟计算。设置在管道处于极限位移状态下：①只设置管道的极限曲率半径值R=8.04 m；②只设置PE管道承受的极限压缩作用，使其截面变化率为=0.197。

结果表明：在只有弯曲作用下，当PE 管道的最小弯曲曲率半径为8.04 m 时，管体的最大等效应力为10.21 MPa；在只受到压缩作用下，当PE管道的最大截面变化率为0.197 时，管体的最大等效应力为14.82 MPa，均未达到屈服值。由此可以得出：地面沉降作用下，管道的受力具有复杂性，土壤沉降引起管道轴向弯曲变形，管道轴向弯曲变形继而引起管道截面的椭圆化压缩变形严重导致管道失效，因此管道失效是由管道的弯曲变形与压缩变形综合作用导致的，但压缩变形占据主导作用。同时也很好解释了随着沉降量的增加，管道的最大等效应力从管道底部D 点转移至危险点F 点这一现象。也可得出管体弯曲变形的存在会加速管道失效。而沉降区域的增大可增大管道的曲率半径［5］，减小管道的弯曲变形，进而使得管道的压缩变形也得到一定减小。因此材质为PE100、管径DN110、e=10 的燃气聚乙烯管道在地面沉降作用下能承受的最大截面变化率为0.197。

4 结论

本文借助ANSYS 软件，对材质为PE100 的聚乙烯管道在沉降区域为10 m 时的受力情况进行有限元分析，主要得出以下结论：

（1）在地面沉降作用下，管道在沉降区域的边界应力响应最大，管道的弯曲变形与压缩变形在沉降区域边界也最为严重，且随着沉降量增大，管道会在轴向上产生滑移现象。

（2）当沉降量较小时，沉降区域边界管道底端的应力响应相较于其他部位较大；随着沉降量的增加，管道内侧F 点的应力急剧上升，为管道的失效危险点。因此在实际工程中应避免在此范围内设置管件、接头等强度相对较低的设施。

（3）在地面沉降作用下，压缩作用在PE 管道的失效中占主导作用，且管道弯曲变形的存在会加速管道失效。因此尽量避免埋地燃气管道在存在压缩变形的同时也产生弯曲变形；也可通过增大沉降区域半径减小管道的弯曲变形，从而减缓管道的压缩变形，增加管道承受极限位移的能力，为埋地燃气管线的维抢修争取更多的响应时间。