基于优化灰色理论的高可靠性产品寿命预测
沈 杰, 李云飞
(西华师范大学 数学与信息学院, 四川 南充 637002)
0 引言
在实际的工程问题中,采用正常的寿命试验预测高可靠性产品的寿命往往需要很长的时间.目前,国内外学者针对该问题,采用加速寿命试验的数据分析与评估技术能有效预测高可靠性产品的寿命,并建立了诸多加速模型[1].但由于在电子、航空航天等领域的高可靠性产品价格昂贵且寿命长,所以即使是加速寿命试验所得到的失效数据也相对较少.因此,如何在短时间内得到较多的失效数据,以及由少量数据建立更准确有效的加速寿命模型,从而预测在正常环境下的产品寿命成了高可靠性产品的可靠性研究重点之一.
19世纪80年代Arrhenius提出了描述产品寿命与温度应力之间关系的Arrhenius模型[1],并广泛应用于加速寿命试验的寿命预测中.邓聚龙教授于20世纪80年代初创立了灰色系统理论,主要为了解决“少数据、不确定性”系统的分析预测、决策与控制问题[2].由于加速寿命试验中得到的失效数据少,产品寿命难以确定,因此,近年来,灰色理论被广泛应用在产品的寿命预测中[3-8],其中GM(1,1)预测模型是灰色预测技术的基本模型,其研究与应用十分广泛,一直受到国内外关注[9-13].Liu等[3]以温度为加速应力,建立了基于Wiener过程和GM(1,1)模型的故障寿命预测模型,对RCD(residual current device)在正常使用环境下的剩余寿命进行了推算.Cai等[4]提出了一种优化的等维动态NEGM (1,1)模型,采用等维动态预测算法预测船舶CXF型电缆的寿命.Zhang等[5]提出了一种基于GM(1,N)模型的寿命预测方法,用于定量评估XLPE电缆的老化程度,并确定其剩余寿命.Gai等[6]通过对原始数据的对数变换,对数据进行累积,建立GM(1,1)模型并对特征寿命进行分析预测.彭琦允等[7]提出了基于灰色系统理论的气体激光器寿命试验数据预测算法和寿命预测模型,缩短了试验时间,提高了寿命预测精度.钱毅等[8]采用传统均值生成背景值的灰色预测模型,结合等维灰数递补和信息模型对加速预测模型进行了修正.蒋玉婷等[9]采用几何法构造背景值的灰色预测模型对加速寿命试验数据进行了预测分析,对传统Arrhenius加速模型的参数进行了一定的修正.
综上,以上学者都是利用灰色预测模型直接对寿命进行预测,忽略了加速模型对寿命预测本身的重要性.本文则提出一种基于背景值优化的灰色预测模型的修正方法,将灰色预测理论与加速模型相结合,对服从指数分布Exp(1/θ)场合下的恒加寿命试验数据进行分析.主要利用优化的灰色预测模型将产品的失效数据进行有效等维扩充,并对比优化灰色模型与传统模型的拟合误差,再用扩充后的新数据对加速模型参数进行修正,对比检验加速模型的显著性,最后采用修正后的加速模型对产品进行寿命预测,对比检验模型的相对误差和预测精度.
1 灰色预测模型GM(1,1)[2]
设原始寿命序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),其中,x(0)(k)≥0(k=1,2,…,n),称x(1)=(x(1)(1),x(1)(2),…,x(1)(n))为序列x(0)的一次累加生成序列(1-AGO),其中
(1)
称Z(1)为X(1)的紧邻均值生成序列,其中
(2)
则称
x(0)(k)+az(1)(k)=b
(3)
(4)
得到GM(1,1)模型的最终还原式[2]为:
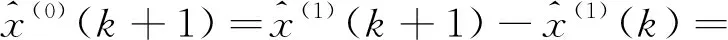
(5)
2 灰色预测模型GM(1,1)的优化
2.1 动态寻优法构造灰色背景值
传统GM(1,1)模型中的背景值是模型预测误差的主要原因之一.由式(5)可以发现,GM(1,1)模型的预测值与发展系数a、灰色作用量b有关,即模型预测精度与a、b的取值有关,而背景值z(1)(k)的构造会影响a与b的取值,因此可以通过改变背景值的构造方式来提高模型的预测精度.因此本文将背景值构造公式中的固定值1/2变为动态变量α,然后采用动态寻优法寻找α,根据试验数据找到使平均相对误差MRE(mean relative error)最小的变量值,从而对GM(1,1)模型进行优化,使模型的预测精度提高.平均相对误差的表达式为:
(6)
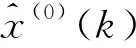
Z(1)(k)=αx(1)(k)+(1-α)x(1)(k-1),k=2,3,…,n,
(7)
其中权重α满足0≤α≤1.

(x(1)(k)-x(1)(k-1))+a(αx(1)(k)+
(1-α)x(1)(k-1))=b,
其一阶线性方程形式为:
(8)
则a,b的估计值可由以下式子得到:
其中
设上式计算结果为(c1,c2)T,解方程组可得:
a=(c1-1)/(α-αc1-1),b=(-c2)/(α-αc1-1),
(9)
将a,b的估计值代入式(3)和(5)中即可得到时间响应式及还原值.
2.2 灰色预测模型的精度检验

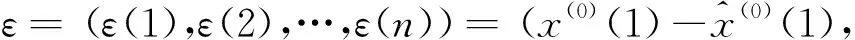
(10)
且有
(11)


表1 灰色预测模型精度检验等级
3 定时截尾样本下的统计分析
3.1 定时截尾样本下的可靠性统计分析

(12)
其中,
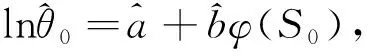
3.2 加速模型的显著性检验
考虑用相关系数检验法来检验这个加速模型的显著性[14].一组配对样本
(xi,yi)=(φ(Si),lnθi),i=1,2,…,k,
它们的相关系数定义为:
(13)
其中,
对于给定的显著性水平α(0<α<1),从表2[14]中在自由度f=k-2栏下查得临界值rα.若|r|>rα,则认为这个样本xi与yi相关,这时可认为加速模型可用于预测,且相关系数越高,显著性越高,预测效果更好.

表2 相关系数检验临界值
4 算例分析
已知某电子产品的寿命服从指数分布Exp(1/θ),所选的4个加速温度水平分别是70 ℃,90 ℃,110 ℃和130 ℃.从同类产品得知,此电子器件在30 ℃到150 ℃的失效机理相同,只是其平均寿命(h)不同而已.在这里采用恒加定时截尾的试验方法,试验数据如表3[14]所示.接下来,首先将传统GM(1,1)模型与优化GM(1,1)模型进行拟合误差检验,通过对比表明优化GM(1,1)模型的拟合精度更高,拟合数据更贴近原始试验数据,因此可用优化模型对失效数据进行等维扩充,得到50 ℃,70 ℃,90 ℃,110 ℃和130 ℃下新的失效数据,再利用新数据对加速模型进行参数修正.用新的寿命失效数据对加速模型的显著性进行检验,通过计算表明利用新数据得到的加速模型的显著性更高,最后分别通过传统加速模型和修正加速模型对70 ℃,90 ℃,110 ℃、130 ℃下的寿命进行预测,并对比预测精度.

表3 恒定温度加速寿命试验数据
4.1 传统GM(1,1)模型与优化GM(1,1)模型模拟结果
4.1.1 利用传统GM(1,1)模型模拟
将加速温度分别为130 ℃,110 ℃,90 ℃,70 ℃下的平均寿命对数lnθi(0)作为原始序列:X(0)=(4.018 2,5.030 4,5.754 4,6.743 9),应用式(1)-(5)对原始数据进行分析,得到响应式的参数:a=-0.147 4,b=4.041 9,从而得到响应函数为:
4.3088×e0.1474k,k=1,2,…,n.
4.1.2 利用优化GM(1,1)模型模拟
根据原始寿命序列采用动态寻优法,使平均相对误差(MRE)达到最小值,根据式(6)-(9),得到MRE的最小值min(MRE) =0.003 606(见图1),此时α=0.48作为最优背景值.通过计算得到响应式的参数:a=-0.147 9,b=4.053 9,从而得到响应模型为:
k=1,2,…,n.

图1 平均相对误差(MRE)
4.1.3 模型的精度对比
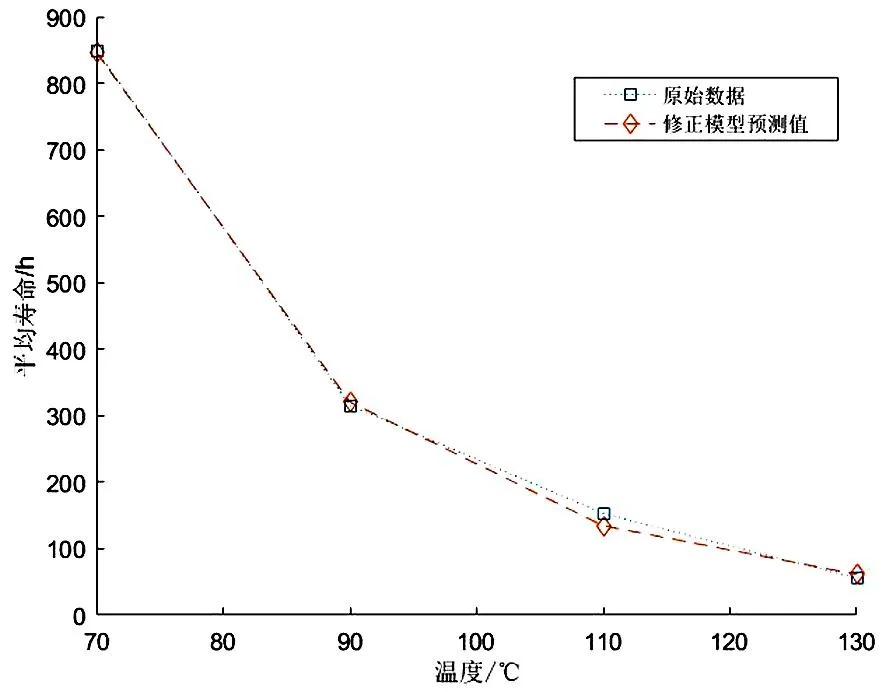
根据式(10)-(11)可以得到GM(1,1)模型的均方差比值C1=0.046 86和小误差概率p=1>0.95,优化GM(1,1)模型的均方差比值C2=0.046 80和小误差概率p=1>0.95,查表1为一级精度(好).并且此时有:C2 4.1.4 模型的模拟误差对比 模拟寿命与原始寿命的相对误差(绝对值): 模拟寿命与原始寿命的平均相对误差: 则有误差表分别如表4和表5所示 表4 GM(1,1)模型误差 表5 优化GM(1,1)模型误差 通过表4和表5也可以发现:优化GM(1,1)模型比传统GM(1,1)模型的拟合平均相对误差更小,寿命更符合产品规律.且在低温70 ℃下的相对误差更低:1.01<3.81,证明在越接近产品正常使用的低温情况下,优化GM(1,1)模型的预测精度越高.但由于灰色预测模型的个别相对误差偏大,平均相对误差较大,不适合直接用于寿命预测.因此,以此模型进行失效数据扩充,再结合加速寿命模型进行寿命预测. 4.2.1 修正模型与传统模型的显著性对比 4.2.2 传统加速模型与修正模型的建立 4.2.3 修正模型与传统加速模型的预测误差对比 利用传统Arrhenius加速模型预测加速应力130 ℃、110 ℃、90 ℃、70 ℃下的平均寿命分别为:(60.60 h,134.20 h,324.40 h,869.12 h).利用Arrhenius修正模型预测加速应力130 ℃、110 ℃、90 ℃、70 ℃下的平均寿命分别为:(61.42 h,134.39 h,320.52 h,845.95 h).则有误差表分别如表6和表7所示. 表6 传统Arrhenius加速模型误差 表7 Arrhenius修正模型误差 通过表6和表7可以发现:修正模型比传统加速模型的相对误差和平均相对误差更小,且在70 ℃下的相对误差远低于传统模型:0.35%<2.38%,精度提高约85.29%,说明在越接近产品正常温度的情况下,修正模型的预测精度越高.这是因为利用优化GM(1,1)预测模型得到了更精确的50 ℃下的寿命,使原始寿命数据得到了有效的等维扩充,利用扩充数据所建立加速模型,提高了模型预测的显著性和准确性.可得其拟合数据与原始数据的拟合曲线如图2所示. 从图2也可以看出,修正后的加速模型所得到的预测值与原始值接近程度很高,表明优化灰色预测理论对加速模型的修正的确具有很好的效果. 图2 修正模型预测值与原始值 本文研究了在加速寿命试验中,根据少量的失效数据如何有效建立加速模型,对正常温度下高可靠性产品的寿命预测问题,可得如下结论. (1)在加速温度跨度和间隔越大的情况下传统加速模型的预测偏差越大,只要失效机理相同,可建立等维灰色预测模型,得到其他温度下更多的失效数据,建立显著性更高的加速模型. (2)经优化灰色预测模型扩充的失效数据,根据原始数据与拟合数据之间的相对误差判断,扩充数据既符合产品寿命规律,又能有效提高加速模型的显著性.运用此方法进行寿命扩充,既不用考虑特定的寿命分布,与计算机算法需要大量的训练数据相比,更具适用性,且不会产生不良数据,预测得到的失效数据更贴近真实数据. (3)基于优化灰色预测模型的方法能有效修正加速模型的参数,提高了加速模型的预测精度,与只运用灰色预测模型进行寿命预测相比,既减少了预测的平均相对误差,又将灰色预测模型与寿命预测中的经典加速模型进行结合,使寿命预测的结果更加可靠和信服,而且此方法在只有少量失效数据的情况下也具有很好的预测效果.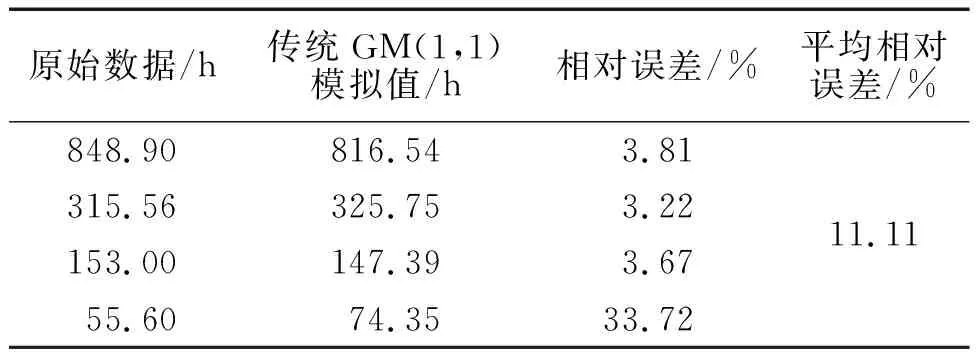

4.2 Arrhenius修正模型与传统Arrhenius加速模型预测结果
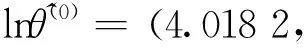
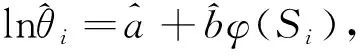
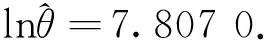


5 结论

