黏土中的孔压测试试验及其传递滞后机理

唐逸凡,曹小为,李 明,崔 灿,宋林辉

(1.南京工业大学 数理科学学院,南京 211800; 2.徐州地铁集团有限公司,江苏 徐州 221000 )

0 引 言

饱和黏土中的孔压传递过程是岩土工程的核心问题之一,涉及土坝渗流与地下结构抗浮等诸多工程问题。理论上,对处于封闭状态的饱和土体而言,考虑到常规压力下水的不可压缩性,施加的水压在土体中是瞬间传递的。

具体而言,如果依据弹性力学理论,饱和土体中的孔隙水压力传递速度接近15 km/s[1],也有学者指出承压含水层中的孔压传递接近声速[2]。但在工程实测中发现饱和黏土中的孔压传递并不是瞬时完成,而存在明显的滞后现象。

国外,Richards等[3]、Bennett等[4]和Okusa等[5]在观测海底土体中的孔压时发现,海浪、暴风雨等荷载作用下的孔压在海底土体中传递会出现明显滞后;Raynaud等[6]在分析高岭土的渗透性时发现渗透过程中孔压传递很缓慢;Abdollahi等[7]分析海啸形成的波浪荷载作用下土体内孔压的响应也有明显滞后。国内,唐益群等[8]发现地铁振动荷载下隧道周围饱和软黏土的孔压发展缓慢,相关固结和渗流试验也表明黏土中的孔压传递具有滞后性质[9-10]。至于饱和黏土中孔压传递滞后的原因,主要定性地归纳为3类:一是测试仪器造成的[11],二是土体或水中含有的气体压缩引起的[12],三是因水压作用下弱结合水作剪切运动、强结合水会发生变形,由此产生的传递阻力导致了滞后[13]。

为了明确饱和黏土中孔压传递过程,并验证前述孔压传递滞后原因的定性猜测,本文开展黏土孔压传递过程测试试验,对不同固结压力下的饱和黏土施加水压,量测土体不同位置处的孔压变化,以分析其传递过程;在此基础上,采用有限元软件对试验进行数值仿真,定量探讨土体渗透性和孔隙水压缩性对孔压传递过程的影响。

1 试验方案

1.1 试验土体

试验用土取自某基坑坑底,将其晾干、粉碎、过1 mm筛后,进行常规土工试验,得到土体的颗分曲线如图1所示,粒径含量和物理参数分别如表1和表2所示。

表1 土体粒径含量

表2 土体物理参数

图1 土体的颗分曲线

由上述参数可以判断试验土体为低液限的级配不良黏土。

1.2 试验装置

试验装置包括孔压测试筒、固结压力施加杠杆、水压施加设备和数据采集系统,其中的孔压测试筒是关键部件,如图2所示,由不锈钢底座、亚克力筒和不锈钢顶板组成,三者相互之间采用橡胶垫和螺栓连接,可装配形成密闭腔体。

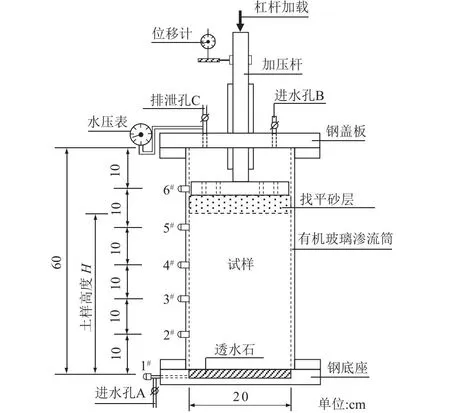
图2 孔压测试筒

钢底座侧边留有带测压孔的进水孔A,以便从底部施加确定的水压。筒体总高60 cm、内径20 cm,筒体侧壁沿高度方向每隔10 cm均匀设置了5个测压孔(孔内设有透水石),测压孔通过细管与孔压传感器相连,并利用电脑自动采集数据。钢盖板中间设有加压杆套,加压杆通过杆套穿过盖板传递杠杆荷载给试样施加固结压力,加压杆上加装有小平板用于放置位移计;盖板上另设2个孔道,一个是进水孔B,用于试验前的注水;另一个是带水压表的排泄孔C,用来排气排水,2个进水孔和1个排泄孔均设有阀门,可按需开启和关闭。

水压由气泵经密闭罐施加,如图3所示,密闭罐带气囊,将内部空间分成气室和水室,其中气室的进气口接气泵,水室的出水口接渗流筒钢底座上的进水孔A,气泵加压后,气室的压力传递到水室实现加压,且可避免气体混入水中。

图3 水压加载装置

1.3 试验加载方案

为便于对比,一共进行2组试验,试验加载方案如表3所示。

表3 试验加载方案

由表3可见,两组试验(T1和T2)均是在施加初始固结压力pc0和初始水压pw0的基础上,按初始水压20%的幅度施加增量水压,并观测孔压变化。

1.4 试验步骤

每组试验可细分为以下8个步骤。

(1)准备工作:组装试验装置并进行密封性检测,确保试验过程中不漏水。同时将粉碎过1 mm筛后的黏土放入饱和桶中抽气饱和,时长≥24 h。

(2)界面防渗处理:在渗流筒内壁涂抹一层凡士林,其中接孔压计的孔口处及往上5 cm区域在抹凡士林前贴上1 cm宽的胶带、抹好凡士林后再撕掉,这样既可避免筒壁与土体界面间的渗漏,又能避免凡士林堵住孔口。

(3)土体填筑:将饱和好的黏土分5层填入渗流筒内,并打开侧壁的测压孔和底座的进水孔A,静置10 h以上,以使土体在自重下排水固结。

(4)施加初始固结压力:在筒内土层上部填入厚约5 cm用于找平的砂层,通过杠杆逐级施加荷载直至达到表3中每组试验所要求的固结压力,且在该固结压力下土体的沉降稳定,即变形<0.01 mm/h。

(5)常规土工试验:卸下加压杠杆,在土样顶部用环刀取样,进行常规土工试验,表4为每组土样的物理力学参数,同时对环刀取样后的土样表面进行修整刮平,确保土样满足试验高度。

表4 土样的物理力学参数

(6) 施加初始水压:用注满水的水管将筒壁测压孔与孔压传感器连接、进水孔B与水桶连接,然后从排泄孔C中抽气,水在负压下流入筒上部,且可保证无气泡,注满后关闭排泄孔和进水孔B。

再由进水孔A从试样底部施加初始水压,静置5 d,装置照片如图4所示。

图4 试验装置照片

(7)施加增量水压:开启数据采集系统,采集每组试验中各测点的初始孔压,并设置数据采集间隔为3 min,然后按表3施加增量水压,直至各测点孔压达到稳定状态,稳定状态的判断标准是每小时孔压变化值小于该组试验初始水压的0.1%(即<0.1%pw0/h),且每组试验的时间≥48 h。

(8)数据处理与分析:运用采集的数据对比各测点的孔压及其变化规律。

(9)试样土工试验:将渗流筒内的土样取出,沿高度方向从上至下依次分4层取环刀试样,进行常规土工试验,然后取平均值,可得到试验后土样的物理参数,如表5所示。

表5 试验后的土体物理参数

对比表4和表5可知,土样在试验前后的物理参数基本一致。

2 试验结果

依据试验步骤(1)—步骤(5),可完成试样的制作,并得到初始孔压,如表6所示。再依据试验步骤(6),施加增量水压,并量测筒侧各点孔压,可得到各测点的孔压变化,如图5所示。

表6 试验初始孔压

图5 施加增量水压后各测点孔压随时间的变化

由图5可见,1#测点的水压瞬间增加到设定大小,位于试样中的2#—5#四个测点的孔压变化响应按序由先往后,与水压施加点1#位置的距离远近密切相关,表明增加的孔压在黏土中传递需要时间,存在滞后现象。6#测点基本与5#测点变化同步,因为6#测点位于水中,孔压传递很快。

2#—6#测点的孔压变化都经历了由陡增到缓变、再到稳定的过程,依据前述<0.1%pw0/h的孔压稳定标准,可得到各点孔压达到稳定状态时的时长,即孔压传递滞后时长,并与试验结束时各点的孔压一起列于表7。

表7 孔压传递滞后时长及试验结束时的孔压

由表7可知,试样的孔压传递滞后时长随固结压力的增加而增大,表明固结压力越大,土体越密实,渗透系数越小,孔压传递所需的时间就越长。

3 孔压滞后的数值仿真分析

3.1 数学模型

在实际的饱和黏土渗流过程中,孔隙水压力的变化会引起土骨架有效应力变化,导致土骨架以及黏土颗粒的变形,从而引起黏土渗透系数、孔隙率等特性发生改变,同时,这些特性的改变又会影响到孔隙水的流动与压力的传递。将试验黏土视作多孔弹性介质,考虑以上因素的流固耦合方程为

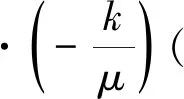
(1)

式中:k、φ分别为黏土试样的渗透率与孔隙率;μ为水的动力黏度;pw为孔隙水压力;ρw为水、气两相的混合密度(以下简称水的密度);g为重力加速度;Es、Ew分别为黏土和水的压缩模量;εv为土骨架的体积应变;Qm为流体源汇项。

其中,水的压缩模量Ew与水的压缩系数c互为倒数,即

(2)

忽略温度场的影响,并认为黏土颗粒不可变形,由于孔隙水压力的变化(Δpw)引起的土骨架变形从而导致的孔隙率变化为

(3)

而由孔隙水压力变化导致的渗透率变化为

式中k0、φ0分别为黏土试样的初始渗透率与初始孔隙率,均由试验获得。

依据弹性力学与饱和土体有效应力原理,得出试验土体中的应力张量σij表达式为

σij=2Gεij+λδijδklεkl-φδijpw。

(5)

式中:G为剪切模量,G=(1-2v)Es/(2-2v);λ为拉梅常数,λ=vEs/(1-v);v为泊松比;εij、εkl为应变分量;δij、δkl为Kronecker数。

由弹性力学可知应变和位移的关系为

(6)

式中ui,j、uj,i为位移梯度张量。

由此可知体积应变与位移的关系为

(7)

根据静力平衡条件可知

∇·σ+Fv=0 。

(8)

将式(5)、式(6)代入式(8)得到包含孔隙水压力修正项的应力平衡方程为

Gui,jj+(G+λ)uj,ji-φδijp,i+Fi=0 。

(9)

式中:ui,jj、uj,ji(i,j=x、y、z)为i,j方向上的位移;p,i为孔隙水压力;Fi为i方向上的体积力。

联立式(1)与式(9)可得

式(10)即为渗流-应力场耦合方程,在进行渗流应力耦合模拟前,对试样施加相应的先期固结压力,将此固结压力下试样中的应力作为第二类皮奥拉-基尔霍夫应力(Piola-Kirchoff Stress)以外部应力张量的方式加载到耦合场中,以建立渗流应力场耦合的数学模型。

3.2 数值模型及验证

试样为圆柱体,直径20 cm,高度分别为45 cm(T1试样)和44 cm(T2试样),现采用有限元软件Comsol Multiphysics建模,选用二维轴对称单元,模拟区域是沿圆柱体径向和中心轴截开的长方形区域,如图6所示。

图6 模拟区域示意图

边界条件设置分为固体力学与流体力学两部分,如图7所示,6#测点位于土体上部纯水部分,这一部分的孔压传递介质为纯流体,几乎不存在滞后现象,为提高计算稳定性,不设置6#测点,仅考虑土体部分的渗流应力耦合。

图7 边界条件设置

数值模拟的部分计算参数通过常规土工试验获得,如表8所示。根据式(2)可知,此时孔隙水的压缩系数为4.5×10-7kPa-1。

表8 数值模拟参数

为验证数值模型的合理性,按图7所示的边界条件以及表8所示的参数对前述试验进行数值模拟,模拟编号分别为S0-1和S0-2,并将模拟结果与试验数据进行对比,如图8所示。

图8 模拟结果与试验数据对比

由图8可见,模拟工况下各测点的孔压增长趋势与试验相同,呈现先陡增后进入稳定的趋势,不过,除1#施加水压处外,其余4点孔压在陡增阶段的吻合度较差,总体的增长幅度均偏小,这是由于在增量水压施加过程中,水压力有打开流道的作用,土样中会形成少量优势流道,这些流道降低了土样的渗透性,而数学模型中渗透率变化(式(4))不能描述该过程。因此,数值模拟中的土样渗透性较试验更小,从而导致施加增量水压后出现孔压初始增长阶段滞后于试验实测的现象,且固结压力越大,土样渗透性越弱,滞后越明显,不过,最终稳定阶段的孔压值基本吻合。依据前述<0.1%pw0/h的孔压稳定标准,可得到数值模型的孔压传递滞后时长,并与模拟结束时各测点的孔压一起列于表9。

对比表9与表7可见,各点孔压模拟计算值的滞后时长偏少于半小时内。另外,两组数值模型的1#—5#测点最终孔压值与实测值非常接近,差异率最大仅为1.27%,表明该模型可以较好地模拟试验过程,验证了数值模型的合理性。

3.3 孔压传递滞后分析

尽管试验前对土样进行了充分振捣, 但孔隙水中仍会混有气体, 现将气体与孔隙水作为整体, 通过改变孔隙水的压缩系数来探讨流体压缩性对孔压传递滞后的影响。 流体压缩系数有多种定义方式[14], 本文采用式(11)描述孔隙水密度与压缩系数的关系。

ρw=1 000×exp[c(pw-p0)] 。

(11)

式中:c为孔隙水压缩系数(Pa-1);p0为大气压,取0.1 MPa。

为验证孔隙水的压缩性对孔压传递滞后的影响,针对T1和T2试验,制定S1和S2数值模拟方案,每项模拟均选取6个水压缩系数;另外,为分析土体渗透系数对孔压传递过程的影响,基于T1试验,制定S3数值模拟方案,同样变化6个土体渗透系数,具体如表10所示。

在进行S1和S2模拟时,其他参数取自表8且保持不变;同理,在进行S3模拟时,令孔隙水压缩系数为0,其他参数也取自表8且保持不变。

通过S1和S2的模拟,可得到2种固结压力下(200和300 kPa)试样中的孔压传递滞后时长随孔隙水压缩系数变化的定量关系,以散点形式绘于半对数坐标系中,如图9所示。

图9 孔压传递滞后时长随孔隙水压缩系数的变化

由图9可见,当孔隙水压缩系数在10-8～10-6kPa-1之间变化时,孔压传递滞后时长基本不变;一旦>10-6kPa-1后,随着孔隙水压缩系数的增加,滞后时长缓慢增长;达到10-5kPa-1后,滞后时长开始大幅上升。整个变化过程可采用单指数函数进行拟合(见图9)。

研究表明,含气饱和水的压缩系数一般在10-7kPa-1左右,并随着土体中气体含量的增加,压缩系数可迅速增大到10-4kPa-1左右[15]。结合图9可知,气体含量较少时,孔隙水连通,土体中的气泡多以离散封闭形式存在,水压增量可以在连通的孔隙水中迅速传递,少量的离散封闭气泡对传递过程几乎没有影响[16],因此,图9中,当c<10-6kPa-1时,孔压传递基本不受孔隙水压缩系数的影响。当气体含量继续增加,土体中离散的气泡逐渐连通,此时含气孔隙水整体表现出的可压缩性较大,附加水压力会挤压气泡,但因土体封闭,被挤压的气泡无法排出,在附加水压力的作用下这部分气泡的体积逐渐被压缩,缩减气泡体积形成的空隙将被后续渗入的孔隙水填补,因此,土体中具有压缩性的孔隙水渗流行为,本质上是气泡受水压力作用体积减少,后续孔隙水不断补充,填补空隙的过程,当气泡在附加水压力作用下体积不再减小或以缓慢的速度减小时,整体孔隙水压力呈现出稳定状态。显然,当土体中气体含量越多,孔隙水压缩系数越大,相同的水压力增量下,气体被压缩体积就越大,后续需要更多的孔隙水入渗补充,孔压传递滞后时长就越长,因此,当孔隙水压缩系数在10-6～10-5kPa-1之间变化时,土体中的气泡逐渐连成一片,并对孔压传递过程造成一定影响,图9中两条曲线均有小幅上升。当土体中的气泡连成一片,含气孔隙水压缩系数在10-5～10-3kPa-1变化,孔压传递滞后时长受孔隙水压缩系数的影响大幅提升,图9中的两条曲线均在该范围内急剧上升。

另外,对比图9中的S1和S2可知,土体固结压力越大,相同孔隙水压缩系数下,孔压传递滞后时长越长,而固结压力会显著影响土的渗透系数,对此,基于T1试验参数,令孔隙水压缩系数为0,依据表10中的S3模拟方案,进一步开展渗透系数对孔压传递滞后时长影响的分析。

图10为孔压传递滞后时长与渗透系数的半对数关系图。由图10可见,滞后时长随渗透系数增大而呈指数级减小,当渗透系数<10-9m/s时,孔压传递滞后时长受渗透系数的影响很大,随着渗透系数的增大,滞后时长降幅减小。当渗透系数增大到10-8m/s数量级后,滞后时长的下降速度变缓,并最终趋于0。

图10 孔压传递滞后时长随渗透系数的变化

由地下水动力学可知,渗透系数k受孔隙介质特性与流体特性的综合影响,即

(12)

由式(12)可知:k与孔隙介质的孔隙率n、平均孔隙直径的平方R2成正比,与平均弯曲度T成反比;同时,k还与孔隙水密度ρ成正比,与孔隙水动力黏度μ成反比。当孔隙水压缩系数为0时,密度ρ和动力黏度μ均保持不变,此时,渗透系数k的变化取决于孔隙介质的自身特性(n、R2、T),这也解释了图9中压缩系数不断向0逼近时孔压传递时长依然为一个非0常数的现象。结合图10可知,当孔隙介质自身特性变化时,比如从黏土到粉土再到粉砂变化时,渗透系数在不断增大,孔压传递滞后时长先是急剧下降,而后缓慢下降,最后趋于0(即瞬间传递完成)。

4 结 论

通过设计试验装置,对饱和黏土中的孔压传递过程开展测试试验,并运用数值仿真手段对孔压传递滞后的影响因素进行模拟分析,得到以下结论:

(1)测试结果表明饱和黏土中的孔压传递存在明显的滞后现象,且滞后时长与土体所受固结压力相关,固结压力越大,滞后时间越长。

(2)所建立的数值模型可结合试验模拟出孔压传递滞后的现象,并分析得到孔隙水压缩性和土体渗透性是饱和黏土孔压传递滞后的影响因素,其本质是孔隙水中的气体压缩使得孔隙水入渗补充形成渗透而导致滞后。

(3)基于数值模拟的参数分析发现孔压传递滞后时长随孔隙水压缩系数的增大而增加,尤其在压缩系数>10-5kPa-1后开始大幅上升;另外,孔压传递滞后时长随土体渗透系数的增大而减小,尤其当渗透系数>10-9m/s时,孔压传递滞后时长降幅急剧,达到粉砂的渗透系数级别后基本趋于0,孔压传递不再存在滞后。