改进移相控制下PMSG-PET系统回流功率的优化

谢子殿, 陈令猛, 焦文良

(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)

0 引 言

随着工业不断进步,对非线性和敏感性电力需求的急剧上升,给电网带来的各种问题层出不穷。各类负荷对电能的要求标准也在不断提高,导致电力系统中的电能质量问题受到关注。新能源发电[1]中电力电子变压器的投入使用能够解决电力系统中面临的诸多问题。

关金萍[2-3]提出了基于电力电子变压器接口的双馈感应电机风力发电系统,通过建模验证了风力发电系统采用电力电子变压器接口的可行性及系统的有效性。许志伟等[3]在Matlab/Simulink中模拟三级型电力电子变压器的输出电流来验证其不同的输出特性。林立等[5]分析了PMSG发电机侧系统的原理及建立了数学模型。笔者通过改进电力电子变压器中变换器的控制方法,以降低PMSG-PET系统回流功率。

1 电力电子变压器的结构及原理

电力电子变压器(PET)也称为固态变压器或智能变压器等。电力电子变压器具备电力电子变换与电能变换的能力。电力电子变压器可以通过控制原、副边的电压或者相位大小来调节电压、电流和功率。因此,通过将电力电子变压器应用于电力系统中能够解决回流功率等问题。

1.1 电力电子变压器结构

若不考虑高频变压器的AC/AC变换环节,将PET分为单级型、双级型和三级型[6-7]。根据隔离级DAB的不同结构,将PET拓扑分为四类[8-9]。文中所采用级联型电力电子变压器,如图1所示。

图1 级联型电力电子变压器结构 Fig. 1 Cascade type power electronic transformer structure

由H桥串联构成输入级,隔离级采用的是双有源桥DC/DC变换器,逆变级采用的是三相逆变器[10]。

1.2 电力电子变压器工作原理

电力电子变压器的工作原理[3]如图2所示。原边电力电子变换器将交流输入转换为高频交流,传输到高频变压器的原边,在高频变压器的副边感应出感应电动势,再通过PET副边变换出所需的工频交流输出。

图2 PET工作原理Fig. 2 PET working principle

2 PMSG风电系统建模

2.1 系统数学模型

PMSG-PET系统的简化等效电路如图3所示。PMSG-PET系统由级联型电力电子变压器及PMSG风力发电系统[11-15]构成,由图3分析级联型电力电子变压器组成部分的数学模型。

图3 PMSG-PET系统简化等效电路Fig. 3 Simplified equivalent circuit of MSG-PET system

2.2 电力电子变压器输入级

对级联H桥做出假设:忽略开关器件的损耗将其视为理想器件。因为输入级级联H桥每相采用同样的控制方式,a、b、c三相只需要建立其中一相的数学模型。以a相为例,建立方程为

式中:Ea——网侧交流电压;

Lm——网侧滤波电感;

VN——电容电压;

RN——输入阻抗。

通过建立电路微分方程可得a相的等效模型,如图4所示。

图4 H桥等效模型Fig. 4 H bridge equivalent model

b、c两相同理,得到等效模型为

假设H桥每相电压、电容、占空因数以及阻抗均相等,即

Vai=Vbi=Vci=VH,

Cai=Cbi=Cci=CH,

dai=dbi=dci=dH,

Rai=Rbi=Rci=RH,

式中:V——各相H桥电容电压;

C——各相直流侧支撑电容;

d——占空比;

R——负载。

将式(2)、(3)坐标变换到dq坐标系下表达式为

式中:Ed——坐标系d轴电压;

Eq——坐标系q轴电压;

id——坐标系q轴电流;

iq——坐标系q轴电流;

dHd——占空因数直轴分量;

dHq——占空因数交轴分量。

2.3 电力电子变压器隔离级

假定PET隔离级变换器内部无损耗,得到传输有功功率,其电流表达式为

式中:i1、i2——PET隔离级DAB输入、输出的平均电流;

U1、U2——变换器一次、二次侧端电压;

n——高频变压器变比;

fs——开关频率;

D1、D2——双重移相控制下的移相比。

建立DAB的等效模型如图5所示。

图5 DAB等效模型Fig. 5 DAB equivalent model

2.4 电力电子变压器逆变级

文中参考贾昊松[10]建立的低压级数学模型,定义一个开关函数为

建立在abc坐标系下的数学方程为

(1)

式中:uoa、uob、uoc——逆变器各桥臂电压;

ioa、iob、ioc——逆变器输出电流;

iia、iib、iic——滤波电路电感电流;

Udc——低压直流电压。

假定Wn为桥臂的开关函数,其表达式为

(2)

联立式(1)(2),得:

通过坐标转换得到dq坐标系下的电路微分方程为

式中,ω——交流电压基波角频率。

3 级联型PET系统拓扑及改进控制方式

采用电力电子变压器结构为:高压级输入由N个H桥串联组成的H桥串联的(CHB)级联结构,以及由双有源桥DAB并联组成的隔离级,低压逆变级为逆变电路。

3.1 改进PET隔离级控制方法

控制方法主要有三种:其中单移相控制,控制简单,但该控制下变换器的效率偏低。三重移相控制的变量偏多且不易应用于实际中。文中所选控制为双重移相控制,双有源桥DC-DC变换器如图6所示。双重移相控制波形如图7所示。

通过控制变换器两端电压的相角来调节传输功率。计算出图7两种控制情况下的传输功率,双重移相控制下的传输功率为

图6 双有源桥DC-DC变换器Fig. 6 Dual active bridge DC-DC converters

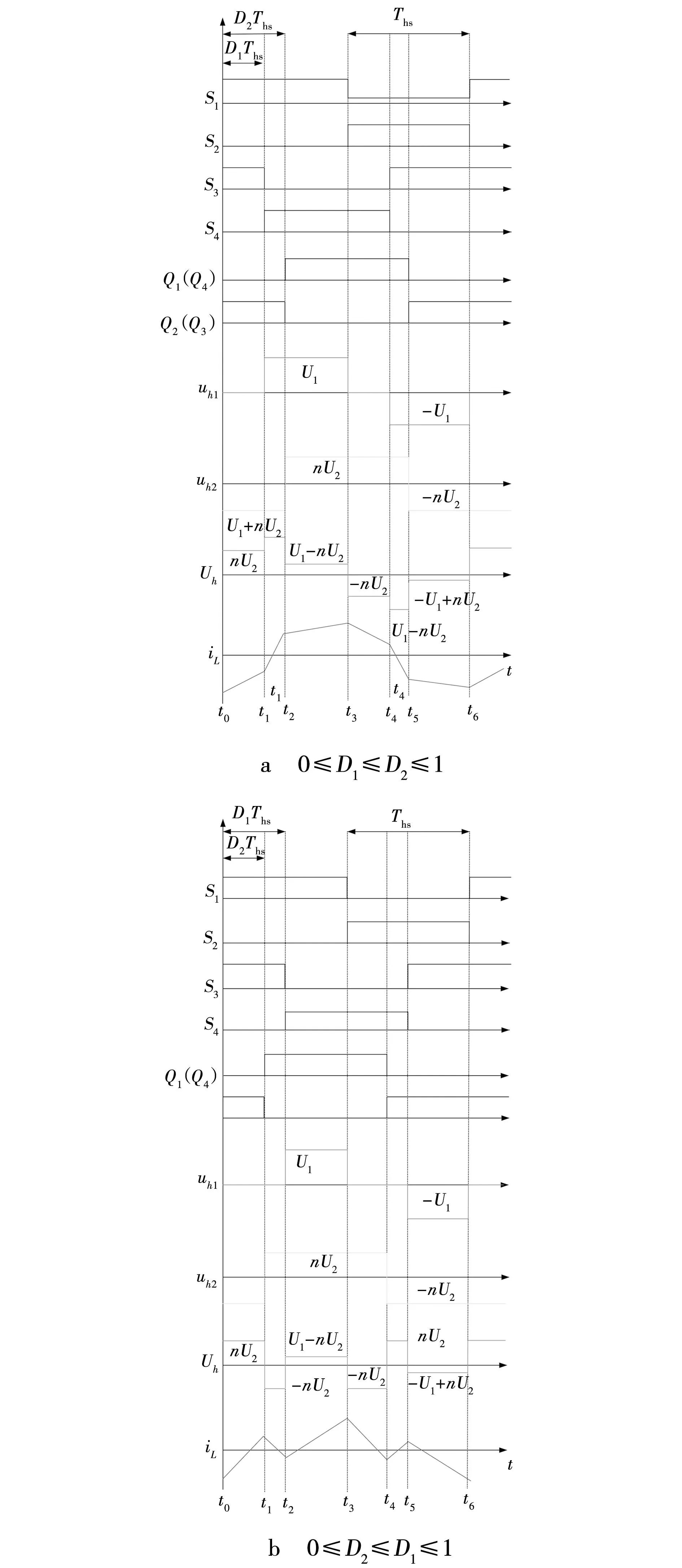
图7 双重移相控制波形Fig. 7 Double phase shift control waveform

优化控制方法是通过改变移相比的方式,通过分析D1、D2的扰动对传输功率(pDPS)和回流功率(rDPS)的影响,得到满足条件的D1、D2控制组合。

D1、D2与传输功率和回流功率的关系为

ΔpDps=pDps(D1+ΔD1,D2+ΔD2)-pDps(D1,D2),

ΔrDps=rDps(D1+ΔD1,D2+ΔD2)-rDps(D1,D2)。

通过偏微分进一步探究控制变量D1、D2微小波动变化时对pDPS和rDPS的影响。假设ρ为评价指标,来判断当D1、D2发生变换时的影响。

式中,Dk——对应控制变量D1和D2,k=1,2。

若D1和D2的组合唯一,但ρ不相等,则

通过上述分析,当D1和D2组合确定时,改变D2比改变D1引起的回流功率的变化要更加明显。在确定D1和D2组合的附近,D1增加的同时减小D2,D1+ΔD1和D2-ΔD2,使得(D1、D2)与(D1+ΔD1,D2-ΔD2)对应的传输功率相等。

pDps(D1+ΔD1,D2-ΔD2)≈pDps(D1,D2)-

rDps(D1+ΔD1,D2-ΔD2)≈rDps(D1,D2)-

D1、D2组合下的传输功率相等,则

整理得:

rDps(D1,D2)>rDps(D1+ΔD1,D2-ΔD2)。

可以发现,D1+ΔD1和D2-ΔD2组合产生的回流功率小于D1和D2组合,那么前者的组合要优于后者。为找寻最优组合需要进一步探索控制变量D1和D2之间的关系,即:

ρ(1)=ρ(2)。

D1和D2之间的关系为

(3)

得到的优化控制方案为:通过单闭环控制D2,使输出电压为一定值,再通过得到的式(3)来实时计算出D1的取值,从而得到D1、D2的最优组合,降低变换器回流功率。

3.2 优化控制策略

优化控制策略如图8所示。搭建DC-DC变换器仿真模型参数:一次侧直流端电压500 V,二次侧直流端电压200 V,变压器变比为3,电容C1、C2为 15 mF,等效电感为350 μH,二次侧负载电阻为10 Ω。

图8 优化控制策略Fig. 8 Optimized control strategy

优化前、后输出功率仿真波形如图9所示。图中负值部分为回流功率,优化目的就是为降低回流功率。通过比较可知,优化前的输出功率最小值约为-5 kW,优化后输出功率最小值约为-1.5 kW,优化后的移相控制后能够减小变换器产生的回流功率。

图9 优化前、后输出功率Fig. 9 Optimize front and rear output power

4 仿真结果与分析

将改进后的DC-DC变换器控制策略应用到PMSG-PET系统中。考虑到风速变化对电力电子变压器接口的PMSG风电系统的影响,对风速变化进行仿真。假设系统运行至4.2 s时风速由开始稳定的12 m/s跌落至9 m/s,4.4 s时又回升至12 m/s模拟了风速变化的情况。

PMSG-PET系统仿真参数:网侧线电压有效值10 kV,电压频率50 Hz,网侧滤波电感5.45 mH,变换器电容15 mF,级联H桥电容5 000 μF,PET额定容量1 600 kVA,PMSG额定风速12 m/s。PMSG-PET系统仿真结果如图10所示。网侧电压与电流波形仿真结果如图11所示。

图10 PMSG-PET系统仿真Fig. 10 Simulation of PMSG-PET system

由图10可见,风速稳定时,系统的输出功率能够稳定,风速变化较大时系统能够跟随响应,输出功率受到波动扰动小。当PMSG风力发电系统通过PET为并网接口时能够应对风速变化,具有一定的抗扰动能力。

图11 网侧电压与电流波形Fig. 11 Grid side voltage waveform

从图11可知,网侧交流电压与交流电流三相对称。提供稳定电压使PMSG风力发电系统正常运行。风力发电系统中的电容电压趋于稳定,PET高压级级联H桥的电压波形也是稳定的,可以保证高压级的正常稳定工作。

5 结 论

(1)在双重移相控制的基础上,优化了电力电子变压器的控制方法,通过改变移相比D1、D2,计算出移相比D1、D2的最优组合。仿真表明,改进后的双重移相控制方法能够有效降低系统的回流功率。

(2)建立了PMSG-PET系统的仿真模型。仿真结果表明,改进控制策略后的电力电子变压器作为PMSG风电系统接口时,系统在正常电压下能够稳定运行,而且能较好地应对风速变化带来的影响。