基于平均速度分析的近地表纵波速度反演

王延光, 梁鸿贤, 芮拥军, 王胜阁, 王姣, 孙成禹

1 中国石油化工股份有限公司胜利油田分公司, 东营 257000

2 青岛黄海学院智能制造学院, 青岛 266427

3 中国石油大学(华东)地球科学与技术学院, 青岛 266580

0 引言

对于石油勘探而言,近地表纵波速度较横波速度在静校正、速度建模等实际应用中更加重要(Liu and Owusu, 2005; Yang et al., 2018).纵波速度可以通过层析反演(Liu et al., 2018, Hu et al., 2021)、微测井(Miller et al., 2018)、小折射等(Re, 2018)获取,也可以通过独立数据获取泊松比结合横波速度结构来获取(Strobbia et al., 2010),但得到的速度结构往往不如面波勘探获取的横波速度结构精细.

现阶段面波勘探目的为获取不同深度横波速度结构(张辉等,2020;高天扬等,2021;李彪等,2021),主要通过计算其中隐含的频散曲线进行横波速度与厚度信息反演(于东凯等,2018;高旭等,2021;陈春林等,2023),但频散数据对于纵波速度的敏感度非常小,纵波速度对于频散数据的影响相对于横波速度与层厚几乎可以忽略不计(Nazarian, 1984; Xia et al., 1999),在横波速度结构反演时往往直接给定,而直接通过频散数据获取纵波速度非常困难(Barreto, 2013).

借助面波获取纵波速度往往需要增加其他信息.现阶段面波与初至信息联合反演成为了纵波速度反演的新方式(Boiero and Socco,2014;傅磊与刘四新,2016;陈淼等,2022;Wang et al., 2023).此外,实验证明反演过程中泊松比的给定会影响横波速度结构计算的效果(Foti and Strobbia, 2002),为了直接通过面波频散数据获取纵波速度,学者们开始研究频散信息中存在的可能对泊松比比较敏感的信息.

频散信息应用于泊松比计算的一个重要突破是Pelekis和Athanasopoulos(2011)发现了探测深度的经验估计对于泊松比较为敏感,Pan等(2013)提出了探测深度系数与泊松比之间存在经验线性公式.这些工作没有直接得到纵波速度,但是却找到了频散数据中隐藏的对纵波速度敏感的关键信息.Socco等(2017a,b)对于面波波长(W)与探测深度(D)之间的关系做了具体的分析,说明了W-D关系与泊松比之间的稳定关系,提出了视泊松比的概念,通过计算得到的泊松比反推了纵波速度.Anjom等(2021)提出了视泊松比法进行近地表速度结构重建的具体流程,对不确定性进行了对比,并于次年将该方法应用于巴布亚新几内亚,获取了地下10～70 m处的纵波速度模型.

实践证明,视泊松比法获取的纵波速度模型仍然存在一定误差,尤其是在中间层纵波速度的计算中.本文在该研究的基础上,进一步证明了W-D曲线对于深层纵波速度较为敏感,而W/D-D曲线对于浅层纵波速度较为敏感;结合蒙特卡洛反演方法(Socco and Boiero,2008),提出了以W-D关系与W/D-D关系相结合的纵波速度直接反演方法.合成数据测试说明,若将W-D和W/D-D曲线同时加入目标函数进行反演,纵波速度反演结果较为精确.本文随后将该方法应用于实际数据中,并将纵波速度反演结果与微测井数据进行了对比.

1 基于W-D曲线的纵波速度直接反演

由于W-D曲线与对于泊松比的变化非常敏感(Socco et al., 2017b),本文根据这一关系,首先提取W-D关系曲线,分析对于泊松比的敏感度.由于根据频散信息可以获取较为准确的横波速度与厚度信息,因此若通过W-D曲线直接反演获取较高精度的泊松比信息即可获取纵波速度信息.

(1)W-D关系与泊松比敏感度分析

本文通过一维层状速度模型来阐述该方法的基本原理,设计了速度递增模型(模型1)、夹低速层模型(模型2)与夹高速层模型(模型3),每个模型半空间以上存在五层上覆地层,不同模型层厚一致,半空间上覆地层厚度分别为3 m、12 m、16 m、23 m、30 m,横波速度模型见图1,每层密度均为2000 kg·m-3,泊松比为0.25,对于给定的一维速度模型,速度模型某一深度的横波平均速度(VSz)定义为厚度与单程走时的比值：

(1)

其中,n为总层数,hi与VSi分别为第i层对应的地层厚度与横波速度.然后通过波长与相速度的关系来显示基阶频散曲线,寻找横波平均速度曲线与频散曲线中速度相同时对应的深度(D)与波长(W),即可得到该模型的W-D关系曲线(图2).因该曲线只对应基阶频散曲线,因此本文中频散曲线均只代表基阶频散曲线(Socco et al., 2017b).

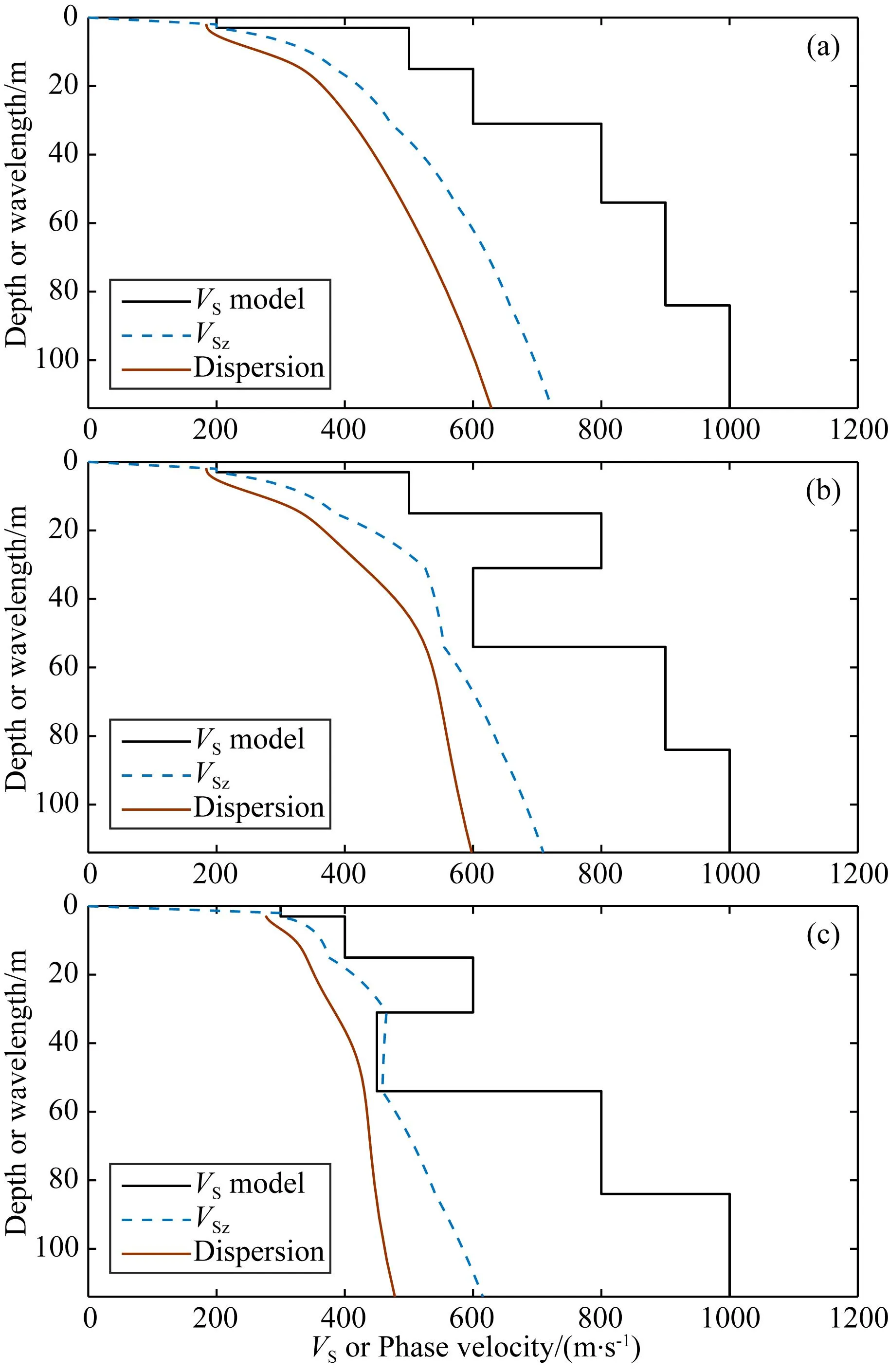
图1 模型参数、横波平均速度与频散曲线示意图(a) 模型1; (b) 模型2; (c) 模型3.

根据Socco和Comina(2015)的研究,在横波速度值不变的情况下,设定各层泊松比变化范围为0.05～0.45,计算对应的W-D曲线如图3所示,可知W-D曲线对于介质的泊松比较为敏感,因此提出了视泊松比的概念,首先通过频散曲线反演获取横波速度与层厚,计算VSz以获取实际W-D曲线,将该曲线与图3中所示曲线簇进行深度的一一对应以获取每个深度的泊松比估计,以此计算模型的纵波速度结构,但是该方法在表层与最深层处计算校准,中间层存在误差.

图2 三种模型的W-D关系曲线

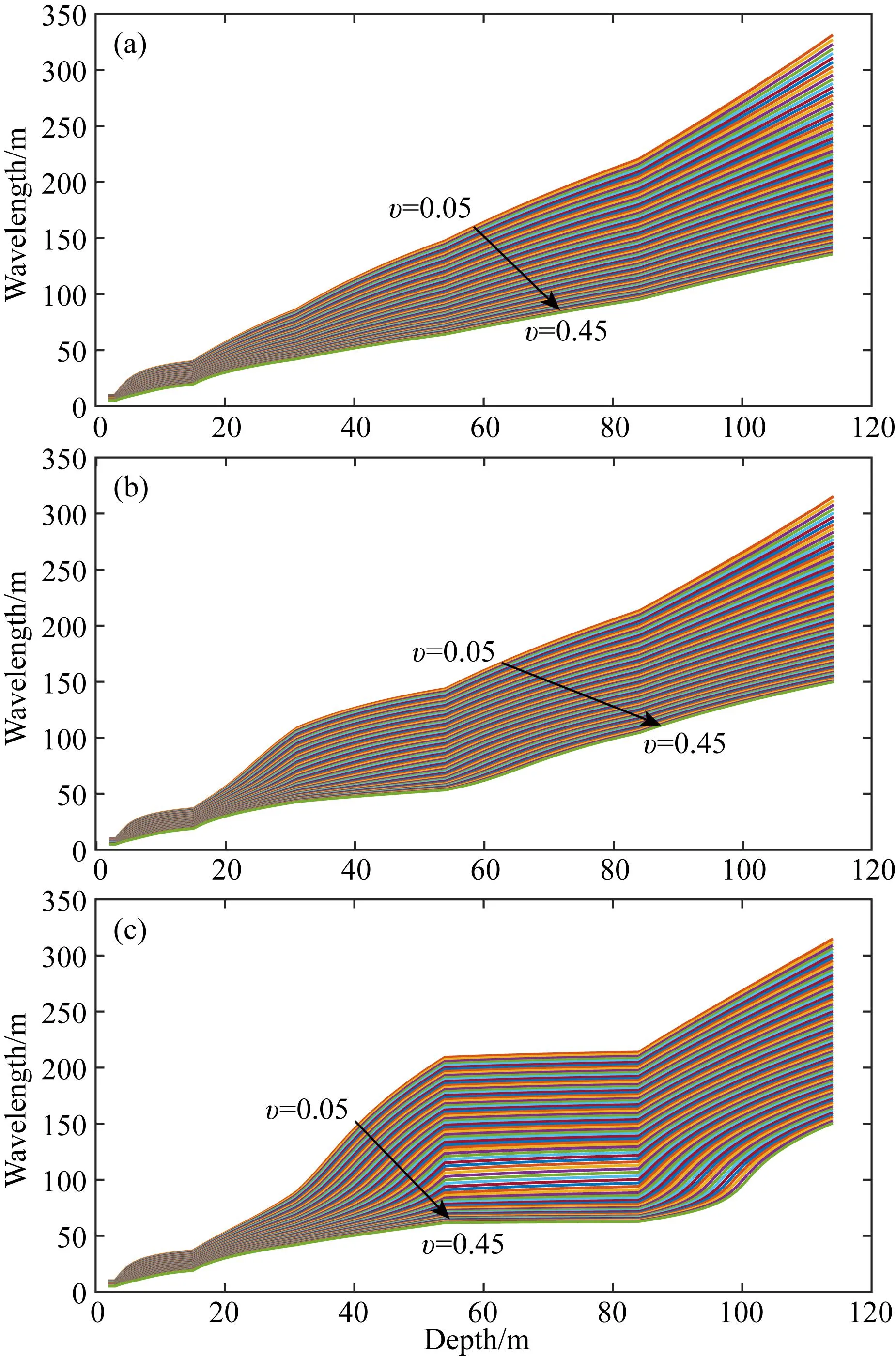
图3 泊松比对于W-D曲线的影响(a) 模型1; (b) 模型2; (c) 模型3.

(2)W-D曲线直接反演

本文尝试直接通过面波获取的频散信息进行纵波速度反演,在横波速度、层厚与密度均确定的情况下,设定各层泊松比υ分别为0.45、0.3、0.3、0.25、0.25、0.25,相应纵波速度为

(2)

采用遗传算法(Holland, 1975)通过W-D曲线直接反演VP,共设置迭代15代,每一代种群数量为90,纵波速度搜索范围为实际纵波速度±500 m·s-1,设定目标函数为

(3)

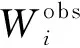
图4 根据W-D曲线所获取的三种模型纵波速度直接反演结果(a)、(c)、(e) 目标函数的拟合情况; (b)、(d)、(f) 纵波速度反演结果.

根据反演结果可知,在目标函数已经拟合非常好的情况下,所获得的纵波速度模型误差非常大,该反演过程是不可接受的.究其原因,W-D曲线中深度较浅段对于纵波速度变化不敏感,纵波速度变化时W-D曲线较浅段变化非常小.

2 纵波速度反演方法的改进

本文根据图3注意到,随着泊松比的变化,深度较浅段中W-D曲线斜率变化较大,设定第i个深度点的W/D值的定义为

(4)

其中,Wi与Di分别为第i个深度点对应的波长与探测深度,可知浅层部分W/D的值变化较为剧烈,相对应的W/D-D曲线如图5所示.

图5 三种模型的W/D-D曲线(a) 模型1; (b) 模型2; (c) 模型3.

由图5可知,W/D-D曲线对于深度较浅处泊松比变化较为敏感,而对较深处泊松比变化欠敏感,因此我们将式(3)进行了改进,提出了一种将W-D数据与W/D-D数据均加入目标函数的新型定义法：

(5)

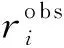
根据反演结果可知,在两种曲线均拟合较好的情况下,可以通过新型目标函数有效实现纵波速度的直接反演,反演结果误差较小.为进一步体现反演方法的有效性,扩大纵波速度搜索范围,改为速度随深度线性变化的趋势作为界限,获取的反演结果如图7所示.由于W-D曲线与W/D-D曲线均拟合较好,仅显示反演结果.

为了对比不同方法的反演效果,定义纵波速度反演准确度为

(6)

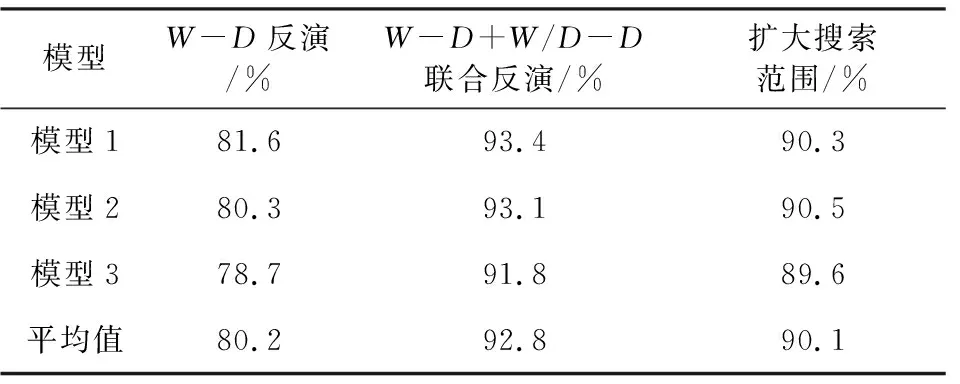
表1 不同目标函数反演结果准确度对比Table 1 The inversion results accuracy comparison of different objective functions

根据以上纵波速度反演模型测试准确度分析可知,本研究提出的新的反演算法可以将纵波速度反演准确度提高至90%以上,有效实现了纵波速度的直接反演.且对比于传统的视泊松比的方法(Socco and Comina, 2017),本次反演结果中间层与表层和底层反演精度没有显著差别,整体反演效果均较好.

根据以上分析,建立基于频散信息获取纵波速度或泊松比的方法过程如下：

(1)根据原始地震记录获取频散数据并进行反演获取横波速度剖面,包括各层横波速度与厚度.

(2)根据横波速度剖面计算各个深度的平均速度并结合频散数据获取W-D曲线与W/D-D曲线.

(3)将W-D数据与W/D-D数据相结合组成新的目标函数并通过全局搜索算法获取使目标函数达到极小值时所对应的纵波速度剖面.

3 敏感度分析

由于W-D曲线中浅层部分的影响占比非常小,且W-D曲线的计算需要借助平均速度,浅层速度反演不准确会导致平均速度计算的误差累积.本文首先提出了基于W-D曲线与W/D-D曲线联合反演的方法计算纵波速度,由于不同目标函数的定义本质上都是为了准确拟合W-D曲线,为了说明W/D-D曲线在反演中的作用,本节进行了敏感度分析.

采用上节中的三种模型,图8为泊松比变化时(0.05～0.45)归一化的不同目标函数(式(3)、(5))变化情况,可以看出本文提出的目标函数定义法可以有效平衡浅层速度与深层速度在W-D曲线反演中的权重.

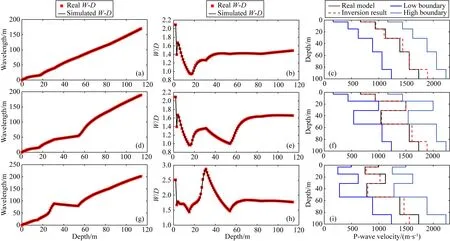
图6 采用新型目标函数定义法的三种模型反演结果(a)、(d)、(g) W-D曲线拟合情况; (b)、(e)、(h) W/D-D曲线拟合情况; (c)、(f)、(i) 纵波速度反演结果.

图7 扩大搜索范围后的三种模型反演结果(a) 模型1; (b) 模型2; (c) 模型3.

为了分析不同目标函数对于不同深度纵波速度的敏感性,定义敏感度参数为纵波速度变化导致的目标函数的变化率：

(7)

(8)

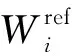
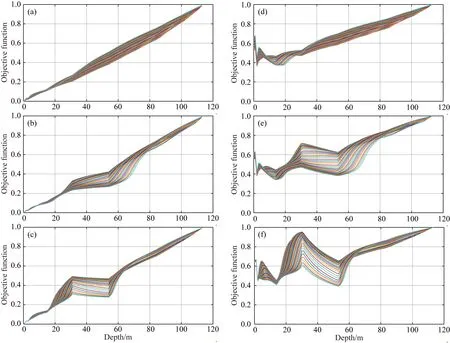
图8 不同目标函数随泊松比变化情况(a)、(b)、(c) W-D与W/D-D联合反演目标函数; (d)、(e)、(f) W-D反演目标函数.

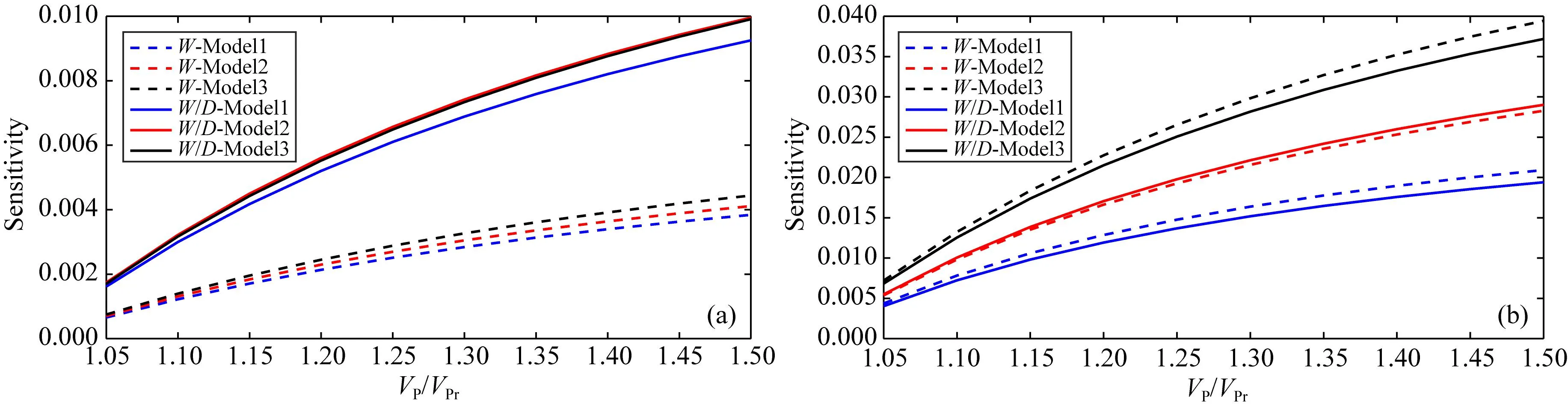
图9 不同目标函数对于纵波速度变化的敏感度分析(a)与(b)分别为第一层与第四层的分析结果.

根据敏感度计算结果可知,目标函数改变后,三种模型浅层纵波速度敏感度明显提高,深层纵波速度敏感度小幅度降低,浅层敏感度与深层敏感度的差距缩小,提高了整体反演精度.

此外,在计算W-D曲线时,由于波长计算需要频率与相速度的关系,存在W-D曲线计算中深度的最小值vmax/fmin,小于该深度的地层在W-D曲线上无法直接体现出来.但在反演过程中,表层速度对于W-D关系的计算非常重要,表层速度的不准确会导致横波平均速度VSz产生误差累积.因此若W-D关系可以拟合成功,可以认为所获取的表层速度是准确的.

4 实际数据测试

在石油勘探中,瑞雷波频带范围较窄,频率较低,主频一般在10 Hz以下.由于低频部分较强,因此探测深度可以达到几百米,但石油地震勘探中瑞雷波勘探的地层分辨率低于工程地震勘探.本次纵波速度反演数据测试采用胜利油田某区块炸药震源数据(图10a、b).由原始数据可知,瑞雷面波发育良好,且为了提高瑞雷面波的勘探精度,单炮的记录长度加长到12s,采样间隔为1 ms.实际数据包含两条测线,测线一激发116次,测线二激发134次,为方便频散提取与横波速度反演,统一采用单边地震数据.

图10 主动源数据以及频散曲线提取(a)、(b) 测线一与测线二单炮原始数据; (c)、(d) 测线一与测线二单炮频散数据提取; (e)、(f) 测线一与测线二提取的全部频散曲线.

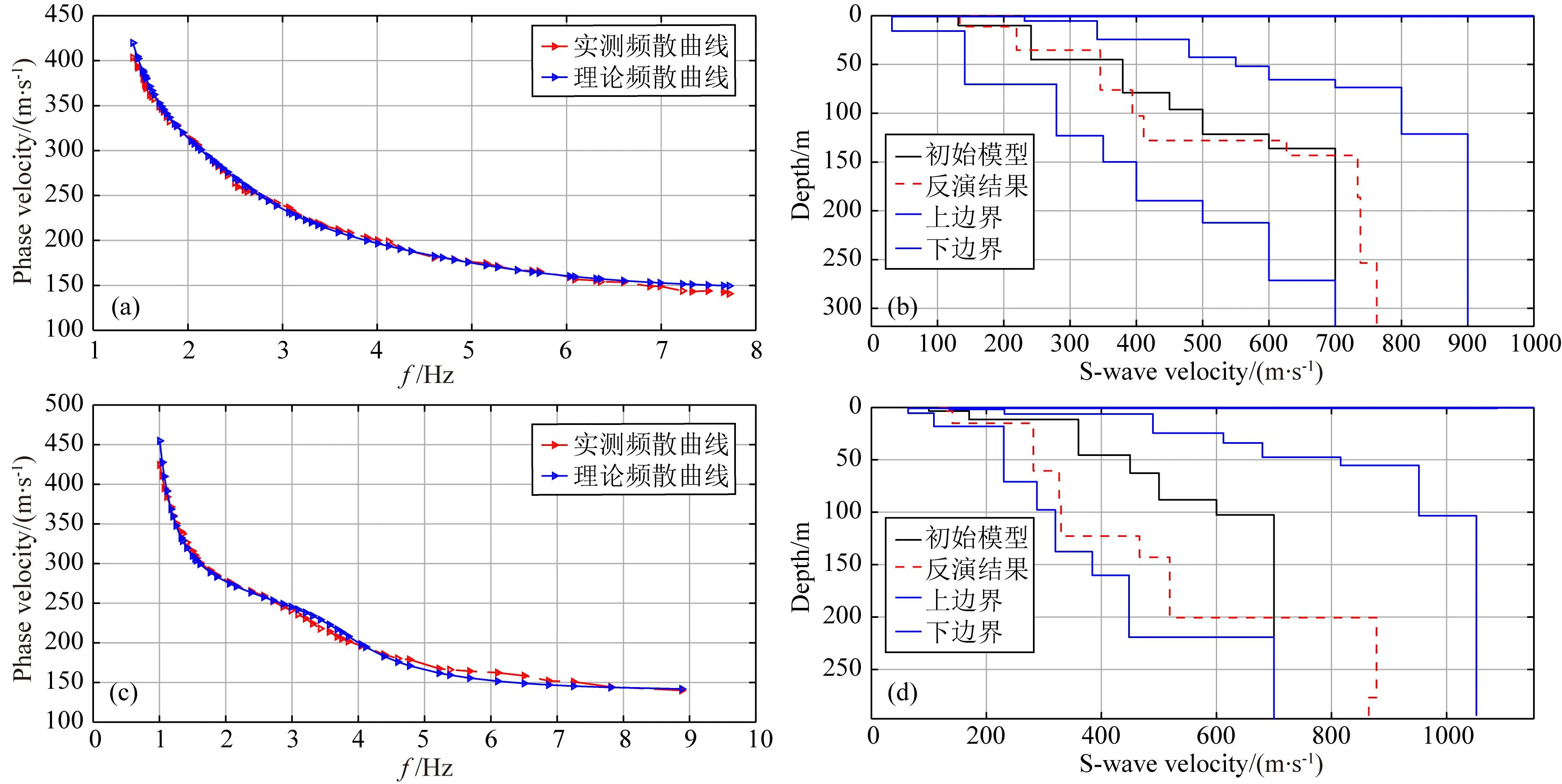
图11 频散曲线反演结果(a)、(c) 频散曲线拟合情况; (b)、(d) 横波速度反演结果.

图12 根据面波信息获取的二维横波速度剖面(a) 测线一; (b) 测线二.

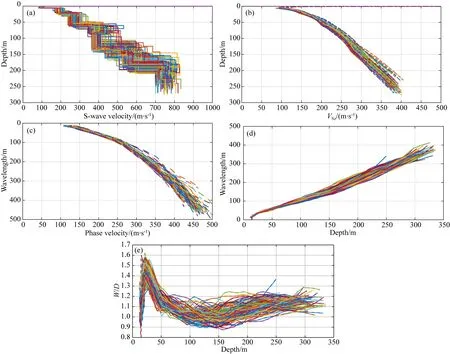
图13 测线一WD信息提取(a) 获取的横波速度; (b) 平均速度计算结果; (c) 频散曲线对比情况; (d)与(e) 分别为获取的W-D曲线与W/D-D曲线.

图14 测线二WD信息提取(a) 获取的横波速度; (b) 平均速度计算结果; (c) 频散曲线对比情况; (d)与(e) 分别为获取的W-D曲线与W/D-D曲线.

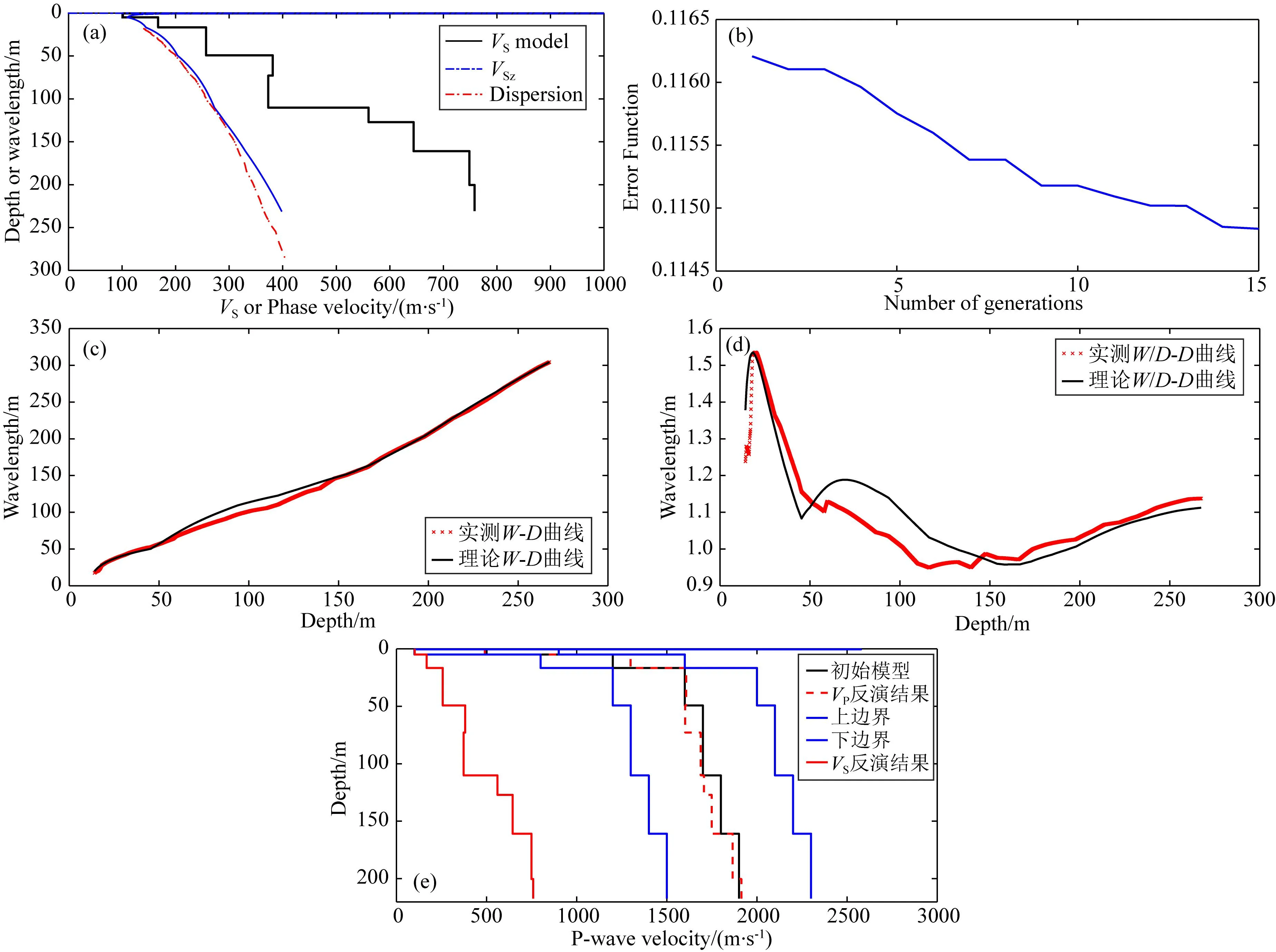
图15 纵波速度反演结果

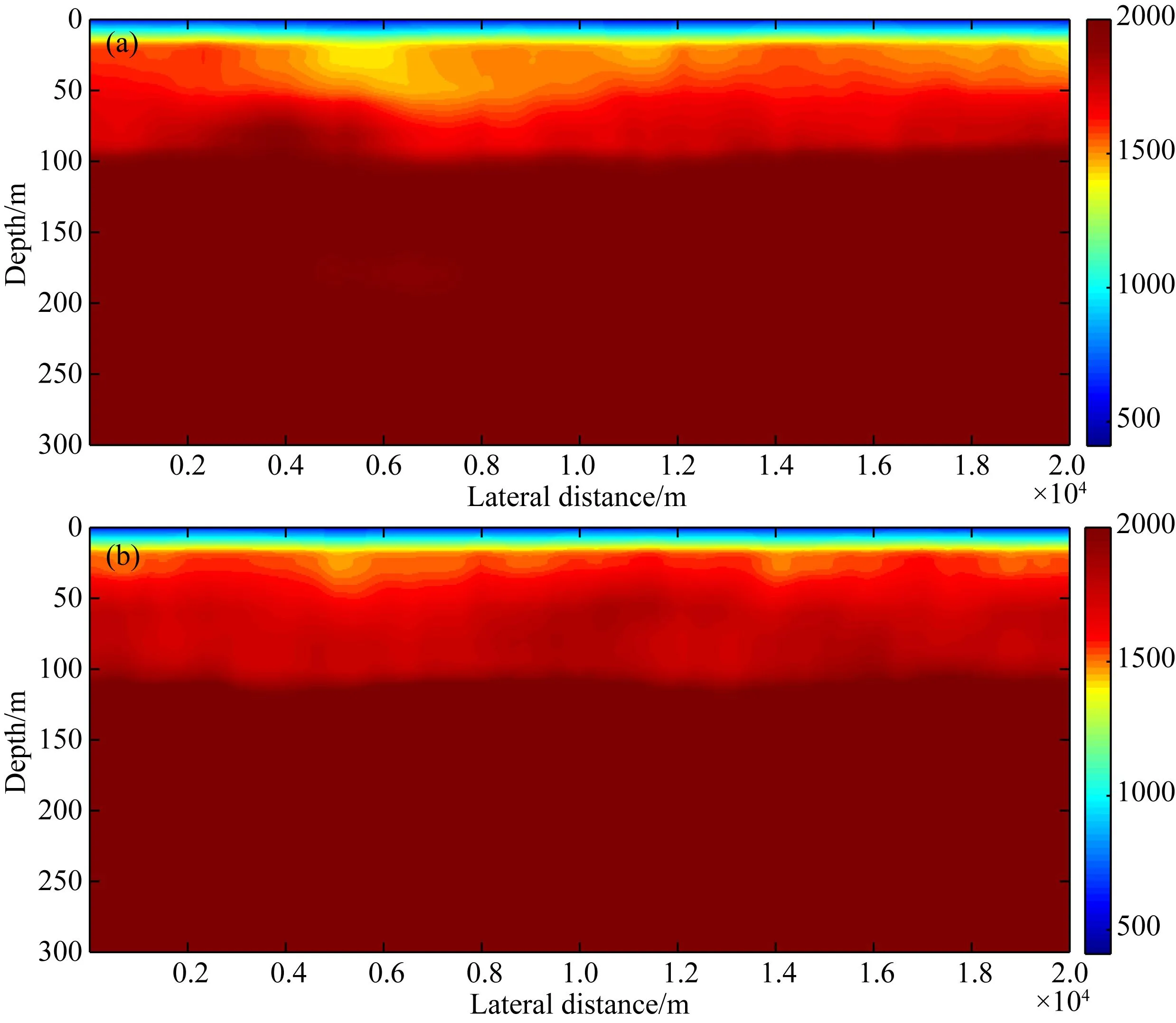
图16 根据面波信息获取的二维纵波速度剖面(a) 测线一; (b) 测线二.

图17 根据微测井信息获取的二维纵波速度剖面(a) 微测井插值结果; (b) 测线一; (c) 测线二.黄色三角形为图19中速度曲线位置.

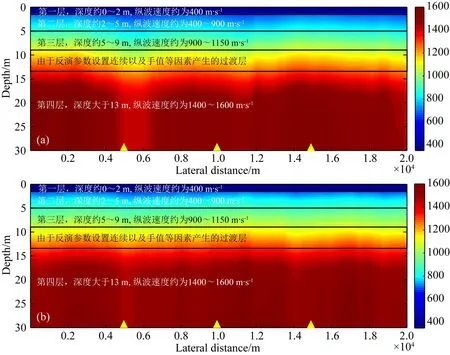
图18 根据面波信息获取的二维纵波速度剖面(30 m)(a) 测线一; (b) 测线二.黄色三角形为图19中速度曲线位置.

图19 微测井数据与纵波速度反演结果随深度变化曲线对比(a)、(b)、(c) 测线一5 km、10 km、15 km处对比结果; (d)、(e)、(f) 测线二5 km、10 km、15 km处对比结果.

(1)横波速度反演

首先通过相移法(Park et al.,1999)对所有面波数据进行频散信息提取(图10),提取面波有效频带为1～10 Hz左右,且同一测线各测点频散曲线形态差异不大.因获取的频散曲线有效频带较低,进行横波速度反演时设置了300 m的探测深度,层数为10层.通过蒙特卡洛全局搜索算法进行频散曲线反演,获得模型频散数据与提取到的频散数据拟合最佳的模型数据组合作为反演结果,同时获取横波速度与层厚信息(图11),并将各点横波速度反演结果与真实坐标一一对应,插值得到横波速度二维剖面(图12).

根据横波速度反演结果可知,该区域近地表横波速度整体呈现随深度递增的趋势,速度范围约为100～800 m·s-1,体现出较好的层状分布.

(2)纵波速度反演与近地表建模

通过波长与相速度的关系来显示基阶频散曲线,寻找横波平均速度曲线与频散曲线中速度相同时对应的深度(D)与波长(W),即可得到该模型的W-D关系曲线.根据图10中各个频散曲线以及反演得到的横波速度对两条测线各个炮集记录进行W-D曲线与W/D-D曲线提取,如图13和图14所示.

根据W-D信息提取结果可以看出,探测区域整体结构较平稳,同一测线W-D曲线与W/D-D曲线形态较为相似,通过上述纵波速度提取方法对该区域各个单炮数据进行了纵波速度反演,计算结果如图15所示.

由于本次反演设置深度较深,W-D曲线与W/D-D曲线无法实现完全拟合,在反演中将目标函数最小值所对应的纵波速度结果作为最终的纵波速度反演结果,并将各纵波速度反演结果根据实际位置组成二维纵波速度剖面,如图16所示.可知表层存在一层厚度约2～3 m的素填土,约3 m以下纵波速度迅速提高,约15 m处纵波速度即达到1400 m·s-1,15～200 m左右纵波速度缓慢增加,达到约2000 m·s-1左右.

为验证本次纵波速度反演的有效性,与该地区微测井数据进行了对比分析.借助微测井解释成果获得了测线处30 m深度的纵波速度剖面(图17).可知该区域30 m深度内主要分为四层,第一层厚度约为2 m,纵波速度约为400 m·s-1,第二层厚度约为3 m,纵波速度由400 m·s-1提高至900 m·s-1,第三层厚度约为4 m,纵波速度范围约为900 m·s-1至1150 m·s-1,第三层至第四层纵波速度存在明显提高,约为1400～1600 m·s-1.

将两条测线0～30 m深度范围内的纵波速度反演结果单独显示(图18),并与图17微测井纵波速度剖面保持相同色标进行对比,两者整体较为吻合.其中第一层至第三层厚度两者基本一致,距地表约13 m以下纵波速度值较为一致.但在约9～13 m之间,由于本次纵波速度反演结果形成二维剖面时进行了垂向插值与横向平滑,剖面上出现了纵波速度的过渡层.图19为相同位置处纵波速度反演结果与微测井数据深度-速度曲线对比图,整体而言,纵波速度反演结果与微测井实测值基本一致,误差较小,体现了本文方法的有效性.

5 结论和认识

本文在已有的面波平均速度分析的纵波速度获取方法基础上,提出了一种新型纵波速度反演方法.该方法设计了W-D与W/D-D相结合的联合目标函数,实现了联合反演,解决了W-D曲线对于浅层纵波速度不敏感的问题.通过模拟数据与实际地震数据的测试,得出如下结论：

(1)W-D曲线对于近地表较浅处纵波速度变化不敏感,对于较深处纵波速度较为敏感,W/D-D曲线对于近地表较浅处纵波速度变化较为敏感,对于较深处纵波速度变化欠敏感.

(2)W-D信息与W/D-D信息组成目标函数明显提高了浅层纵波速度敏感度,对于深层而言,新型目标函数定义带来的敏感度变化较小.目标函数的改变,缩小了浅层敏感度与深层敏感度的差距,提高了整体的速度反演精度.

(3)模型与实际数据测试证明,新型目标函数定义获取的纵波速度与微测井纵波速度有较好的对应关系,相对于传统方法提高了中间层的反演准确度,有效实现了基于面波信息的纵波速度获取.