考虑椭圆模型MW≥5.5地震震源参数时域计算方法

王江, 马强*, 陶冬旺, 章旭斌, 解全才, 林德昕

1 中国地震局工程力学研究所地震工程与工程振动重点实验室, 哈尔滨 150080

2 地震灾害防治应急管理部重点实验室, 哈尔滨 150080

0 引言

随着密集台网设施布设和地震监测技术系统的迅速发展,以地震预警(Earthquake Early Warning,简称EEW)为代表的实时防震减灾技术得到了长足的发展,将由地震预报、地震危险性分析、结构抗震和应急救援组成的防震减灾救灾链条扩展到了震时阶段.震时地震信息(发震时刻,地震位置,震级和地震动场)的快速获取是地震预警系统的核心任务.现行EEW系统采用的策略是通过有限台站、有限波形信息快速定位震源位置并估算地震震级(Kanamori,2005;Olson and Allen,2005;Wu and Zhao,2006;Zollo et al.,2006;马强,2008;金星等,2012);当获取发震位置和震级后,采用“点源”震源模型,将其代入地震动预测方程(Ground Motion Prediction Equation,简称GMPE)预测震中附近目标场地的地震动强度(Wu and Kanamori,2005,2008;Wu and Zhao, 2006;马强,2008;Böse et al.,2012;Peng et al.,2014).预测地震动强度和空间分布的可靠性关乎EEW系统震时防震减灾的成败,直接决定地震警报的发布范围和预警等级.而破坏性地震往往震源规模较大,破裂由一点开始破裂,沿着主破裂方向传播形成较大尺度断层,并向外辐射地震波.因此,破坏性地震的震源能量(震级)、震源区应力降和破裂尺度及方向等震源参数共同控制着致灾地震动的强度和空间分布.EEW系统为提高计算效率采取大量简化处理,将震源视为点源,不考虑震源区应力降和破裂尺度等震源参数,难以保证中、大地震事件中地震动预测结果的可靠性.例如,EEW系统对日本2011年太平洋沿岸的东北地震(MW9.1)的地震动预测出现了严重低估(如Hoshiba and Iwakiri,2011;Hoshiba and Ozaki,2014),导致预警信息和警报发布范围出现较大偏差,其一方面原因是采用有限波形估计的震级偏低,另一方面原因是未考虑震源尺度和方向等关键震源参数.此外,EEW系统估算震级采用的经验统计关系对具有区域特征地震个性化和地震动传播衰减差异考虑不足,这也会对地震动预测造成影响.日本紧急地震速报系统和我国川滇地震预警先行先试区处理结果表明,目前地震预警系统地震动幅值的预测精度多在0.5个数量级,对地震烈度的预测偏差多数在±1度,地震动预测精度明显偏低(Fujinawa and Noda,2013;Kodera et al.,2016;Peng et al.,2020).

确定震源参数是地震学研究中一项基础工作,震后常规获取地震矩、震源尺度和应力降等震源参数的处理方法可分为非参数化方法和参数化方法.非参数化方法通过经验衰减关系估算地震震级等震源参数(Castro et al.,1990;Picozzi et al.,2017).参数化方法采用圆形或矩形断层破裂辐射的体波,通过拟合震源位移谱获取地震矩、震源尺度和应力降(Abercrombie,1995;Zollo et al.,2014;Supino et al.,2019).拟合使用的震源谱是从观测体波谱中消除路径和场地效应的无偏谱,最常用的校正方法是经验格林函数法(Shearer et al.,2019).目前已发展多种校正方法,例如谱分解和全局经验格林函数拟合法(Shearer et al.,2006;Trugman and Shearer,2017),谱比拟合方法(Abercrombie et al.,2017;Ruhl et al.,2017),但是采用不同方法对相同数据计算的应力降结果并不一致,表现出一定程度的不确定性.由于非参数化方法和参数化方法均为震后收集记录,需将时域信号转至频域处理,难以实现震源参数实时计算,所以无法用于EEW系统.近几年,时域快速计算(估算)震源参数的方法也有报道,一种方法是针对中、小地震,根据P波位移增长特征估计震源破裂尺度、应力降和地震矩(Zollo et al.,2022);另一种是根据震源谱ω-2衰减模型,由“圆盘”震源(Brune,1970)中震源参数与地震动均方根参数的约束关系实现震源参数快速计算(Lior and Ziv,2017,2018,2020),该时域方法为震源参数实时计算和考虑震源参数的地震动预测建立了桥梁.以上时域方法研究主要面向中、小震事件,采用“圆盘”震源模型实现震源参数计算.破坏性大震震源断层一般沿着破裂方向的传播距离大于断层的宽度,因此,圆形震源模型不适用描述中、大震震源的破裂面.此外,Kaneko和Shearer(2015)在分析地震应力降和拐角频率等参数估计结果不确定性的原因时,也表明了震源几何形状对拐角频率和应力降的结果存在一定影响.

由此本文引入了符合中、大震震源几何特征的椭圆震源模型,推导了椭圆模型的地震矩、拐角频率、应力降和破裂面积等震源参数与地震动加速度、速度和位移均方根的关系,发展了用于中、大震的震源参数时域计算方法(简称“地震动均方根法”).本文采用日本Kik-net台网82次MW≥5.5地震井下和地表台强震动观测数据验证该方法的可行性,并讨论了场地效应,地震动传播衰减,震源效应和滤波频带等因素对地震动均方根法的影响,分析地震动均方根法的特点和适用性.

1 地震动均方根法

(1)

(2)

其中,W是断层窄边的一半,常数CG是与断层几何形状和泊松比有关的常数(Madariaga,1977).由式(1)和(2)可得应力降：

(3)

中、小地震震源可采用圆形模型(Brune,1970),其震源位移谱的零频极限水平Ω0和拐角频率f0与地震矩和圆形半径的关系如式(4)和(5)所示(Eshelby,1957; Sato and Hirasawa,1973; Madariaga,1976),

(4)

(5)

其中,Uφθ表示辐射花样因子,FS是自由表面因子,ρ是介质密度,C是体波(P波或S波)速度,CS是S波速度,R是震源距,a是圆形震源半径,k是与特定震源理论模型的破裂速度有关的常数.在圆形震源模型中,CG=16/(7π),应力降Δτ和拐角频率f0为

(6)

(7)

大震的震源破裂受地壳厚度的限制,沿着断层走向的尺度一般大于断层的宽度,因此圆形模型不适用描述大震的断层破裂面几何特征.大震震源模型常视为矩形,但观测研究表明,通过测量震源谱的拐角频率仅能近似估算出震源断层长度,很难同时给出矩形震源的长度和宽度(Madariaga,1977).而在椭圆模型中,震源谱拐角频率f0和应力降Δτ与震源尺度关系如式(8)和式(9)所示(Eshelby,1957;Dong and Papageorgiou,2003;Kaneko and Shearer,2015).

(8)

(9)

其中,a,b分别为椭圆形震源的长半轴和短半轴.椭圆面积S=πab,因此当拐角频率已知时,便可近似计算椭圆形震源面积：

(10)

从圆形模型(a=b)到矩形模型(a>b),其常数CG从最小值16/(7π)增至最大值π/2,数值变化不大,约为2倍(Madariaga,1977).椭圆介于圆形和矩形之间,矩形断层中CG值大于任何一个椭圆形断层,因此为简化计算,本文令CG=π/2.将式(9)代入到式(8)可推导出椭圆模型震源谱的拐角频率和应力降关系：

(11)

震源破裂过程控制地震动的强度和空间分布(Hanks,1979;McGuire and Hanks,1980;Luco,1985;Lior et al.,2016),基于圆盘震源模型(Brune,1970)的地震动位移,速度和加速度均方根可由震源谱零频极限水平Ω0和拐角频率f0近似表示为(Lior and Ziv,2017,2018)：

(12a)

(12b)

(12c)

其中T是记录的时长,κ0是场地效应因子.由式(12a)、(12b)和(12c),可导出震源谱参数Ω0和f0的表达式为

(13)

(14)

拐角频率f0的另一种表达为

(15)

由此,圆盘震源模型的震源谱参数Ω0和f0可由位移均方根和速度均方根计算.

参考Kaneko和Shearer(2015)对圆形和椭圆形震源的位移谱的拟合方法,将式(13)和式(15)代入到椭圆模型震源参数表达式(4)和式(11),修正椭圆模型的地震矩M0和应力降Δτ的表达式：

(16)

(17)

其中常数

(18)

与Lior和Ziv(2020)圆盘震源模型震源参数计算公式对比可知,本文针对中、大地震引入椭圆模型修正后,仅改变了应力降计算公式(式17)中的系数,而地震矩和拐角频率计算公式并无变化.因此,仍可在时域内采用地震动均方根参数计算震源参数,计算过程不涉及具有区域特征的先验参数,适用于高时效性的地震预警系统.

2 数据

2.1 数据及来源

鉴于日本Kik-net台网同时配置了地表和井下三分量强震仪,同一台站记录可分析地震动的场地放大效应,本文采用Kik-net井下和地表强震动记录验证地震动均方根法的可靠性.浅源的中、大震破坏力强,影响范围大,破裂过程复杂,因此筛选地震事件和强震动记录的原则如下：地震事件矩震级MW≥5.5,震源深度小于60 km;5.5～6.5级地震记录的震源距设置为100 km,6.6～6.9级地震记录的震源距为150 km,7.0及以上地震记录的震源距为200 km;每个地震事件至少包含4组记录.数据集共选取82次地震,剔除异常记录(如P波头丢失记录和噪声引起P初至难以识别记录等)后,井下记录共计2035组,地表记录共计2031组,每组记录包括两个水平向分量和一个竖向分量.地震的目录矩震级(MWcata)和破裂半持时(Half-duration)由全球矩张量项目(www.globalcmt.org)提供.地震震中(彩色圆形)和台站(灰色三角形)位置分布图和震源深度及记录震源距分布见图1.

图1 地震震中及台站分布图(a)和震源深度(b)及记录震源距统计图(c)

2.2 数据处理

各分向原始加速度记录减掉记录前5 s均值完成基线校正.每组记录的P波初至通过竖向分量拾取,采用长短时比值粗捡拾和AIC精捡拾结合方法执行自动捡拾(马强等,2013),人工检查P波拾取结果并修正因噪声干扰引起的误捡拾.S波到时使用理论到时差确定,其中P波和S波波速见表1,为避免地震定位和走时的误差影响,将理论到时差的90%定为最终P-S到时差.基线校正后加速度记录分别经过一次和两次积分得到速度时程和位移时程.为消除因长周期地脉动等噪声引起的漂移,采用双向巴特沃斯高通滤波器对速度和位移时程滤波,低频截止频率fl为0.02 Hz.加速度、速度和位移时程的三个分量分别代入下式计算地震动均方根：

(19)

其中,参数Prms分别为加速度均方根Arms,速度均方根Vrms和位移均方根Drms.UD,NS和EW分别为竖直向,南北向和东西向地震动.n为输入记录的采样点数.近场P波记录是地震预警系统最常用的数据,所以将P波的地震动均方根参数代入式(15)、(16)、(17)和(10),即可计算震源谱拐角频率、地震矩、应力降和破裂面积等震源参数,其中每次地震破裂面积使用其拐角频率平均值计算.

(20)

(21)

其中,fc是缺失信号的截止频率,本文令fc=max(1/T,fl).T是记录的时长,本文计算震源参数均采用下式计算,

(22)

其中,等号右侧第一项视为震源破裂持时(Hanks and McGuire,1981),f0由式(15)计算;第二项是在数据长度中加入震源距相关项,考虑随地震波传播距离增大引起波包的扩展(Boore and Thompson,2014).

(23)

震源破裂机制复杂,不同震级地震的破裂规模和破裂持时差异巨大,本文主要采用在P波初至后逐步增加的波形获取随破裂演化的震源参数变化过程,进而分析震源破裂的演化特征.地震动均方根法涉及常数按表1取值,每组强震动记录的震源参数计算过程如图2所示.

表1 计算震源参数采用的常数取值表Table 1 Constant values for source parameters

图2 MW6.6地震FKOH05台记录的震源参数计算过程示例(a)—(c) 分别为逐步增加P波的加速度均方根,速度均方根和位移均方根曲线; (d)—(f) 分别为矩震级,应力降和拐角频率计算结果; (d) 中水平虚线为目录矩震级.

3 结果

3.1 震源参数计算

Kik-net台网井下仪器位于孔底,记录噪声低,默认为基岩场地,记录只包含震源和传播路径信息.本节分析井下记录中P波获取的矩震级,应力降和拐角频率等震源参数结果.为消除震源辐射花样的影响,每次地震震源参数取为该地震所有记录计算结果的平均值.图3为MW5.6,MW6.4,MW7.0和MW8.3地震通过地震动均方根法获取的矩震级,应力降和拐角频率的示例.由图可知,地震动均方根法可提供矩震级、应力降Δτ和拐角频率f0随破裂传播的变化过程.随着P波波形的增加,四个震例的矩震级均逐渐趋近于目录矩震级(MWcata),其中前三次地震的矩震级,应力降Δτ和拐角频率f0在破裂半持时前均达到稳定值.而对MW8.3巨震,其震源破裂半持时约为33.5 s,在20 s P波窗内震源参数仍在上升,未完全稳定,这表明对破裂过程异常复杂的大震,通过破裂早期部分波形难以约束整个震源的破裂特征.

图3 四个地震震例的震源参数计算结果灰线为各台记录计算结果,红线为所有记录的平均值;水平虚线表示目录矩震级,竖向虚线表示破裂半持时.

图4汇总了由地震动均方根法计算所有地震的矩震级、应力降、拐角频率和破裂面积随破裂发展的变化曲线.显然,随目录矩震级的增大,震源参数曲线越复杂,达到稳定值的所需P波时长也增加.不同震级地震初始破裂的震源参数存在一定波动,但随破裂发展逐渐稳定,稳定后的矩震级、拐角频率和破裂面积参数随震级的分布体现出明显的相关性,其中最终矩震级几乎完全趋近于目录震级.在图4a中的矩震级增长曲线体现出震源能量的释放过程,下节将对比其与震源时间函数的关系.一般震源区应力降与地震规模无关,本文地震动均方根法获取的早期破裂的应力降曲线波动较大,稳定后的数值分布在0.3～20 MPa范围,82次浅源地震的应力降与震级未表现出相关性.值得注意的是不同震级的震例中初始破裂的应力降多高于后续稳定值(图4b),这可能是由于采用P波时窗长(tW)远小于震源持时,对震源过程采样不足,计算结果可能出现不稳定的情况.Lior和Ziv(2020)认为在这种情况下,应力降表达式可能返回对应于拐角频率f0小于1/tW的非物理结果.但不能排除地震成核后的初始破裂或早期破裂区域的应力降大于整个破裂区的平均值的情况,因为相同均方根参数获取得矩震级增长过程与震源时间函数计算的结果基本一致(图7).

拐角频率变化曲线表明从地震早期破裂辐射P波获取拐角频率均远大于整个破裂的均值;拐角频率的稳定值随震级关系体现出地震的基本规律,地震越大,辐射地震动的低频成分越丰富,拐角频率越低(图4c).由拐角频率均值计算的破裂面积随震级的增加而增大,因地震破裂过程复杂,震时破裂面几何形状并不规则,因此通过拐角频率近似计算的震源破裂面积精度可能较低.

对比2 s、4 s和8 s P波的矩震级结果发现,通过扩大时窗,地震动均方根法获取的矩震级均值与目录震级的分布逐渐接近于1∶1线,提高矩震级结果的可靠性(图5).采用全P波段记录使得大震震级的低估问题得到有效改善.因此,地震动均方根法能够利用P波记录快速可靠地获取表征地震绝对能量的矩震级.

图6进一步展示了所选地震在全P波记录中获取的拐角频率、应力降和破裂面积参数随震级的分布.作为描述地震震源谱的关键参数,拐角频率随震级增大而降低,目录矩震级(MWcata)换算的地震矩和拐角频率的拟合关系式为

(24)

拐角频率的幂次在-4与-3之间,符合地震自相似比例关系(Archuleta et al.,1982;Abercrombie, 1995;Hiramatsu et al.,2002).82次地震的震源区应力降主要分布在0.3～15 MPa之间,接近日本地区地震的统计范围(Oth et al.,2010).按震源深度分类,深度在30 km以内视为地壳事件,大于30 km的为地壳下事件,那么由全P波段计算的震源参数中,相同或相近震级的地壳地震的拐角频率和应力降普遍大于深部的地壳下事件,其中地壳地震的应力降均值约为1.45 MPa,地壳下地震的应力降均值约为3.96 MPa.此外,震级接近的浅源壳震的破裂面积几乎都大于地壳下地震,这也符合日本地区地震基本规律(Oth et al.,2010).

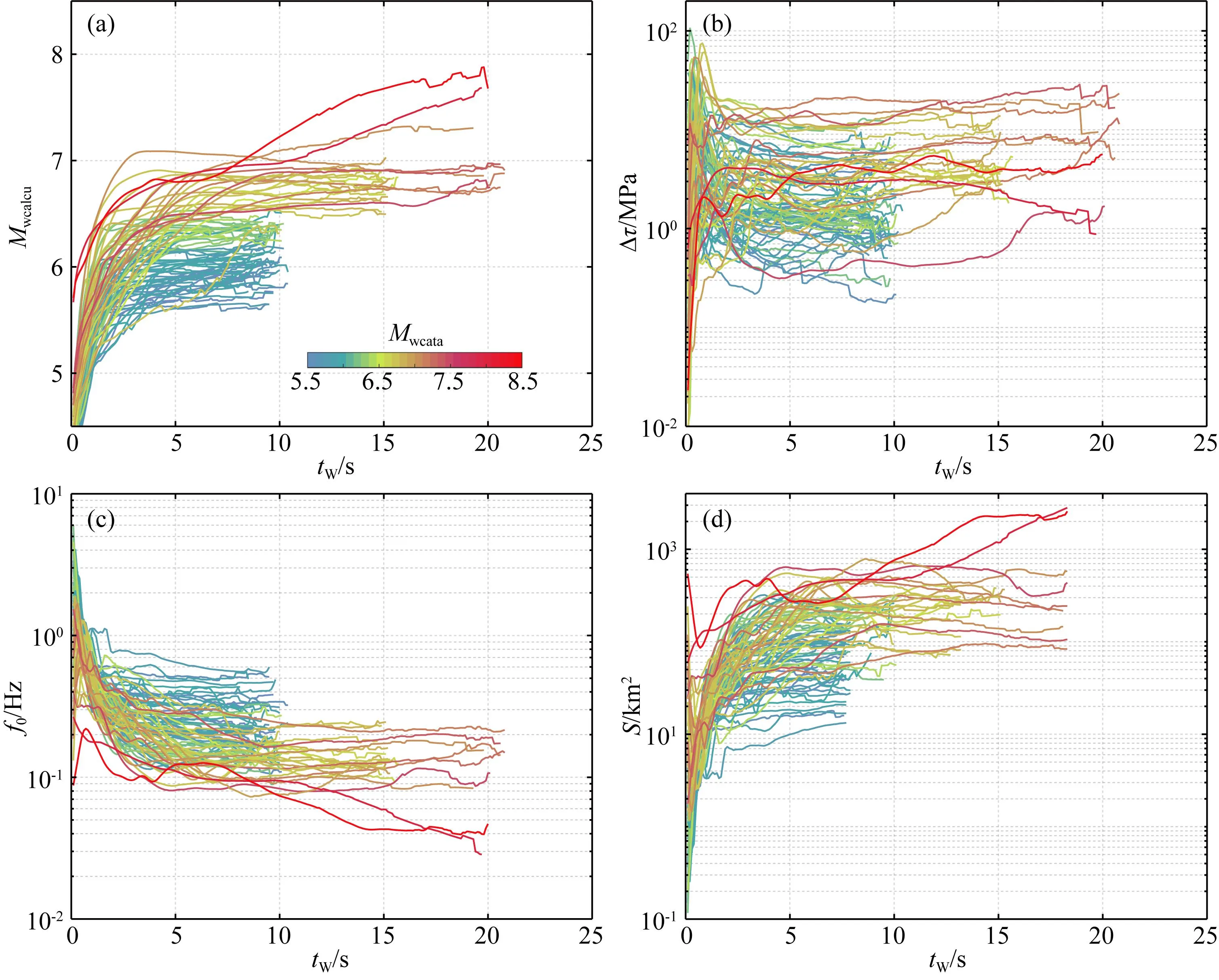
图4 井下P波记录计算的震源参数结果

图5 2 s、4 s、8 s时窗和全P波段的矩震级结果灰点为各组记录计算的矩震级,菱形为每次地震所有记录计算的矩震级平均值,灰色虚线为1∶1参考线.

3.2 地震能量释放过程

中、大地震震源破裂物理过程复杂,震后常用远场测震记录反演获取地震震源能量释放过程,即震源时间函数(STF).目前全球中、大震的震源时间函数SCARDEC数据库已经建立(Vallée and Douet,2016).为验证地震动均方根法获取矩震级曲线是否反映地震能量的释放过程,本节将其与SCARDEC数据库提供的STF进行对比,其中由STF计算的矩震级定义为MW-STF.图7展示了观测记录较丰富的四个地震事件(MW6.6、MW7.0、MW7.4和MW8.3)的震源能量释放过程.由图可知,MW6.6、MW7.4和MW8.3地震的计算矩震级曲线与MW-STF曲线基本一致,地震动均方根法能通过P波记录可靠量化地震能量释放过程,但MW7.0地震的矩震级曲线在局部时间段内(1～6 s)的偏离MW-STF曲线.四个地震震中位置分别对应图1中的地震序号1、2、3和4,对比观测台站位置发现,MW7.0地震的强震台集中分布在震中方位角的一个象限(270°～360°),而其他三次地震的记录至少分布在地震震中方位角的两个象限.地震动均方根法的矩震级计算偏差很可能受辐射花样和(或)破裂方向性效应的影响.由此可知,地震动均方根法对观测台站震中方位角分布比较敏感,当地震的台站方位角分布均匀时,能够通过P波记录快速可靠地量化地震能量释放过程.

图6 由全P波记录获取的拐角频率、应力降和破裂面积结果灰色圆点为各台记录获取的震源参数结果,彩色圆形为各地震所有记录获取参数的均值.

图7 地震能量释放过程灰线为地震动均方根法由每组记录获取的矩震级曲线,黑实线为所有记录的矩震级均值曲线,粉虚线为STF计算的矩震级曲线.

4 影响因素分析

震级表征了地震破裂能量,是地震预警发布的关键地震信息,便于从地震目录中获取,本节以地震动均方根法的矩震级计算结果为例,分析场地效应,地震动传播衰减,震源效应和滤波频带等因素对该方法的影响.

场地效应对地震动影响十分复杂,土层厚度、密实程度、地形地貌都可能会对地震动不同程度的放大,对不同频率成分地震动的放大也有差异.为明确地震动均方根法对场地效应敏感程度,本节简单对比采用井下和地表记录8 s P波获取矩震级的误差.经统计,MW7.0及以下地震震源破裂半持时均小于8s,对该震级段的地震,地震动均方根法计算的矩震级接近于目录矩震级(图8).其中井下记录矩震级结果同目录矩震级的误差介于±0.5之间,平均值为0.07个震级单位(图8a);地表记录矩震级计算误差介于±0.5之间,平均值为0.02个震级单位(图8b).然而大震(MW>7.0)破裂半持时大于8 s,震源破裂规模大,导致从井下和地表8 s P波波形计算的矩震级都偏低.图8c是由井下和地表记录获取的矩震级之差,井下记录计算的矩震级略大于地表记录,矩震级之差介于±0.2之间,平均值为0.09个震级单位.由此可知,地震动均方根法在计算矩震级时对场地效应不敏感,采用井上和地表记录都可获取可靠的地震震级.因此,在EEW系统中,综合考虑时效性和精度要求,地震动均方根法可忽略场地效应影响直接使用地面记录计算矩震级.

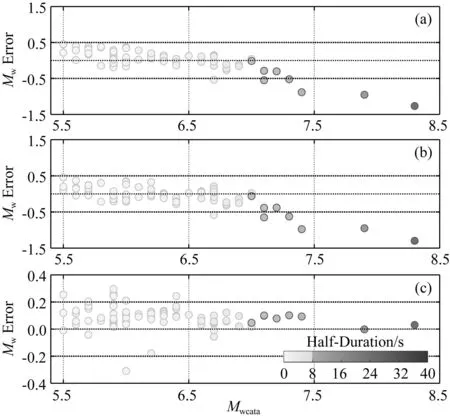
图8 井下和地表记录计算矩震级的误差统计(a) 井下记录计算误差; (b) 地面记录计算误差; (c) 井下记录和地面记录计算误差.

地震动传播衰减是EEW系统Pd方法估算震级的关键修正项,而且往往存在区域特征.震动记录匮乏和地震风险水平较低的地区难以获取Pd经验关系,可能会限制EEW系统应用.若对这类地区采用来自其他区域的先验关系,则需开展专项验证测试工作.地震动均方根法考虑了地震动传播衰减项,即震源距R(式(16)—(17)).图9结果表明地震动均方根法采用井下记录4 s和8 s P波计算的矩震级随震源距分布未出现明显的衰减趋势.因此,地震动均方根法无需再进行地震动传播衰减的校正,放宽了在缺少强震记录地区的限制,有效提升地震预警系统的适用范围.

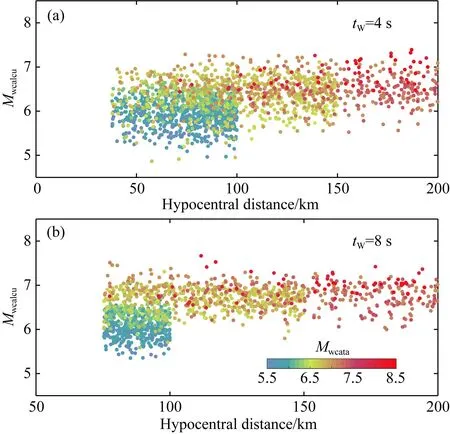
图9 井下记录获取的矩震级随震源距的分布

地震破裂在时间和空间上扩展传播的不对称行为,即地震破裂方向性,常出现于大震中(McGuire et al.,2002;Wen et al.,2015),部分中、小地震的破裂方向性效应也有报道(Kane et al.,2013;Wang et al.,2019).破裂方向性效应往往会引起在破裂传播方向上的地震动持时变短、幅值升高、视拐角频率升高,破裂后方地震动持时延长、幅值降低、视拐角频率降低.地震震源对地震幅值调制的另一种常见的机制为震源辐射花样,常用于量化辐射花样的模型是四叶模型,对震中附近地震动幅值调制多为四象限花样分布.本节选取了4次陆域地震(MW5.5,MW5.8,MW6.8和MW6.9),其台站方位角分布相对均匀,震中位置分别对应图1地震序号5、6、7和8.4次地震井下记录的4 s和8 s P波计算的矩震级随方位角的分布均体现出正(余)弦形式的规律性波动(图10).鉴于传播距离对地震矩影响较小,因此推测这种调制结果可能反映震源的一种或综合效应.其中两次中强震(MW6.8和MW6.9)的矩震级计算结果随方位角波动较大,震源效应更强.因此,如果台站集中分布在较窄方位角范围内,很可能因震源效应造成较大的矩震级计算偏差,如图7b.若计算矩震级随台站方位角的律动是破裂方向性的效应引起的,那么当震中周围台站方位角分布均匀时,可通过矩震级随方位角分布特征,如方向性效应系数Cd,估计出震源破裂方向和破裂方式(单侧破裂还是双侧破裂),这可为实时地震动预测提供至关重要的震源断层参数.

图10 井下记录获取的矩震级随台站方位角的分布及其拟合曲线

强震动记录积分处理时采用了高通滤波以消除因长周期地脉动等噪声积分引起的漂移,但由此也可能滤掉地震动中部分有效低频成分,尤其是破坏性大震.将高通滤波器的低频截止频率设为0.02 Hz和0.05 Hz,分析频带差异对地震动均方根法获取矩震级结果的影响.图11表明井下8 s P波经过fl=0.02 Hz的高通滤波处理能够获取更可靠的矩震级效果.因此,建议选用低频截止频率为0.02 Hz的高通滤波处理记录以保留地震动中有效的低频成分.

图11 滤波频带对地震动均方根法矩震级结果的影响

5 实时震级计算效果

地震动均方根法可通过P波波形快速获取震源参数,为分析其矩震级计算结果的可靠性,本节选用地表记录分别通过估算震级经验方法和地震动均方根法计算矩震级.EEW系统一般采用P波特征参数(峰值参数Pd和周期参数τc等)的经验关系快速估算地震震级.在离线数据中,Pd参数估计震级的精度表现更好(金星等,2012).本节对比全球经验Pd方法(式(25))和地震动均方根法的实时震级估算结果,

MPd=1.23log(Pd)+1.38log(R)+5.39,

(25)

+1.105(±0.126),

(26)

其中MPd是Pd震级,对应日本地震震级Mj,R是震源距(Kuyuk and Allen,2013).为统一震级标度,Pd方法估算的震级MPd通过式(26)转换为矩震级MW(Oth et al.,2010).Pd方法采用垂直向记录,地震动均方根法仍采用三分向记录,用于速度和位移时程的滤波频带与2.2节一致.本节选择4 s和8 s P波对比两种方法的矩震级结果(图12).结果表明,对统一的P波时窗,地震动均方根法计算矩震级的离散性和准确度均优于Pd方法.其中8 sPd参数估算的矩震级普遍高于目录矩震级(图12c),说明估算震级的经验方法需要考虑不同区域地震动衰减规律的差异.因此,在地震风险低和强震动记录匮乏的地区,若采用统一先验关系估算震级,其适用性需要进一步验证.

图12 Pd方法和地震动均方根法计算矩震级结果对比(a)和(c)分别是4 s和8 s时窗的Pd法计算结果;(b)和(d)分别是4 s和8 s时窗的地震动均方根法计算结果,误差棒表示95%置信区间.

6 讨论

鉴于震源几何形状一定程度上影响着拐角频率和应力降等震源参数(Kaneko and Shearer,2015),本文在Lior和Ziv(2020)提出的震源参数算法的基础上,针对中、大震引入了椭圆震源模型,发展了椭圆模型下震源参数的时域算法,其中主要修正项是应力降计算公式,矩震级和拐角频率算法并未改变.

Kaneko和Shearer(2015)开展了震源几何特征对震源谱和拐角频率及应力降等震源参数影响的研究,其对圆形和椭圆形震源辐射体波的位移谱均采用了Brune(1970)提出的ω2震源谱拟合.借鉴这种方法,本文从Brune震源谱出发,在圆形震源模型震源参数与地动参数之间的关系基础上,尝试通过椭圆模型震源参数间的关系,修正中、大震的震源参数计算公式(式(10)、(15)、(16)和(17)),进而实现由时域地震动参数计算震源参数.也可理解为直接利用Brune震源谱拟合中、大震震源谱获取Ω0和f0,然后根据椭圆模型修正公式计算震源参数.

事实上,利用Brune震源谱拟合大震震源谱可能对量化低频幅值水平(Ω0)存在一定误差(Joyner,1984).由于Brune震源谱模型在中低频段高估观测谱幅值,因此在Brune模型的基础上发展了适用于大震的双拐角震源谱模型(如陶夏新和王国新,2003),以修正Brune模型Ω0的拟合误差.与低频幅值水平Ω0相对应的震源参数是地震矩(式(4)),本文推导的地震矩计算公式(式(16))在圆形和椭圆形震源模型下是一致的,也就是引入椭圆模型并未改变该公式.为明确由地震矩计算公式(式(16))对大震适用性,本节补充了日本82次中、大地震由全波列记录计算的矩震级结果(图13),具体计算方法参考Lior和Ziv(2020),相关常数按表1取值.计算结果表明当采用足够长度记录计算的矩震级和目录矩震级基本一致,未出现明显偏差,证实了本文方法的可靠性.但是我们也注意到不论是采用P波还是全波列计算82次地震的矩震级结果确实存在略微偏离1∶1线的趋势(图5和图13),且随震级增大,计算矩震级向下偏移趋势越明显.这可能是采用Brune震源谱模型拟合中、大震震源谱参数Ω0的误差引起的.

地震动均方根法推广最大的限制性因素是场地效应.第4节已明确了场地效应对矩震级结果的影响较小,在此分析场地效应对拐角频率和应力降和破裂面积的影响.图14为地表和井下全P波记录计算震源参数的比值.对比结果表明,场地效应使拐角频率放大约1～3倍,震级越大,影响越弱;应力降的变化范围较大,放大约为1～12倍,同样震级越大,场地效应的影响降低.而由地表记录获取的破裂面积普遍小于井下记录结果.当震级相近时,场地效应对深度更大地震的拐角频率和应力降影响略高于浅源地震.根据式(11)可知,当场地效应使得拐角频率增加2倍时,计算应力降将增加8倍,这是应力降放大倍数远大于拐角频率的主要原因.传统采用频域参数法拟合震源谱获取的应力降结果差异也比较大,表现出一定的不确定性,这主要是因为应力降是高度依赖于模型的(Shearer et al.,2019).值得注意的是,对震级大于6.5的地震,场地效应对震源参数的影响变弱,这可能是由于大震辐射地震波频率偏低,与场地的卓越频率相差较大,地震记录的视拐角频率受其影响弱化引起的.因此对于大震,本文发展方法可以通过地面记录快速获取相对可靠的震源参数.

图13 井上台10 s、20 s、40 s和全波列的矩震级计算结果灰色圆点为台站记录计算矩震级结果,菱形为各地震事件的平均矩震级.灰色虚线为矩震级1∶1线.

图14 82次地震地表和井下全P波记录计算拐角频率、应力降和破裂面积的比值

以上仅对地震动均方根法主要影响因素展开讨论,地震动均方根法推导过程还涉及一些简化假定,如壳幔介质中P波和S波波速随着深度增加而增大,而本文采用固定数值,势必引入计算误差.P波常数k的取值是来自破裂传播速度Cr=0.9CS的假设,实际地震破裂传播速度存在差异,因此,在震源参数计算中常数k也会引入误差.除此之外,实际破裂面的几何形状要远比椭圆模型复杂,大震破裂面的长度可能远大于宽度,通过椭圆模型估计应力降和破裂面积可能存在一定偏差.尽管如此,本文结果与日本地区地震震源参数的统计结果对比可知,地震动均方根法能够通过时域近场波形快速获取可靠的震源参数,不仅为EEW系统提供了新方法,还能够量化震源参数随破裂发展的演化过程,为分析地震破裂特征提供了新的途径.

7 结论

考虑中、大震震源几何长短轴差异,在圆盘模型震源参数与地震动均方根的约束关系的基础上,本文推导了椭圆震源模型中震源地震矩、拐角频率和应力降同地震动加速度,速度和位移均方根的约束关系,提出了一种适用于中、大型地震震源参数时域快速估计方法.该方法绕过了传统震源参数的反演或者在地震信号频率域测量的过程,不涉及地震区域特征先验参数,计算方法简便,无需人工参与计算,非常适用于高时效性的地震预警系统.为验证地震动均方根法的可靠性,本文采用日本Kik-net台网MW≥5.5中、大地震的井下和地表强震动记录进行验证.通过对比分析,得到以下结论：

(1)考虑椭圆模型的地震动均方根法能够采用P波波形快速可靠地计算中、大震矩震级、应力降和拐角频率及破裂面积等震源参数;

(2)由全P波段和全波列记录计算的矩震级与目录矩震级基本一致,大震的震级低估得以有效缓解;

(3)由地震动均方根法计算82次地震的拐角频率随地震矩的分布满足地震自相似规律,震源区应力降数值符合日本地区的统计范围(0.3～15 MPa),验证了该方法的可靠性;

(4)地震动均方根法考虑地震动传播距离,其震源参数计算结果可不再做路径衰减项校正;

(5)地震动均方根法对震源效应比较敏感.当震中附近台站方位角分布均匀时,能够通过P波记录快速可靠地量化地震能量释放过程;

(6)场地效应对地震动均方根法影响复杂,其中矩震级计算结果对场地效应不敏感;场地效应对拐角频率和应力降存在一定影响,但随震级的增大其影响变弱.因此对于大震,地震动均方根法可以通过地面记录快速获取相对可靠的震源参数.

致谢感谢日本Kik-net数据中心(https：∥www.kyoshin.bosai.go.jp/)为本文研究提供的强震动数据和全球矩张量项目(https：∥www.globalcmt.org/CMTsearch.html)提供的震源参数.感谢匿名审稿专家为本文提出的宝贵意见与建议.文中部分图片使用通用制图工具GMT(Genetic Mapping Tools)绘制.