21世纪全球三次MW9.0左右地震的孕育过程研究

陈学忠, 李艳娥*, 陈丽娟

1 中国地震局地球物理研究所, 北京 100081

2 重庆市地震局, 重庆 401147

0 引言

地震预测的发展趋势是从经验预测向物理预测过渡,这是业内已达成的共识.物理预测的关键在于了解地震孕育过程的特征和机理.根据岩石力学实验结果,可以认为地震孕育过程主要包含两个阶段：一个是应力积累阶段,另一个是应力峰值点之后的临界状态或亚失稳阶段.一个紧随的问题是：实际地震孕育过程是否与此一致?对这个问题的回答有赖于开展实际震例研究.21世纪全球已经发生过三次MW9.0级左右地震, 为了验证这些地震的孕育过程中,是否存在上述两个阶段,本文将以三次作为震例,对其孕震过程进行分析.

对于应力积累过程,我们需要获取震源处的应力状态.目前,尽管难以直接检测到地下几公里至几十公里的震源处的应力信息,但可以通过b值或视应力进行间接推知,从而得到震源处的应力状态.岩石力学实验中发现b值与应力成负相关关系(Scholz, 1968; Wyss, 1973),b值的变化还与地壳介质非均性有关(Mogi, 1962), 甚至与地热梯度有关(Warren and Latham, 1970).视应力等于剪切模量与地震能量和地震矩之比的乘积,也等于地震效率η乘以断层面上的平均应力(Wyss, 1970a; Wyss and Molnar, 1972).当构造应力增加时,b值降低,同时视应力增加,反之亦然.即,b值与视应力之间存在负相关关系.因此,将b值与视应力进行联合分析,可以在排除其他影响因素的前提下获取震源区的应力状态.已有震例研究表明强震前b值下降,同时视应力上升(陈学忠等, 2021; Li and Chen, 2021; Li et al., 2021).一根立在地上的杆子稳不稳定,只要用手握住它轻轻地摇一摇就知道.如果杆子晃动,它就不稳定.用手握住杆子摇一摇这个动作实际上是在给杆子加上一个微小的作用力.将这个经验应用到震源区稳定性评估,可以认为当震源区被加载到临界状态时,它可能变得极其不稳定以至于发生在它及其附近地区的中小地震会对微小应力变化敏感.由于地球自转速率变化可以在震源断层上引起非常微弱的应力变化(陈学忠等, 2018),因此, 如果震源区处于临界状态, 地球自转速率变化将会触发地震活动,从而使这些被触发的地震与地球自转速率变化之间呈现出显著的相关性.我们可以根据与地球自转相关的地震活动性来评估震源区的临界状态或亚失稳状态.

1 分析方法

1.1 视应力

地震视应力定义为(Wyss,1970b)

(1)

式中,μ为剪切模量(对于地壳介质,μ可取3×104MPa),ES和M0分别为辐射能量和地震矩.视应力计算方法可见Li和Chen(2021).以等地震个数的样本窗口计算平均视应力,将该窗口以相等事件数的增量进行滑动,每个窗口中最后一个事件发生的时间作为计算的平均视应力的时间,这样就可以得到平均视应力随时间的变化.

1.2 b值

采用极大似然法计算b值(Aki,1965)：

(2)

b值的标准差估计主要有以下两种方法.Aki(1965)给出标准差为

(3)

Shi和Bolt(1982)给出的标准差为

(4)

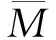
在b值分析中,为了了解b值下降区域与震中之间的可能关系,我们给出震中附近较大区域范围内b值相对下降变化量的空间分布.以一定的经纬度间隔将区域划分成若干网格,以每个格点为中心点,选取适当大小的空间子区域,计算每个子区内地震的b值随时间的变化曲线,按式(5)计算每个b值时间变化呈明显下降变化形态的子区的b值相对变化幅度,并将其作为该子区的中心点处的b值相对下降幅度值,从而可以得到b值相下降变化量的空间分布.

设t1时刻的b值为b1,t2时刻为b2.b值的相对变化量为

(5)

1.3 与地球自转相关的地震活动性

首先根据地球自转速率季节性变化曲线,计算所选取的研究区内发生的每个地震的相位角θ.计算时规定在地球自转速率变化的极大值点处相位角θ=0°,在其左边的第1个极小值处相位角θ=-180°,在其右边的第1个极小值处相位角θ=180°.每个地震的相位角可以根据下式来计算：

(6)

式中,te为某个地震的发生时间,t0为离地震最近的极大值处的时间,t-180和t180分别表示地震前后离地震最近的两个极小值处的时间.对于由N个地震组成的一组地震,可以利用舒斯特(Schuster)统计检验方法来检验它们是否与地球自转速率变化显著相关,检验的基本参数是(Schuster,1897).

(7)

式中,θi为第i个地震的相位角,N为地震总数.这里,N>10. 0≤P≤1,表示拒绝地震对于地球自转是随机发生的零假设的显著性水平,当P值越小时,表示排斥这一假设的置信度越高.一般地,如果P≤5%, 地震活动与地球自转之间存在显著相关性(Heaton,1975).

2 研究结果

2.1 2004年12月26日苏门答腊MW9.0地震

2.1.1b值

由于震区缺乏足够的分析视应力的资料,我们只能根据b值来分析构造应力的变化.分析中使用的地震目录来自于USGS网站 (https：∥earthquake.usgs.gov/ earthquakes/search/),选取了自1973年1月1日至2004年12月25日间发生的地震.这个地区地震目录完整性震级为MC=4.9(Chen et al., 2022).图1a、b分别为2004年12月26日—2005年1月31日M≥4.9余震震中以及1973年1月1日—2004年12月25日M≥4.9地震震中的空间分布.我们选择图1a 中黑色粗实线围成的多边形区域内发生的地震,以160个地震计算1个b值,在时间轴上以10个地震滑动,得到的b值随时间变化曲线(图1c).图中黑色粗实线为b值,灰色区域为按式(4)计算的b值的标准差.可以清楚地看到,在2004年苏门答腊MW9.0地震前b值存在长达10年左右的下降趋势变化, 从1.76降至1.12,相对降幅约36%,而在震前近4年的时间里一直保持在低位,且变化不大.

将纬度范围2°S—16°N和经度范围90°E—101°E所限定的区域分成0.1°×0.1°的网格,一共4949个.选取以网格节点为中心3°×3°的空间窗,当窗口内的地震个数Ne≥60时,选取50个地震计算b值,1个地震滑动,可以得到其b(t)曲线,然后根据式(5)计算在1990—1999年期间b值的相对降幅,将结果作为网格节点处的值.图1d中给出了b值相对降幅大于25%的空间分布.结果显示,2004年苏门答腊MW9.0地震前,在位于震中附近的一个不太大的区域内,b值下降幅度比其他地区都大.据此,可以推知,大地震发生前在震中附近地区的一个区域内,构造应力增加的幅度比其他地区大.

图1 (a) 2004年12月26日—2005年1月31日M≥4.9余震震中分布; (b) 1973年1月1日—2004年12月25日M≥4.9地震震中分布; (c) b 值随时间的变化(浅灰色区域为由式(4)得到的标准差范围); (d) b值下降幅度分布(下降幅度大于25%)“☆”为2004年12月26日苏门答腊MW9.0地震.黑色粗实线为全球板块边界(全文同).黑色虚线围成的多边形区域包含了余震区域,选取该区域内发生的地震计算b时间变化曲线.

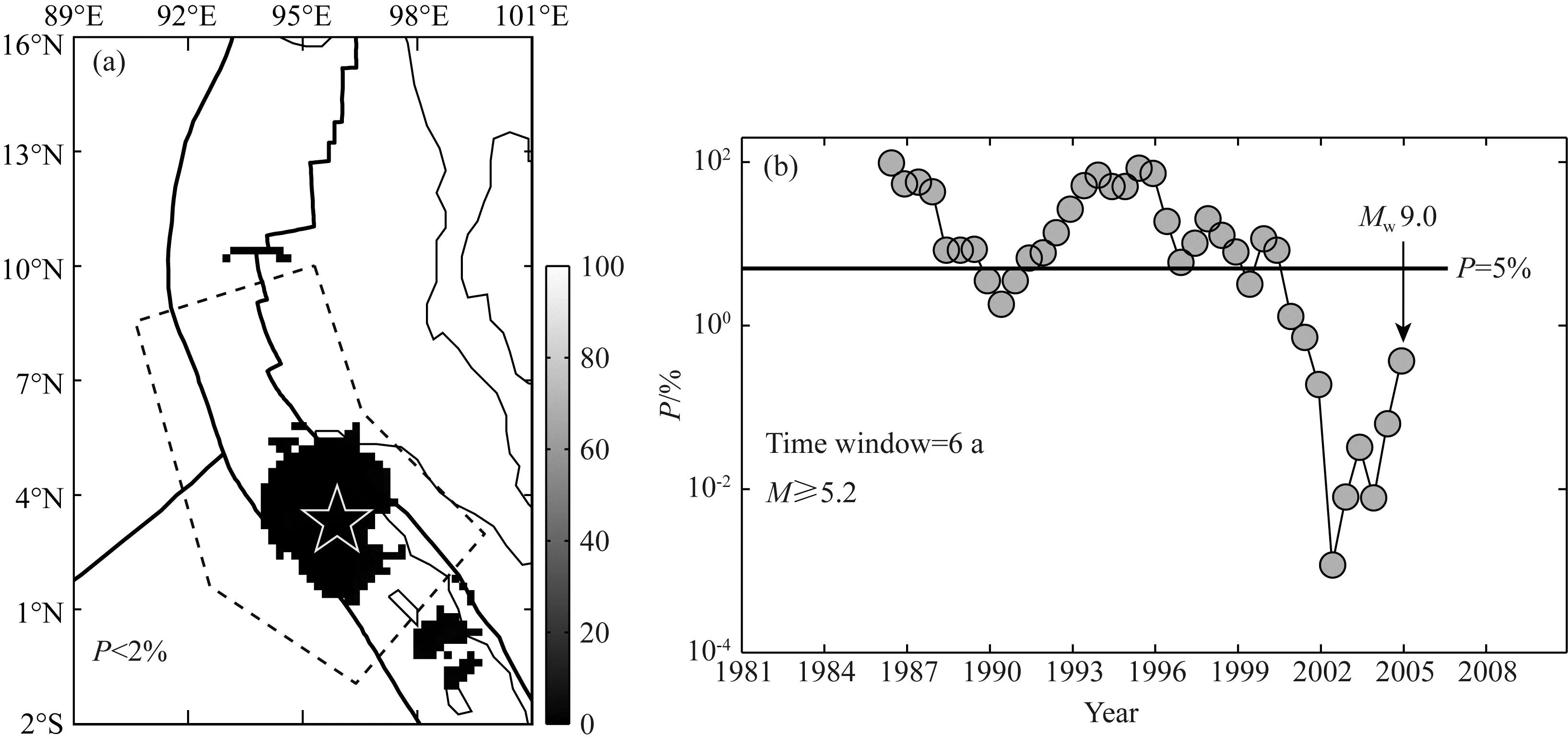
图2 (a) 低P值空间分布(P<2%); (b) P值随时间的变化(计算中运用了6年的时间窗,以6个月滑动)“☆”为2004年12月26日苏门答腊MW9.0地震.

2.1.2P值

利用1998年1月—2003年12月发生的M≥5.0地震的相位角,在经纬度范围为 (2S°—16°N, 89°E—101°E)的空间范围内,取半径为200 km的圆形区域为空间窗,对P值进行空间扫描可以得到P值空间分布.图2a中给出了低于2%的P值空间分布.可以看到,2004年苏门答腊MW9.0地震前低P值主要分布在震中附近地区.低P值意指地震活动与地球自转速率变化显著相关,地震活动受到地球自转速率变化的控制,反映了震中附近地区处于临界状态或亚失稳状态.利用比这个低P值区大一些的区域(图2a中黑色虚线围成的多边形区域)内于1980年1月至2004年11月间发生的M≥5.2地震的相位角计算了P值随时间的变化,计算中运用了6年的时间窗,以6个月滑动.结果表明P值从2000年初开始下降,于2002年5月达到0.0012%的最低值.从2001年至临近主震发生前P值低于1%(如图2b).

2.2 2010年2月27日智利Bio-Bío MW8.8地震

2.2.1 视应力和b值

从哈佛大学发布的震源参数目录(http：∥www.globalcmt.org/CMTsearch.html)中收集到2010年智利Bio-BíoMW8.8地震余震区内(图3a)1990年1月—2010年1月期间发生的5.0≤MW≤6.6地震,共计70次,以15次地震计算平均视应力,2个地震滑动,得到视应力随时间的变化(图3b).可以看出,视应力从2006年起呈显著上升趋势变化.

使用USGS地震目录,选取了自1990年1月至2010年1月间发生的地震.这个地区地震目录完整性震级为MC=3.7(Li et al., 2021).500个地震计算1个b值,在时间轴上以10个地震滑动,得到的b值随时间变化曲线如图3c.图中黑色粗实线为b值,灰色区域为b值的标准差.可以清楚地看到,在2010年智利Bio-BíoMW8.8地震前b值存在6年左右的下降趋势变化, 从1.87降至0.91,相对降幅约51%.在震前数年b值与视应力呈负相关关系,反映的是震区构造应力逐渐增强过程.

利用(40°S—29° S, 77° W—68°W)所限定的区域内的地震,将区域以0.2°×0.2°进行网格化.选取以网格节点为中心,半径为100 km的圆形空间窗,当窗口内的地震个数Ne≥208时,选取200个地震计算b值,2个地震滑动,可以得到其b(t)曲线,然后根据式(5)计算在2004年1月—2010年1月期间b值的相对降幅,可以得到b值相对降幅的空间分布.图3d中给出了b值相对降幅大于30%的空间分布.可以看到,2010年智利Bio-BíoMW8.8地震前,在破裂区北端及附近区域内,b值下降幅度比其他地区都大.在这个区域内构造应力增加的幅度比其他地区大.

2.2.2P值

利用2005年2月—2010年1月发生的4.7≤M≤5.9地震的相位角,在经纬度范围为 (28°S—44°S, 64°W—80°W)的空间范围内,取半径为220 km的圆形区域为空间窗,对P值进行空间扫描可以得到的P值空间分布.图4a中给出了P<2%的空间分布.可以看到,2010年智利Bio-BíoMW8.8地震前低P值分布在破裂区南部,震中位于P值区北边缘附近.利用图4a中黑色虚线围成的四边形区域内于2000年1月至2010年1月间发生的4.7≤M≤5.9地震的相位角计算了P值随时间的变化,计算中运用了5年的时间窗,以3个月滑动.结果表明P值从2000年初开始下降,于2009年7月下降到5%以下,临近地震前达到最低值0.34%(如图4b).

2.3 2011年3月11日日本本州 MW9.1地震

2.3.1 视应力和b值

视应力计算的数据来自于哈佛大学发布的震源参数目录.选取了1996年1月—2011年1月期间发生在图5a中蓝色实线围成的区域内的5.0≤MS≤6.9地震,共计99次,3年地震计算平均视应力,6个月滑动,得到视应力随时间的变化(图5b).可以看出,视应力从2000年起呈显著上升趋势变化.

图3 (a)2010年2月27日—2010年5月31日M≥5.0余震震中分布;(b)视应力随时间变化; (c) b 值随时间的变化(浅灰色区域为由式(4)得到的标准差范围); (d) b值下降幅度分布(下降幅度大于30%)“☆”为2010年2月27日智利Bio-Bío MW8.8地震.黑色粗虚线围成的区域大部分为余震区,选取该区域内发生的地震计算视应力和b值时间变化曲线.

图4 (a) P值空间分布(P<2%)(“☆”为2010年2月27日智利Bio-Bío MW8.8地震),(b)P值随时间的变化(计算中运用了5年的时间窗,以3个月滑动)

使用USGS地震目录,选取图5a中蓝色实线围成的区域内自1985年1月至2011年2月间发生的M≥4.9地震,共计973次.以300个地震计算1个b值,在时间轴上以5个地震滑动,得到的b值随时间变化曲线如图5c.图中黑色粗实线为b值,灰色区域为b值的标准差.可以清楚地看到,在2011年3月11日日本本州MW9.1地震前b值存在15年左右的下降趋势变化, 从1995年的约1.4降至2009年的约1.0,相对降幅约29%.b值与视应力呈负相关关系.

利用(31°N—42.5° N, 135° E—146°E)所限定的区域内的地震,将区域以0.2°×0.2°进行网格化.选取以网格节点为中心,3°×3°的矩形空间窗,当窗口内的地震个数Ne≥79时,选取70个地震计算b值,1个地震滑动,可以得到各网格节点处的b(t)曲线,然后根据式(5)计算在1995年1月—2009年12月期间b值的相对降幅,可以得到b值相对降幅的空间分布.图5d中给出了b值相对降幅大于30%的空间分布.可以看到,2011年日本本州MW9.1地震前,在震中西南部附近区域内,b值下降幅度比其他地区都大.即,在这个区域内构造应力增加的幅度比其他地区大.

2.3.2P值

利用2005年12月—2009年11月发生的5.3≤M≤6.9地震的相位角,在经纬度范围为(33°N—43°N, 138°E—147°E)的空间范围内,取2.5°×2.5°的矩形区域为空间窗,对P值进行空间扫描可以得到P值空间分布.图6a中给出了P<2%的空间分布.可以看到,2011年日本本州MW9.1地震前低P值分布在震中附近.利用图6a中黑色虚线围成的四边形区域内于1991年1月至2011年2月间发生的5.3≤M≤6.9地震的相位角计算了P值随时间的变化,计算中运用了4年的时间窗,以3个月滑动.结果表明P值大约在2009年8月下降至5%以下,于2010年2月达到最低值0.06%(如图6b).

3 结论与讨论

根据上述三次MW9.0级左右地震前震源及其附近地区视应力、b值和P值分析,发现：

(1) 震前构造应力存在明显的增强过程,持续时间在数年至10年以上;

(2) 在b值下降期间,较大的b值下降幅值分布在破裂区内,表明强震的孕育可能与应力增强幅度有关;

(3) 临近地震发生前几年,地震活动与地球自转之间显示出显著的相关性,在震中及邻近地区,与地球自转相关的地震活动性最为显著.

根据上述结果,我们可以得出如下结论：震前震源及附近地区地壳构造应力有显著增强过程,在临近地震发生前几年内,震源区进入亚失稳状态,变得极不稳定,地震活动受到地球自转速率变化的控制.因此,从这三个震例的结果来看,地震孕育过程与岩石力学实验结果具有一致性.我们也分析了其他几次7～8级左右地震的孕育过程,与前述3次地震相比,尽管它们所处的地质构造背景具有较大的差异,但也得到了类似的结果(图7—8).这些震例分别是：1976年7月28日河北唐山MS7.8地震、2008年5月12日四川汶川MS8.0地震、2019年7月6日美国加州RidgecrestMW7.1地震以及2021年7月29日美国AlaskaMW8.2地震.由于资料问题,前3次震例只能给出b值分析结果.

本文对三次MW9左右地震的孕震过程进行了系统分析,同时也给出了其他一些震例结果.总的来说,强震发生前,在震中及其附近地区存在显著的应力增长过程,在震前4年左右的时间内地震活动受到地球自转速率变化的控制,显示出亚失稳或临界状态的特征,与岩石力学实验所得到的结果具有一致性.用实际地震资料验证了天然地震孕育过程与岩石实验中岩石破坏前所经历的过程是一致的.这不仅对利用岩石力学实验更加深入研究地震孕育过程及利用实验结果指导地震预测研究具有现实意义,同时对实际地震震情判定也具有重要意义.本研究不仅揭示了强震孕育过程特征,而且也发展了追踪孕震过程的方法,即联合利用视应力和b值约束构造应力的变化,利用地震活动与地球自转的相关性分析临界状态,由此可以给出一个地区孕震过程所处的阶段特征,进而对地震发生的紧迫性进行评估.如果将非测震学前兆(也称地球物理观测前兆)与孕震过程相结合,可以显著提高对非测震学前兆的识别以及加深其与强震发生的关联性的认识.对提高实际地震预报工作质量具有重要意义.

图5 (a) 2011年3月11日—2011年5月31日M≥5.5余震震中分布; (b) 视应力随时间变化; (c) b 值随时间的变化(浅灰色区域为由式(4)得到的标准差范围); (d) b值下降幅度空间分布(下降幅度大于30%)“☆”为2011年3月11日日本本州 MW9.1地震.选取黑色虚线围成的区域内发生的地震计算视应力和b值时间变化曲线.

图6 P值空间分布(P<2%)(a);P值随时间的变化(b)“☆”为2011年3月11日日本本州 MW9.1地震.图b计算中运用了4年的时间窗,以3个月滑动.

图7 b值下降幅度空间分布(a1—d1), 视应力和b值随时间变化(a2—d3)浅灰色区域为b值标准差范围.a1—a2：1976年唐山MS7.8地震. a1为1973年1月—1975年12月间b值下降幅度空间分布(下降幅度大于20%).红色实线围成的区域内发生的ML≥1.5地震用于计算b值随时间的变化.a2 为b值随时间的变化(100个地震计算,5个地震滑动).b1—b2：2008年汶川MS8.0地震.b1为2002年1月—2008年4月间b值下降幅度空间分布(下降幅度大于25%).红色实线围成的区域内发生的ML≥1.5地震用于计算b值随时间的变化.b2 为b值随时间的变化(600个地震计算,10个地震滑动).c1—c2：2019年美国加州 Ridgecrest MW7.1地震.c1为2002年1月—2009年12月间b值下降幅度空间分布(下降幅度大于35%).红色虚线围成的区域内发生的M≥1.8地震用于计算b值随时间的变化.c2 为b值随时间的变化(1500个地震计算,10个地震滑动).d1—d3： 2021年美国 Alaska MW8.2地震.d1为2010年1月—2018年12月间b值下降幅度空间分布(下降幅度大于20%).黑色四边形区域内发生的M≥3.0地震用于计算b值随时间的变化.d3为b值随时间的变化(500个地震计算,3个地震滑动).

续图8