多连通区域到狭缝圆环域的共形映射计算法
赵 鑫, 吕毅斌
(昆明理工大学 理学院, 昆明 650500)
0 引 言
共形映射可将复杂区域映射到正则狭缝域,同时保持曲线之间的夹角在大小和方向上不变,这一性质常用于复杂区域中研究的问题,例如应用于流体力学、水波和弹性力学等领域内的许多实际问题[1-7].但是,将复杂区域共形映射到正则狭缝域的解析式难以求得,针对这一问题,许多研究者以计算机为工具,提出了有效的数值方法和思想[8-19].例如:1966年,Symm[8-10]首次使用计算机计算了共形映射的数值解,该方法利用位势理论提出了使用第一类Fredholm积分方程,计算了单连通区域和双连通区域的数值共形映射映射函数.1988年,Amano[11]简化了Symm的方法,提出了基于模拟电荷法的数值共形映射计算法(Amano法),用于将任意单连通区域共形映射到单位圆盘.后经不断发展,其也可用于计算多连通区域到多种正则域的共形映射函数[12-15].2009年,Nasser等[16-17]将求解共形映射函数的问题转化为求解一个Riemann-Hilbert问题,提出了带广义Neumann核的第二类Fredholm积分方程法,并将其应用于碳纳米管增强复合材料内稳态热传导的仿真模拟.
1916年,Koebe[20]提出了39种具有广泛应用前景的正则狭缝域,并将其归为5类.目前,虽然存在许多计算多连通区域共形映射的数值方法,但是其研究内容大都针对于将低连通度区域共形映射到较为简单的第一类正则狭缝域[14-16,21-25].区域的连通度以及正则狭缝域复杂度的提高会导致共形映射的计算量和误差大大增加,而模拟电荷法在计算共形映射的过程中不计算数值积分,并且使用最大模原理评价误差,所以具有计算时间短、计算精度高、避免计算奇异积分等优势.因此,本文基于模拟电荷法,研究了将有界高连通度区域映射到更为复杂的,对数螺旋狭缝单位圆环[26]的共形映射计算法.首先,我们给出了正规化条件和共形映射的函数形式,并使用Laplace方程基本解的线性组合近似函数形式中的待定函数.其次,根据Dirichlet边界条件建立未知量应满足的约束方程组,并提出利用BiCR算法[27]求解病态约束方程组,得到模拟电荷,进而构造出高精度的近似共形映射函数.最后,在数值实验中,通过对有界10连通区域和有界16连通区域进行数值实验,验证了本文算法的有效性,并模拟了有界高连通度区域内螺旋点涡的绕流.
本文主要部分结构如下:第1节给出了将有界高连通度区域映射到对数螺旋狭缝单位圆环(S)的共形映射函数与调和函数(a(z))的近似形式,并根据边界条件构造出约束方程组.第2节提出了利用BiCR算法计算约束方程的矩阵形式,得到了精度更高的模拟电荷.第3节简述了将本文共形映射计算法应用于绕流模拟的原理.第4节通过数值实验验证了该算法的有效性,并给出了有界高连通度区域内螺旋点涡的绕流仿真结果.第5节对全文进行了总结和展望.
1 有界高连通度区域到对数螺旋狭缝单位圆环域的共形映射
1.1 共形映射函数及边界条件
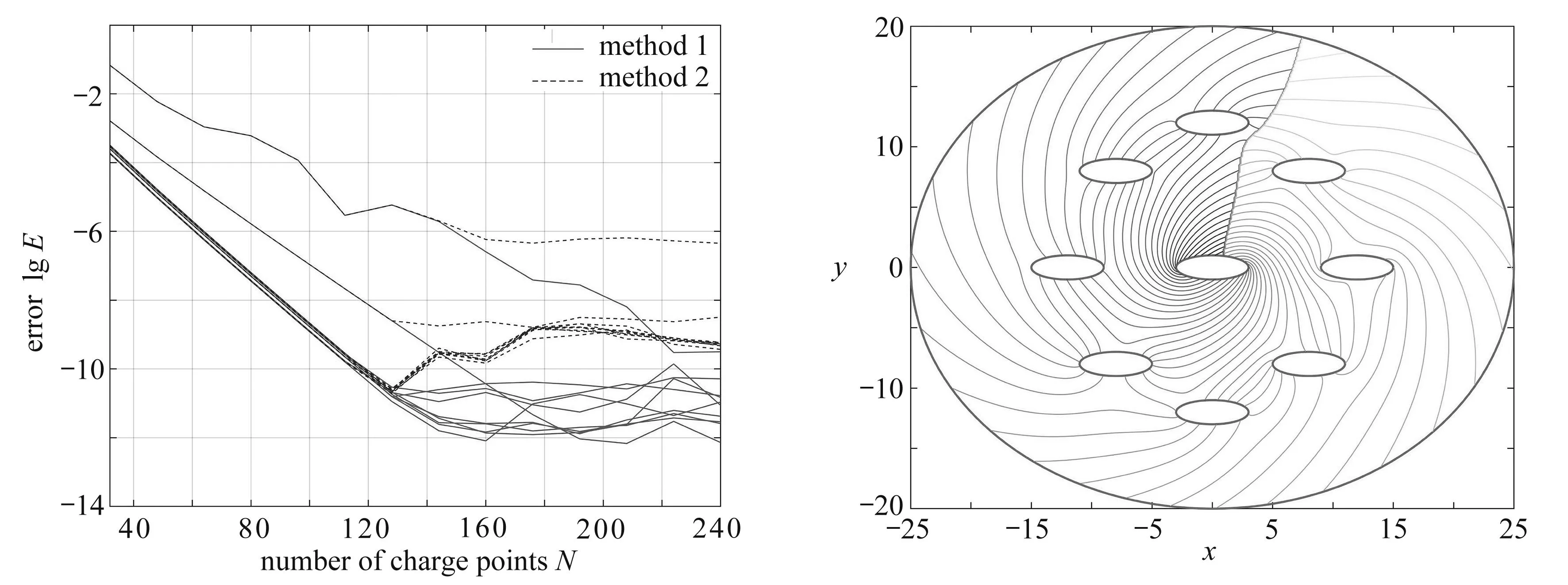
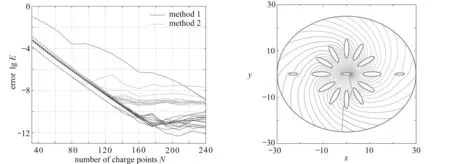
在z平面上,区域D是一个连通度为n(≥10)的有界高连通度区域,其边界∂D=C由n条封闭的Jordan曲线C1,C2,…,Cn组成,即C=C1∪C2∪…∪Cn.共形映射函数w=f(z)将曲线C1映射到单位圆|w|=R1=1,将曲线C2映射到圆盘|w|=R2,将曲线Cm映射到单位圆环内斜角为θm的对数螺旋狭缝Sm(m=3,4,…,n),见图1,图中“·”代表约束点,“+”代表模拟电荷点(后同).斜角是指对数螺旋狭缝与从坐标系原点发出的射线相交所形成的夹角,始终是一个固定值θ.值得注意的是, 当斜角θ=0和θ=π/2时, 对数螺旋狭缝将分别退化为从原点发出的射线和以原点为圆心的圆弧.综上所述, 共形映射函数w=f(z)的边界值应满足
(1)
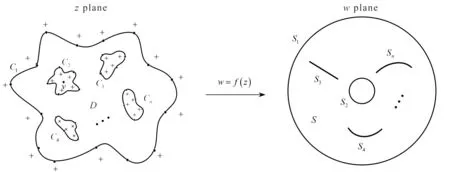
图1 基于模拟电荷法的有界高连通度区域共形映射Fig. 1 Conformal mappings of bounded high connectivity regions based on the charge simulation method
其中,z∈Cm;R2,…,Rn为待定实常数;θ1=θ2=π/2,θ3,…,θn为给定实常数.
对于有界多连通区域D,满足正规化条件f(0)>0的共形映射函数w=f(z)是唯一确定的,函数形式可定义为
(2)
其中,c=f(0)为正实常数,v是边界C2内侧一定点,将式(2)代入式(1),得
z∈Cm,m=1,2,…,n.
(3)
1.2 模拟电荷法的原理
根据模拟电荷法的原理,a(z)可由Laplace方程基本解的线性组合近似,即
(4)
其中,Q0为未知复常数,电荷Qlj为待定实数,ζlj是配置在曲线Cl外的模拟电荷点,见图1.为了将有界多连通区域映射到区域S,式(2)需满足以下条件[15]:
即
(5)
② 保持近似函数在问题区域D上的坐标系放缩不变性[15,28],有
(6)
③ 正规化条件,由f(0)=c可得
(7)
结合式(4),消去Q0,可得到
(8)
(9)
即可保证A(z)在区域D中连续,进而能够在问题区域上构造一个连续的近似映射函数.
根据上述条件①、②和③,通过限制近似函数(9)中的z取Cm上的约束点zmk,令其满足边界条件(1),则可得到关于电荷Qlj和Hm满足的N1+N2+…+Nn+n维约束方程组,即
zmk∈Cm;m=1,2,…,n;k=1,2,…,Nm.
(10)
将求得的电荷Qlj代入式(9),可解得a(z)的近似函数A(z).随后将A(z)代入式(2),便可得到共形映射函数f(z)的近似函数,记为F(z).
2 求解模拟电荷的BiCR法
现将约束方程组(10)写成标准线性方程组Ax=b的形式:
A∈(N1+N2+…+Nn+n)×(N1+N2+…+Nn+n),x∈(N1+N2+…+Nn+n),b∈(N1+N2+…+Nn+n),
其中,A是非对称的,Nm(1,2,…,n)表示每条边界上的模拟电荷点数.
在基于模拟电荷法的共形映射计算法中,线性方程组的求解精度对最终的映射结果起着关键性作用.数值共形映射的精度要求越高,所取的模拟电荷点数就需要越多,但线性方程组的系数矩阵随着模拟电荷点数的增加,条件数cond(A)也随之增大.所以,针对病态矩阵A,本文使用BiCR算法求解线性方程组.BiCR算法是由Sogabe在conjugate residual(CR)算法的基础上提出的,可以高效求解非对称线性方程组,从而提高所求模拟电荷的精度,进而能够得到高精度的近似共形映射函数.求解模拟电荷的BiCR法标准步骤如下.
算法1 求解模拟电荷的BiCR法
1 输入A,b,x0,ε,nmax
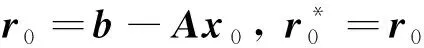
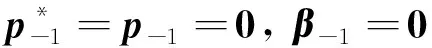
4 forn=0,1,2,…
5 if |rn|>ε,n 6pn=rn+βn-1pn-1; 9xn+1=xn+αnpn; 10rn+1=rn-αnApn; 13 else break; end if 14 end for 15 输出xn+1. 上述算法中,x0是给定的初始近似值,取值为零向量,r0=b-Ax0是初始向量,ε是给定误差,nmax为最大迭代次数. 在流体力学领域中,绕流是指绕过置于无限流体中的物体的流动,或物体无限流体中运动,是自然界和工程中常见的黏性流体运动形式.其在能源动力工程、海洋工程和航空航天工程等领域中具有重要意义[29-31].通过使用共形映射将复杂的多连通区域映射为简单的正则狭缝域后,根据问题域内的复势可以由正则域上的复势经过共形映射得到,可计算出平面无旋流在有界多连通区域内各点的复势,进而模拟出该平面无旋流的流线和等势线.使用共形映射计算多连通区域内的复势的原理如下: 设D(z)=φ(x,y)+iψ(x,y)和S(w)分别是区域D和区域S内的复势,其中φ表示速度势,ψ表示流函数.共形映射函数w=f(z)将区域D映射到区域S,同时也将区域D内的流线族映射到区域S内的流线上.原因是定义在区域D内的调和函数经过共形映射后仍是调和函数,因此,当S(w)已知时,区域D内的复势可表示为 S(w)=S(f(z))=D(z),z∈D. (11) 在MATLAB 2018b的环境下,对连通度为n(≥10)的有界高连通度区域共形映射到对数螺旋狭缝单位圆环进行数值实验,检验本文算法的有效性和精度.共形映射误差由 (12) 步骤1 设定正整数Nl,实常数θ1=π/2,θ2=π/2,θ3,…,θn,合适的模拟电荷点ζlj(l=1,2,…,n;j=1,2,…,Nl)与对应数量的约束点zmk(m=1,2,…,n;k=1,2,…,Nm),边界Cl内侧的相应定点ζl0(l=1,2,…,n)和v. 步骤2 将ζlj,zmk,ζl0代入式(10),得到将有界高阶连通区域映射到区域S的约束方程组,求解约束方程组,得到实常数Hl、正实常数c和电荷Qlj. 在步骤2求解约束方程组时,本文使用BiCR算法进行求解,并与同是迭代法的GMRES(m)(the generalized minimal residual)算法[12,34]进行比较,将前者记为method 1,后者记为method 2.广义极小残差法GMRES(m)是在Krylov子空间讨论求解线性方程组的方法,可以直接应用于求解系数矩阵密集且不对称的大型线性方程组. 例1 将z平面上的有界10连通区域(图2)共形映射到w平面上具有8条对数螺旋狭缝的单位圆环(图3).给定图3中对数螺旋狭缝的斜角为 图2 有界10连通区域网格图 图3 带有对数螺旋狭缝的单位圆环 Fig. 2 The grid diagram of bounded 10 connected domains Fig. 3 The unit circular ring with logarithmic spiral slits 图4 例1中共形映射误差曲线 图5 例1中螺旋点涡的绕流模拟 Fig. 4 The conformal mapping error curves in example 1 Fig. 5 Simulation of flow over the spiral point vortex in example 1 图6 有界16连通区域网格图 图7 带有对数螺旋狭缝的单位圆环 Fig. 6 The grid diagram of bounded 16 connected domains Fig. 7 The unit circular ring with logarithmic spiral slits 图8 例2中共形映射误差曲线 图9 例2中螺旋点涡的绕流模拟 Fig. 8 The conformal mapping errors curves in example 2 Fig. 9 Simulation of flow over the spiral point vortex in example 2 本文基于模拟电荷法,提出了将有界高连通度区域映射到对数螺旋狭缝单位圆环的共形映射计算法,模拟了有界高连通度区域内螺旋点涡的绕流.在约束方程组的求解中,本文提出利用BiCR算法构造高精度的共形映射函数,得到了比基于GMRES(m)算法改进的共形映射计算法更好的新算法,即基于BiCR算法改进的共形映射计算法,并通过数值实验验证了本文算法的有效性.在今后的研究中,我们将继续研究具有广泛应用前景的正则狭缝域,其次我们也会将共形映射用于求解热传导和图像处理等领域的实际问题.3 螺旋点涡的绕流模拟
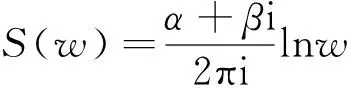
4 数 值 实 验
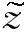




5 结 论

