基于KPCA+LR的电力现货市场发电企业串谋行为分析

高丽杰 华回春

（华北电力大学）

0 引言

在电力市场的发展过程中，达到资源的优化配置以及保障电力供应安全是市场建设的主要目标。我国各地区资源差异性和互补性较大[1]，省间电力资源调剂余缺需求很大，迫切需要建立完善的省间电力现货市场来保障供应。在省间现货市场建设初期，由于市场制度的不完善，会出现市场成员滥用市场力的问题，市场力是指发电商改变市场价格并使之偏离市场充分竞争情况下的价格水平的能力。

滥用市场力会降低市场效率，损害用户利益，妨碍市场健康稳定运行。2000年美国加州出现电力危机，发电商行使市场力使得市场价格飙升，导致诸多公司负债累累并处于破产状态[2]，损害了用户以及投资人的利益。在我国的电力市场建设过程中，一些市场主体为了谋得暴利采用串谋的方式进行违规报价，严重影响市场发电价格的能力，存在部分发电公司故意减产并试图抬高价格的行为，而合理的价格以及可靠的电力供应对电力市场的健康发展尤为重要，我国的省间电力现货市场正在初步建设当中，所以对市场进行有效监管以促进公平竞争迫在眉睫。

目前诸多学者进行了对电力市场串谋行为识别的研究，文献[3]通过对电力市场运营大数据进行分析，建立了完善的风险评估体系。文献[4]从市场结构、市场供需等多个方面构建了市场力评价指标体系。

文献[5]提出基于物理潮流分析的市场力评价指标体系，能够反映机组地理位置以及电网约束对市场力行使的影响。文献[6]构建了博弈论模型，从机理角度分析串谋，利用均衡模型分析市场主体的战略行为是电力市场领域的研究热点[7]，但是模型的假设通常不符合电力市场的实际运行条件，在实际中应用价值不高。文献[8]提出基于云模型和模糊Petri网的串谋识别方法，但是随着交易数额增大，数据样本增多会导致该方法的计算量过大。文献[9]考虑到我国电力现货市场运行时间不长，带标签的数据少，提出使用半监督支持向量机算法训练可靠分类器。文献[10]提出基于AdaBoost-DT算法的串谋行为智能识别方法，实时性和准确性较好。文献[11]提出了基于模糊集理论和层次分析法的电力市场综合评价方法，该方法既可以从整体上把握市场发展趋势，又可以反映市场组成的微观情况，能够为决策者提供建议。

考虑到省间电力现货市场仍旧处于初步建设阶段，发电企业之间的串谋行为影响资源优化配置并且可能对市场造成破坏，为规避风险并且确保电力市场健康稳定运行，本文设计了KPCA+LR模型进行发电企业串谋行为识别，此方法可避免数据维度过高导致模型过拟合的问题，而且准确率较高，有很高的实用价值。

1 发电企业串谋行为识别指标体系

串谋是发生在两个及以上的发电企业之间的行为，为了准确评估发电企业的行为，本文从五个方面构建了基于任意两个发电企业的串谋行为识别指标体系。

（1）市场份额

该指标是指任意两个发电企业的申报电量占所有发电企业申报电量的比例，具体表示如下：

式中，qi和qj为发电企业i和j的申报电量；N是指一共有N家发电企业参与此次竞价。市场份额越高，代表发电企业有更大的操纵市场的能力，发生串谋行为的可能性越大。

（2）持留比率

该指标反映任意两家发电企业对电量供应的控制程度，具体表示如下：

式中，Qi和Qj表示发电企业i和j的可发电容量，持留比率越高则说明发电企业限制容量并且提高市场价格的可能性越大，那么发生串谋的可能性也就越大。

（3）中标率

该指标表示发电企业i和j的中标电量与申报电量的比值，具体表示如下：

（4）高价中标率

该指标表示任意两家发电企业报高价中标的电量占中标电量的比率，具体表示如下：

式中，Qhi和Qhj表示发电企业i和j报高价且中标的电量，该指标值越大说明这两家企业发生串谋的可能性越大。

（5）报价相对比均值

2 基于KPCA+LR的电力市场发电企业串谋识别模型

将串谋识别问题视作二分类问题，由于串谋识别模型所用数据集具有高维特性，综合考虑模型的复杂度以及分类的准确率等因素，采用核主成分分析法结合逻辑回归算法构建发电企业串谋识别模型。

2.1 KPCA+LR模型

逻辑回归算法（Logistic Regression，LR）是一种假设样本数据服从伯努利分布，利用极大似然估计和梯度下降求解的用作分类的机器学习算法，是广义线性回归分析模型，训练速度快而且可解释性强。模型使用sigmoid函数将预测范围从实数域压缩到（0,1）范围之内从而提高模型的准确率，函数图像如图1所示，函数公式如式（6）所示：

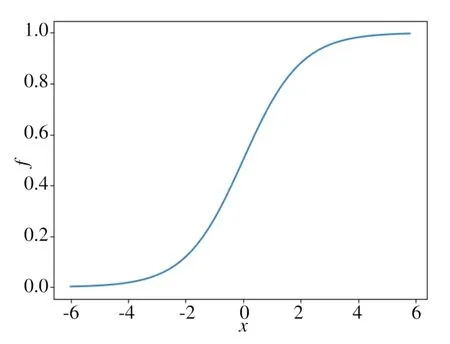
图1 sigmoid函数

f(x)表示样本为类别1的概率，x为线性函数，表达式为x=wTu+b，其中，w和b均为参数矩阵，u为输入的特征向量，样本被预测为正例和负例的概率表达式如式（7）所示：

y有两个取值，分别为0和1，y=1表示样本被预测为正样本，y=0表示样本被预测为负样本。为避免陷入局部最优解，逻辑回归的损失函数采用对数损失函数，如式（8）所示：

式中，n为样本数量。

高维特征数据增加了计算的要求，使得数据分析变得复杂，导致模型复杂度增加，易导致过拟合问题。把数据降维在一定的信息损失范围之内能最大限度反映原始数据中的有用信息，可消除一些噪声和误差，并且帮助节省大量时间成本。针对这一问题，本文使用核主成分分析（Kernel Principal Component Analysis，KPCA）对数据进行降维处理。KPCA利用非线性变换将原数据映射到高维空间中进行主成分分析的数据处理，再将主成分映射回原来的空间当中，得到降维之后的数据。针对本文所提问题，考虑到数据具有高维特征，先使用KPCA对数据进行降维处理，再通过逻辑回归算法实现发电企业的串谋行为识别，模型具体算法如下。

（1）输入

含标签的数据集U：

（2）输出

二分类结果：

1）对输入样本进行中心化；

2）利用核函数计算核矩阵；

3）计算核矩阵的特征值和特征向量；

4）将特征向量按对应特征值从大到小排列，取前3列数据作为降维后的数据；

5）载入降维后的数据，使用sigmoid函数进行计算；

6）更新权值。

2.2 实验分析

以中国某地区省间电力现货市场交易数据为例进行分析，应用本文方法对其进行发电企业串谋行为识别分析，验证本文所提出方法的有效性。基于KPCA+LR的串谋识别模型流程如图2所示。

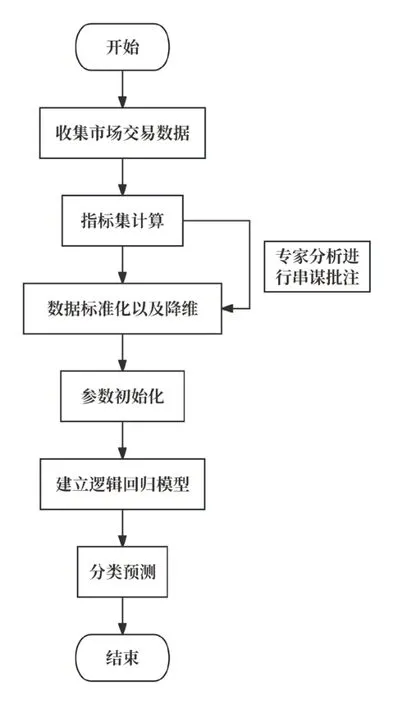
图2 基于KPCA+LR的串谋识别模型流程

结合文中建立的指标体系，计算任意两家发电企业的串谋行为识别指标数据，指标数据样本总计3655个，部分指标数据集展示如表1所示，标签值为1代表该样本为串谋样本，标签值为0代表该样本为正常样本。

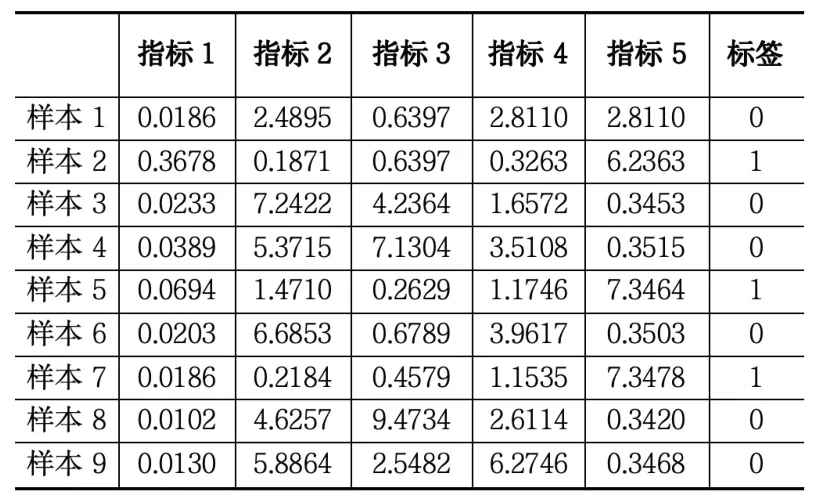
表1 部分指标数据集

将指标集数据进行可视化，如图3所示。由于指标集为六维数据，普通的三维空间不能完整刻画数据信息，所以在本研究中使用三个常规轴以及大小、形状、颜色来可视化六维数据。前三个指标用常规轴表示，指标4用图中散点形状的大小衡量，数值越大则形状越大。指标5由散点形状表示，数值大于6则很大几率为串谋情况，因此如果值大于6，那么散点形状为三角形，否则散点形状为圆形。红色代表正常样本，蓝色代表串谋样本。由图3可知，原始指标数据的串谋样本与正常样本分布位置难以区分，且正常样本的个数远多于串谋样本的个数。

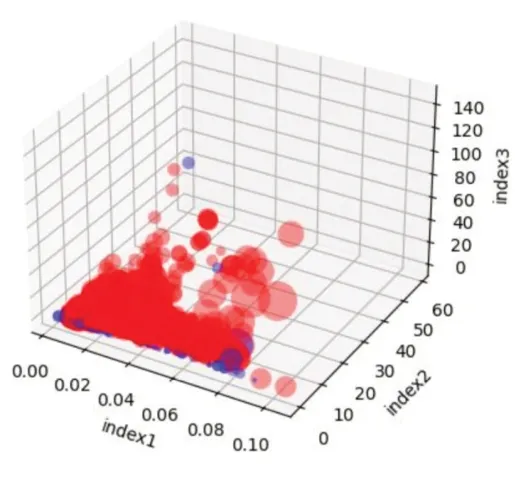
图3 原始指标数据散点图

利用KPCA进行数据降维处理，将原始六维数据降维至三维，降维数据如图4所示，红色和蓝色分别代表正常样本和串谋样本。与图3相比，图4中的串谋样本和正常样本分布位置能够直观判断，发现大部分的串谋样本集中在某一区域，与正常样本有明显的位置区分。

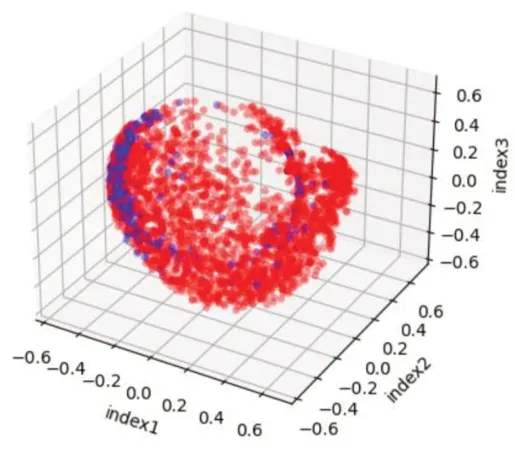
图4 KPCA降维之后的指标数据散点图

对降维后的指标数据集进行排序并进行划分，70%的数据作为训练集，30%的数据作为测试集。

接受者操作特性曲线（Receiver Operating Characteristic Curve，ROC曲线）是以假阳性率为横轴，真阳性率为纵轴构成的坐标曲线。AUC（Area Under Curve）是指ROC曲线与横坐标轴围成的面积，取值范围在0.5和1.0之间，越接近1.0，说明方法的应用价值越高。图5为本文模型的ROC曲线图，AUC值为0.85，可见模型的分类效果较好，有较高的应用价值。

图5 接受者操作特性曲线

用混淆矩阵展示本文所提模型的预测效果，如表2所示，负样本即为串谋样本。

表2 KPCA+LR模型的混淆矩阵

准确率表示被预测为正样本的数量与总样本数量的比值，精确率表示真正为正类的样本数量与模型将样本识别为正类的样本数量的比值，具体计算公式如式（10）和式（11）：

式中，V1为正样本被预测为正样本的数量；V2为负样本被预测为正样本的数量；V3为正样本被预测为负样本的数量；V4为负样本被预测为负样本的数量。

采用一种有监督模型SVM（Support Vector Machine）与一种无监督模型LOF（Local Outlier Factor）与本文模型进行比较，如表3所示，KPCA+LR可有效检测样本的异常状况。虽然LOF在训练过程中不需要带有标签的数据，但是准确率和精确率远低于本文模型，具有更高的工程实用价值。

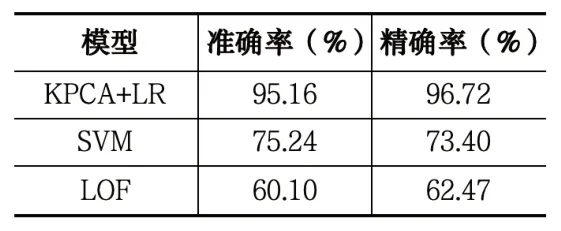
表3 不同模型的串谋识别准确率和精确率

3 结束语

针对省间现货市场发电企业串谋行为监测问题，本文构建了较全面的适用于中国电力市场的指标体系，提出了KPCA+LR算法。数据维度越高导致模型的复杂度越高，易导致过拟合现象，针对此问题，本研究提出使用核主成分分析方法进行数据降维处理。本文所提方法能够基于电力交易数据实现对发电企业串谋行为的精准识别，降低市场风险，串谋行为不仅发生于发电企业之间，售电公司以及用户也会存在一些串谋行为，针对不同主体之间的串谋行为识别问题此方法依旧适用。所提模型能够为市场监管者提供有力的帮助，有助于电力市场的公平稳定发展。