PCL/ASA药物控释系统结构拓扑优化及瞬态释药性能

高扬，孟繁舒，闵浩楠，剌焕军，陈磊，后振中

(1.西安科技大学机械工程学院，西安 710054； 2.西安交通大学机械制造系统工程国家重点实验室，西安 710049；3.西安科技大学材料科学与工程学院，西安 710054)

拓扑优化是一种在给定设计域内获得最佳材料分布的结构设计方法，通过寻找材料的最优分布，使结构的目标性能在约束条件下达到最优状态[1]，为设计者提供最有效的解决方案。由于拓扑优化具有非常高的设计自由度，目前已经被广泛应用于结构力学[2]、传热学[3]及光子学[4]等领域。在医工结合背景下，拓扑优化已被应用于腰椎融合器设计[5]、颌骨重建骨板[6]和牙种植体[7]等，然而，拓扑优化应用于药物控释系统的结构设计相对较少。

精准医疗[8]是一种基于患者病情的“定制”医疗模式，可以为患者提供个性化的治疗方案[9]，最终达到治疗效果精准化和患者受益最大化。药物的精准控释是精准医疗的一个重要组成部分，药物控释系统应运而生并迅速成为医药领域的研究热点，尤其是在慢性疾病的长期治疗过程中，药物控释系统可以植入病灶附近，控制药物在靶向部位按照需求的速率长期释放[10-11]。药物控释系统具有持续、稳定和低副作用等优势，同时通过对其进行结构设计，如多层结构[12]、微球[13]和微孔储库结构[14-15]等方式，可以实现药物的控制释放。

药物控释系统中常用的载体材料有聚己内酯(PCL)[16]、明胶[17]、壳聚糖[18]、聚乳酸(PLA)[19]和聚乳酸-羟基乙酸共聚物(PLGA)[20]等。其中，PCL具有良好的生物相容性和生物降解性，已被广泛应用于药物载体[21]和组织工程支架[22]等领域。阿司匹林(ASA)作为一种临床使用近百年的药物，在慢性肾脏病等慢性疾病的治疗中有较好的治疗效果[23]。但是，口服的ASA在经过体液循环后，作用时间较短，释药持续性不高，若设计一种载有ASA的药物控释系统，实现该药物的长期按需释放，则可为慢性疾病的治疗提供一种新的解决方案。

笔者首先基于质量传递方程建立了PCL/ASA药物控释系统的释药模型及拓扑优化模型。以设计域平均浓度与目标浓度之差的最小值作为优化目标，根据不同目标浓度设计出满足要求的PCL/ASA药物控释系统拓扑优化结构，实现针对不同用药需求的参数化结构设计。其次，对不同目标浓度对应的拓扑优化模型进行几何重构，研究了瞬态下储库形状和流道结构对释药能力的影响。最后通过体外释药实验验证了该优化方法和模型的合理性。

1 材料与方法

1.1 主要原材料

PCL：相对分子质量为30 000，熔融温度为60～63 ℃，瑞典Perstorp公司；

ASA：分子式为C9H8O4，纯度为98%，分子量为180.16，上海国药集团化学试剂有限公司。

1.2 仪器及设备

紫外-可见分光光度(UV-Vis)计：UV-3600，岛津(上海)实验器材有限公司；

真空干燥箱：DZF，北京市永光明医疗仪器有限公司；

电子分析天平：SQP，赛多利斯科学仪器(北京)有限公司；

电火花数控线切割机床：DK7750，江苏冬庆数控机床有限公司。

1.3 试样制备

采用模压成型法来加工制造PCL/ASA药物控释载体。模具的型芯采用电火花数控线切割工艺进行加工，设备参数设置如下：脉冲宽度为8，脉冲间隙为9。利用制备好的模具完成PCL/ASA药物控释载体的制备：首先对材料进行预处理，将足量的PCL颗粒放置于烧杯中并在30 ℃真空干燥箱中做干燥处理，待其干燥水分至恒重后取出并密封保存；将预备好的PCL颗粒填充于模具中，将其放置于70 ℃的真空干燥箱中熔融并进行真空脱泡；待模具中的PCL颗粒全部熔融且无气泡时，将模具盖板安装好并使用砝码将其压住，然后放置在30 ℃的真空干燥箱中定型2 h左右；最后将定型的载体进行脱模并放置于密封袋中备用。

1.4 PCL/ASA药物控释系统拓扑优化模型

优化前的PCL/ASA药物控释系统的二维模型如图1所示。该药物控释系统由药物储库Ω1和设计域Ω2两部分组成。Ω1中的药物通过Ω2从药物扩散边界θ3扩散到外界(θ1为药物储库边界、θ2为无通量边界)。其中，药物载体长度l1为10 mm，药物载体宽度l2为5 mm，药物储库长度l3为3 mm，药物储库宽度l4为1.5 mm，扩散边界间距l5为2 mm，扩散边界长度l6为1 mm。

对PCL/ASA药物控释系统中药物传质过程做如下假设：

(1)为了尽可能模拟临床环境，假设整个优化过程均在37 ℃的温度下进行，设计域的初始药物浓度为0 mol/m3；

(2)由于PCL降解周期较长，因此忽略其降解特性对释药性能的影响；

(3)在优化过程中，药物释放仅受浓度梯度下扩散机理的控制，且释药过程中不发生溶胀、对流和收缩等现象；

(4)在PCL内不发生化学反应，也没有新的药物生成。

基于上述假设，药物控释系统的药物传质满足菲克第二扩散定律。PCL/ASA药物控释系统释药模型的边界和初始条件设如下。

(1)药物储库边界θ1：在药物传递过程中，假设药物储库可以持续向外释放ASA，储库边界浓度始终为ASA在体液中的饱和浓度55.51 mol/m3。

(2)无通量边界θ2：在药物传递过程中，ASA不通过θ2扩散至外部。

(3)药物扩散边界θ3：在药物传递过程中，ASA仅通过θ3扩散至外界，由于外部环境模拟体液循环状态，假如药物通过θ3扩散到外界会被循环体液带走，故假设药物扩散边界的浓度始终为0 mol/m3。

(4)根据浓度梯度法[24]测得ASA在PCL中的扩散系数Dmin为6.12×10-11m2/s，在生理盐水中的扩散系数Dmax为1.13×10-9m2/s。

用拓扑优化方法对PCL/ASA药物控释系统进行结构设计时，将伪密度值作为设计变量，用其建立设计变量和载体材料之间的关系，其取值范围为[0，1]。其中，0表示PCL载体，1表示流道。在优化过程中，设计域被划分为网格，每个网格可以取不同的伪密度值。具体优化模型见式(1)。

式中：γ为设计变量；qv为体积约束因子；γmin为γ最小值，为了防止在计算过程中发生矩阵奇异，取γmin为0.001；V为设计域的初始体积。

在恒定的边界和初始条件下，PCL/ASA药物控释系统的累积释药量可由设计域中的药物平均浓度决定。因此，以药物在设计域中的目标平均浓度与优化过程中的实际平均浓度值之差的最小值为优化目标，见式(2)和式(3)。

式中：Cobj为预设的设计域目标浓度；Cavg为优化过程中的设计域平均浓度；f(γ)为这两个数值差值的绝对值；C(γ)为设计变量的浓度。

1.5 求解模型的关键方法和参数

使用COMSOL Multiphysics软件对优化模型进行求解。选用固体各向同性材料惩罚函数(SIMP)进行优化，设计变量与材料属性之间的插值关系见式(4)。

式中：D(γi)为单元i对应的设计变量；Dmax为药物在流道区域的扩散系数；Dmin为药物在载体PCL中的扩散系数；p为惩罚系数。

采用密度过滤法对优化结果进行过滤，具体可通过耦合亥姆霍兹(Helmholtz-type)偏微分方程来实现[25]，见式(5)。

式中：Rmin为过滤半径；∇为哈密顿算子；γf为过滤后的密度值。

引入双曲正切投影函数对密度过滤后的中间值进行处理[26]。投影函数见式(6)。

式中：β为投影斜率；η为投影的阈值；γp为映射后得到的密度值。

在优化过程中，采用移动渐近线法(MMA)作为迭代算法，其收敛条件设为式(7)。当收敛容差降至10-6时完成收敛。

式中：k为迭代次数；γk是迭代次数为k时得到的设计变量值；γk-1是迭代次数为k-1时得到的设计变量值。

2 结果与讨论

对PCL/ASA药物控释系统进行拓扑优化的目的是通过改变设计域中ASA的平均浓度来实现释药量的参数化控制。为此，需首先确定ASA平均浓度的取值范围。在设计域内不设计流道的情况下，对PCL/ASA药物控释系统初始模型进行药物释放模拟，结果如图2所示。由图2可知，药物在释放初期扩散迅速；约4 d以后，整个设计域的ASA平均浓度趋于定值35.03 mol/m3，并形成了稳定的浓度梯度，该数值为设计域内不设计流道时所能达到的最大平均浓度。

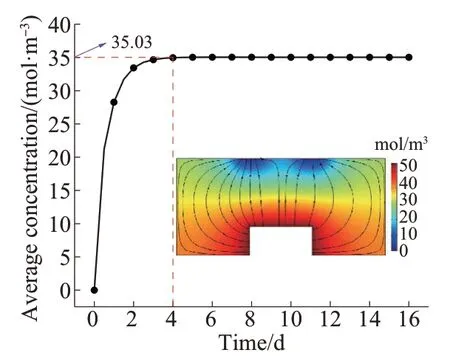
图2 优化前设计域中ASA平均浓度随时间变化的曲线Fig. 2 Curve of ASA average concentration change with time in design domain before optimization

取网格尺寸为0.08 mm、体积约束因子为0.1，设计域的目标浓度分别取41，42，43，44，45，46 mol/m3，研究不同目标浓度对流道拓扑形态的影响，结果如图3所示。由图3可知，当目标浓度小于等于43 mol/m3时，优化后的平均浓度可以达到目标值且获得了不同形态的流道结构。当目标浓度大于44 mol/m3时，平均浓度保持在43.86 mol/m3且流道结构基本保持不变。由此可知，43.86 mol/m3为当前参数下该药物控释系统所能达到的最大平均浓度值，该药物控释系统设计域的平均浓度的取值范围为35.03～43.86 mol/m3。

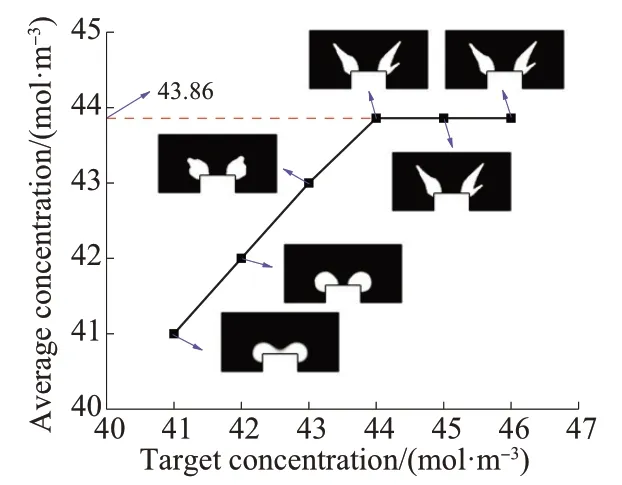
图3 设计域中目标浓度和平均浓度的关系Fig. 3 Relationship between target concentration and average concentration in design domain

2.1 拓扑优化结果的几何重构

PCL/ASA药物控释系统的药物释放是一个随时间变化的动态过程，为了研究优化结果对瞬态释药能力的影响，在相同的边界条件和初始条件下对拓扑优化模型进行几何重构。在ASA平均浓度的取值范围内，分别对平均浓度为41，42，43，43.86 mol/m3的最优拓扑优化结构进行几何重构，并分析其对PCL/ASA药物控释系统瞬态释药能力的影响。几何重构的结果如图4所示。

图4 不同ASA平均浓度的几何重构模型和拓扑优化模型Fig. 4 Geometric reconstruction model and topology optimization model of different ASA average concentrations

为了验证几何重构模型的精确性和可靠性，在初始条件不变的前提下，对几何重构模型进行瞬态数值模拟，并与拓扑优化的稳态结果进行对比分析，结果如图5所示。由图5可知，两者的平均浓度数值吻合度较高。其中，当ASA平均浓度为41 mol/m3时误差最大，这是由于在该数值下的拓扑优化结构出现了较多的灰度单元并在几何重构时被保留下来所致。

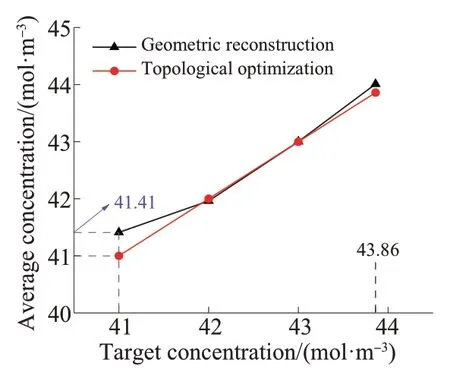
图5 拓扑优化模型与几何重构模型的平均浓度对比Fig. 5 Comparison of average concentration between topology optimization model and geometric reconstruction model

综上所述，几何重构模型能很好地还原流道的拓扑优化结构，可在最大程度上保留原拓扑优化结构的释药能力。

2.2 储库形状对释药能力的影响

为了研究储库形状对药物控释系统释药能力的影响，在储库周长相同、边界条件和初始条件不变的前提下，分别对矩形、圆形和蜂巢形3种储库形状药物控释系统的瞬态释药性能进行研究。

图6为3种不同形状储库的设计域平均浓度随时间变化的曲线。由图6可知，矩形、圆形和蜂巢三种储库形状对应的药物控释系统在达到稳定释药状态后的平均浓度分别为44.01，44.16，44.26 mol/m3，数值较为接近。由此可知，在储库周长不变的前提下，储库形状对瞬态释药能力影响较小。综合考虑载体的加工难度和脱模便利性，后续选用圆形储库的药物控释系统作为研究对象。

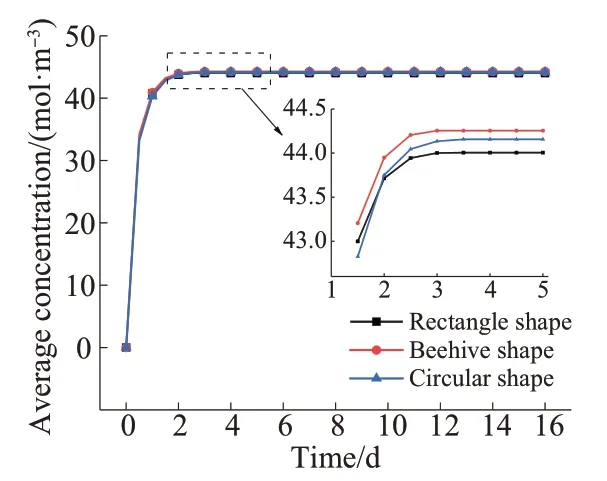
图6 几何重构模型设计域的平均浓度随时间变化的曲线Fig. 6 Curves of average concentration change with time in design domain of geometric reconstruction model

2.3 流道结构对释药能力的影响

拓扑优化方法可以将PCL/ASA药物控释系统的载体材料在设定的约束条件下达到最优分布。为了验证该方法的有效性，在储库形状不变的情况下，分别设计无流道(即未经拓扑优化)、拓扑优化流道、三角形流道和矩形流道的药物控释系统，对比分析其在瞬态下的释药能力。这4种药物控释系统均在相同条件下进行瞬态数值模拟。其中，含有流道的3种药物控释系统的流道面积均占设计域总面积的10%，如图7所示。

图7 不同流道的药物控释系统结构对比Fig. 7 Structural comparison of controlled drug delivery systems with different flow channels

图8为不同流道载体的设计域平均浓度随时间变化的曲线。由图8可知，含有流道的药物控释系统达到稳定平均浓度所需时间明显小于无流道的药物控释系统，且所能达到的最大平均浓度值明显更高。其中，拓扑优化流道的药物控释系统所能达到的平均浓度值最高，且用时最短，时间约为2 d。由此可知，经拓扑优化的药物控释系统具有更优异的释药能力。

图8 不同流道的设计域平均浓度随时间变化曲线Fig. 8 Curves of average concentration change with time in design domain with different flow channels

2.4 体外释药实验

为了验证PCL/ASA药物控释系统拓扑优化设计方法的合理性，进行体外药物释放实验。模型选用网格尺寸为0.08 mm、体积约束因子为0.1和目标浓度为43.86 mol/m3参数下的拓扑优化结构，制备方法如1.3节所述，模具和制备好的PCL/ASA药物控释系统样品如图9所示。

图9 模具型芯及制备的PCL/ASA药物控释系统Fig. 9 Mould core and prepared PCL/ASA controlled drug delivery system

图10为药物释放模拟和体外释药实验结果的对照曲线。由图10可知，具有拓扑优化流道的药物载体在14 d左右基本完成了ASA的全部释放，在释药过程中的释药速率变化较小，药物释放趋势趋于零级释放。药物释放的模拟曲线与实验结果基本一致，这验证了优化方法和模型的合理性。

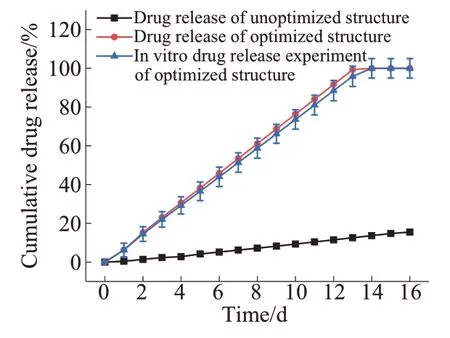
图10 药物释放模拟和体外释药实验Fig. 10 Drug release simulation and in vitro release experiment

3 结论

(1) PCL/ASA药物控释系统可以根据释药需求参数化调节设计域中ASA平均浓度，进而实现释药量的参数化调节。在网格尺寸为0.08 mm、体积约束因子为0.1的前提下，PCL/ASA药物控释系统的平均浓度可调范围为35.03～43.86 mol/m3。

(2)几何重构可以很好地保留拓扑优化后的流道结构，能充分发挥PCL/ASA药物控释系统的优势。当储库周长不变时，储库形状对药物控释系统的释药能力影响较小。此外，经拓扑优化后的药物控释系统可以缩短达到最大平均浓度所需要的时间，同时还能提高所能达到的最大平均浓度值，具有较好的释药性能。

(3)具有拓扑优化流道的药物载体的体外释药实验数据与仿真结果吻合度较好，验证了优化方法和模型的合理性。

(4)本研究在医工结合背景下，为药物控释系统的参数化设计、实现精准释药提供了新的方法和一定的理论支持。