基于改进粒子群算法的电力工程数据多目标优化方法

杨宝杰，石凯元，陈佳凯，梁富军，梁悦

（国网北京市电力公司电力建设工程咨询分公司，北京 100021）

电力建设是资金、技术和资源密集型的工程项目，在其推进过程中，易受到自然环境、管理政策与技术条件等因素的影响，从而出现工程质量下降、建设成本陡增等问题[1-4]。因此，如何实现电力工程项目的精细化及高效益管理成为电网公司亟需解决的难题之一[5-10]。当前，电力工程项目的管控决策通常在保障项目质量的前提下，以工期最短、投入最少为目标进行综合考虑，而较少考虑环境因素。随着双碳目标战略的提出，电力工程施工过程中的环境问题也成为了影响项目决策的关键因素之一。针对此，文中提出了一种电力工程数据多目标优化模型，并采用改进的粒子群算法（Improved Particle Swarm Optimization，IPSO）进行求解，进而实现电力工程项目管控的综合最优决策。

1 电力工程数据优化模型

1.1 优化目标函数

电力工程项目主要从工期、成本、质量和环境四个方面来进行综合考虑，而文中将构建涵盖以上四个目标的电力工程数据优化模型。

1）电力工程项目P在工期方面的优化目标函数为：

式中，tij为工序(i,j)花费时间；n为工序总数；T为工程P的总工期；i、j则为工程中的节点。

2）电力工程项目P的成本优化目标函数为：

式中，B和A分别为电力工程项目P延迟与提前完成工期；α、β分别为工程延迟完成的惩罚参数及提前完成的奖励参数；cij则是工序(i,j)所花费的成本，其计算方式如下：

其中，λij为控制参数；c0,ij与t0,ij为工序(i,j)的标准花费成本及时间；tij为工序(i,j) 实际花费时间。当工序(i,j)花费时间缩短或增加时，均会造成成本的增加。

3）电力工程项目的质量模型，如图1 所示。当项目所花费的时间处于正常周期时，工程质量达到最高水平；而当花费时间大于或小于正常时间时，工程质量均存在一定下降。

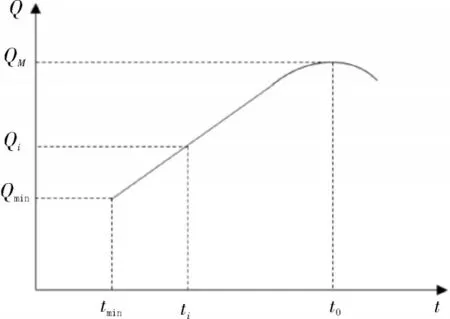
图1 电力工程项目质量模型

工序(i,j)的质量与工期关系可以描述如下：

式中，Qij为工序(i,j)质量；aij、bij分别为工序(i,j) 质量模型的一次项和常数项参数，计算方式如下：

式中，Q0,ij为工序(i,j) 需满足的最低工程质量要求；t0,ij和tij,min分别为工序(i,j) 的正常及最短工期。考虑到不同工序对电力工程项目的重要程度有所不同，则整个项目在质量方面的优化目标函数为：

式中，wij为表征工序(i,j)重要程度的权重系数。

4）为了降低环境污染，电力工程项目需加强预防和治理，而这必然导致电力工程项目投入的增加。因此，环境方面的评估指标可采用环境成本来进行描述。文中使用了线性函数，以描述环境与施工成本间的关系。由此，电力工程在环境方面的优化目标函数可表征为：

式中，Cen为环境成本；χen为环境和施工成本之间的关系系数。

1.2 约束条件

电力工程项目多目标优化需要满足以下约束条件：

1）工期约束条件。工序(i,j)除了满足施工起止时间的约束，还应满足最长工期的限制。此外，电力工程总工期也应满足相应的要求，对应的约束条件描述为：

2）质量约束。工序(i,j)质量取值范围为[0,1]，而其重要性权重系数大于0，且所有工序的重要性权重系数之和为1，则对应的约束条件描述如下：

综合上述分析，电力工程兼顾工期、成本、质量及环境的多目标优化模型为：

2 基于改进多目标粒子群算法

2.1 粒子群算法及改进

粒子群算法是一种模拟鸟类捕食模式机制的人工智能算法[11-15]，其具有全局搜索能力及较快的收敛速度，故备受青睐。

假设搜索空间维度为D，粒子种群大小为N，每个粒子均具有位置和速度两个属性，第n个粒子的位置为xn=(xn,1,xn,2,…,xn,D)；飞行速度为vn=(vn,1,vn,2,…,vn,D)；而所经过的最优位置为bestn=(bestn,1,bestn,2,…,bestn,D)；整个种群最优位置是gbest=(gbest1,gbest2,…,gbestD)，则第n个粒子属性的更新机制如下：

式中，d∈[1,D]；w为粒子飞行惯性系数；c1和c2均为学习系数，且二者分别是粒子历史最优信息及整个种群粒子最优信息的学习比例；r1与r2则为取值范围[0,1]之间的随机数。

令d=n，bestn和gbestd的更新机制如下：

在解空间搜索初期，粒子群算法中的粒子距离最优解位置较远，此时希望粒子具有较强的飞行能力，由此便可更为迅速地靠近最优解。而在算法后期，粒子位置距离最优解较近，若飞行步长过大，则易使粒子跨越最优解，且出现在最优解附近来回震荡的现象，不利于算法的收敛。针对此，文中提出以下几种改进策略：

1）惯性权重系数的改进。采用自适应的惯性权重系数，使其跟随当前迭代次数进行动态调整。当迭代次数较少时，惯性系数较大，此时可提高算法的搜索能力；而当迭代次数较大时，惯性系数较少，则提升了算法的搜索精度。惯性系数的优化表达式为：

其中，t为当前迭代次数；tmax为算法设置的最大迭代次数。

2）飞行时间的改进。在式（13）的基础上，引入“飞行时间”的概念，通过控制飞行时间参数并根据迭代次数进行自适应调整，从而增强算法的动态性能。改进之后粒子位置的更新机制如下：

式中，h为飞行时间；H0为初始飞行时间。

3）针对学习系数进行改进，使得算法初期的系数较大，而算法后期系数较小。学习系数的更新机制如下：

2.2 非支配排序算法

电力工程多目标优化模型的描述如下：

若存在解u和v满足：对于所有i∈{1,2,…,K}均有fi(u)≤fi(v)，且至少存在一个i使得fi(u)＜fi(v)，则称u支配v。当解x*不存在支配解时，x*即为多目标优化的帕累托最优解（Pareto Optimality）。利用快速非支配排序算法（Non dominated Sorting，NS）[16]实现解排序的过程如下：

1）根据当前粒子种群解的情况进行排序。每个粒子i均具有两个指标：支配粒子i的粒子数ni，以及被粒子i支配的粒子集合Si。

2）对于ni=0 的粒子，令其非支配等级为1，并将该粒子加入非支配集合F1。

3）从上次非支配集合F1中任意选取一个粒子z，并在Sz中任意选取一个粒子j，若nj-1=0，则令粒子j的非支配等级为2，且将其加入非支配集合F2中。重复上述操作，直至Fi中所有粒子均经过该处理。

4）重复上述步骤，并由此形成非支配解集F1,F2,…,Fr。

精英保留策略则从上述非支配解集F1,F2,…,Fr中按非支配等级优先的原则筛选出N个粒子。对于相同非支配等级的粒子，采用拥挤度评估其优劣。

粒子的拥挤度指标计算方式如下：

式中，fk(xi)为粒子i在第k个目标函数的取值；sgn(·)为符号函数，其表达式如下：

该次提出了非支配粒子群算法（Non-dominated Sorting Improved Particle Swarm Optimization，NSI PSO），来实现电力工程多目标优化模型的求解，算法流程如图2 所示。

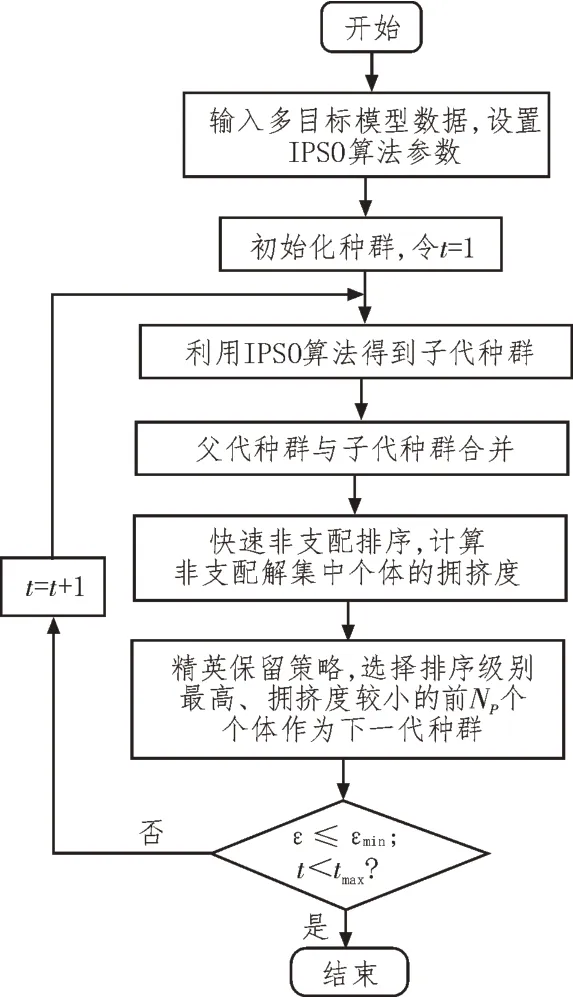
图2 NSIPSO算法求解流程

针对帕累托解集中的粒子，文中采用基于模糊满意度（Fuzzy Satisfactory Clustering）的方法实现帕累托最优解的选取，其中粒子i的模糊满意度如下：

式中，χi,k为粒子i在第k个目标函数上的模糊隶属度，其计算方式如下：

3 算例分析

为实现电力工程数据的多目标优化，文中以某省电网公司某变电站工程项目作为算例进行计算分析。所提NSIPSO 算法的参数设置，如表1 所示。

表1 NSIPSO算法参数设置

3.1 算法性能对比分析

将所提NSIPSO 与NSPSO 算法进行对比，结果如图3 所示。

图3 不同算法收敛速度对比

由图3 可知，所提算法在27 次迭代时就已经收敛，而NSPSO 算法在35 次迭代时才收敛。原因在于，文中算法通过对惯性权重、飞行时间与学习系数等的改进，提升了算法的搜索能力及收敛速度。

3.2 多目标优化结果分析

将文中所提多目标优化结果与单一目标最优的优化结果进行对比，结果如表2 所示。从表中可看出，所提多目标模型的综合模糊隶属度值为3.2，均大于单一目标最优的优化结果。由此可见，该文算法能够兼顾电力工程项目的工期、施工成本、质量及环境成本，故能为电力工程项目的管控提供技术支撑。

表2 不同样本处理参数下识别效果

4 结束语

文中开展了改进粒子群算法在电力工程数据多目标优化中的应用研究。通过数值实验结果表明，与传统NSPSO 算法相比，所提NSIPSO 算法在收敛速度与计算准确度方面均具有明显的优势，其所构建的多目标优化模型能够权衡工期、成本、质量和环境等多个优化目标，进而为电力工程管控提供更加合理的决策。但在所提算法中，仅以环境成本为优化目标进行模型构建，并未考虑SO2、CO2等温室气体的排放，而这将在后续研究中开展。