开孔方式对层装蜜桃差压预冷性能的影响
谌英敏,赵璐茜,令狐博祥,宋海燕,*
(1.山西农业大学农业工程学院,山西 太谷 030801;2.旱作农业机械关键技术与装备山西省重点实验室,山西 太谷 030801)
蜜桃味道鲜美,营养价值丰富,是典型的呼吸跃变型球类果实。其采摘季节主要集中在高温多雨的夏季,这使蜜桃采后携带大量田间热,从而增大了果实呼吸强度和乙烯释放量,加速果实成熟和变质[1]。采后预冷处理是食品冷链的第一环节,可将果温快速降低至贮藏温度以去除田间热,也可有效维持果蔬流通及贮藏品质[2-4]、降低果蔬采后质量损耗[5]以及生理活性[6],达到延长果实货架期以及保持原有新鲜度、风味的目的[7]。其中经过压差预冷处理的类球形果蔬贮藏稳定性更高[8],应用最为广泛[9-10]。
计算流体力学(computational fluid dynamics,CFD)是当下果蔬在不同预冷方式下热质传递过程数值计算领域最重要的研究手段[11-13],广泛应用于包装箱通风孔的优化设计。如Han Jiawei等[14]收集整理了市场上10 种不同开孔方式的苹果包装箱,发现最佳的包装设计取决于果蔬尺寸以及箱内果蔬与托盘的具体位置。Ambaw等[15]分析了圆形开孔(circular vent,CV)位置和衬垫材料对石榴采后预冷特性的综合影响,发现冷却速率可相差30%,而高低温区域的果蔬温度分布差异也取决于包装设计。Gong Yafang等[16]研究表明适当加大内托盘与壁面间隙宽度对缩短预冷时间、提高冷却效率、降低能耗有显著影响。Delele等[17-18]通过对比分析不同通风口设计参数(通风孔数量、位置和形状)对箱内气流和温度的影响,发现开孔率从1%提至7%,可提高183.85%的冷却速率,而当开孔率从7%提至100%时,冷却速率却只增大了62.04%,建议开孔率不超过7%。综上所得,包装箱设计是制约商业冷链中果蔬预冷性能的关键因素。同时,王晓冉等[19]通过混合正交试验发现开孔直径为20 mm时,不仅会显著提高苹果差压预冷的均匀度,也会大大降低质量损失率。Berry等[20-21]对5 层果实的预冷性能进行了多参数分析,发现多孔设计的包装箱在预冷性能和能耗方面表现最优。Dehghannya等[22]对强制风冷过程中9 种不同通风口设计(主要针对通风孔数量为1~5 个)进行了敏感性研究,观察到通风孔均匀分布在迎风面上时,农产品冷却更加均匀,并且均匀开孔的预冷性能明显强于非均匀性开孔模式[23]。然而,以上研究主要针对果蔬包装箱托盘、开孔率、开孔位置以及尺寸,对市面上常见层装蜜桃CV和矩形开孔(rectangle vent,RV)的包装预冷性能的差异性却研究较少,导致采后的层装蜜桃在不同预冷工况条件下的最佳开孔方式不明确,从而难以根据市场预冷需求对其开孔方式进行合理选择与优化设计。
因此,针对RV和CV的双层瓦楞包装箱,本研究基于CFD技术构建了单箱层装蜜桃的传热传质差压预冷数值模型,并从预冷时间、冷却效率、预冷均匀度、风机能耗这4 个方面全面分析开孔方式对蜜桃预冷性能的综合影响,为缩短果蔬预冷时间、实现快速冷藏转移以及降低预冷能耗成本提供理论指导。
1 材料与方法
1.1 材料
本次研究采用的是市场常见的两种瓦楞通风包装纸箱,开孔方式分别为RV和CV。其中CV的两个通风孔直径D=25 mm,RV的通风孔为55 mm×16 mm的长方形与两个直径为16 mm的半圆组合而成。两者的开孔率分别为3.32%和3.83%,其箱体整体设计结构以及通风孔开孔位置如图1所示。由于两种包装箱开孔率相差很小,在实验与数值计算中可忽略不计开孔大小的差异对预冷性能的影响。本次模型验证实验开展的时间为2022年8—9月,于山西省晋中市太谷地区(E112°55’,N37°43’)采摘直径约为90 mm且成熟度一致的大久保蜜桃,将其在采后2 h内进行差压预冷。
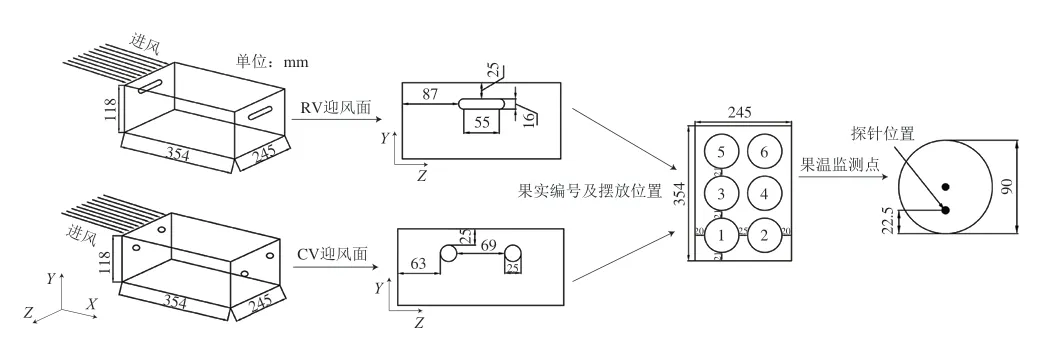
图1 两种包装箱结构设计图以及果实摆放和果温监测位置Fig.1 Schematic diagram of two packing structure designs,fruitstacking patterns and fruit temperature monitoring positions
1.2 仪器与设备
温度检测装置(8 路温度传感器)和PR -3000-FSJT-V 05 三杯风速传感器由孙义舒自制;计算机硬件配置是具有2.60 G H Z(2 个处理器)Intel®Xeon®Gold 6142F CPU和192GB RAM的64位Windows10计算机;ADT315轴流风机 天津伦登风机有限公司;TS2904PT2M风机变频器 北京同森科技有限公司;HS-05-3超声波加湿器 中国无锡洛社华盛公司;压缩机、冷凝机组、蒸发器 北京京辉源制冷设备有限公司;SSN-13E温度数字记录仪 深圳宇问加壹传感系统有限公司。
1.3 方法
1.3.1 实验操作
利用温度检测装置以及温度数字记录仪对箱内所有蜜桃的果肉半径1/2处进行果温采集(果实摆放位置如图1所示),取其平均温度作为数值模型果实初始温度。该温度采集设备的检测精度为±0.3 ℃,测量范围为-35~80 ℃,每30 s记录传输一次。实验中使用三杯风速传感器检测包装箱迎风面通风孔中心处风速情况,风速传感器的测量范围为0~30 m/s,检测精度为±0.3 m/s。果实在预冷前先启动超声波加湿器调整预冷装置内部的空气相对湿度,然后通过操作温度控制界面动态调控内部流动空气温度,风道内空气振荡幅度为±1 ℃,预冷装置结构见文献[24]。
本研究开展了1、1.5、2 m/s(通过调节风机变频器来改变送风速率)的差压预冷实验,其风机频率分别为25、30.5、36 Hz,气流振幅±0.3 m/s。实验开始前,将预冷箱中送风温度调至4 ℃。为防止在预冷过程中果实失水严重,采用超声波加湿器和湿度传感器(安装在预冷箱内)将预冷箱内相对湿度稳定在95%[25],湿度振幅为±5%。预冷环境稳定后,利用高精度数字温度记录仪和温度传感器监测箱内所有蜜桃果肉半径1/2处的果温,将其作为果实的初始温度(此次预冷实验测得所有果实的平均果温为20 ℃),并通过1.3.3.1节中公式(1)计算蜜桃的冷藏转移温度。然后马上将两种开孔方式的箱内果实分别放入预冷箱中并开始记录果实每30 s的瞬时降温数据以及迎风面气流速率,直至蜜桃降温至冷藏转移温度(当初始果温为20 ℃、气流温度为4 ℃时,果实冷藏转移温度为6 ℃)才停止记录。为了更准确反映何时达到预冷平均水平以及何时停止预冷,本研究将新鲜采摘的54 个成熟蜜桃按照图1摆放位置分9 批进行差压预冷实验(每一个送风速率重复3 次实验),并采用蜜桃果肉半径1/2处的平均温度来描述差压预冷过程的降温效果,这从整体上可以把握整个预冷过程中温度和气流场的变化规律,也能更加准确地研究其传热特性。
1.3.2 建立CFD传热传质差压预冷数值模型
1.3.2.1 物理模型与网格划分
经过市场调研及文献参考,发现蜜桃、番茄等类球型水果常用RV或CV方式的双层加固型瓦楞纸箱进行包装预冷[14-16,23-29]。因此,本研究结合实际市场需求,对RV和CV瓦楞通风纸箱的层装蜜桃进行物理建模,内包装几何规格为354 mm×245 mm×118 mm,厚度为7 mm,结构如图2所示。矩形和圆形通风孔总面积占瓦楞包装纸箱总面积的1.37%和0.62%,远低于瓦楞纸箱通风总面积要低于总包装面积3%~5%的包装结构设计要求;箱体长宽比为1.44,基本符合1.5∶1的包装工程要求[22,28-29],说明这两种瓦楞纸箱均具有较强的机械强度和托盘稳定性。

图2 差压预冷模拟示意图以及模型的网格划分Fig.2 Schematic diagram of differential pressure precooling simulation and computational grid division of numerical model
利用Meshing软件对箱内蜜桃、箱体和流体部分进行非结构化(四面体)网格划分,果实和箱体区域空间步长分别为5 mm和1 mm。瓦楞纸箱壁面与果实间保持一定空隙以实现不同计算域间的连通性[30]。两种开孔方式的包装预冷模型总网格单元数量约为1.02×106,网格质量检测得到RV和CV的Skewness值分别为84.92%和87.51%,整体偏斜度均低于90%,表明这两种模型的网格质量划分良好。
1.3.2.2 数学模型
为求解两种包装箱内部真实预冷过程的温度与流场分布情况,需要建立箱体、流体以及果肉部分计算域的数学模型。但是研究结果表明单箱蜜桃[31]和单个苹果[32]的内部呼吸热和蒸腾热等热源项的加载仅影响果实体积加权平均温度的0.1~0.3 ℃和0.033 ℃。因此,为降低数值模型计算成本,本研究对果实内部数学模型进行了简化处理,即忽略了蜜桃产生的呼吸热和蒸腾热,也忽略蜜桃间的辐射作用。同时,对物理模型的其他计算域进行了必要的假设:将空气作为不可压缩气体;蜜桃热物理参数不随温度的变化而改变,其热传导各向同性且果肉质地均匀。该模型主要包括湿冷空气、包装箱体以及蜜桃这3 个计算域,其中各计算域的计算方法详见文献[24,31],模拟计算时热物性参数如表1所示。
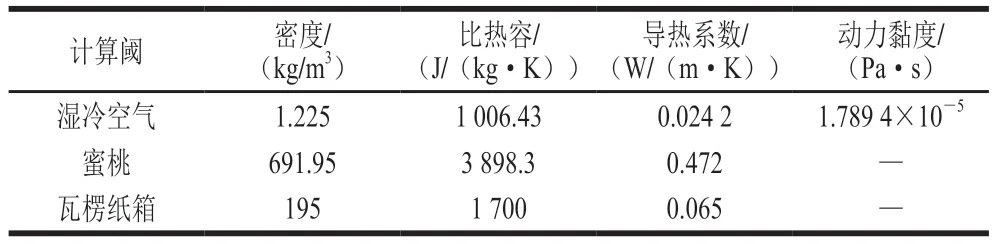
表1 湿冷空气、蜜桃、瓦楞纸箱热物性参数Table 1 Thermophysical parameters of wet cold air,peaches and corrugated boxes
1.3.2.3 初始和边界条件
初始条件:蜜桃采后均匀放置在RV和CV的包装箱内,并将箱内所有蜜桃所测量的初始温度作为模拟仿真时的初始果温,即为20 ℃。
边界条件:将箱体迎风面前500 mm处设置为压力入口边界条件,背风面1500 mm处设置为压力-外流边界条件。实验和模拟方案中,两种包装箱迎风面与背风面间的差压ΔP设置为5、15、25、35、60 Pa和100 Pa,湿冷空气温度设置为4 ℃。
壁面边界:蜜桃和箱体表面设置为零粗糙度的防滑壁条件,垂直于壁的速率分量为0,沿着计算域两侧的法向梯度也是如此。
1.3.2.4 FLUENT数值模拟方法
采用基于有限体积法的CFD商用软件Ansys 19.2进行求解计算和后处理分析。仿真时采用非稳态剪切压力传输的k-ω湍流模型并考虑空气重力影响,其中重力加速度g设置为-9.81 m/s2。将动量、能量、湍动能和扩散系数的离散格式均设置为二阶迎风格式,并利用基于压力的分离求解器进行求解,即采用压力速度耦合算法。空气流体计算域的控制方程为质量守恒方程、动量守恒方程以及能量守恒方程。仿真时时间步长设置为30 s,其连续性、动量和湍流的收敛准则设置为10-4,能量方程的收敛准则设置为10-6。
1.3.3 评估参数
1.3.3.1 无量纲温度
冷却时间、速率、均匀度和风机能耗是差压预冷过程中评价果实预冷性能的重要指标。本研究将以这4 个参数作为评估这两种通风口包装箱预冷性能优劣的标准。为准确反映果实预冷过程,通常使用无量纲温度(Y)进行分析[16,32-33],其中Y=1/2和Y=1/8被用来衡量果实是否达到预冷平均水平及冷藏转移温度,该时间点被称为1/2(half cooling time,HCT)和7/8预冷时间(seven-eight cooling time,SECT),其计算如式(1)、(2)所示:
式中:Ti,vol为某一时刻第i号果实体积加权平均温度/℃;Ta为冷空气温度/℃,实验时预冷装置内的冷空气温度设置为4 ℃;T0为果实初始温度/℃;Vi为果实内部第i个网格体积/m3;Ti为果实内部第i个网格的温度/℃;Vt为单个果实总体积/m3。
1.3.3.2 温度异质性指数(heterogeneity index,HI)
HI可用来反映果实预冷均匀性,是判断果实在不同预冷工况条件下其预冷品质良好的重要指标[16,27,33-35]。HI越大,表示箱体内部果实温度离散程度越大,其冷却均匀性越差,反之则预冷均匀性越好。因为果实贮藏温度对其品质有着决定性影响作用,当果蔬预冷时进出风口处位置的果实如果依然保持较大温差,会造成果实间二次热传递效应,形成热污染现象,从而会在该区域形成“腐烂源”[34],并逐渐向四周传递,这无疑是增大了果实腐烂率。HI计算如式(3)所示:
式中:HIp,t为t时刻第p个果实的HI;为t时刻所有果实的平均温度/℃;Tp,t为t时刻第p个果实的温度/℃;n为所测果实总个数。
1.3.3.3 风机能耗
差压预冷过程中降低制冷系统的能耗可减少预冷成本,也可提高果实冷链物流行业中的能源利用率,实现节能减排与低碳生活。制冷系统中风机能耗是果实差压预冷过程中消耗的主要能量,并且果实在7/8预冷时间后将冷藏转移至贮藏设备中以消耗剩下的微量田间热。因此,7/8预冷时间内的风机能耗是评估果蔬是否节能预冷的关键因素,其计算如式(4)所示[35]:
式中:Ew为风机能耗/J;t为预冷时间/s;Pw为风机功率/W,可由压降ΔP/Pa和体积流量G/(m3/s)计算得出,其函数关系为:Pw=ΔP×G。
1.3.3.4 误差分析
为了验证模型准确性,通常使用均方根误差(root mean square error,RMSE)和平均绝对百分比误差(mean absolute percentage error,MAPE)对预测果温Si/℃和实验测得果温Ei/℃进行比较分析。其计算分别如式(5)、(6)所示:
1.4 数据处理与分析
所有数据用Excel 2010和MATLAB R2022b软件进行统计与处理,采用Origin 2018软件绘制折线图,并进一步优化图形,采用CFD-Post 19.2和Visio软件处理模拟计算后温度和速度分布云图数据。
2 结果与分析
2.1 实验与模型验证
图3为15、35 Pa和60 Pa(即送风速率分别为1、1.5 m/s和2 m/s)的模拟与实验验证曲线,图中显示,模拟与实验中的蜜桃降温趋势一致,均随预冷时间的延长而逐渐下降。其中,两者间的RMSE和MAPE最大值分别为0.799 ℃和6.6%,最小值分别为0.334 ℃和3.5%(表2)。由此发现,该模型仿真数据与实验间的RMSE均小于1 ℃,MAPE也小于10%,这远小于Gong Yafang[16]和Han Jiawei[14]等提出的单箱苹果强制风冷数值模型的预测误差,即最大的RMSE分别为1.778 ℃和0.82 ℃,其MAPE分别为7.76%和18.69%。这些数据充分表明模拟与实验值具有较高的一致性。存在的误差主要来源于实验仪器自身的误差以及送风速度和送风温度的波动,但不影响预测数据的可靠性。
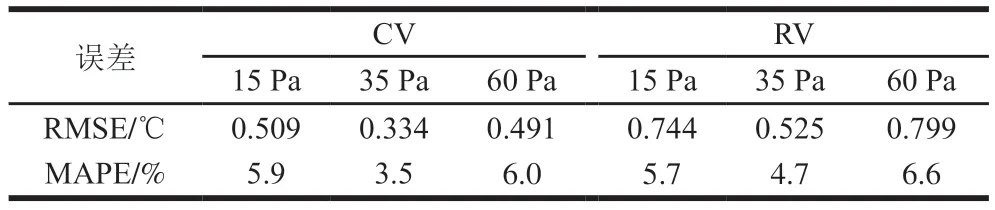
表2 不同差压下实验与模拟数值的误差分析Table 2 Error analysis of experimental and simulated values for different differential pressures

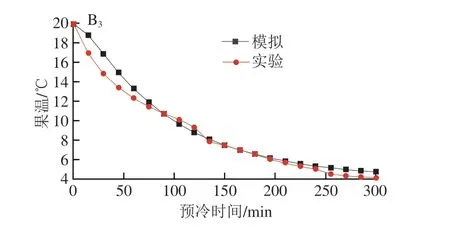
图3 不同差压下的数值模型验证Fig.3 Numerical model validations at different differential pressures
2.2 开孔方式对预冷速率的影响
观察表3中不同差压条件下两种开孔方式的HCT和SECT值,发现层装蜜桃的冷却系数C、滞后因子J在随着ΔP的增大而逐渐增大。不同ΔP间的ΔHCT和ΔSECT值呈逐渐缩小的趋势,其中RV的最大ΔHCT和ΔSECT值分别为49 min和150 min,CV的最大ΔHCT和ΔSECT值分别为33 min和88 min。并且两种开孔方式的ΔHCT和ΔSECT最大值均集中在5~15 Pa间,这说明蜜桃预冷差压条件在低于15 Pa时对预冷时间的影响最为显著。此外,当ΔP为5、15、25、35、60 Pa和100 Pa时,CV的HCT值较RV分别缩短了33.78%、34.34%、44.79%、34.25%、34.43%、34.62%,其SECT值也分别缩短了36.30%、33.78%、38.87%、34.53%、34.04%、30.52%,由此发现CV较RV的预冷时间整体缩短了30%~40%。
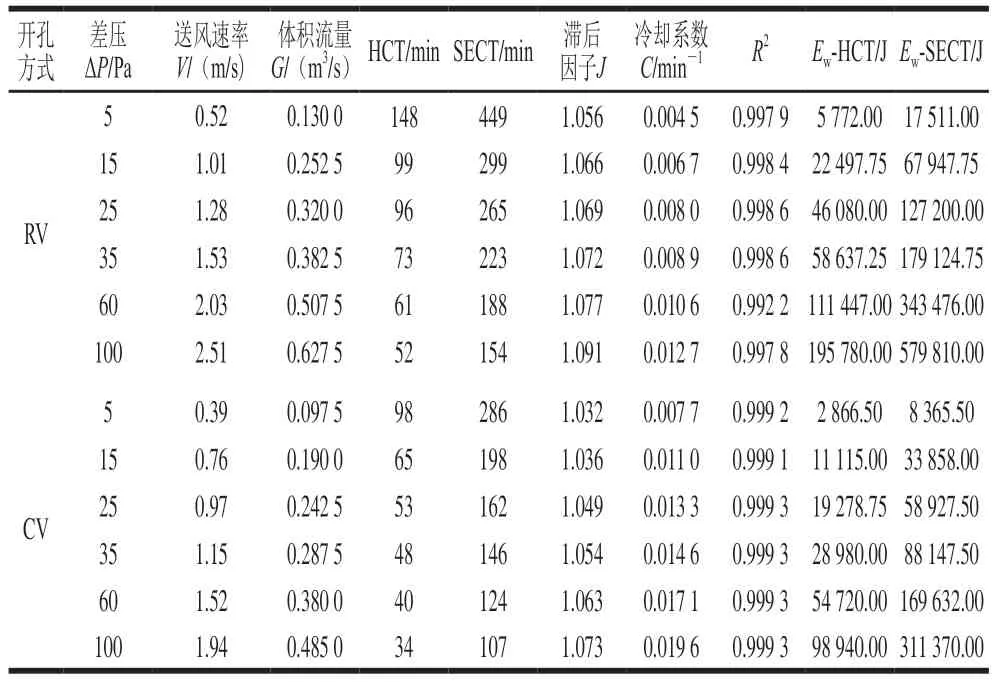
表3 不同差压ΔP条件下的送风速率V、体积流量G、预冷时间(HCT和SECT)和冷却速率Table 3 Air-inflow velocities (V),volumetric flow rates (G),half and seven-eighths cooling time (HCT and SECT) and cooling coefficients for different differential pressures (ΔP)
将两种开孔方式的HCT、SECT值分别与ΔP进行拟合时,得知该数学模型均为幂函数,即t=a×ΔPb,其中a和b为常数,且决定系数R2均高于97.76%。并且ΔP与风速V、体积流量G间的函数关系符合方程:aΔP2+bΔP+c,其中a、b和c均为常数且R2高达99.49%和99.36%(表4)。由此可通过上述ΔP与送风速率、体积流量间的线性递增函数,进一步推导出预冷时间HCT、SECT与风速V、体积流量G间的直接函数关系。此外,Defraeye等[33]也总结归纳出了类球形果蔬预冷过程中无量纲温度Y与预冷时间t间的函数模型,即Y=Je-Ct,将其转换成公式(7):

表4 预冷性能与不同差压ΔP间的函数关系Table 4 Functional relationships between precooling performance and different differential pressures (ΔP)
利用不同预冷工况条件下果实的降温数据,建立冷却系数C、滞后因子J的数学模型,即为式(8)~(11):
将式(8)~(11)代入式(7)中,可得预冷时间t与差压ΔP间的函数关系,分别为式(12)、(13):
因此,综合上述所建数学模型(12)、(13)可得到不同开孔方式下蜜桃的HCT和SECT预测值,与实测值相比,RV的RMSEHCT=5.77 min和RMSESECT=20.60 min,其MAPEHCT=5.94%和MAPESECT=8.36%,CV的RMSEHCT=5.24 min和RMSESECT=18.73 min,其MAPEHCT=4.45%和MAPESECT=9.42%。而利用本研究所提出的预冷时间HCT和SECT的数学模型t=a×ΔPb进行预测时,与实测值相比,RV的RMSEHCT=4.81 min和RMSESECT=5.12 min,其MAPEHCT=3.78%和MAPESECT=1.56%,CV的RMSEHCT=0.79 min和RMSESECT=2.24 min,其MAPEHCT=1.40%和MAPESECT=1.34%。对比这两种数学模型的预测误差值,发现数学模型t=a×ΔPb在预测HCT时,其RMSE和MAPE值分别低于5 min和5%,而在预测SECT时,其RMSE和MAPE值则约低于5 min和2%,这远远低于数学模型(12)、(13)所预测的数据值误差。这些数据表明,虽然两种数学模型的预测误差均小于10%,皆可用于预测HCT和SECT,但是数学模型t=a×ΔPb的预测精度更高,更便于快速掌握果实冷藏转移时间以延长果实货架期。
2.3 开孔方式对预冷均匀度的影响
图4表达了不同差压条件下CV和RV的HI以及两者间HI差值(ΔHI)分别随预冷时间延长的瞬态变化。仔细观察图的变化曲线,发现两种开孔方式的HI值基本随差压ΔP的增大逐渐减小,这与韩佳伟等[27]提出的温度变异系数随送风速率的增大而降低的关系一致,当差压ΔP为5、15、25、35、60 Pa和100 Pa时,RV的HI峰值分别为14.08%、12.27%、11.30%、11.23%、10.82%和10.71%,CV的HI峰值分别为18.85%、18.71%、17.48%、17.63%、16.66%和14.99%。同时,在Q点(即两种开孔方式的HI曲线交点)前ΔHI一直大于零,呈先增大后减小的趋势。在此期间,两种开孔方式的预冷均匀性差异ΔHI在CV进行冷藏转移前早已达到了峰值,在5、15、25、35、60 Pa和100 Pa差压条件下的峰值分别为5.69%、7.42%、8.23%、7.67%、7.02%和5.89%。这些数据充分说明CV在进行冷藏转移前,其预冷均匀度明显低于RV。造成这种差异的原因是RV的温度变化梯度较CV更小,数据显示(图5)RV和CV的箱内果实在预冷90 min时,整体的瞬时温度变化范围分别为2.91~5.82 ℃和4.36~10.18 ℃,而在预冷120 min时,其范围缩小至2.91~4.36 ℃和2.91~7.28 ℃。这表明RV进出风口处的果温差异明显小于CV,导致RV进出风口间果实的二次热传递效应远远低于CV,从而致使RV更有利于果实均匀预冷。造成这种现象的原因是(结合图6)冷空气流经RV时,大部分气流集中于中间风道,出现“短路”现象。且随着风速的增大,聚集在出风口处气流越来越多,向其两侧蜜桃扩散的气流也逐渐增多,导致出风口处区域的蜜桃冷却速率更快。然而气流流经CV时,大部分气流直接撞击进风口处果实,导致气流形式从层流转为湍流,并集中于进风口,造成进风口处果实降温速率远远高于出风口,从而引发箱内果实间更高的二次热传递效应,使其热污染显著。
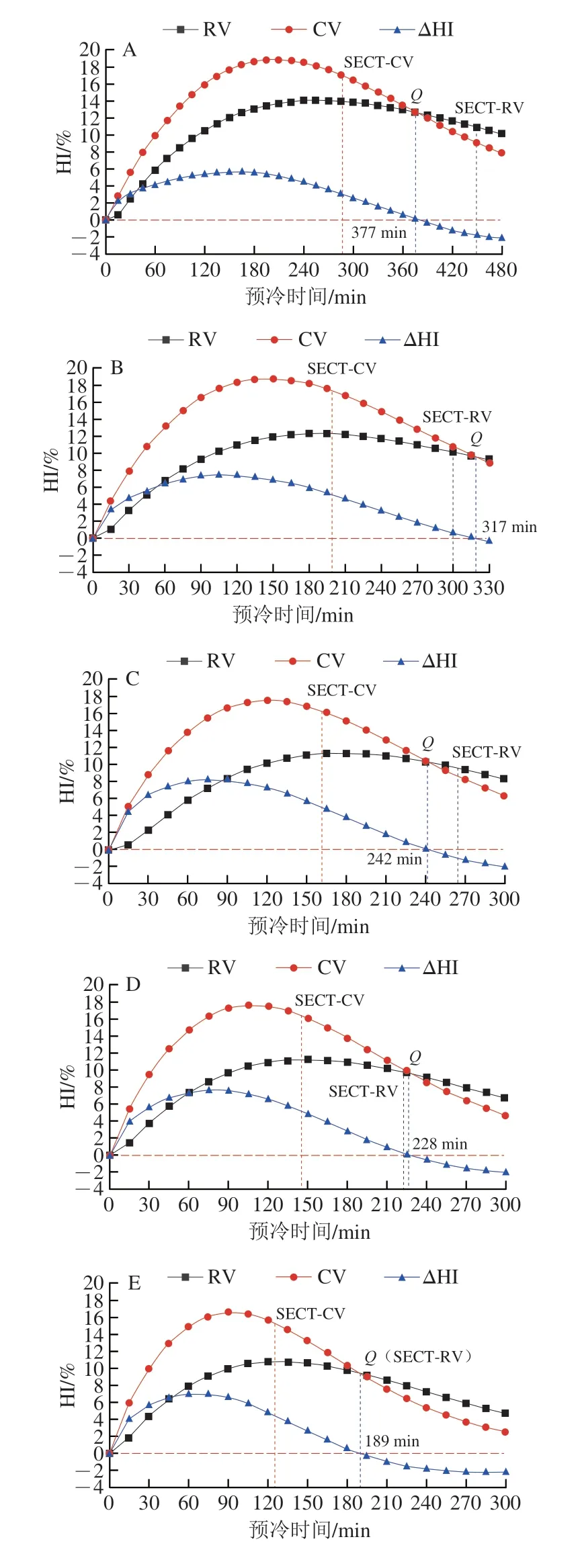
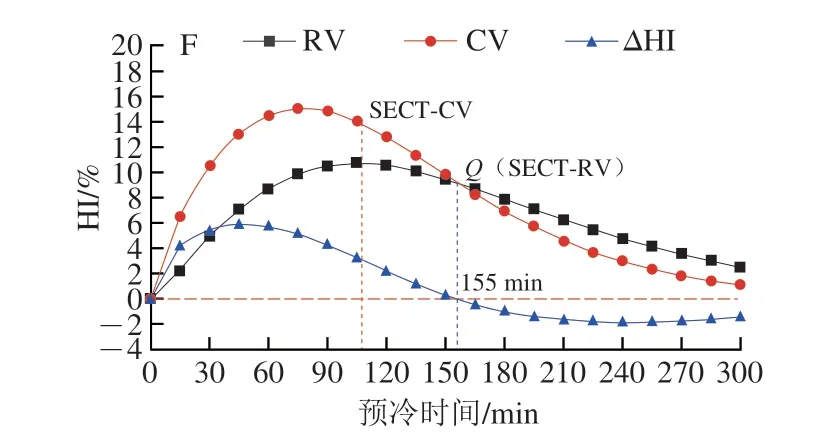
图4 温度变异系数变化曲线Fig.4 Change curves of temperature variation coefficients

图5 不同开孔方式在不同差压情况下各果实的瞬态温度分布云图Fig.5 Instantaneous static temperature contours of each peach in different vent modes at different differential pressure conditions

图6 在60 min的速率分布云图Fig.6 Instantaneous contours of different velocities at 60 min
在Q点后,其ΔHI一直小于零,出现了HIRV>HICV的情况。但是CV的SECT在Q点前,并且在ΔP高于35 Pa后,RV的SECT值基本与Q点重合。这表明在Q点前两种包装设计的预冷蜜桃大多进行了冷藏转移。因此,本研究不需要进一步探讨Q点之后预冷均匀性的“拐点”变化。由此,综合上述分析,可知蜜桃在其整个SECT内CV的预冷均匀性明显差于RV。
2.4 开孔方式对风机能耗的影响
利用两种不同开孔方式的包装箱进行预冷时,所消耗的风机能耗以及能耗与ΔP间的函数关系如表3、4所示。由表4可知,ΔP与风机能耗Ew呈幂函数关系(即Ew=a×ΔPb),这与Han Jiawei等[36]描述的能耗与送风速率呈幂律关系的结论一致,这是由于HCT、SECT与ΔP呈幂函数关系。此外,不同差压条件下,两种开孔方式在HCT内的风机能耗(Ew-HCT)约为SECT内(Ew-SECT)的1/3,约2/3的能耗用于HCT之后的降温过程。造成这种情况的原因是HCT到SECT的这段时间约占总预冷时间的67%,并且CV的Ew-HCT和Ew-SECT较RV少了约50%。这表明虽然RV的预冷均匀性更好,但由于其SECT较CV约长了55%(表3),导致使用RV预冷时会消耗更多的风机能量。
2.5 瓦楞纸箱开孔结构改进措施
通过分析层装蜜桃在不同开口方式下的预冷时间、预冷均匀度和风机能耗,发现相较于RV,CV的预冷时间能缩短30%~40%,其能耗也能降低50%,但是这些性能的提高是建立在牺牲预冷品质的基础上实现的。基于此,为提高圆形通风孔包装的预冷均匀性,本文将对其结构进行优化设计。调整圆形通风孔的开孔直径,将其从25 mm分别增大到30、35 mm和40 mm,并利用计算流体热力学技术获取ΔP=60 Pa时整个预冷过程的HI值,如图7所示。这是因为蜜桃适合在1.5~2.5 m/s[35]的风速下预冷,而当ΔP=60 Pa时,所监测到的通风孔中心位置风速分别约为1.9、2.2 m/s和2.5 m/s,均在适宜的送风速率范围之内。仔细观察图7发现,采用不同圆形通风孔直径的瓦楞纸箱预冷时,其HI值在随着开孔直径的增大而逐渐减小,这意味着果实的预冷均匀性在不断提高,而当开孔直径大于35 mm后,果实各个时刻的HI值开始低于RV。同时,结合图8可知,CV开孔直径在25~40 mm的90 min瞬时温度变化梯度分别约为4.37、2.91、1.46 ℃和0.87 ℃,与RV相比(约为2.91 ℃),开孔直径在大于35 mm后的温度变化梯度会更小,更能让果实均匀地降温。
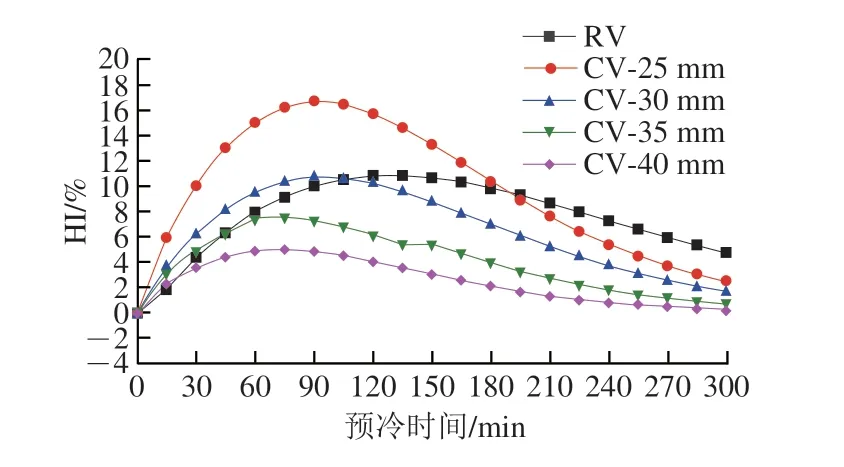
图7 不同开孔方式下温度异质性变化曲线(ΔP=60 Pa)Fig.7 Change curves of temperature heterogeneity index in different vent modes (ΔP=60 Pa)

图8 不同CV直径下各果实的瞬态温度分布云图(ΔP=60 Pa)Fig.8 Instantaneous static temperature contours of each peach with different diameters of CV (ΔP=60 Pa)
3 结论
本研究以层装蜜桃为研究对象,对市场常见RV和CV瓦楞纸箱(含果实)进行差压预冷实验和CFD仿真分析,从预冷时间、预冷均匀性、风机能耗等方面探讨了两种开孔方式对差压预冷性能的综合影响。具体结果如下:
1)建立了CV和RV的传热传质差压预冷数值模型并用实验验证了该模型的预测精准性,其最大RMSE和MAPE分别为0.799 ℃和6.6%,整体预测误差小于10%,果温预测误差小于1 ℃。
2)CV的预冷均匀性明显差于RV,但其预冷时间较RV却缩短了30%~40%,造成的风机能耗也减少了50%。由此发现,使用CV瓦楞纸箱能节约更多能耗成本,实现果实快速冷藏转移,而使用RV瓦楞纸箱时更能保障果实的预冷品质。然而,当CV开孔直径大于35 mm后,既能实现果实快速高效节能预冷,也能保障果实更均匀地冷却。
3)两种开孔方式的进风口风速V、体积流量G与差压ΔP为线性递增函数,并且其预冷时间HCT和SECT、风机能耗与差压ΔP均呈幂函数关系(t=a×ΔPb)。该数学模型的构建为快速精准掌握不同预冷工况条件下的预冷性能、合理选择最佳的开孔方式提供了理论参考依据。

