基于T2VOC对比分析LNAPL多种因素运移的数值模拟

侯岳岚，夏 源，程亚平,3，周正涛

（1.桂林水文中心，广西 桂林 541199；2.桂林理工大学，广西 桂林 541006；3.岩溶地区水污染控制与用水安全保障协同创新中心，广西 桂林 541006)

0 引言

不与包气带及潜水面以下的水发生混合的液体通常称为非水相液体（nonaqueous phase liquids，NAPLs），其中密度比水小的叫做轻非水相液体（Light Non Aqueous Phase Liquid，LNAPL）。LNAPL属于挥发性有机污染物（VOCs），不与水混合且很难自然降解，在地下水系统中能停留数年至数十年之久，对地下水环境系统造成严重破坏。其泄漏后，属于“NAPL-液-气”多相流的问题，其中：LNAPL自由态和残余固态属于NAPL 相，溶于水后溶解态属于液相，挥发在空气中属于气相[1-2]。目前大多数学者通过“NAPL-液-气”三相流体系描述LNAPL在地下环境迁移形式[3]。

LNAPL 污染物迁移过程复杂，受多种因素影响。施小清、李晔等[4-5]运用T2VOC程序、NAPL sim⁃ulator 模型与土壤相对介电常数等方法研究出NAPLs 泄漏速率对其在非饱和带中的运移范围影响。杨明星[6]为研究水位波动带对不同类型的石油污染物产生成分和分布的变化，利用TMVOC 程序数值模拟和室内试验进行验证，不同污染物组分在非均质土壤中渗入滞留在界面附近，污染物自由态的浓度也受水位波动下水流冲刷作用逐渐升高。潘明浩等[7]为揭示透镜体与地下水波动相互作用下非水相液体的迁移过程，利用TOUGH2 程序中TMOVC 模块建立LNAPLs 在包气带运移的多相流数值模型，结果表明：地下水位恒定时，粗砂透镜体有助于LNAPL 垂向迁移。王颖等[8]基于TMVOC 模型模拟分析LNAPL 受水位波动所引起的污染范围与质量变化。

就目前的研究可知，多种因素影响着LNAPL的溶解速率，但对其受因素的变化及影响的敏感度研究还是空白。本文采用TOUGH2 软件对LNAPL 进行数值模拟，选取地下水流速率、LNAPL 的泄漏强度、地下水位波动等影响因素，对比分析上述几种因素对LNAPL 溶解速率的变化及其敏感度，为LNAPL的溶解迁移模拟提供源强依据。

1 计算方法

1.1 控制方程

由于多相流模型具有高度非线性的特点，本文采用由美国劳伦斯—伯克利国家实验室（LBNL）开发的TOUGH2 软件中T2VOC 模块求解，T2VOC 模块求解采用数值法，适用于多相流模型[9]。在TOUGH（非饱和地下水流及热流传输）数值模拟程序中，可以分别模拟一维，二维和三维孔隙或裂隙介质中多相流、多组分及非等温的水流及热量运移。T2VOC 程序运用积分有限差分法（IFDM）进行空间离散，将水、气及NAPL视为三相且假设均符合Darcy定律，三相运移根据压力和重力确定[10]。在包含三个质量分量的非等温系统中，需要三个质量平衡方程和一个能量平衡方程来完整描述系统，对于表面积为n的任意流动区域Vn，以积分的形式写出：

式中：Mk为每单位多孔介质体积中组分K（K=w，a，c）的质量；Fk为组分K进入体积Vn的质量通量；n为内法线方向的单位向量；qk为单位体积内组分K的源汇项。

1.2 概念模型

考虑污染物苯泄漏速率、地下水位波动、地下水流速3 种影响因素，采用单因素敏感度分析法对3 种影响因素影响下LNAPL 的溶解速率做敏感度分析，得出各因素对LNAPL溶出质量的敏感度。建立以下情景：

（1）地下水流速。建立3种情景地下水流速率模型，分别为情景A-1（低流速）、情景A-2（中流速）、情景A-3（高流速）。

（2）泄漏强度。建立3 种情景泄漏强度模型，分别为情景B-1（弱泄漏）、情景B-2（中泄漏）、情景B-3（强泄漏）。

（3）地下水位波动。建立3 种水位波动模型，分别为情景C-1（无波动）、情景C-2（低波动）、情景C-3（高波动）。

由于模拟的情景多，计算量大，而敏感度分析的目的是为了评价影响因素对溶出质量的影响强弱，对模拟的精度要求相对不高，因此对模型缩小计算尺度，并减少剖分的网格数量，以减少计算量。假设模拟区域为均质中砂，尺寸为10 m×3 m×3 m的矩形砂槽（见图1），X、Y、Z方向均匀剖分为25×15×15共5625个单元格，其中单位单元格尺寸为0.4 m×0.2 m×0.2 m，顶部边界为封闭边界，左右边界为定水头边界，下部边界为隔水边界。选取苯（benzene）为本次研究的LNAPL污染物。

为了便于对比分析，不考虑热物理相关参数，苯的理化性质参数选取TOUGH2 程序提供的VOC数据集里面的部分参数（见表1）。

表1 模型中主要参数

初始模型污染源尺寸为0.4 m×0.2 m 的矩形设于模型区域顶部中心轴下游3 m 处，污染物苯以5.55×10-4kg/s速度持续泄漏6 h，改变初始条件考虑地下水流速、渗透速率、地下水位波动3 种因素，比较他们对LNAPL的溶解速率的影响。

2 结果与分析

2.1 地下水流速的影响

首先考虑地下水水流速率对LNAPL 运移的影响，利用改变左右边界的水头差调整水力梯度，采用达西定律计算出地下水流速。情景A-1水流速率为0.38 m/d；情景A-2 水流速率为0.77 m/d；情景A-3水流速率为1.54 m/d。3种情景下压强分布见图2。

图2 3种情景下压强分布

模型运行6 h时，污染源苯停止泄漏，此时液相饱和度分布见图3。由图3 可知，3 种情景下XZ剖面液相饱和度的面积分别为5.252、5.566、6.0 615 m2。其中高饱和液相饱和度面积分别为0.1 708、0.2 149、0.2 520 m2。对比情景A-1的液相饱和度面积，情景A-2 中2 倍水流速率增加5.98%，情景A-3中4倍水流速率增加15.41%，相对于情景A-2约2.5倍。对比情景A-1中高饱和液相饱和度面积，情景A-2增加25.82%，情景A-3增加47.54%，相对于情景A-2约2倍左右。结合质量溶出速率与NAPL-水界面面积之间的关系，可知呈倍数的增加地下水水流速率促使LNAPL 中NAPL 相溶解到水中数量呈倍数的增加，其质心面积变异程度受地下水流速率影响较大。

图3 3种情景下苯泄漏6 h液相饱和度分布

持续监测受此影响因素下LNAPL 溶解速率变化（见图4）。由图4 可知，模型运行前13 h 溶解速率数值波动较大，情景A-3 基本处于3 种情景中的较大值，13 h后LNAPL的NAPL相达到稳定状态，溶解速率趋于稳定，可以看出：地下水流速率与溶解速率呈现正相关趋势。

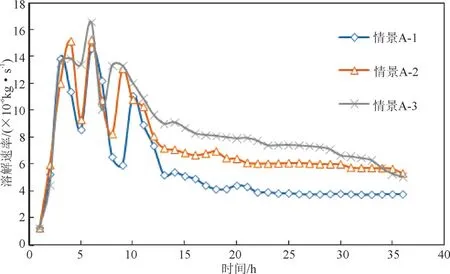
图4 3种情景下各时刻溶解速率变化

2.2 泄漏强度的影响

泄漏强度对LNAPL 的污染范围和浓度分布有明显的影响，故考虑其对泄漏在地下水环境中LNAPL 的溶解速率的变化，保持泄漏总量不变，改变泄漏速率设置3 种情景。情景B-1 模型与情景A-1模型一致，苯泄漏速率为5.55×10-4kg/s，持续泄漏6 h；情景B-2 中苯泄漏速率增加5 倍，为2.775×10-3kg/s，持续泄漏72 min；情景3 中苯泄漏速率增加10 倍，为5.55×10-3kg/s，持续泄漏36 min。模型运行6 h 后，3 种情景下污染物苯都已泄漏完成，因LNAPL 的液相主要由NAPL 相溶解，故对NAPL 相苯进行监测，结果见图5。由图5 可知，3 种情景中高NAPL相饱和度分别可达0.342，0.241，0.236。

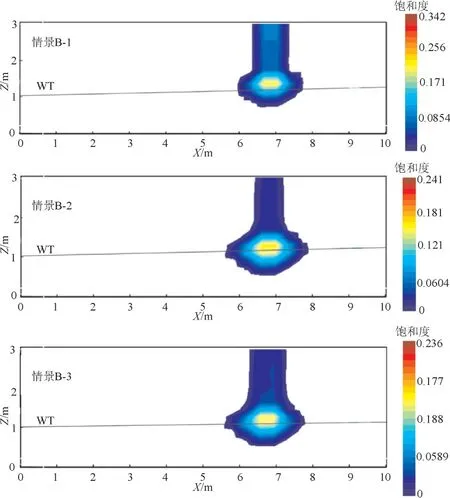
图5 3种情景下模型运行6 h后NAPL相饱和度分布

3 种情景下各时刻溶解速率图见图6。由图6可知，前15 h曲线波动剧烈，情景1中溶解速率曲线值忽高忽低，这是由于其泄漏速率低，持续泄漏量小，受地下水流速率影响造成一定波动；情景B-2中前2 h由于随着污染物的持续泄漏导致溶解速率曲线值有一个变大的波动值，待泄漏停止，溶解速率降低，后随着模型运行溶解速率趋向稳定。对20 h后曲线值进行放大，可以看出模型稳定后，泄漏速率越大，溶解速率越低，LNAPL中NAPL相对越少溶解于水中，造成更多残留相滞留于地下水环境中。结合图5 可知，泄漏速率与NAPL 相饱和度呈现反相关，NAPL相饱和度与溶解速率呈现正相关。

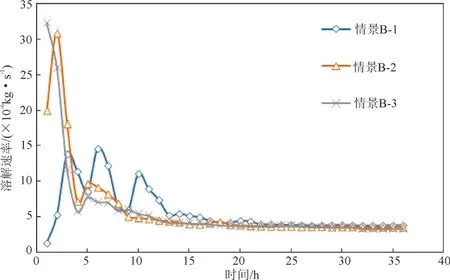
图6 3种情景下各时刻溶解速率图

2.3 地下水位波动的影响

LNAPL 泄漏在地下水环境中主要分布在毛细水带与地下水位波动带附近，潜水面波动能够对其相态分配转化产生重大影响。鉴于此，模型中通过上边界注水模拟降雨条件，建立3 种情景（见表2）对地下水位波动因素引起的LNAPL 溶解速率的变化进行对比分析。情景C-1 与情景A-1、情景B-1模型初始条件一致；情景C-2 中考虑日降雨量50 mm（大雨），降雨速率为4.6 296×10-5kg/s，待情景C-1中污染物苯泄漏完成，通过降雨1d使得LNAPL在水位波动状态下自由扩散以致达到稳定状态；情景C-3模拟情景与情景C-2相似，降雨1 d考虑日降雨量为100 mm（大暴雨），降雨速率为9.2 592×10-5kg/s。3种情景下各时刻溶解速率图见图7。由图7可知，3种情景中情景C-3降雨量最大，其处于水位上升状态时，LNAPL 中NAPL 相的溶解速率处于最高值，而当其处于水位下降直至稳定过程中，溶解速率处于3种情景中的最小值。水位上升引起的溶解速率增加有两点原因：第一点是由于降雨引起的淋滤作用下毛细水带中污染物LNAPL浸涂区里NAPL相被冲刷出来，导致LNAPL 的NAPL 相饱和度增加，故增大苯自由相的溶解速率；第二点是由于水位上升为自由态LNAPL提供浮力，驱替土壤孔隙中自由态漂浮出来，也对LNAPL 的NAPL 相饱和度增加起关键作用。情景C-3 中水位下降携带更多的NAPL相苯使得溶解速率有一定的增幅，待水位稳定后，由于先前的一系列波动，NAPL相饱和度已经处于3种情景中的最低值，故溶解速率会处于最低值。

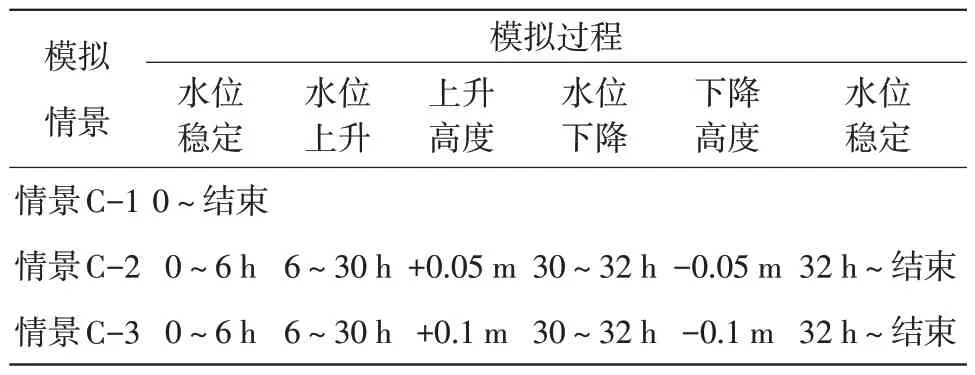
表2 不同降雨条件下模拟过程设计

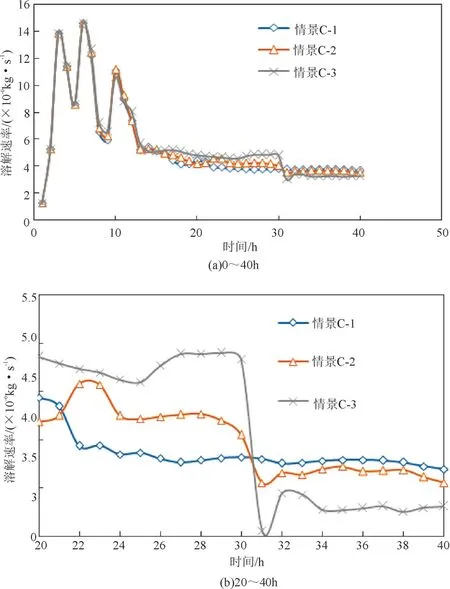
图7 3种情景下各时刻溶解速率图

2.4 敏感度分析

综上，地下水流速率、泄漏速率、地下水位波动均对LNAPL 的溶解速率产生一定的影响。单因素敏感性分析可用敏感度系数表示项目评价指标对不确定因素的敏感程度[11-13]，其表达式为：

式中：ΔF为不确定因素F的变化率；ΔA为不确定因素F发生ΔF变化率时，评价指标A的相应变化率；E为评价指标A对于不确定因素F的敏感度系数。

本文E为无量纲数，如计算出正负值，则做绝对值处理（方便观测比较）。对地下水流速率因素，敏感度系数E表示NAPL相质量溶出速率变化倍数比地下水流速增大倍数，其中敏感度系数E1、E2中地下水流速增大倍数分别为2 倍、4 倍，对E1、E2进行回归分析，结果见图8 和表3。由图8 和表3 可知，拟合预测模型1、模型2的R2分别为0.57、0.85，均拟合效果较好。从拟合结果来看，地下水流速率每增大1 倍，其敏感度系数E1、E2 变化在0.1～0.3 之间；当地下水流速率增大4 倍时，拟合出敏感度系数在区间变化中相对较小。

表3 地下水流速、泄漏强度、地下水位波动的敏感度系数拟合预测模型

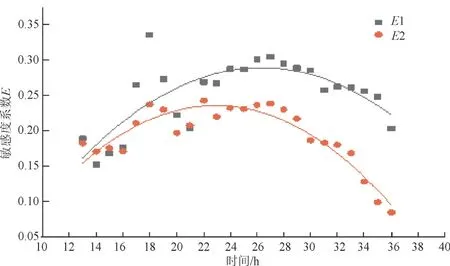
图8 地下水流速率敏感度系数分布

对LNAPL 泄漏强度因素，敏感度系数E表示NAPL相质量溶出速率倍数比其LNAPL泄漏强度增大倍数，其中敏感度系数E3、E4中LNAPL泄漏强度增大倍数分别为5 倍、10 倍。对E3、E4 所得的敏感度数据结果进行观测，发现在22～44 h 之间E值波动较为剧烈，44 h 后，E3、E4 值均趋向于0.0 085，故对在22～44 h之间的E值采用3项式线性拟合，结果见图9和表3。由图9和表3可知，回归模型3、模型4 的预测值与敏感度实际值之间的R2分别为0.88、0.93，拟合效果较好。回归模型3 敏感度系数在0.004～0.012之间，模型4敏感度系数在0.002～0.011之间，综合来看，E3＞E4，说明采用10倍LNAPL泄漏强度计算敏感度比用其5倍泄漏强度所得的敏感度系数低，模型运行后期，泄漏强度对LNAPL 的敏感度系数较低，趋向于0.0 085。

图9 LNAPL渗透速率敏感度系数分布

对于地下水位波动因素的敏感度分析，由图7可知，降雨造成的水位波动下使得LNAPL的质量溶出速率受水位上升下降有不同的变化，故其敏感度按水位上升和水位下降进行分析（见图10）。假设水位上升0.05 m为水位上升波动1倍，水位上升0.1 m为波动2倍，图10（a）中E表示NAPL相质量溶出速率倍数比水位上升下降波动倍数，其中敏感度系数E5、E6 中水位上升波动倍数分别为1 倍、2 倍，敏感度系数E7、E8中水位下降波动倍数分别为1倍、2倍。观察E5、E6敏感度系数分布，选用一元线性模型进行拟合，结果显示R2分别为0.62、0.71，拟合结果较好，其E值为0～0.15，E6 斜率比E5 较大，说明水位上升较高时计算所得E值较大。图10（b）中E7、E8选用一元线性模型进行拟合，结果显示R2分别为0.91、0.93，拟合效果良好，其E值为0.02～0.08，可以看出水位下降对NAPL相质量溶出速率影响最高可达0.08，后随时间变化逐渐降低。

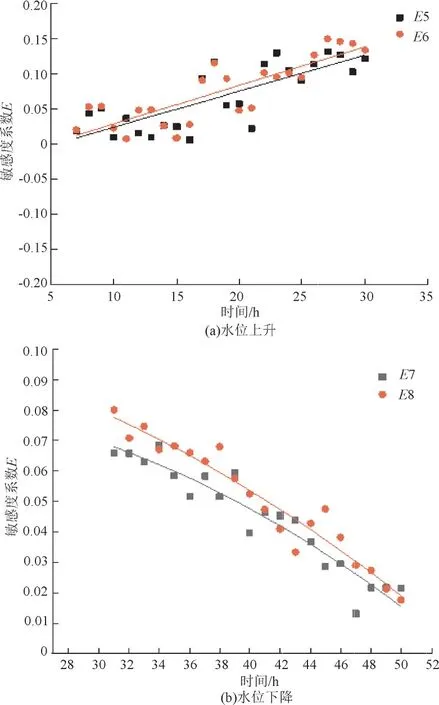
图10 地下水位波动敏感度系数分布

综合图8～图10 可知，敏感度系数E1、E2＞E6、E5＞E7、E8＞E3、E4，故对NAPL相质量溶出速率影响的因素对比如下：每增大一倍地下水流速率＞地下水位每上升0.05 m＞地下水位每下降0.05 m＞LNAPL的泄漏强度每增大一倍。

从表3 中的拟合模型表达式可以看出，地下水位下降的敏感度最符合线性规律，即地下水位下降的程度与溶出质量近似线性负相关关系；其次是地下水位上升的敏感度，也比较符合线性规律，即地下水位上升的程度与溶出质量近似线性正相关关系；而地下水流速和泄露强度的敏感度的非线性规律较强，都是先上升后下降。

3 结语

（1）LNAPL 的NAPL 相达到稳定状态时，地下水流速率与溶解速率呈现正相关趋势；泄漏速率与NAPL相饱和度呈现反相关，NAPL相饱和度与溶解速率呈现正相关，NAPL 相饱和度对研究溶解速率变化起关键作用。

（2）影响LNAPL 溶解速率因素比较结果：地下水流速率每增加1 m/s 的溶解速率变化值＞地下水位每上升1 m 的溶解速率变化值＞LNAPL 的渗透速率每增加1 kg/s 的溶解速率变化值＞地下水位每下降1 m的溶解速率变化值。

（3）对于地下水流速率较快与经常造成地下水位上升的污染源区，质量溶出效率较高，造成溶解相扩散面积大，污染羽范围广。而对于渗透速率较快的污染源区，LNAPL 的NAPL 相进入潜水面附近较多，污染源区范围大，后期也会造成溶解相的增多。因此，对于地下水流速率较快与经常造成地下水位上升的污染源区，应当格外注意扩大液相的监测，对于渗透速率较快的污染源区，应当注意排查LNAPL的NAPL相。