基于多目标优化的燃料电池汽车实时能量管理策略

于坤杰, 王思雨, 杨 朵, 符汉文, 廖粤峰

(郑州大学 电气与信息工程学院,河南 郑州 450001)

为了实现“碳达峰”和“碳中和”战略目标,构建新能源占比逐步提高的能源系统成为未来重大发展方向。在交通领域,燃料电池汽车代替传统内燃机汽车成为实现这一战略目标的有效途径[1]。

然而,燃料电池在汽车行业的应用也存在一些问题。燃料电池的动态响应比较缓慢,且无法回收车辆制动产生的能量,因此,将燃料电池和其他储能元件混合使用成为更好的选择[2]。常见的混合能源有“燃料电池+锂电池”、“燃料电池+超级电容+锂电池”以及“锂电池+超级电容”[3]。混合动力系统的关键问题在于如何分配不同能源之间的能量。目前,国内外诸多科研机构与研究团队对燃料电池的能量管理策略(energy management strategy, EMS)进行了深入的研究,其内容大致分为两类,一类是基于规则的EMS,另一类是基于优化的EMS。基于规则的EMS能够根据专家经验和操作知识,设计功率分配规则,使得燃料电池尽可能在高效率区间运行,主要包括模糊逻辑[4-5]、小波变换[6]、有限状态机[7]等,但在未知道路环境缺乏适应性。基于优化的EMS将氢耗和电池耐久性等多项指标作为目标函数,通过优化算法对目标进行优化,进而达到较优的功率分配性能,可分为全局优化和瞬时优化。全局优化方法主要包括动态规划法(DP)[8-9]、遗传算法[10-11]、粒子群优化[12]等一些其他的元启发式算法。例如,Hassan等[13]提出了改进的白鲸算法,将其应用于大规模电力系统的经济负荷调度问题。Pan等[14]提出了基于模糊逻辑和灰狼算法的EMS,通过分析驾驶行为和环境因素来预测未来的驾驶情况。然而,基于全局优化的EMS存在计算量大、难以实际应用等问题。瞬时优化方法能够在采样周期内进行实时寻优,相比于全局优化方法具有计算量较小、实时性更高等优点。Zhang等[15]提出了一种基于等效氢耗量最小原则的功率分配策略,能够有效优化驾驶性能,提高经济性。Shen等[16]和Nie等[17]采用模型预测控制方法进行混合动力系统的能量调度,验证了算法的经济性能。混合动力系统的性能受制于复杂随机的环境工况,因此,实时功率分配策略的设计难点在于如何针对不同的负载场景,提升算法的自适应能力,并实时、快速地给出最佳分配规则。

为了解决上述问题,本文将规则策略与优化算法相结合,提出了一种混合型的优化策略来解决多目标多约束下的能量管理问题。本文的主要研究贡献如下。

(1)根据燃料电池的效率特性,提出了一种基于规则的多模式能量管理策略,该策略能够使燃料电池长时间运行在高效率区。

(2)为了降低系统的氢耗量并且延长燃料电池使用寿命,基于多目标白鲸优化算法(MOBWO),对规则策略的控制参数进行优化。多目标白鲸优化算法是一种新型的基于群体的元启发式算法,相较于其他常用的多目标优化算法[18-19],在开发性能、探索能力及避免局部最优方面更加优异[20]。

(3)提出了一种数据驱动的道路工况分类方法。利用典型路况数据集和长短期记忆网络(LSTM)对驾驶路况进行分类。

(4)对测试路况进行实时分类,根据路况种类进行实时功率分配,并通过实验对比验证了所提方法的优越性。

1 系统结构和建模

1.1 系统拓扑结构

本文采用的是最常见的半主动式的混合能源拓扑结构,如图1所示[21]。锂电池直接与母线相连,减少中间能量的损失。此类结构使锂电池电压与母线电压保持一致,又能通过单向DC/DC变换器控制燃料电池的输出电流。

图1 半主动式拓扑结构

1.2 车辆动力学模型

基于车辆的纵向动力学模型,车辆牵引力Ft通过式(1)计算:

(1)

式中:m为车辆质量,kg;f为车辆与地面的滑动摩擦力系数;a(t)为行驶时的加速度,m/s2;v为车辆速度,m/s;θ为道路坡度;CD为迎风阻力系数;A为迎风面面积,m2。模型参数及取值如表1所示[22]。

表1 车辆模型参数

总线上的负载功率与牵引力和车辆速度相关:

Pm=ηFt·v。

(2)

式中:η为车辆传动系统的效率。总线负载需求、燃料电池功率及锂电池功率关系如下所示:

Pm=Pfc·ηDC/DC+Pb。

(3)

式中:Pfc为燃料电池输出功率,W;ηDC/DC为DC/DC转换器效率,取0.95;Pb为锂电池输出功率,W。

1.3 燃料电池模型

本文采用的是由330个质子交换膜燃料电池单体串联而成的燃料电池系统,最大输出功率为50 kW。由于燃料电池在整个运行系统中提供稳定的输出功率,进而忽略燃料电池的动态响应,只考虑用静态模型来描述燃料电池特性。其电堆功率与系统的输出功率有如下关系:

Pfc=Pst-Paux。

(4)

式中:Pfc为燃料电池系统的净功率,W;Pst为燃料电池电堆产生的功率,W;Paux为辅助系统消耗的总功率,包括空气压缩机、水泵等,W。

燃料电池的氢气消耗量与电流成正比。如式(5)所示:

(5)

式中:N为燃料电池的数量;MH2为氢气的摩尔质量,g/mol;n为反应时转移的电子数量;F为法拉第常数。

此外,净输出功率与氢气产生的总功率的比值可以用来定义燃料电池系统的输出效率:

(6)

式中:LHV表示氢气的低热值。燃料电池的效率和净功率关系如图2所示。

图2 燃料电池功率-效率图

燃料电池在使用过程中会逐步老化,根本原因是电池内部的温度、湿度和压力的变化,进而导致催化剂失活、膜老化、电解质受污染和材料腐蚀等。对于混合动力汽车来说,车辆的启停、负载变化、怠速及加速都会造成燃料电池不同程度的老化。本文采用Yue等[23]提出的燃料电池老化数学模型衡量其老化程度,如式(7)所示:

(7)

式中:p为最大允许衰减比例;kp为修正系数;p1、p2、p3、p4分别为启停、加速、怠速、负载变化的衰退速率;n1、n2、t3、t4分别表示启停次数、加速次数、怠速时间、负载变化时间。各个参数的值如表2所示。

表2 衰退率参数

1.4 锂电池模型

本文采用的是由100节磷酸铁锂动力电池串联而成的电池组,端电压在330 V左右。所采用的模型是高精度的R-int等效电路模型,如图3(a)所示。其中,锂电池电流为

(8)

图3 锂电池模型

式中:UOCV为锂电池开路电压,V;Rb为锂电池内阻,Ω;Pb为燃料电池的输出功率,W。锂电池的另一个重要指标为锂电池的荷电状态SOC,如式(9)所示:

(9)

式中:Q为锂电池容量,Ah,本研究中使用的电池容量为10 Ah。锂电池的SOC和UOCV的关系如图3(b)所示。

1.5 等效氢耗模型

本文考虑到燃料电池汽车在行驶途中会向锂电池输送能量,如果仅计算燃料电池的氢耗量而不考虑锂电池在驾驶工况前后SOC的差值,整个混合系统的消耗成本会有误差。系统的等效氢耗量模型如式(10)和(11)所示:

(10)

mH2=mfc+mb。

(11)

式中:mb为锂电池的等效氢耗;mH2为整个系统在运行时间内的等效氢耗量,g;nb为锂电池个数;ηfc,avg为燃料电池在工作区间内的平均效率。

2 能量管理策略

2.1 基于规则的功率分配

本文根据车辆在驾驶过程中存在的几种工作模式,设计了一种基于规则的功率分配策略。

(1) 启动模式。需求功率未达到燃料电池的最小功率,且锂电池SOC未达到设定上限时,燃料电池以最小功率运行,锂电池吸收多余能量;当SOC达到设定上限,多余的能量由车辆的制动电阻消耗。

(2) 节能模式。需求功率未达到燃料电池的效率最高点且锂电池SOC未达到设定上限时,燃料电池工作在最高效率点,多余的能量由锂电池吸收;当锂电池的SOC达到设定上限后,燃料电池以最小功率运行,锂电池补充剩余功率。

(3) 低功率模式。设定燃料电池工作点1。当车辆需求功率未达到工作点1,且锂电池SOC未达到设定下限时,燃料电池工作在工作点1,锂电池吸收多余能量;当SOC随着充电达到设定下限时,燃料电池以最高效率点时的功率与工作点1之和的k倍运行;当SOC随着充电达到设定值SOC1时,燃料电池工作在最高效率点;当锂电池的SOC随着充电达到设定上限时,燃料电池以最小功率运行,不足的能量由锂电池补足。

(4) 中低功率模式。设定燃料电池工作点2,SOC设定值SOC2。车辆需求功率未达到工作点2且SOC未达到设定下限时,燃料电池工作在工作点2,工作规则与低功率模式相同。

(5) 中高功率模式。设定燃料电池在此模式下工作点为最大功率点,SOC设定值SOC3。车辆需求功率未达到燃料电池最大功率且SOC未达到设定下限时,燃料电池以最大功率运行,工作规则与低功率模式相同。

(6) 高功率模式。车辆需求功率达到燃料电池的最大功率,锂电池SOC达到设定下限时,燃料电池以最大功率运行,锂电池不提供能量,此时提供的能量不足以满足需求功率;当SOC未达到设定下限时,燃料电池以功率点2与最大功率之和的k倍运行,不足的能量由锂电池提供;当SOC达到设定上限时,燃料电池以最小功率运行。

工作流程如图4所示。根据图4计算出燃料电池的输出功率,进而通过式(3)推出锂电池所需输出功率。

图4 基于规则的功率分配策略流程图

在该策略下,燃料电池有多个工作点。当SOC值处于正常区间且较小时,燃料电池提供尽可能多的能量,以应对后续可能会出现的大功率阶段。当SOC值处于正常区间且较大时,锂电池提供尽可能多的能量,以防止后续可能会出现的制动状态,导致锂电池过饱和。此外,燃料电池输出功率的变化率对其寿命有着非常重要的影响,因此,本研究将燃料电池的最大变化率设定为5 kW/s,以降低燃料电池的寿命损耗。

2.2 多目标白鲸优化算法

为了降低系统氢耗并延长燃料电池寿命,用MOBWO进行EMS参数优化。该算法受到白鲸行为启发,建立了探索、开发及鲸鱼坠落3个阶段。

探索阶段是通过人类饲养白鲸的行为记录建立的。2只白鲸可以以同步或者镜像的方式游泳。因此,白鲸的位置更新为

(12)

开发阶段受到白鲸捕食行为的启发,白鲸通过分享彼此的位置信息来捕食,同时考虑捕食的最佳位置信息和其他白鲸位置信息。在开发阶段引入了Levy飞行策略,以便于增强收敛性。其数学模型为

(13)

式中:r3、r4为(0,1)内的随机数;C1为衡量Levy飞行强度的随机跳跃强度;LF为Levy飞行函数,其数学公式为

(14)

式中:u和v为正态分布的随机数;β取1.5;参数σ为

(15)

鲸落阶段是考虑到白鲸在迁徙和觅食的过程中,少数白鲸收到自然界的威胁而死亡。其数学模型为

(16)

式中:r5、r6、r7均为(0,1)内的随机数;Xstep为鲸鱼坠落的步长,公式为

Xstep=(ub-lb)exp(C2T/Tmax)。

(17)

式中:C2为步长因子,与鲸鱼坠落概率和种群规模相关;ub和lb分别为变量的上边界和下边界。

2.3 基于白鲸优化的能量管理策略

本文使用白鲸优化算法对2.1节提到的基于规则的功率分配策略进行参数优化。其中,决策变量Xi=[Pfc1,Pfc2,Pfcmax,SOC1,SOC2,SOC3,k],目标函数分别为等效氢气消耗量和燃料电池的老化百分比:

(18)

算法中的参数设置如表3所示。

表3 白鲸算法参数

3 基于LSTM网络的实时路况分类

驾驶路况判别是一个典型的分类问题,根据特定时间段的车速情况,可以将驾驶路况分为高速路况、畅通路况和拥堵路况。为了设计高精度的分类器,分别使用标准化城市驾驶工况(UDDS)、洛杉矶路况(LA92)及季节性制冷能效比路况(SC03)作为畅通路况集,曼哈顿城市路况(MANHATTAN)、城市拥堵路况(NYCC)作为拥堵路况集,主干线和高速行驶路况(US06)、未被空调满负荷循环覆盖的车辆工况循环(REP05)及美国乘用车高速公路燃油经济性测试工况(HWFET)作为高速路况集[24]。

本文使用LSTM神经网络来训练驾驶路况分类器的模型[25]。LSTM被认为是循环神经网络(RNN)的变体,一般用来解决时间序列问题。其工作原理如图5所示,A表示单个LSTM网络,LSTM将输入序列x分成若干个时间步,每个时间步输入一个向量,并根据当前的输入以及前面所有时间步的状态,计算出当前时间步的输出y。LSTM中的2个基本单元是记忆单元和门控单元。尽管LSTM比RNN网络更加复杂,但是其门控单元使该网络处理时间序列的效果更好。

图5 LSTM工作原理图

本研究使用窗口大小为60 s的滑动窗口对不同驾驶路况的速度曲线取值,取得的一系列数据作为训练集。标签1为畅通路况、标签2为拥堵路况、标签3为高速路况。在对上述3种驾驶路况进行LSTM网络训练后得到驾驶路况分类器。其训练结果如图6所示。由图6可知,在训练1 000次之后,准确度收敛至99.5%,满足使用要求。

图6 LSTM神经网络模型训练图

4 实验结果与分析

图7展示了本文所提的EMS算法框架。首先,对燃料电池和锂电池进行离线测试,从而获得关键参数并以此建立数学模型。其次,通过大量离线数据库建立多目标优化策略和路况分类器,所提策略在MATLAB 2021b上实现。最后,通过获取实时驾驶数据来进行路况分类,并根据分类标签更新对应的控制参数。本文算法基于MATLAB/Simulink平台开发,在优化好控制器参数后,利用硬件在环仿真平台进行算法验证,平台架构和设备参数如图8所示。其中,实时仿真设备用于模拟混合动力系统的实际运行情况,并与EMS控制器进行实时通信,在上位机界面监控系统运行结果。

图7 所提EMS算法框架

图8 平台架构和设备参数图

4.1 多目标优化结果

为了验证所提策略的有效性,利用3种不同路况数据进行仿真。经过白鲸算法优化参数后得到3组帕累托前沿,如图9所示。在帕累托解中利用权重法和可行性法则共同挑选一组合适的最优解作为基于功率分配的可变参数,如表4所示。进而,在该组参数下燃料电池与锂电池的功率分配和SOC变化如图10所示。由图10可知,燃料电池能够较平稳地输出功率。锂电池提供峰值功率并及时吸收制动产生的能量,锂电池的SOC在安全范围内波动。

表4 多目标白鲸算法优化后的参数值

图9 3类路况下的帕累托前沿

图10 功率分配图和SOC变化图

4.2 基于LSTM分类器的实时功率分配策略

进一步,为了研究所提方法的路况适应性,利用全球轻型汽车排放测试工况(WLTC)作为测试工况。在每个行驶时刻采用其前60 s的速度值作为LSTM分类器的输入,输出则为标签的预测值。分类结果如图11中黑色数字标签所示,在0～77 s时属于畅通路况,78～244 s时属于拥堵路况,245～1 627 s时属于畅通路况,1 628～1 801 s时属于高速路况。

图11 WLTC功率分配图

图11和图12分别展示了在WLTC路况下的基于多目标优化和路况分类的功率分配结果和锂电池的SOC变化曲线。从图12中可以看出,基于多目标和路况分类的EMS能够实时改变控制参数,以应对驾驶路况的改变。

图12 WLTC工况下的SOC

为了展示所提方法的优越性,通过几组与未优化前的EMS结果进行了对比分析,对系统的等效氢耗与燃料电池寿命衰减进行了量化计算。表5展示了在WLTC工况下几种不同EMS的氢气消耗量和老化程度。其中,基于规则1、2、3表示根据设计者经验选取控制参数不同时的多模式功率分配策略。其决策变量分别为[12 000 35 000 50 000 0.5 0.5 0.5 0.5]、[12 000 35 000 45 000 0.5 0.4 0.4 0.5]、[20 000 40 000 50 000 0.5 0.5 0.5 0.67]。

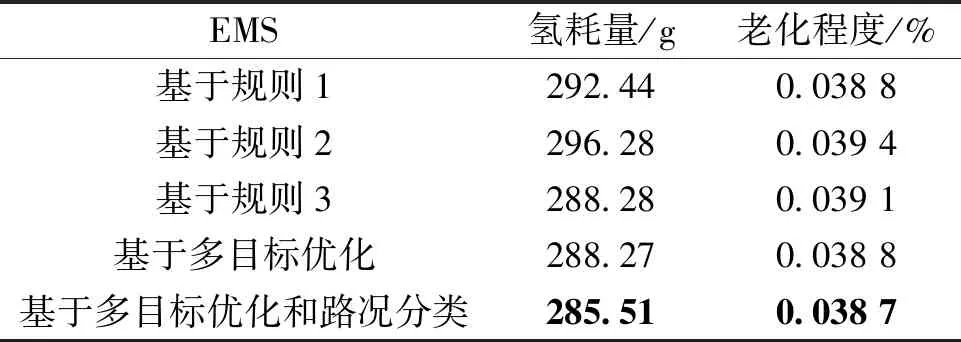
表5 不同EMS的氢耗量和老化程度

从表5可以看出,基于规则的控制参数取值的不同决定了EMS性能差异,需要依靠设计者经验来获得最好的效果。基于多目标优化的EMS,针对单一路况能够依据对氢气消耗量和老化程度侧重点的不同而选取最佳参数值,进而得到符合自己预期的效果,基于多目标优化与基于规则1、2、3的均值相比,氢耗量降低了1.4%,老化程度降低了0.77%。基于多目标优化和路况分类的EMS能够随着路况的改变而改变功率分配的控制参数,从而适应于不断变化的路况,基于多目标优化和路况分类与基于规则1、2、3的均值相比,氢耗量降低了2.3%,老化程度降低了1.02%。

5 结论

(1)针对混合动力系统能量管理问题,提出了一种基于多目标优化和路况分类的EMS。该策略引入等效氢耗模型和燃料电池的老化模型,并使用白鲸多目标优化算法对功率分配策略的控制参数进行优化。为了解决该策略不具有普适性的问题,引入了 LSTM神经网络对驾驶路况进行分类。

(2)通过对3类经典路况训练后得到了路况分类模型,用此模型将复杂测试路况分解成经典路况,并在不同路况下实时转换功率分配的控制参数,以达到最优效果。实验结果表明,与未加入多目标优化和路况分类的策略相比,所提出的EMS具有较好的经济性和耐久性,并且能够实时改变策略以应对变化的路况。

(3)混合动力系统的能量管理问题目前仍是一个较难的领域。所提出的EMS虽然表现出了良好性能,但是基于功率分配的EMS的局限性依旧存在。如何平衡车辆的动力性能、燃油经济性和动力元件的耐久性是未来一个重要的研究方向。