外包钢壳混凝土异形索塔及其施工临时支撑研究
陈逸君,黄文金*,王志福,刘君平
(1.福建农林大学 交通与土木工程学院,福建 福州 350108;2.福建第一公路工程集团有限公司,福建 泉州 362100;3.福州大学 土木工程学院,福建 福州 350108)
市政桥梁作为城市重要的标志性建筑之一,在结构选型时往往倾向于造型优美的斜拉桥。斜拉桥索塔既是主要承重构件,又是建筑美学的表现主体,故许多斜拉桥索塔基于景观设计要求而采用倾斜的异形结构。为了确保施工安全和质量,并控制异形索塔的现场施工进度及成本,宜采用少支架的临时支撑方案。因此,外观质量好、施工便捷的外包钢壳混凝土索塔应运而生[1]。然而,异形索塔在施工过程中的受力体系、荷载类型及大小都将发生剧烈变化,须严格控制索塔及其支撑体系的应力和变形状态。
对于钢筋混凝土异形索塔,学者们依托实际工程通过实验和有限元分析对其临时支撑体系的设计、优化和比选进行研究[2-5]。而钢壳混凝土索塔作为一种特殊的结构形式,学者们的研究主要是针对该类索塔的施工技术和受力情况。叶伟等[6]通过非线性有限元对外包钢板混凝土索塔的力学性能进行了分析。彭强[7]和陈平等[8]通过足尺模型试验研究了外包钢壳混凝土索塔的工艺流程和钢壳制造关键技术。樊健生等[9]对钢板-混凝土组合结构桥塔的受力机理、设计理论及工程应用的国内外发展状况进行了对比分析。但目前对于异形钢壳混凝土索塔的有限元建模方法及临时支撑方案的研究则相对较少。为确保此类型索塔的施工安全和质量,以于都大桥为工程背景,设计了三种临时支撑方案,并建立不同的有限元计算模型,分析支撑方案在施工过程中对外包钢壳混凝土索塔应力及变形的影响,以期对类似索塔及其支撑方案的设计与施工提供借鉴作用。
1 工程概况
于都大桥索塔横桥向采用“鱼跃”造型的异形拱,索塔包括下塔柱、下横梁、上塔柱三部分,见图1。支撑杆1—4为施工索塔时的临时水平钢管支撑。索塔下横梁采用箱形截面。在塔底处,两塔柱外缘横向间距为40 m,向上逐步外倾,在塔柱弧段理论分界处(Ⅲ-Ⅲ截面)达到最大值42 m,随后向上逐步呈拱形内敛,塔柱轴线在Ⅲ-Ⅲ截面以下为圆弧,以上为椭圆。索塔截面顺桥向采用等宽度4.5 m;横桥向不等宽,在塔底为8.5 m,在Ⅲ-Ⅲ截面处为最小值4 m,在塔顶为7 m,其间匀顺变化。索塔钢壳从下往上分为T0—T19共20个施工节段,采用先塔后梁的顺序施工,具体施工步骤见表1。表1中,CSi表示施工阶段i(i=1,…,23),T0为塔底连接段,T2为下横梁节点处塔柱节段,T19为塔顶合龙段,L0为下横梁连接段。

图1 索塔及其支撑布置方案(单位:cm)

表1 索塔施工阶段编号及安装部件
索塔为实心截面,其中塔身外包钢壳由外包钢板、环向加劲肋、内角钢拉杆以及节点板构成,见图2。钢壳采用Q345 D级钢材,钢壳内浇筑C50混凝土。

图2 索塔节段钢壳构造图
2 建模方法
对于索塔梁单元模型,采用Midas Civil软件建模。因塔柱钢材与混凝土尺寸在塔柱截面上相差很大,故钢壳混凝土塔柱采用双单元法模拟。在承台处对索塔单元进行固结,并根据上述施工步骤将施工阶段划分为23个。
对于壳-实体单元模型,采用Midas FEA NX软件建模,如图3所示,图中蓝色表示混凝土,玫红色表示钢壳,灰色表示钢壳拉杆及加劲肋。采用壳单元模拟索塔外包钢壳,采用实体单元模拟混凝土、下横梁及索塔支撑杆。不考虑腔内混凝土和钢壳的脱黏行为,以提高计算稳定性和分析效率。塔柱钢壳单元和腔内混凝土单元在界面处共用节点,并模拟有无钢壳内拉杆和加劲肋连接的两种状态。网格采用尺寸控制与自动生成技术相结合的方法进行划分。

图3 壳-实体单元模型
作用在索塔及其支撑体系的荷载有结构自重、风荷载和施工荷载。按《公路桥梁抗风设计规范》[10]计算的索塔基准高度处横桥向风荷载为10.2 kN/m;施工荷载为2.5 kN/m2。
3 支撑方案比选
3.1 支撑方案设计
塔柱在合龙前处于悬臂柱受力状态,若不设置索塔临时支撑,塔柱横桥向侧移将达塔高的1/367,并使得其根部和弧段理论分界处存在很大拉应力,不满足规范[11]对施工安全质量方面的要求。故综合考虑裸塔状态下的应力变形规律、节段划分及施工空间等因素后,共设计了三种支撑方案,见表2。
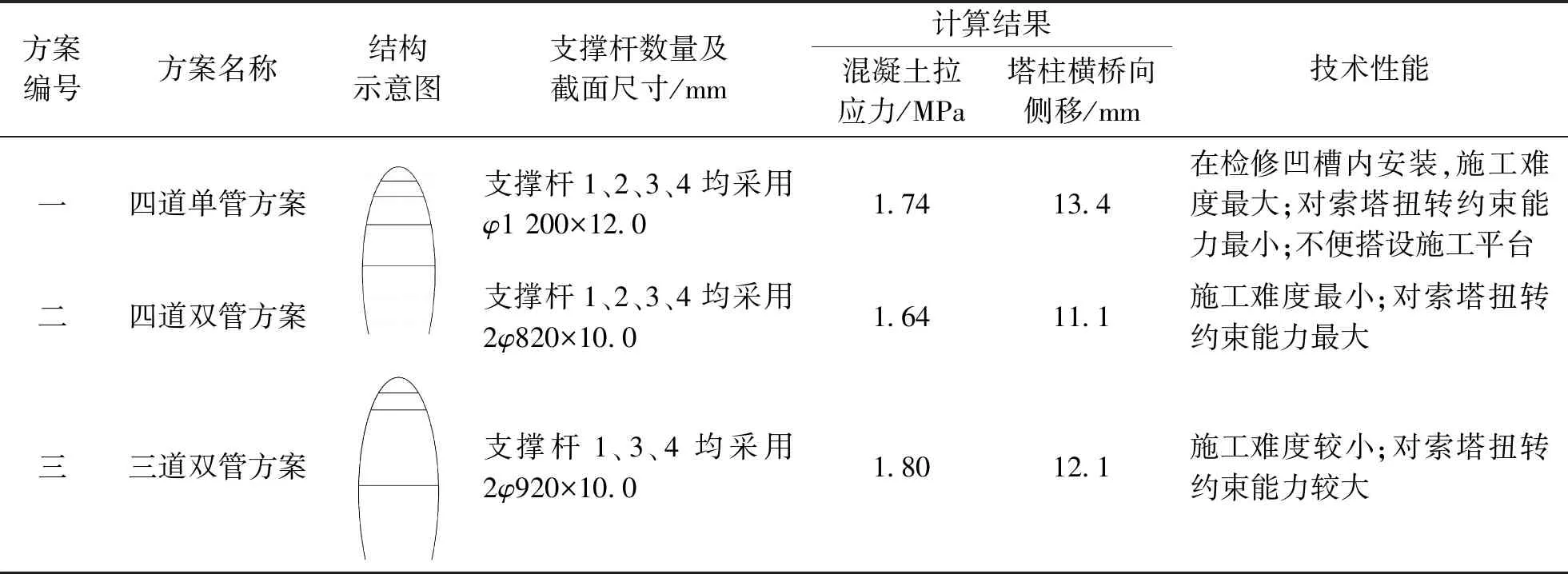
表2 临时支撑方案设置及计算结果
单管或双管支撑方案的平面布置形式见图4。对于双管支撑方案,两根钢管的纵桥向轴线中心距为3 m。安装钢管支撑时,采用牛腿垫块和纵桥向安装限位块进行定位,以确保施工安全及支撑杆焊接精度。平联杆采用H型钢。钢管支撑杆合龙处采用对接剖口焊并采用纵向加劲肋进行补强。

图4 塔柱支撑杆平面布置示意图
3.2 不同支撑方案的索塔应力及变形
3.2.1 变形
施工时塔柱变形差过大会导致下一节段钢壳焊接困难、影响施工质量,故在施工过程中,应对塔柱坐标及高程进行实时监控。
三种方案的变形模式类似,见图5,塔柱变形均控制在15 mm(H/6 000)以内,均能满足施工要求。在合龙前塔柱最大变形位于其悬臂端。塔柱变形随着节段浇筑高度的增加而增大,从施工阶段CS12开始,由于塔柱的拱形轴线越来越弯曲,故塔柱因弯曲变形引起的横向侧移和竖向挠度随之显著增大。在合龙后,即从施工阶段CS21开始,塔柱已形成拱形结构,即便拆除支撑杆,塔柱的横向弯曲刚度也大于合龙之前的,因此由风压等非对称荷载引起的塔柱横桥向侧移开始减小。由此可见,施工时应密切监测塔柱变形尤其是横桥向侧移,保证塔柱线形与设计线形一致,同时在合龙前还需严格控制合龙温度和横桥向非对称荷载,以确保索塔顺利合龙。
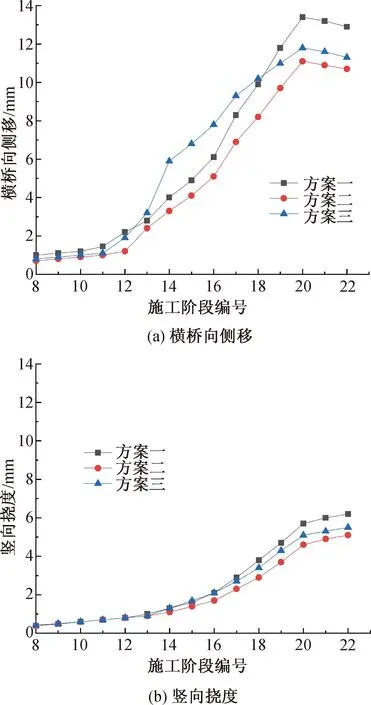
图5 塔柱顶端变形
此外,对于方案三,从施工阶段CS12开始,由于不设支撑杆2,悬臂弯曲塔柱的变形尤其是横桥向侧移将迅猛增大,既增大塔柱的钢壳安装误差和线形控制难度,又降低焊缝质量,甚至引发施工安全事故。因此,在施工中,应注意横桥向侧移的监控。特别值得一提的是,合龙后索塔的最大变形位置将由合龙前的悬臂端变化到Ⅳ-Ⅳ截面附近,因此应密切监测支撑杆3的轴力和接头安装质量。
3.2.2 应力
上述塔柱变形分析表明,在安装塔柱钢壳和浇筑腔内混凝土时塔柱将发生较大的弯曲变形。裸塔状态下(无支撑)塔柱在Ⅳ-Ⅳ截面将发生很大的横桥向侧移,塔柱根部和弧段理论分界处即Ⅰ-Ⅰ和Ⅲ-Ⅲ截面的混凝土将承受很大的竖向拉应力,导致混凝土开裂。设置支撑后,支撑将限制塔柱的横桥向侧移,使得混凝土拉应力显著减小,尤其是Ⅲ-Ⅲ截面,各支撑方案的混凝土拉应力均控制在1 MPa以内。对于Ⅰ-Ⅰ截面,支撑对混凝土拉应力的减小作用小于Ⅲ-Ⅲ截面,混凝土拉应力在索塔的整个施工过程中都在增大,见图6。
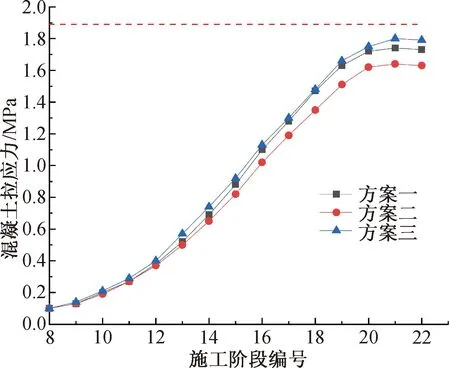
图6 塔柱混凝土拉应力
如图6所示,三种支撑方案的塔柱混凝土拉应力变化规律大体相似,施工到CS20(索塔合龙)后拉应力不再大幅变化。在CS16时,塔柱腔内混凝土拉应力超过1 MPa,此后逐渐逼近C50混凝土抗拉强度设计值即1.89 MPa,因此从CS16到CS20应重点监控Ⅰ-Ⅰ截面的混凝土拉应力,防止混凝土开裂。
支撑杆也可以显著减小塔柱的压应力,尤其是对于压应力最大的“悬臂柱”底端Ⅰ-Ⅰ截面。以塔柱应力最大的支撑方案一为例,该截面混凝土以及钢壳的最大压应力分别为8.2 MPa和119.1 MPa,与未设置支撑的裸塔状态相比分别减少了70%和63%。
3.2.3 风荷载作用分析
在索塔结构合龙前,横桥向风荷载将进一步加大索塔横桥向侧移和腔内混凝土竖向拉应力。不同风速下塔柱的横桥向侧移见图7,图中的横坐标为按照规范[10]依据设计基准风速Ud计算得到的索塔基准高度处的等效阵风风速Ug。
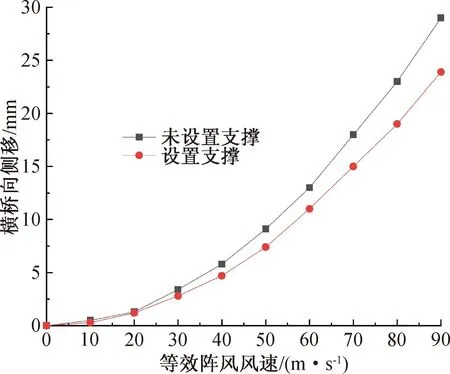
图7 不同风压下的塔柱变形
由图7可知,塔柱横桥向侧移随风速增大呈二次抛物线显著增大,而支撑可显著约束风压下的塔柱变形。当等效阵风速度达到40 m/s时,设支撑前后索塔横桥向侧移分别为5.8、4.7 mm,支撑将减小23%的塔柱横桥向侧移。
由于索塔横桥向侧移将在腔内混凝土中引起竖向拉应力,当风速较大时可能导致混凝土开裂。不同风速引起的腔内混凝土竖向拉应力见图8。如图8所示,对于最低基本风速24.5 m/s即等效阵风风速34 m/s,腔内混凝土竖向拉应力达到0.5 MPa。因此,在设计和建模验算时应充分考虑风荷载对索塔结构的影响,在施工时应采取抗风措施以减少风荷载引起的索塔变形和混凝土拉应力。

图8 不同风压下的塔柱混凝土拉应力
3.3 支撑杆的应力、变形及稳定性
支撑杆在施工中将承受较大的应力和变形,为防止支撑杆发生破坏,保证索塔施工安全,除了分析验算塔柱外,还需对支撑杆的应力、变形及稳定性进行验算。
3.3.1 变形
支撑方案二的支撑杆轴向变形最小,其最大压缩变形出现在支撑杆4为7.1 mm,最大拉伸变形出现在支撑杆1为9.3 mm。对于支撑杆4即塔柱最后一道支撑杆,施工过程中需对其长度加工精度和节点连接质量进行严格控制,以保证索塔顺利合龙。
对于支撑杆最大竖向挠度,均出现在索塔合龙阶段。其中,靠近塔底的支撑杆1变形最大,支撑方案一、二、三的计算值分别为37.6、29.1、31.2 mm,均小于47.4 mm(l/400,l为支撑长度),其竖向挠度符合规范要求。
3.3.2 应力及稳定性验算
未合龙前塔柱为弯曲悬臂柱,其受力状态见图9。如图9(a)所示,因该阶段塔柱的重心位于塔柱根部截面重心外侧,支撑杆1需提供拉力F以平衡重力G1引起的逆时针弯矩M,随着塔柱节段的内倾,负偏心距e逐渐减小,导致支撑杆1所受拉力逐渐减小;但是,后续安装的支撑杆2—4协助支撑杆1抑制塔柱内倾,使得支撑杆1拉力变化有限,在整个施工过程中始终承受拉力。对于四道支撑方案的支撑杆2,如图9(b)所示,因塔柱悬臂段(支撑杆2之上部分)的重心位于支撑杆1与塔柱连接点的右侧,支撑杆2需提供推力以平衡顺时针弯矩M,随着塔柱节段增长,正偏心距e逐渐增大,导致支撑杆2所受压力逐渐增大;至安装支撑杆3后,支撑杆2压力减小;当索塔合龙形成拱结构时,因支撑杆2接近“拱脚”(塔柱弧段分界线),在拱的水平推力作用下,支撑杆2由受压转为受拉。同理,支撑杆3、4刚开始都是承受压力的,但在塔柱合龙后由于远离“拱脚”,故在整个施工过程中始终受压。同样地,对于三道支撑方案,其支撑杆1始终受拉,支撑杆3由安装时的受压逐渐转为受拉,支撑杆4则始终受压。因此,在施工过程中应注意监控中间支撑杆的轴力变化,并严格监控各支撑杆的接头焊接质量。

图9 支撑杆受力状态示意图
各方案支撑杆考虑稳定系数后的应力见表3,表中应力拉为正压为负。由表3可知,各支撑杆应力均小于Q235级钢材的屈服强度,满足强度及稳定性要求。

表3 支撑杆轴向应力对比 (单位:MPa)
3.4 临时支撑方案比选
上述计算分析表明,各支撑方案的塔柱及其支撑体系的强度和刚度均符合规范要求,而采用四道双管的方案二的应力和变形最小(表2),且有利于在支撑杆上搭设施工平台,故推荐采用方案二。
4 建模方法对比
本桥索塔为组合结构,且轴线为拱形,不同的建模方法对计算结果有一定影响。梁单元模型建模简单、计算快,一般用于施工验算的简单分析。但梁单元无法体现出结构相对薄弱、容易形成应力集中的局部细节。因此,本文分别采用梁单元和壳-实体单元建立设置四道双管支撑的索塔模型以对比不同建模方法。
以支撑方案二的索塔及其施工临时支撑为例,不同模型的计算结果见表4。如表4所示,对于没模拟施工阶段的模型BM1,由于忽略了塔柱合龙前的应力累加过程,因此其计算的变形比有模拟施工阶段的模型BM2的小46%~59%,应力小51%~60%。这说明对于异形钢壳混凝土索塔,分析时应模拟施工阶段,否则计算结果将有很大误差。
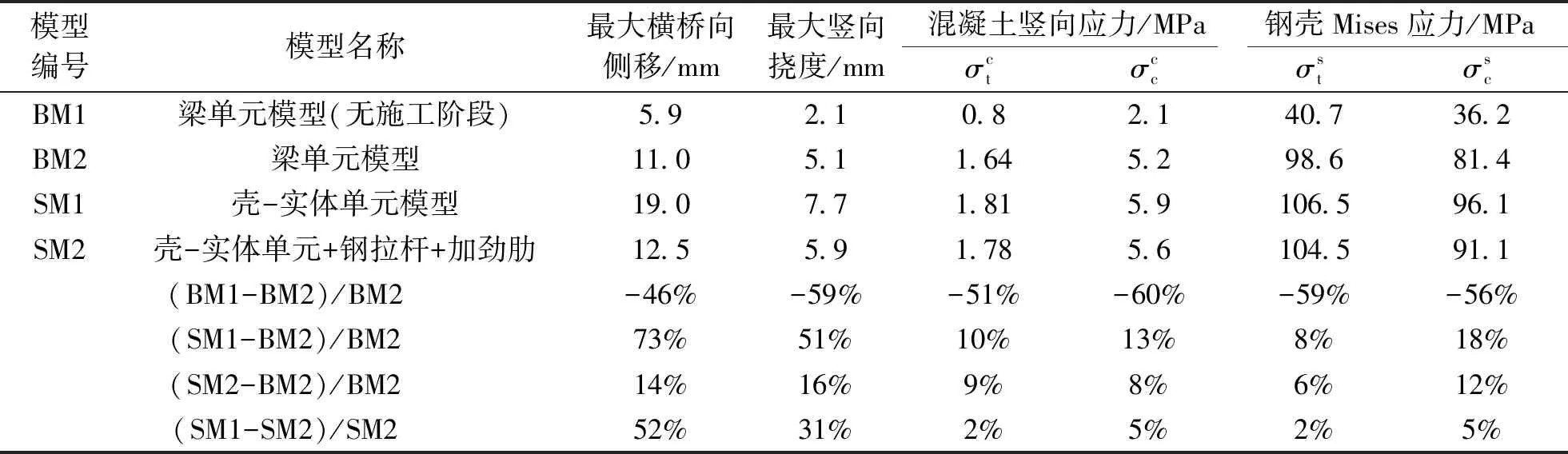
表4 不同有限元模型计算结果对比
对于没模拟钢壳内拉杆和加劲肋的壳-实体单元模型SM1,其计算的横桥向侧移、竖向挠度分别比梁单元模型BM2的大73%和51%,而钢和混凝土的应力差值仅为8%~18%。造成这种现象的原因是,BM2的钢壳在同一截面上的变形相同,而SM1没模拟钢壳内拉杆和加劲肋,导致外包钢壳变形计算结果偏大。对于有模拟钢壳内拉杆和加劲肋的壳-实体模型SM2,其计算的变形比梁单元模型BM2的大14%~16%,应力大6%~12%,差别不大。由此可见,当进行施工简单验算或无需进行局部精细分析时,可以采用考虑施工阶段的梁单元模型BM2,而当需要准确模拟局部精细分析时,如浇筑腔内混凝土阶段时的钢壳节段、检修凹槽和角点等处的应力和横断面变形,应采用模拟钢壳内拉杆和加劲肋的壳-实体单元模型。
此外,SM1计算的应力仅比SM2大2%~5%,而变形大31%~52%,说明钢拉杆和加劲肋对改善钢壳应力的作用不明显,但可以有效减小钢壳变形。因此,在实际施工中,为减小外包钢壳变形影响施工精度,应严格控制节段划分长度并及时安装钢壳内拉杆及加劲肋。
5 结论
1)索塔的拱形轴线对其内力和变形影响很大,在合龙前后索塔内力和几何状态将发生较大改变,且对横桥向荷载作用很敏感。
2)索塔支撑可显著降低塔柱变形和混凝土应力;本文提出的三种支撑方案即四道单管方案、四道双管方案以及三道双管方案,均能满足施工阶段索塔及其支撑体系的强度、刚度和稳定要求,提高索塔安装精度,其中四道双管支撑方案的综合性能最优。
3)采用有限元模拟时,应考虑非对称荷载和施工阶段划分对钢壳混凝土异形索塔整体受力变形的影响;梁单元模型能准确计算塔柱的竖向应力和整体变形;而横断面应力和局部变形分析,应采用模拟构造细节的壳-实体模型。
4)拉杆及加劲肋对减小塔柱外包钢壳变形的作用很大;吊装钢壳时应先焊接拉杆和加劲肋,并严格控制塔柱节段长度。
5)风荷载对塔柱横桥向侧移及腔内混凝土拉应力影响很大,应重视索塔抗风变形验算,并加强抗风措施。

