设计类问题解决能力的多模态表征模型与验证

武法提 王兆雪

一、引言

设计是一种创造性活动，是国家核心竞争力的重要组成部分，旨在产生创造性结果或创造性地解决问题，是实现创新的重要途径和有效方式（山丹, 2021）。21 世纪以来，设计类问题在各大领域中频繁出现，具备设计类问题解决能力可以帮助人们解决各类复杂问题与生活议题。因此，设计类问题的解决能力成为21 世纪学习者必备的关键技能。研究表明，对其进行测评，有助于面向智能时代创新型人才的培养（王兆雪& 武法提, 2022）。同时，设计类问题解决是一种协作问题解决活动。在这种协作问题解决活动中，设计思维是贯穿设计类问题解决过程的思维策略，协作交流是贯穿设计类问题解决过程的重要途径。

目前对于设计类问题解决能力测评主要基于数据驱动的多模态测评方式，这种方式可以获取全方位数据，兼顾外在行为数据与内在生理数据，是精准化测评的重要手段（胡航&杨旸,2022）。设计思维重点考察设计认知方面的情况，主要采用心理学量表、真实情景的计算机测试或多模态数据进行测评，如盖勒等（Gero&Milovanovic,2020）以设计认知为研究主题，收集学习者在设计过程中的眼动数据和情绪数据，分析生理层面的设计认知，同时收集EEG 脑电波数据、功能性近红外光谱和功能性磁共振成像数据，分析神经层面的设计认知。协作交流主要考察社会技能，如协同进行信息共享并共同完成任务的情况，主要采用社交网络特征、交互式文本分析或心率皮肤电等数据变化来测评，如格罗弗等（Grover et al.,2020）通过收集协作过程中的视频、音频、点击流和屏幕捕获数据，对合作能力进行多模态测评，最终达到44%的预测准确率。施奈德等（Schneider&Blikstein,2014）利用双手协调数据、身体同步数据和身体距离数据来评判学习者的协作学习结果。

为了实现精准化的设计类问题解决能力测评，如何将多种来源、通道和场景的数据进行融合是目前多模态学习分析的难点（彭红超&姜雨晴,2022）。在高阶能力测评研究中，多模态数据融合主要有三种方法：1）数据融合，将多个模态的数据融合成单一的特征矩阵，输入机器学习的分类器中进行训练（王一岩&郑永和,2022）；2）特征融合，提取数据特征，并基于这些特征规则进行融合（Majumder et al.,2018）；3）决策融合，也是能力测评中最常用的一种数据融合方案，先对每个模态的数据单独进行处理、训练和判断，最后对所有决策结果进行融合（丁继红, 2023）。决策融合的优势在于需要融合的数据来自不同的数据分类器或模态结果，每个模态的数据之间互不影响，可单独计算，错误不会累计。三种方法各有利弊，但在设计类问题解决能力的测评中，不同融合方式的效果还需要探索。

因此，本研究对学习者在设计过程中的全过程数据进行记录与分析，并运用恰当的算法分析交叉验证设计类问题解决能力各维度的状态，对设计类问题解决能力进行多模态数据表征，从而打开设计的“黑箱”，为设计类问题解决能力测评提供更加精准的方法，为培养学生的创新能力提供支撑。

二、多模态数据表征的设计类问题解决能力测评模型实证分析

（一）测评模型构建

本研究试图剖析设计类问题解决能力的关键要素，通过采集学习者在设计类问题解决过程中的多模态数据，对设计类问题解决能力进行多模态数据表征，为其个性化、精准化测评提供新的解决方案。王兆雪和武法提（2022）在关于设计类问题解决能力的研究中，从认知与协作两个维度进行分析，提出“设计思维是贯穿设计类问题解决过程的思维策略与协作交流，是贯穿设计类问题解决过程的重要途径”两个重要观点，并将其划分为反思调节、观点建构、组织协调和同理心四个子维度。本研究对上述设计类问题解决能力多模态测评框架进行修改与完善，通过采集心理量表、生物传感数据和行为言语数据，构建了多模态数据表征的设计类问题解决能力测评模型，如表1所示。

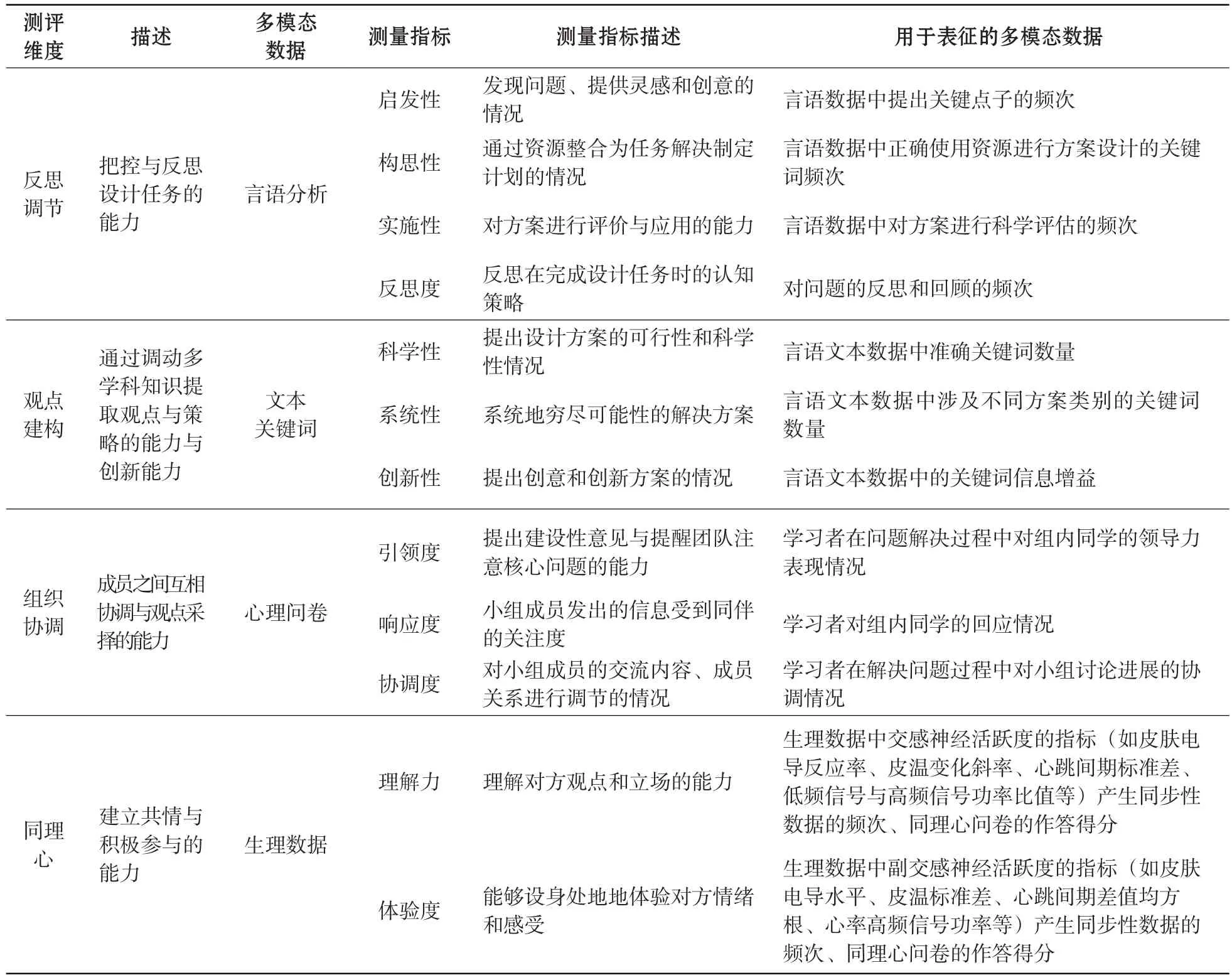
表1 多模态数据表征的设计类问题解决能力测评模型

（二）实验设计与数据采集

实验在北京师范大学多模态学习分析实验室中展开，被试为校内学生。首先进行预实验，随机召集被试三组，共9人，年龄为18—22 岁。预实验的目的主要是对实验设备的有效性、学习任务和学习支架的可靠性进行检验。正式实验选取被试181人，3—4人一组进行实验，要求学习者在给定空地上建造一个合理用水的生态海绵校园。主试在后方全程监督，在不干扰被试的前提下确保被试顺利完成学习任务。

在学习者完成设计的过程中，主试进行问题解决全过程的数据采集，包括会话文本数据、心理问卷数据和生理数据。对于生理数据，本研究使用Empatica 公司开发的E4 手环，以4Hz 的采样率获取皮肤电数据，以64Hz 的采样率获取心率数据。对于文本数据，研究使用科大讯飞智能录音笔进行会话过程的录制与文本转写，并进行后期人工校对。讨论结束后，主试引导被试填写后测问卷（包含同理心问卷、引领度问卷等）。

三、数据分析

本研究通过多模态数据分析，以期探求设计问题解决过程中的教育新规律与新发现。图1呈现了设计类问题解决能力测评分析的总体工作流程，主要展现了测评过程中不同维度下被试的分布情况，以及各维度所运用的分析方法，直观地将数据分析流程体现出来。其中，数据分析建模部分共用到103 位学习者的数据，而数据融合部分共用到68 位学习者数据，彼此间数据互不相同、互不交叉。

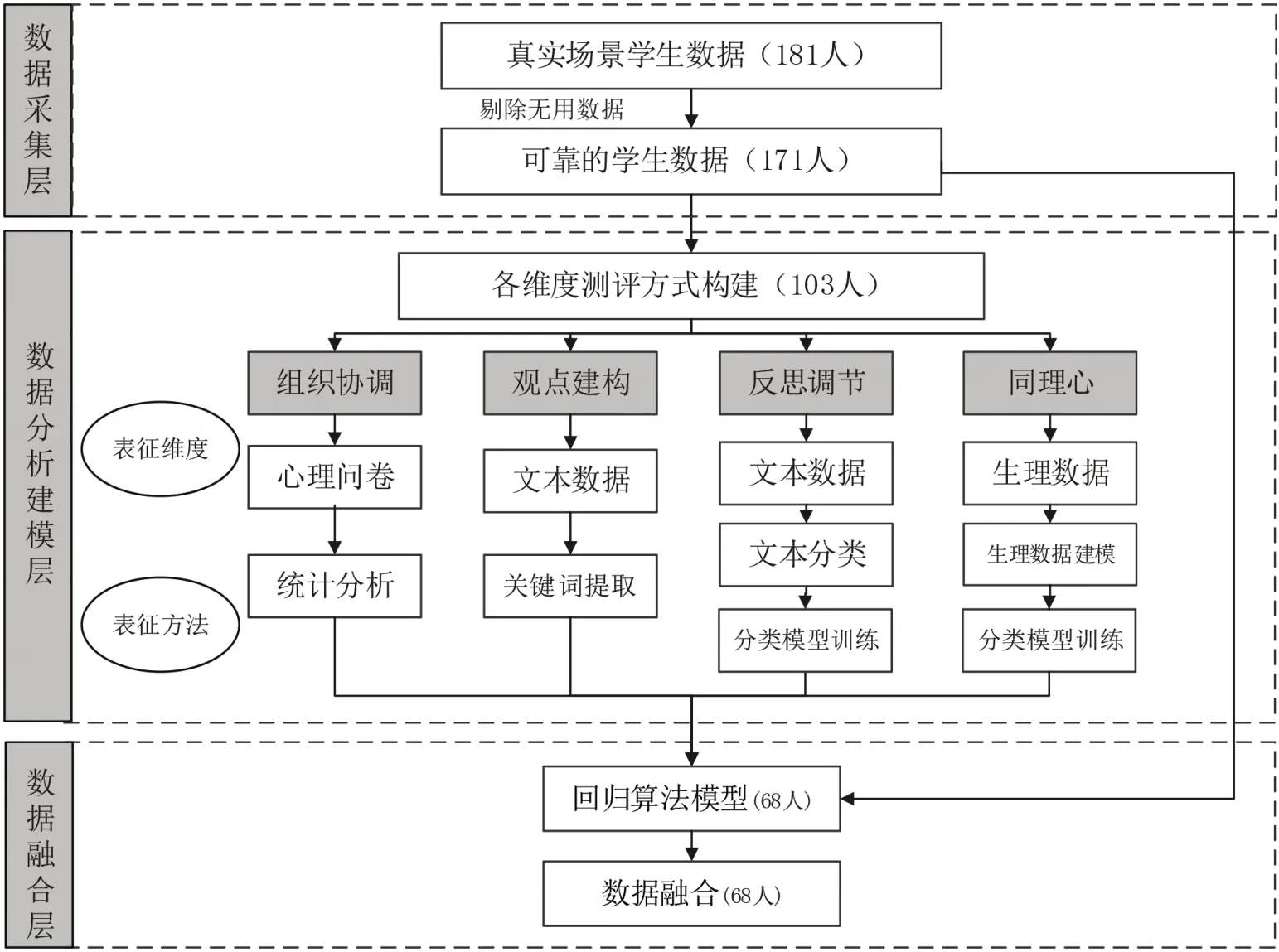
图1 多模态数据表征的设计类问题解决能力表征模型分析路线图

（一）反思调节维度

学习者在协作设计中的言语、行为等可以反映其在解决问题过程中反思与调节的情况，因此，本研究抽取学习者在问题解决过程中动态的、有过程倾向的行为与言语数据，构建基于深度学习的反思调节维度交互文本分类模型，从启发性、构思性、实施性和反思度四种维度对设计类问题解决过程的认知情况进行分析。

1.文本编码

在启发阶段，学习者一般从问题的定义出发，通过小组成员之间的头脑风暴进行灵感的迸发，激活自身信念，为学习做好准备，对任务进行分析从而设定目标和战略规划。在构思阶段，学习者通过自我控制和自我观察，集中精力完成任务并使用有效的策略来实现共同体的目标，主要关注学习者如何综合运用已有的学科知识和问题解决能力进行方案设计。在实施阶段，更加关注学习者如何推动设计进展，使方案更加完善和科学。在反思阶段，学习者通过监控感知到的信息，根据计划阶段设定的目标进行自我评估，并对结果进行归因。本研究设计的反思调节编码框架如表2所示。

表2 反思调节维度数据标注方案

2.文本标注与预处理

本研究采用先人工、后机器的方式预测言语数据所属的类别。在人工阶段，本研究选取两位专家背对背将单独的句子作为分析单元进行编码，每句话分为具有启发性、构思性、实施性、反思度和无关言语五类。当学习者的言语与测评指标中的编码规则重合，则记为1，若发言但没有与编码规则中的句子重合，则记为0，最终将每个指标的频次累计作为该指标的得分。这种编码方式不仅可以避免不同专家之间的差异，还可以更快地处理大量的数据。然后，计算文本数据的Kappa系数，编码一致性系数达到0.85及以上，则证明本研究编码有效，可以进行下一步的自动化编码。

本研究主要从以下四个方面对数据进行预处理：一是删除无效和冗余数据，二是进行文本分词，三是文本向量化，四是数据采样。

3.算法模型训练

本研究选取当前文本分类中较为常见的Bi-LSTM+self-Attention 和BERT 深度学习算法训练文本分类算法模型。

Bi-LSTM在LSTM（Zhou et al.,2016）模型的基础上能够同时考虑前向和后向的时序信息；注意力机制可以更好地处理输入序列中的重要信息。因此Bi-LSTM+Attention模型进一步提升了模型对时间序列数据的处理能力。这种方法在自然语言处理、语音识别、图像处理等领域取得了良好的效果（甄园宜&郑兰琴,2020）。

BERT 通过对大规模文本语料进行预训练，学习总结出通用的文本表征，从而能够在各种自然语言处理任务中进行微调，取得优秀的效果（Devlin et al.,2018）。本研究采用的两种算法模型如图2和图3所示。

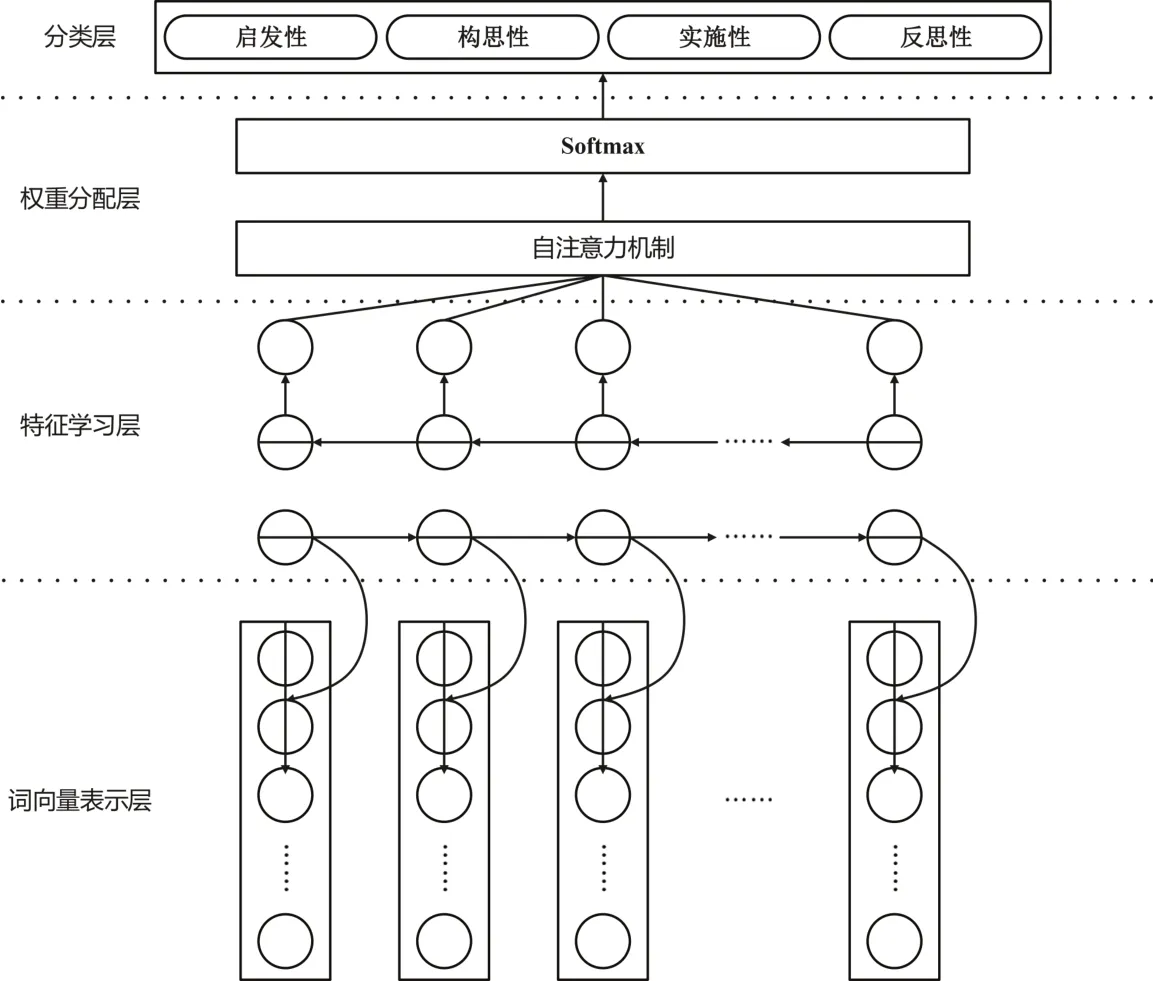
图2 Bi-LSTM+self-Attention算法模型示意图

图3 BERT算法模型示意图

4.文本分类效果

本研究将数据集随机分为80%训练集与20%测试集。利用训练集数据对上述2个文本分类器模型进行训练，获得的分类模型在测试集上进行分类测试的各项指标如表3所示。

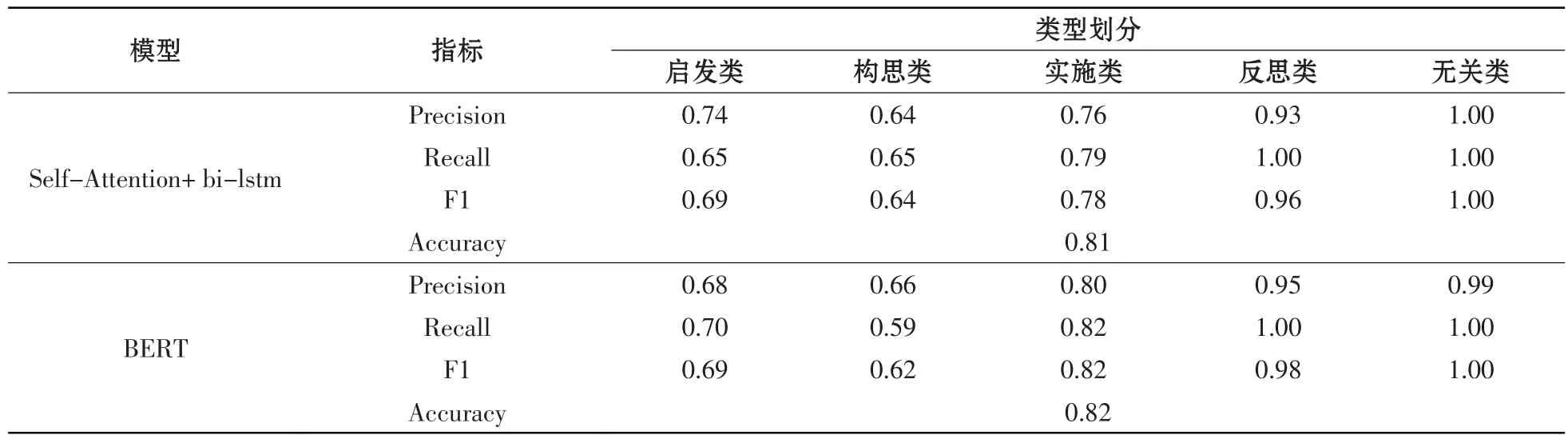
表3 两种深度学习算法在测试集上的分类结果

由表3 可知，BERT 模型的整体准确率较高，表明BERT 模型可以更好地提取实施类、反思类和无关类的语义信息，而在启发类和构思类的语义信息识别上还有待改进。本研究采用BERT模型作为反思调节维度的文本分类最终算法。

5.反思调节维度得分计算方法

BERT 模型在训练集和验证集中的准确率和Loss 值的变化曲线如图4所示。训练轮次设置为20 轮。Loss 值逐渐减小，而准确率逐渐升高，最终验证集上最高的分类准确率达到82%。

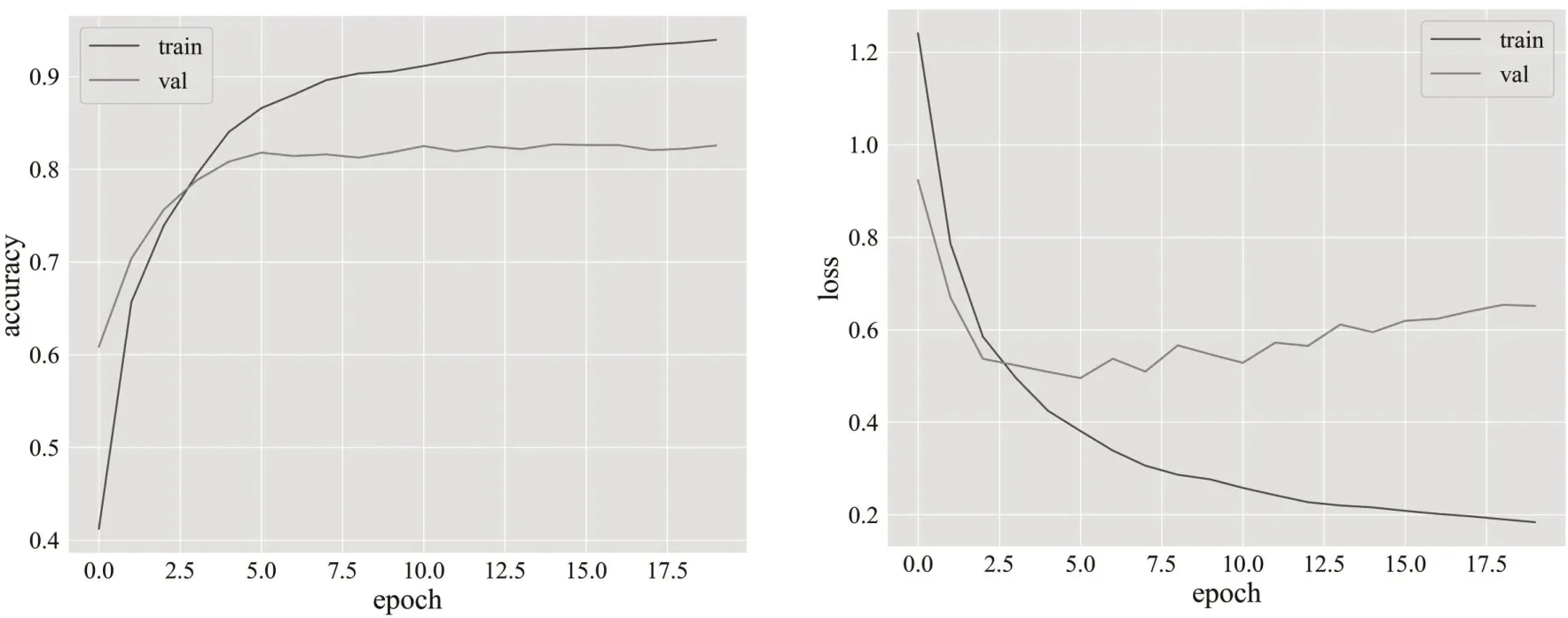
图4 训练集和验证集的准确率和Loss值变化趋势图

图5 为BERT 模型经归一化处理后的混淆矩阵分析结果，其横坐标代表预测标签（Predicted Label），即分类结果，纵坐标代表正确标签（True Label），即实际类型，坐标中的0—4 分别代表启发类、构思类、实施类、反思类和无关信息类5种类型的设计类问题解决能力言语交互文本，矩阵中的数值表示该类交互文本的召回率。从混淆矩阵分析结果可以看出，对角线上的分类预测情况较好，在各个维度上均表现较优，表明BERT分类器具有较好的分类效果。但仅能判断学习者的话语属于哪一个维度还不能完全评判其得分，因此，最终将每个指标的频次累计作为该学生的指标得分，以此实现个体和群体的得分计算。

图5 BERT模型分类混淆矩阵

（二）观点建构维度

虽然知识构建是一种群体现象，但贡献来自可识别的个人。如何度量知识贡献是提高知识构建活动质量的关键。然而，衡量知识建构过程中的贡献在教学实践和研究领域都很困难。信息论提供了一种定量的方法来衡量信息相关系统中信息的内容（Vrankoviet al.，2020）。如果某学习者的交互文本中包含了对此次主题式设计有用的信息，则该学习者就做出了知识贡献，并减少了这个小信息系统产生的不确定性。交互文本信息内容可以通过其中所有关键词的信息之和来衡量。这种方法命名为“知识贡献的信息度量（IMKC） ”（Wu et al.，2021）。在本研究中，采用这种方法探索设计问题可解决学习者观点的科学性、创新性和系统性。本研究构建了基于海绵校园主题的关键词汇总表，共66 个关键词，当学习者交互文本中出现关键词汇时，会进行下一步的计算。观点建构维度下三个量化指标的计算方法如下。

1.科学性

根据香农的信息论，学习者互动文本的总信息量是指文本中所有关键词的信息量之和，通过分析可知，学习者所提出的方案的科学性越好，则说明学习者提出的观点中涉及的知识关键词越准确，因此本研究采用准确关键词的信息总量来表征科学性。其中M 指学习者人数，n 指每个人的句子数，freij指第i 个学习者第j 句话中关键词出现的频率，frek指第k个学习者出现关键词的频率，pk指第k个人所说的话中包含关键词的总概率，见式（1）。

2.创新性

观点的创新性越好，则说明学习者更具创造力，可以提出不同的知识观点，因此采用言语文本的关键词信息增益进行评价。将关于“海绵校园”主题的一个组别的所有文本数据都放置在一个时间轴上。具体算法如下：当学生在讨论中出现与先前不同的新的关键词时，就将该关键词纳入进来。D指上一句话中关键词的个数，R 指下一句话中关键词个数，card|R-D|指新增的关键词个数；ΔI指新增关键词的信息增益。由于每组学生为3人，交互式文本中有对话的情况，因此我们建构了式（3），其中下标i代表第i个学习者，ΔIi为第i个学习者的信息增益，见式（2）和式（3）。

3.系统性

通过分析得知，知识点覆盖度越高，代表学生在合作过程中能更充分地认识到问题涉及的知识面，因此采用关键词的覆盖比例表征学生在讨论中观点的系统性。freij表示第i 个人说到第j 个关键词的词频，N 是关键词总数，uni函数是对词频的记录，sys函数则是对关键词覆盖程度的表征，见式（4）和式（5）。

（三）组织协调维度

组织协调维度主要表征协作过程中学习者之间沟通交流的情况，学习者对小组活动参与越多，投入度越高，则信任感和归属感越高（马志强等,2022），从而有助于小组内部的知识构建和知识分享。合作学习中的协调被定义为“和谐与合作艺术”。协调是为了使一个团体或个人获得预期目标而进行的相互作用。协调包括与团队成员合作，并且针对团队成员建立了一系列彼此相关的计划活动（Malone &Crowston,1994）。有效协调是合作的关键，并依赖于服务与组织间和系统间有效工作关系的建立（Entin&Serfaty,1999）。

由于设计思维维度已经考虑了协作过程中的认知情况，故本节仅考虑协作问题解决过程中学习者交互的情况。本研究采用心理问卷的组间互评与自评来对组织协调维度进行表征。

1.协调度

刘红（2022）在协作能力提升项目的研究中提出了包括协作态度、组织协调和沟通交流的协作能力三维测评框架，并编制了测评量表。其中组织协调包含评价、规则、组织工作、调控四个要素。在此基础上，本研究完善了调控维度的问卷，将其作为协调度的表征问卷，用《协作能力问卷》中的量表来表征学习者在协作设计中组织协调组间关系，维护组间稳定的情况，即协调度。量表共14 题，克隆巴赫系数≥0.7，Bartlett 球形度检验p＜0.01，问卷的信效度较好，可以用于测评。

2.响应度

以往的研究表明，通过参与者与同伴或老师的互动来衡量其参与度是可行的。因此本研究采用《基于项目化学习的协作能力测评》中“协作态度维度”的测评量表对协作过程中的响应度进行测评（刘红,2022,p.22）。问卷包括承担责任、宽容性、协作性和协作意愿四项，共12题，克隆巴赫系数≥0.7，Bartlett球形度检验p＜0.01，问卷的信效度较好，可以用于测评。

3.引领度

本研究采用《青少年领导力问卷（中文版）》对学习者在协作过程中的领导力进行测量（李敏, 2013, pp.95-96）。《领导技能量表（中文版（LSI-C））》是以凯特和汤曾德（Carter & Townscend, 1983）《领导技能量表（修订版）》为蓝本，经过翻译修订和检验的量表，包括团队工作、理解自我、沟通、决策和领导五个分量表，共21 题，克隆巴赫系数为0.91，Bartlett球形度检验p＜0.05，问卷的信效度较好，可以用于测评。

（四）同理心维度

在同理心维度，将构建两个机器学习分类模型，分别为理解力表征的分类模型和体验度表征的分类模型，采用特征工程的方法分别对理解力和体验度进行表征。同理心维度的表征流程图如图6所示。

图6 同理心维度多模态表征流程示意图

首先，本研究对心率、心跳间期、血容量脉冲和皮肤电的数据从频域特征、时域特征、非线性特征等方面进行特征提取（武法提等,2022），共提取170 个特征值。时域特征包括各类信号的标准差、均值、一阶差分最大值和最小值、二阶差分最大值和最小值、四分位距、绝对中位差、偏度、峰度、最大最小值差等；频域特征包括自回归方法、傅里叶方法、Lomb-Scargle周期图法提取的高低频特征（李幼军, 2018, pp.22-27）；非线性包括庞加莱图和去趋势波动分析所提取的特征等（杨敏,2013,pp.15-22）。

其次，以同理心问卷（IRI）的认知共情和情绪共情两个维度的心理测验分数的分类值作为标准得分，分别对理解力和体验度进行机器学习分类算法模型的构建。IRI 问卷是对同理心进行多维评估的经典问卷（Davis,1983），量表共有28 道题，以5 点李克特式计分。随后，对问卷数据进行归一化，将70 分以下设为C 类，70—85 分设为B 类，85—100分设为A类。每位学习者有一组对应的标签和若干组特征值，以此提取有效性高的特征值。在计算特征值后，采用相关分析中的皮尔孙系数对若干特征进行筛选。特征值与体验度、理解力的相关系数的绝对值低于0.3 的特征被删除，其中“理解力模型”和“体验度模型”分别筛选出18 个和23 个重要特征值。

最后，本研究以同理心问卷的认知共情和情绪共情维度水平为验证标签，选用支持向量机、决策树、随机森林、朴素贝叶斯、贝叶斯网络、逻辑回归、K 最近邻七种机器学习算法进行分类模型构建。在验证阶段，本研究选用70%训练集和30%测试集，并将这70%训练集采用十折交叉验证的方法进行分类模型的训练和测试，采用模型的预测准确率（Accuracy）、各类别的平均预测精准率（Precision）与召回率（Recall）以及F1分数（精准率与召回率的调和均值）。

对于同理心的理解力维度和体验度维度的得分预测，随机森林法表现最佳，且预测准确率分别达到了77%和65%，因此，本研究采用随机森林法作为数据分类模型算法，分类效果如表4所示。

表4 理解力与体验度的机器学习分类模型准确率

四、设计类问题解决能力多模态数据的融合分析

多渠道获取的数据主要存在数据类型不同、数据时间难以对齐等问题，如心率、皮肤电的数据为时间序列的连续数据，而行为言语编码的数据为离散数据，这两种数据不能直接进行融合评价。因此将多种来源、通道和场景的数据进行融合是目前多模态学习分析的难点。本研究将前面四个维度所训练得到的问题解决能力各维度模型，通过权重分配融合为一个确定的问题解决能力测量值，以解决该难点。为了保证数据决策模型的有效性和科学性，本研究选取了68 位被试的数据进行数据融合模型的搭建与测试，为了避免数据拟合情况过好，所选取的测试数据与前面模型构建时的数据集完全不同。具体流程如图7所示。

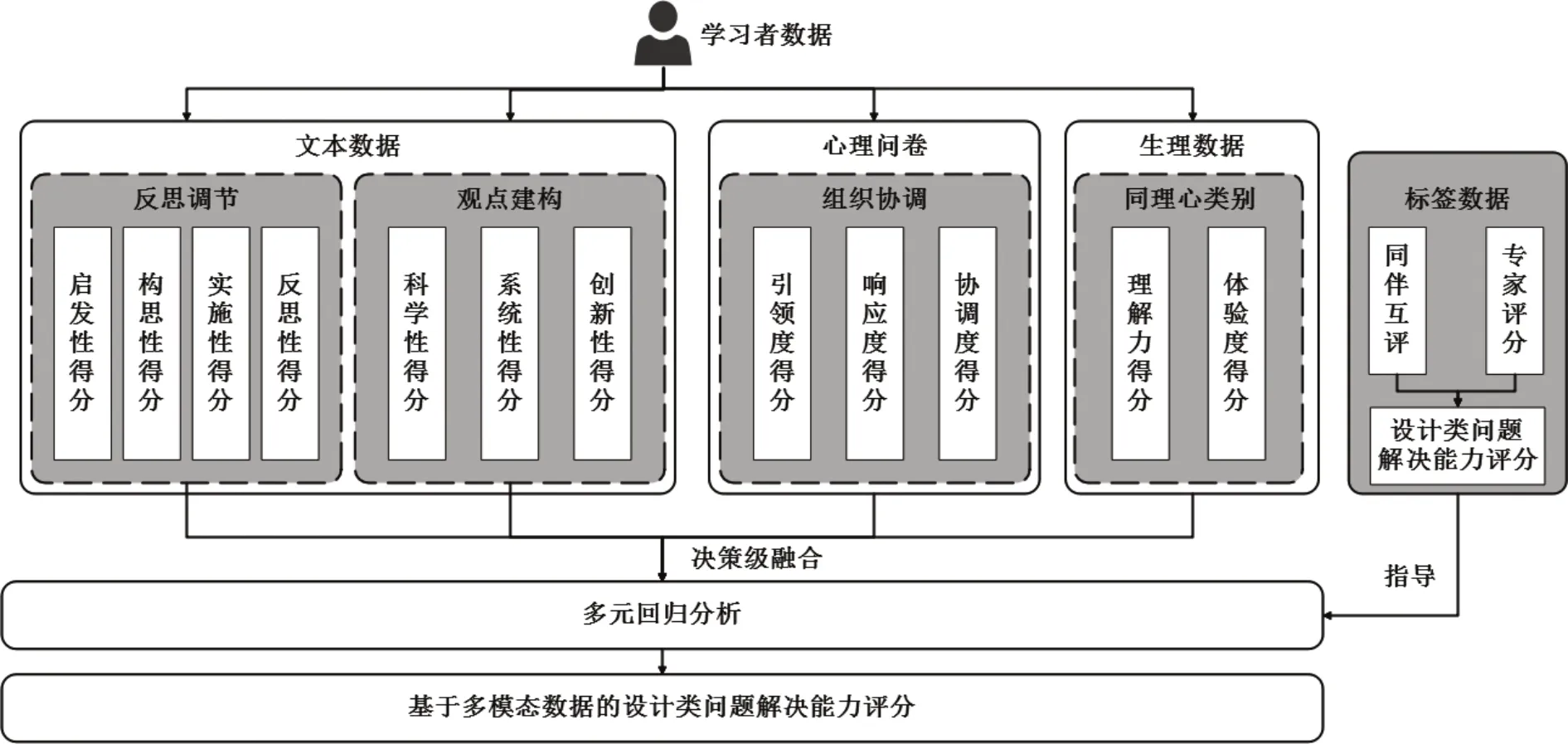
图7 设计类问题解决能力决策级融合流程

融合模型的标签为专家对学生设计类问题解决能力设计方案的主观评分和小组内自评与互评的加权求和。专家的主观评分采用了背对背评分的方式，当两位专家评分之差超过5分时进入第二轮打分，研讨评分原因，并得到最终得分，以保证评分的公平公正，避免由一人评分导致的偶然性。

本研究选取多元线性回归法中的最小二乘法进行数据的预测拟合，探究本研究所提出的四维度的设计类问题解决能力的多模态测评模型是否能够在真正意义上表征学习者在合作过程中的问题解决能力。

首先，需要计算因变量与自变量的关系的正态分布情况和散点图，以此确定因变量与自变量的关系。同时，需要分析残差是否符合正态分布。回归标准化残差在区间（-2, 2）内波动，则说明拟合程度好。自变量和因变量之间呈现线性关系。

其次，多元回归模型分析结果显示，本研究所采用的回归模型R2=0.725，说明可以解释72%的因变量变异。

接下来对模型的显著性进行检验，方差为F=59.509（p＜0.05），说明模型显著，拒绝回归系数为0 的原假设，因此模型基本满足要求。通过多元回归模型，我们得知，该模型可以运用多模态数据表征设计类问题解决能力。

在明确模型能够表征设计类问题解决能力后，需要明确每个要素的权重，以便了解影响问题解决能力的具体要素及其比重。从标准化系数来看，在统计学中将设计类问题解决能力的回归方程为：设计类问题解决能力得分=-0.223×构思性+0.165×启发性-0.127×实施性+0.144×反思度+0.225×领导力+0.097×协调性+0.221×响应度+0.118×系统性+0.194×科学性+0.227×创新性+0.234×识别度+0.167×体验度。

标准化回归方程可以解释不同变量间的影响程度。标准化系数越大则变量对因变量的影响越大。由回归方程可知，同理心维度和反思的程度对设计类问题解决能力的影响比较大，因此学习者需要加强在问题解决过程中对同伴的理解与共情以及不断地反思与迭代的能力。图8展示了本次模型的原始数据图、模型拟合值、模型预测值。由图8 可知，模型拟合情况较好。

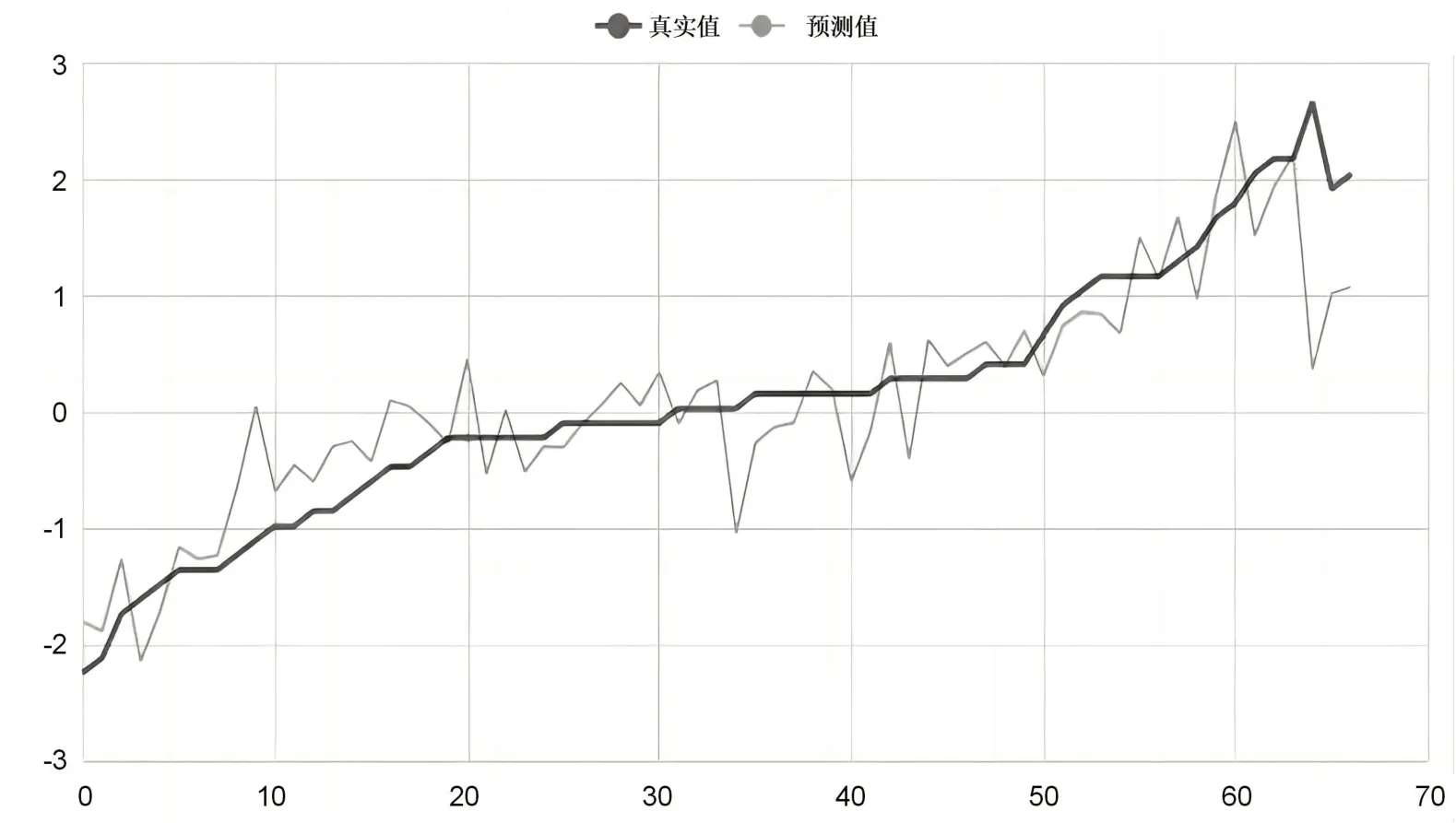
图8 回归模型的拟合效果图

至此，基于多模态数据的设计类问题解决能力表征完成。

五、讨论

设计问题具有复杂性、社会性等特性。设计类问题解决能力涉及多个维度，从学习者的内隐心理和外显行为，到社会文化情境中身份、存在感和社会关系等。本研究以多模态数据设计类问题解决能力的测评为主题，拓宽了问题解决等高阶思维的测评范式，也为精准化能力提升与干预的发展带来重要转机。

（一）精准的数据采集和特征提取是基于多模态数据的设计类问题解决能力测评的基础

首先，本研究基于已有的测评框架开展了设计类问题解决能力的测评实验，招募了181位被试，并收集了其在讨论过程中的文本、生理和心理问卷的过程性数据。通过从过程的视角进行测评，可以更全面地了解学生在设计类问题解决过程中的思考和表现。这为教育者提供了一个深入了解学生学习过程的机会，从而更好地调整教学策略和课程内容，以促进学生的设计能力和问题解决能力的发展。其次，研究采用BERT算法、随机森林算法和关键词词频分析法等数据挖掘方法对数据进行了分析。这表明设计类问题解决能力是一种可测的能力，教育者可以借助机器学习和数据分析的工具和方法，提供精细化的测评和个性化的反馈。这有助于教育者更好地了解学生的学习情况，为他们提供更具针对性和更有效果的教育支持。因此，本研究基于多模态设计类问题解决能力测评实证，总结出基于多模态测评设计类问题解决能力精准测评的基础——数据获取与特征提取。每个环节都需要用感知技术、识别技术和融合技术等关键技术来提取和处理多模态交互信息，以实现对参与者行为、社交和认知等方面变化的聚合判断。与现有研究中单一和静态的分析方法相比，这种方法弥补了这一缺陷。

（二）多模态融合有助于设计类问题解决能力表征的准确性和可解释性

深度学习技术因其以数据驱动学习的特点，在自然语言处理、图像处理、语音识别等领域取得了巨大成就（任泽裕 等, 2021）。但将大量的多模态数据进行整合分析存在较多困难，且费时费力。因此，多模态数据融合分析既是多模态学习分析的核心，也是难点。本研究通过各类算法将学习者各维度得分计算后进行决策级融合，采用回归分析的方法，确定不同维度的权重分配。首先，采用算法和数据分析的手段，更全面地了解学习者在各个维度上的表现，这有助于教育工作者更准确地评估学生的学习情况，并对其进行有针对性的指导。如通过算法分析，我们可以发现学生在某一维度上表现不佳，从而帮助教育者识别并解决学生的学习障碍。其次，通过决策级融合的方法将不同维度的得分综合起来，可以得出一个更准确和更综合的评估结果，这有助于消除单一维度评估的片面性，更全面地了解学生的学习能力和水平。通过分析和融合多个维度的数据，教育者可以更好地了解学生的优势和不足，以制定更有针对性的教学计划。此外，决策级融合方法的数据均来自不同的数据分类器或模态结果，每个模态的数据之间互不影响，可单独计算，错误不会累计，这也提升了分析模型的准确性和容错率。通过合理地分配权重，教育者可以更好地理解学生在各个维度上的重要性，从而在制定教学计划和课程安排时更加科学和有效，更好地满足学生的学习需求，提升整体教育质量。

采用合理有效的多模态融合方法可以充分利用多模态信息之间的互补性，获得更完整、更好的特征表达，从而在保证模型效果的情况下，在学习的过程中针对不同的特征实现不同程度的强化，这对深度学习的可解释性有一定的帮助，也为深入表征设计类问题解决能力提供了清晰的方法体系。

（三）问题情境创设是设计类问题解决能力测评的前提

在设计类问题解决能力的测评中，问题情境创设至关重要。由于设计问题是一种复杂、开放的问题，设计类问题解决能力测评情境的创设需要考虑学习者在设计过程中综合利用其他资源和相关知识，并运用各类工具动手实践的水平。因此，设计问题解决能力的测评需要为学生提供一个有效的问题思考情境，这种情境使得测评不仅仅是对学生知识的考核，更是对他们理解、应用、分析、评估和创造知识能力的综合评价。问题情境应模拟现实生活中的复杂问题，如环境保护、城市规划、可持续发展等。本研究以海绵校园为情境进行设计问题解决测评，涵盖了地理、物理、化学等多个学科领域的知识。这种综合学科的情境设计有助于打破学科之间的界限，促进跨学科思维和学科知识的综合运用。

研究表明，仅关注整体的设计思维和协作水平是不够的，还需要多维度、分层次对学习者的设计过程进行表征和干预。在设计类问题解决活动中，教学者应注重培养学生的启发思维、反思能力、领导力、应变能力、系统思考能力、科学探究能力、创新意识和问题识别能力，从而综合提升他们的设计类问题解决能力，有助于提升他们的创新能力和适应未来挑战的能力。

六、总结

未来的研究中，设计类问题解决能力的培养和测评应聚焦于几个关键领域。首先，提升数据采集的精准性和降低入倾性是基本出发点，要确保获得的信息准确反映学生的实际表现和能力。随着数据量的增长和复杂性的提高，自动化数据预处理工具的研发将成为重要的研究方向，旨在减轻处理大量多模态数据的负担。其次，不断迭代和优化测评模型，提高其信效度，以应对学生表现的偶然性和多样性，是确保评估结果准确性和有效性的关键。这种测评不仅关注学生的设计思维和创新能力，还将评估他们的批判性思维、问题识别、团队协作和领导力等高阶能力。此外，随着计算技术的进步，大规模计算机辅助测评将成为可能，不仅能提高评估效率，还能为每个学生提供个性化的反馈和指导。总体来看，未来的设计类问题解决能力测评将更加精准、高效和全面，更好地促进学生在复杂多变的世界中发展创新能力和高阶思维能力。基于多模态数据的智能化测评是一种新兴的研究方式，需要研究者通过不断的改良和优化推动其发展。