粘粒级配对黄土动力特性影响的微观机理分析

赵宁 ZHAO Ning

（中铁第五勘察设计院集团有限公司，北京 102600）

0 引言

黄土作为一种多孔隙、弱胶结的沉积物，其物质组成、颗粒形态十分复杂[1]，与许多宏观力学特性紧密相连的是粒级配比和微观结构变化。在承受动力荷载的工程实践中，黄土的颗粒级匹配变化对动力特性的影响十分明显。我国黄土粒级分布，其特点是由西北向东南逐渐增大，在空间上呈粘粒状变化。因此，对黄土因粒级变化而产生的物理力学性质和差异，以及对其微观机理的探究，都有必要进行系统的研究。

在动力荷载作用下土体表现为弹性、塑性和粘滞性的粘弹性体[2]，而黄土由于其独特的动力性质，在地震中常常会引发液化等地质灾害[1]，具有较强的地震易损性。自D’Appolonia 首次在分析液化问题时考虑了粉粒和粘粒不同配比对动强度的影响[3][4]，国内外学者开始对粘粒与土动力特性间的内在联系做了广泛的研究，且已经取得了不错的研究成果。随着研究的深入，李兰等对不同粘粒含量的原状甘肃黄土、曹成林等对不同粘粒含量的黄河三角洲粉质土、孟凡丽等对不同粘粒含量的杭州饱和粉土行进动三轴试验都得出了相似的结论，不同的粘粒级配对试样动强度的影响显著，且呈非单调关系。王勇等它的内在机理是从微观结构上进行探讨的。从前面的上述研究可以看出，对于影响土体动力特性的重要因素——粘粒，人们已经普遍认同，但大多数研究的重点还是在动力强度上。目前，有关动模量与阻尼比的相关研究主要是对不同区域黄土的统计比较，特别是对黄土粘粒级成对动模量与阻尼比作用机理的探究研究还比较少。

近年来，我国在黄土地区规划、新建及改建的铁路工程愈加增多，列车在运行过程中动荷载对黄土地区地层的影响成为了愈加关注的课题，土的动剪切模量和阻尼比作为描述土动力特性的两个基本参数，已经成为了土层地震反应分析和场地地震安全性评价中的必备指标。通过对黄土动力特性参数在不同粘粒含量条件下的测试结果进行综合分析，得出总体规律：对粘粒级配之于黄土动力特性的影响机理，我们利用黄土二元结构微观概念模型进行分析和探讨。本文通过对黄土地区铁路工程在动力荷载环境下的黄土级配影响机制的讨论，对其微观结构对动力特性的影响机制进行分析，并对黄土地区铁路工程进行理论指导。

1 试验方案

本次试验采用的土样取自某铁路工程钻孔岩芯中地表以下6m 的黄土地层，基本物理参数见表1。土样先后经过0.5mm 和0.05mm 的干筛去除散砂粒，再利用激光粒度仪对土样粘粒含量进行跟踪测量。由于原始黄土除去砂粒后所得到的粘粒含量通常在25%以下，我们在实验中准备了四种扰动黄土土样进行测试，它们的粘粒含量分别为12%、16%、20%和24%。土样级配方案如表2 所示。

表1 土样的基本物理参数

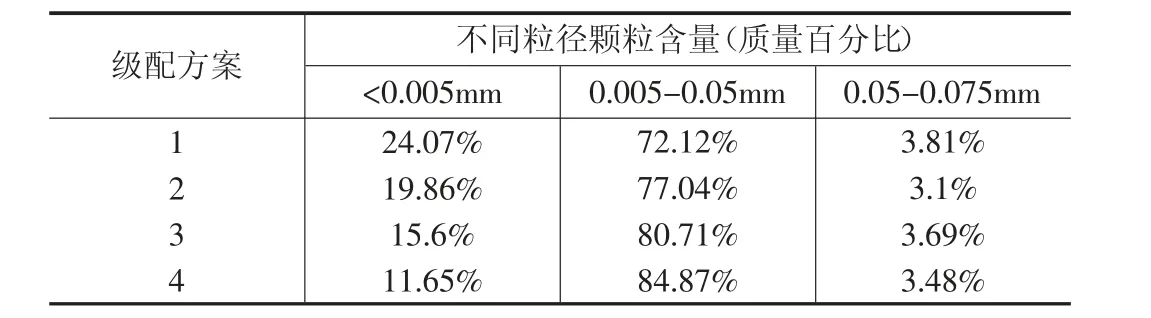
表2 试样级配方案

将筛选好的黄土样本混合适量的水，静置其中，使其水分含量达到自然状态。土样是根据《铁路工程土工试验规程》（TB10102-2010）的规定，采用干密度1.5 克/立方厘米，配成φ39.1×80mm 的圆柱形试样。试样在真空饱和器中抽真空饱和器，采用冷冻法将试样装入试样中。在200kPa 压力条件下进行长达1 小时的饱和试样等压固结，并在固结完成后进行固结不排水动三轴试验，频率为1Hz 正弦波振动。

2 试验结果分析

2.1 动剪切模量 根据图1 试验结果，对黄土试样的动剪切模量和动剪切应变的关系曲线，分别用不同粘粒含量表示。黄土试样中粘粒含量不同的动剪切模量随动剪应变的增加而逐渐减少，表现出刚度软化现象；在相同动剪应变条件下，粘粒含量对动剪切模量的影响表现为非单调变化，随着粘粒含量的增长，黄土试样的动剪切模量呈现先减小后增大的变化趋势，本次试验在粘粒含量为16%～24%时达到临界值。

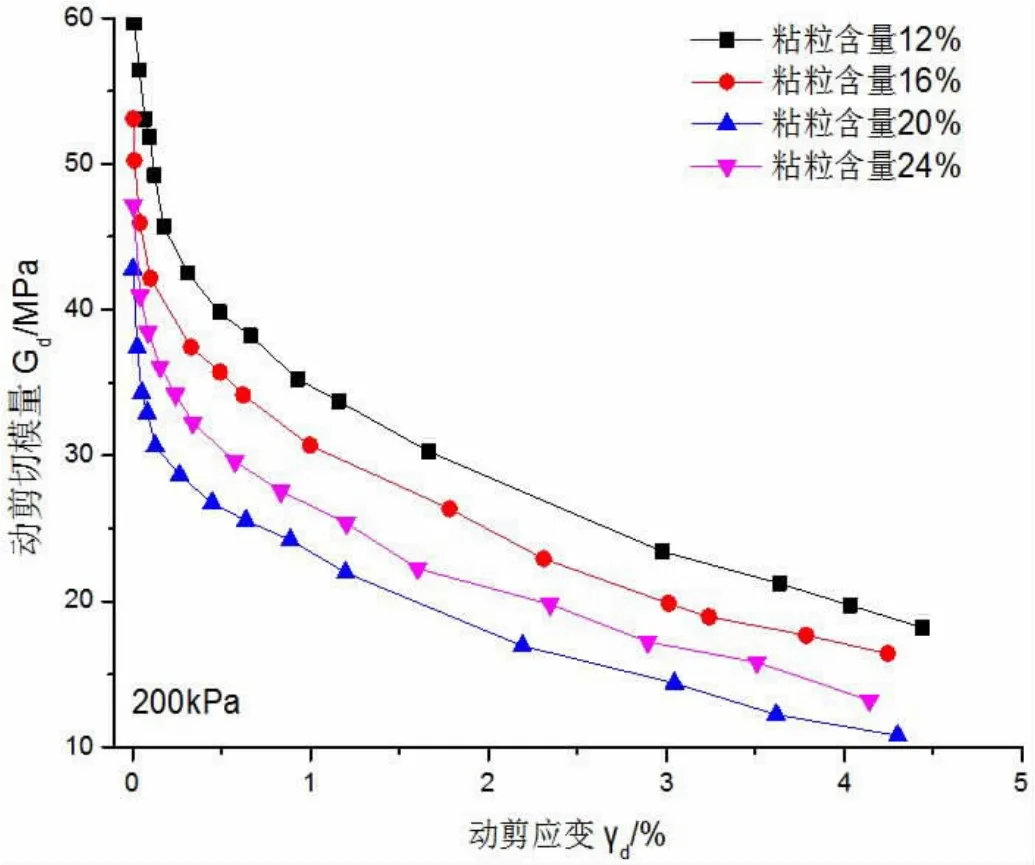
图1 不同粘粒含量条件下Gd-γd 关系曲线

由图1 观察可得，在动剪切应变关系曲线中，不同粘粒含量的黄土试样表现出类似的发展模式，它们都表现出双曲线的良好特点。这符合哈丁双曲线模型对土动应力应变关系的变化趋势，即公式（1）所示。根据哈丁双曲线模型，动剪切模量倒数与动剪应变拟合结果呈线性关系，如公式（2）所示。

式中：a、b 为土的试验参数。

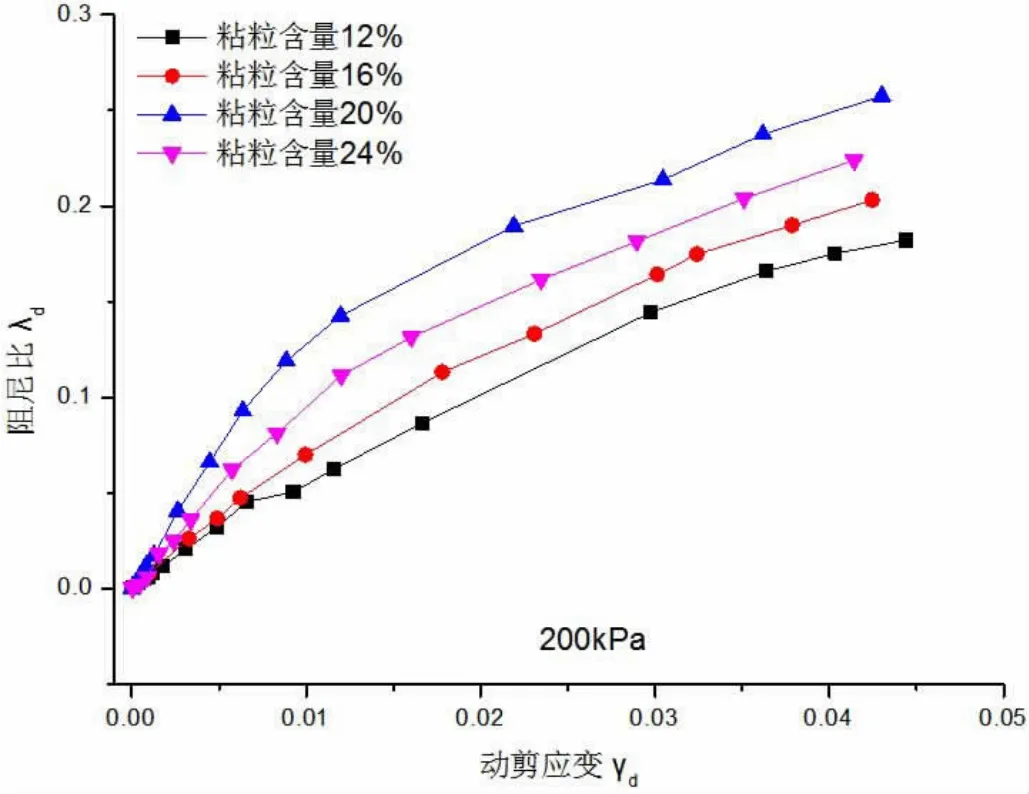
图2 不同粘粒含量条件下λd-γd 关系曲线

表3 不同粘粒含量条件下参数a 取值

结合表3 观察参数a 与Gmax的关系可以看出，在粘粒含量增加的情况下，参数a 呈现出变化趋势，先增后减，初始动剪切模量（最大）呈先减后增的趋势，粘粒含量临界值在达到最小值时，由于粘粒含量变化引起的粘粒赋存位置的改变，黄土试样的初始动力特性受到了显著的影响。

2.2 阻尼比 通过试验数据可得，图2 显示了重塑黄土试样的阻尼比与动剪应变的关系曲线，从图中的资料可以观察到，粘粒黄土样含量不同，其阻尼比随着动剪应变的增加而逐渐升高。在小应变时，阻尼比变化幅度相对较小，然而，当动剪应变变得更大时，直到最终稳定下来，阻尼比的增长速度才明显加快。粘粒含量对阻尼比的影响在相同的剪切应变条件下是不单调的。黄土试样的阻尼比会随着粘粒含量的增加而出现先升高后减小的现象。当粘粒含量为16%～24%时达到临界值，并且该趋势在高剪应变水平时表现更加明显。这一结果表明，在黄土试样中，对动荷载响应的滞后效应随着粘粒含量的不断提高，呈现出先增强后逐步减弱的变化特点。

由于哈丁双曲线模型对阻尼比拟合效果不佳，因此在实际应用中，多采用幂函数经验，即公式（3）所示。

公式中：λmax为最大阻尼比；β 为阻尼比曲线的形状系数，是与土性质有关的拟合参数；Gmax为最大动弹性模量。

根据公式（3）可得到拟合曲线回归参数最大阻尼比λmax与曲线形状系数β，根据表4 中的统计结果绘制总结可得：阻尼比是体现土体对动荷载响应的重要指标，λmax则是等效动粘弹性本构模型的重要参数，总结观察λmax的变化规律，对分析不同粘粒含量黄土试样等效动粘弹性本构模型参数间的差异起到决定性的作用。

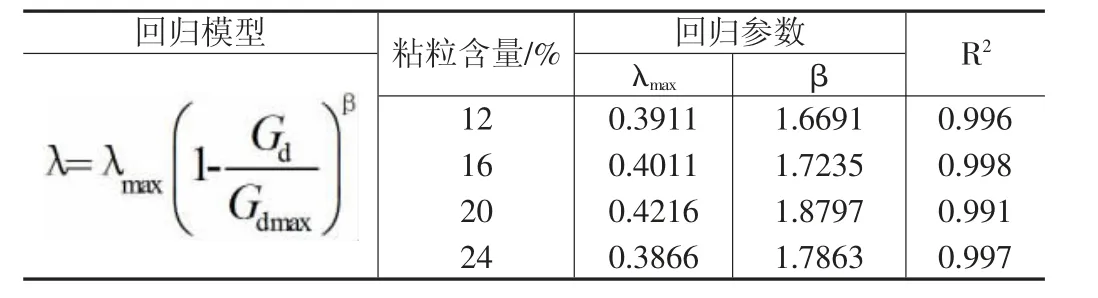
表4 幂函数经验公式回归曲线参数

通过表4 数据可知，粘粒含量的增加会导致阻尼最大值的比值，在粘粒含量增加到临界值时，粘粒含量会先增大后减小，达到最大值。这种变化趋势符合阻尼比的变动规律。再次证明了粘粒含量的变化对于黄土动荷载响应的滞后性是有影响的。

3 粘粒级配对黄土动力特性影响机理分析

3.1 不同粘粒级配黄土微观结构特征

通过分析黄土试样具有不同粘粒级配的微观特性，了解动剪切模量的大小及粘粒对黄土阻尼比的作用机理。以粘粒为主要成分的粘土矿物集合体，其微观结构是极其复杂且形态各异的，它通常存在于粒径较大的粉粒颗粒周围或以集粒状态聚集在大孔隙内。黄土颗粒或集粒间胶结、挤压、镶嵌等接触方式称为“力链”，这些力链之间的相互作用程度不同，造成了黄土在宏观力学特性上的不同表现。黄土是由一定比例的粉粒、粘粒混合而成的泥沙。在观察样本微观结构时，可将其分为两个阶段，黄土试样的二元结构概念模型，如图3 所示，表明粘粒含量的不同，其变化的大小不同。

图3 不同粘粒含量黄土二元微观结构概念模型

试样的土骨架在第一阶段是由接触到的粉粒（particle）组成。粒径较大的粉粒颗粒主要影响宏观力学性质，而粘粒则起到传导性辅助作用。通过图3（a）-图3（c）可以说明这种情况。在图示结构中（图3（a）），与以粉粒为主的力链相互作用较少的粉粒骨架形成的孔隙中，主要分布粘粒。在图3（b）中的结构中，孔隙中存在粘粒的一部分，粉粒与粉粒之间的接触点存在着一部分，并将粉粒与粉粒逐渐分开，从而参与到骨架的形成过程中。在此过程中，粉砂链中的相互作用会因粘粒的作用而减弱，从而使外荷载的传导速度变慢；在图3（c）所示结构中，由于聚合态的粘粒较少，导致以粘粒为主导的力链之间的相互作用仍然较弱，因此，粉粒颗粒被粘粒完全分离。这就意味着，粘粒集粒还没有担当起黄土骨架的角色。此阶段以粉粒为主导的力链间相互作用最小化，由此进入第二阶段的微观结构（microstructure）。

土体骨架在第二阶段是由粘粒聚集而成，主要由粘粒性质决定试样的宏观力学性质，而粉粒起辅助作用，如图3（c）-图3（d）。从图3（c）所示的状态来看，以粘粒为主导的力链的相互作用逐渐加强，以粘粒数量的增加、集粒数量的增加和相互接触而导致集粒开始承担土体的骨架作用。当粘粒增大到图3（d）阶段时，粉粒被粘粒包围，近似于“悬浮”状态。以粉粒为主的力链之间的相互作用，在土体中已经不存在了。聚合粒之间的排列随着粘粒含量的增加而变得更加紧密，从而引起了更快的外荷载传导速度。

由上述分析可以得出，随着粘粒含量的增长，在试样整体孔隙比不变的情况下，应存在某一临界粘粒含量值，由粉粒控制黄土的宏观力学性质向粘粒控制黄土的宏观力学性质转变，呈现出前后临界值相反的力学变化趋势。不同粘粒含量黄土试样的动剪切模量变化规律及阻尼比变化规律可根据该临界含量进行分析，粒间孔隙比可引入其中。

3.2 基于粒间孔隙比的粘粒影响机制分析

当粘粒含量超过一定阈值时，会因粘粒的存在而使粉粒间的接触点减少，从而使粉粒间的接触点发生隔断。进而使得土体内部受粘粒控制的力链相互作用，导致土体宏观力学性质受到影响。以粘粒间力链相互作用为主导力量，随着粘粒数量的增加而逐渐增强。在相同剪应变水平下抵抗变形的能力随之加强，导致动剪切模量增加；同样，应力波在土中的传播速率相比粉粒颗粒被隔开过程变快，使土样对动荷载响应的滞后性减弱，阻尼比随之降低。此时以粘粒级颗粒构成的集合体相互接触共同承担土体骨架作用，其粘粒间孔隙比ec可通过公式（4）得到：

式中：e 为土体总孔隙比；Qc为粘粒含量（质量百分比）。

根据式（4）推论，当粘粒含量超过临界值时，粘粒会完全隔离粉粒颗粒，并将颗粒间的空隙逐渐填满，形成包裹层（package）。此阶段粉粒不再扮演骨骼粒子的角色，主要由其粘粒性质决定黄土的动力特性。随着粘粒含量的增长，粘粒孔隙比ec逐渐减小，如图4 所示，集粒间接触点随之增加，相比小于临界含量时粉粒颗粒的分离过程，动剪切模量与阻尼比均出现与其相反的变化趋势。

图4 粘粒含量与粘粒间孔隙比关系曲线

4 结论

本文通过对不同粘粒含量黄土试样进行固结不排水动三轴试验，获得动力学参数，分析动力学参数随粘粒含量增长的变化规律，并利用二元结构微观概念模型讨论了粘粒级配对黄土动模量、阻尼比的作用机理，可以得到以下结论：①粘粒含量对黄土动剪切模量的影响在剪切应变条件相同的情况下是不单调的。动剪切模具的量会随着粘粒含量的增加而先减少，再逐步增加。在临界含量时达到最小值。②粘粒含量对黄土阻尼比的影响在同等剪应变条件下也是非单调的。阻尼比随粘粒含量的提高而呈先增后减的态势。临界含量达到了，就达到了极值。③当黄土试样的总孔隙比保持不变时，在此临界值的前后，使黄土的宏观力学特性呈现出相反的变化趋势，这时粘粒含量随粘粒含量的增加，应该有一个临界的粘粒含量值。④黄土微观特征能很好地说明黄土动剪切模量和阻尼比的影响机理，并通过粒间孔隙比的引入进行量化分析。