分布式接收宽带多目标信号盲检测迭代处理方法
张 凯,刘 义,李运宏,潘冠宇
(63891部队,河南 洛阳 471003)
0 引言
随着电子器件的小型化和集成度持续提升,基于多传感器分布式接收的信号检测技术[1-4]受到广泛关注,其能够有效抑制环境噪声和信道衰落效应的影响,提升信号检测的有效性和鲁棒性,在军用、民用等众多领域具有重要的应用需求和研究价值。
传统信号检测方法主要包括能量检测[5-6]、最大特征值检测[7]、匹配滤波检测[8]、循环平稳检测[9]等。针对多传感器分布式接收的具体应用,文献[10]研究了协作频谱感知的门限选取策略。文献[11-12]分别提出了利用多通道接收信号协方差矩阵和多通道接收信号波形作为网络输入的深度神经网络(Deep Neural Network,DNN)检测方法。随着软硬件技术的飞速发展和宽带接收机的广泛使用,频谱检测向着高瞬时带宽的方向发展,接收频带通常包含多个目标信号,且信号数量及频谱位置可能未知。传统方法主要基于信道化处理策略[13],将接收频段划分为若干子带,使用单信号检测方法依次完成各子带内信号存在性的判别,搜索速度慢,处理效率低。对此,文献[14]提出了基于噪声估计的宽带频谱感知算法,在噪声功率估计基础上,通过对各频点功率测量实现多信号检测。文献[15]则在已知目标信号数目上限条件下,研究了基于稀疏约束最小均方(Least Mean Squares, LMS)的宽带信号检测方法。文献[16]提出了基于卷积神经网络(Convolutional Neural Network,CNN)的频谱感知方法,能够实现多个LTE和WiFi信号的快速检测识别,但需要利用大量先验已知信号样本进行训练。在多传感器分布式接收场景下,由于接收信号信噪比较低、可用数据较短、先验信息(包括信号波形、频谱位置、信号数目等)缺失等不利因素的影响,设计鲁棒高效的检测算法,对来自多个传感器信号进行有效融合,实现宽频带多目标信号的高效一体化检测,一直以来都是研究的重点和难点。文献[17]提出了基于压缩感知的授权用户的位置、个数以及功率传播图估计和定位方法。文献[18]则提出了基于软信息合并的写作频谱感知方法,提升频谱检测性能。
本文提出了基于变分贝叶斯的分布式接收宽频带多目标信号盲检测迭代处理方法。所提方法特色及创新之处主要体现在2 个方面:一是在对信号特性分析的基础上,通过构造线性模型,在贝叶斯估计模型下,分析了各未知参数变分分布解析表达式,通过多传感器信号、多参数的联合估计,有效提升了短数据下的算法处理效能;二是理论推导了信号检测门限解析表达式,实现了特定虚警概率下未知多目标信号盲检测,提升了算法灵活性和稳健性。
1 系统模型及问题描述
考虑典型的多传感器分布式接收系统模型,采用L个传感器进行分布式接收,离散接收信号可表示为:
式(1)中:K为接收频段内的信号数目;sl,k(n)=al,k(n)exp( j2πnfkTs)为第k个目标信号在接收单元l处的分量,Ts为采样间隔,al,k(n)和fk分别为对应信号复包络和载波频率,不同信号频率不重叠;为零均值加性复高斯白噪声,同一支路噪声的实部和虚部以及不同路噪声间均相互独立。在窄带信号模型下,可认为信号包络al,k(n)在一定观测时间内近似保持不变,从而式(1)模型可简化为:
式(2)中,Al,k为al,k(n)在对应观测时间段内的值。
令B为接收频带宽度,以γ=B(M-1)为间隔,对接收频段进行均匀划分可以得到离散频率集合为,其中,φ1和φM分别对应接收频段上、下边界。进一步,将观测时间0 ~T内离散信号序列xl(n) 均匀划分为P段,每段信号长度为N,即T=NPTs,则式(2)可表示为如下多维观测矢量(Multiple Measurement Vector,MMV)的形式:

2 基于变分贝叶斯迭代的检测方法
2.1 多参数联合估计
令θ表示所有未知参数的集合,基于式(3)信号模型,在给定观测信号样本X={X1,X2,…,XL}条件下,变分贝叶斯通过构造简单可解的变分分布q(θ)来替代真实的后验分布p(θ|X)对θ进行近似估计,近似误差用Kullback-Leibler (KL)散度来度量,如下式:
X为已知观测量,lnp(X)为固定值,因此,为使式中KL散度最小,只需对ℒ(q(θ)) 最大化即可。借助平均场理论对未知参数进行分解基础上,变分贝叶斯采用迭代处理方式对各参数变分分布进行联合求解[19],迭代估计式为:
式(5)中:θk∈θ为θ的子集;θ-θk为θ中去除θk以外元素的集合;C为归一化因子。由贝叶斯准则可知,式(5)右边积分项中联合概率分布p(X,θ)=p(X|θ)p(θ)为似然函数和先验分布的乘积,其中,p(X|θ) 为多维复高斯分布。

基于上述先验假设,将p(X|θ)和p(|α)带入式(5),即可求得hp
l变分分布为高斯分布:
同理可得,γm=的变分分布为Gamma分布:

从而可得αm变分后验均值为:
可以看出,αm的估计使用L路接收信号进行联合估计,相比于传统使用单路信号的估计策略能够获得更优的估计精度。同理,噪声精度参数βl=变分分布也为Gamma分布,即:
上述求解为迭代处理过程,算法依次完成未知信道参数和超参数的估计。在迭代的过程中,很多超参数αm取值趋近于0,传统稀疏求解方法[20-21]采用固定门限的方式,当αm值小于某一预设固定门限时,将对应元素值强制置为0,门限的选取与系统性能紧密相关。下一节将结合信号检测的实际,给出新的门限选取策略。在每次迭代参数估计基础上,利用接收信号及信道参数的统计量对检测门限进行更新,能够实现特定虚警概率下的多信号检测,以提升算法灵活性和稳健性。
2.2 信号检测门限推导
基于上文的分析,与频率集φ对应的任意一个频率网格φm±γ2,m=1,2,…,M,信号检测可归结为如下二元假设检验问题:
式(14)中:ℋ0表示与φm对应的频率网格没有信号;ℋ1表示该网格有信号存在。为衡量ℋ0和ℋ1这2 种假设的关系,定义如下对数似然函数:
式(15)中:H={H1,H2,…,HL}和Z={Z1,Z2,…,ZL}分别为式(3)信号模型中未知信道系数和加性噪声的集合,β={β1,β2,…,βL}。
显然,ℋ0和ℋ1这2 种假设下,该似然函数的差异仅体现在等式右边第1 项,即ℋ0假设下,删除了与αm相关项,从而忽略与观测信号样本无关项。利用变分贝叶斯每次迭代获得的参数估计值α和β、ℋ0和ℋ1这2种假设的对数似然比可表示为:

量,可作为检验统计量,即:

基于上述统计量,当Z0(X)小于某一门限值λ时,可判ℋ0为真,即与φm对应的第m个频率网格没有信号,对应虚警概率为:
反之,在给定的预设虚警概率下,可求得对应信号检测门限值为:
实际处理中,通过预设虚警概率,先利用式(20)计算得到信号检测门限,在变分贝叶斯迭代过程中,利用每次迭代求得的参数估计结果,基于式(17)即可计算检验统计量Z0(X)。当Z0(X)<λ时,判定ℋ0为真,即φm对应频率网格没有信号存在,将αm强制置为0,可实现特定预设虚警概率下的未知多目标信号的盲检测,后面通过仿真对此进行验证。
2.3 算法流程及复杂度分析
上述分布式接收多目标信号检测算法采用多组参数变分分布软信息交替计算的迭代处理方式进行联合求解,每次迭代,利用新求得的参数估计结果计算检测门限值,将低于检测门限的相关参数置0,同时删除字典矩阵Φ中对应的列矢量,具体流程如下。
步 骤1 初 始 化:令ρm=δm=al=cl=10-10、j=0、βl=1、αm=1/M;设定虚警概率Pfa,并计算检测门限
步骤2 分别利用式(8)(9)计算的变分后验均值和变分后验协方差矩阵。
步骤3 利用式(11)计算αm变分后验均值αˉm。
步骤4 利用式(12)计算βl的变分后验均值βˉl。
步骤5 对于m=1,2,…,M,若则令αm=0,同时删除Φ中对应的列矢量。
步骤6 令j=j+1。
步骤7 若前后2 次关于α的估计值误差小于10-6或迭代次数大于20,则结束迭代;否则,重复步骤2~6。
步骤8 利用算法收敛后的α估计结果中非零元素的判定,即可实现未知多目标信号的检测。
从上面流程可以看出,所提信号检测方法主干为基于变分贝叶斯软信息迭代的多参数联合估计,在每次迭代基础上,利用虚警概率预设值计算信号检测门限,将低于门限的相关参数及字典矩阵相关列置0,当超参数α前后2 次的估计值误差小于10-6或迭代次数大于20 时即可停止迭代。迭代次数的上限20 为经验值,可根据具体实际进行调整。根据相关研究成果,在变分贝叶斯模型中,初始迭代时,βl=1、αm=1/M即可满足收敛性的要求[22],而ρm、δm、al和cl通常设定为接近于0的常数,以防止人为错误参数设置的影响。
表1 列出上述算法各步骤计算量。可以看出,算法运算量主要来自于后验均值、后验协方差矩阵以及门限值的计算。实际处理过程中,随着迭代的进行,通过自动置零操作,能够大大降低矩阵运算维度,对应表中M值将大幅减小,运算复杂度也将随之降低。

表1 算法运算量评估Tab.1 Algorithm computation evaluation
3 算法仿真及结果分析
本节将通过仿真对所提分布式接收多目标信号盲检测算法性能进行分析。仿真条件如下:目标频带范围为80~200 MHz,将目标频带均匀划分为120个网格,对应网格宽度为1 MHz;假设5%的频率网格有信号存在,均为QPSK调制信号,码元速率均为100 kBd,且在不同频率网格随机分布,每个网格至多有1 个信号存在;信号传输增益独立生成,均服从零均值方差为1 的复高斯分布,各接收信号叠加等功率的独立高斯白噪声,不同支路接收的信号平均信噪比相同;以1 GHz 采样率对各接收信号进行数字化采样,并对信号进行分段,数据段长度N=256。
图1为本文所提信号检测算法在不同接收单元数目、不同信噪比下的收敛特性曲线。图中,横坐标为算法迭代次数,纵坐标为信道系数矩阵H的归一化均方根误差。图1中,a)和b)分别为2天线接收和4天线接收的仿真结果。信号带内平均信噪比分别为8、10和12 dB,观测信号长度为256。图中归一化均方根误差曲线为200次独立实验结果的统计平均。从图中可以看出,所提算法通常在4~7次迭代后可实现收敛,且随着信噪比的提升,收敛速度略有降低。而在信噪比SNR=8 dB 时,算法仅需4 次迭代即可收敛;而当信噪比提升至12 dB 时,算法需要6~7 次迭代才能收敛。对比来看,相同信噪比,不同接收单元数目下,算法收敛速度基本相同。
表2 为不同虚警概率预设值下,分别采用2 天线、4天线和8天线接收,本文信号检测算法真实虚警概率统计结果。表中首列为虚警概率预设值,第2~4 列分别为不同接收天线数目下,算法收敛后的虚警概率统计结果,均为真实值。仿真信号带内平均信噪比为5 dB,观测信号长度为256。从结果可以看出,在不同虚警概率预设值下,信号检测算法收敛后真实虚警概率均同预设值相吻合,佐证了本文2.2 节信号检测门限理论推导的正确性。

表2 不同条件下虚警概率预设值与真实值对照表Tab.2 Comparison table of default value and true value of false alarm pobability under dfferent conditions
图2 进一步给出了不同接收单元数目下,本文所提信号检测算法检测概率随虚警概率变化曲线(ROC曲线),仿真条件与表2 仿真条件相同。可以看出,不同接收单元数目下,信号检测概率均随着虚警概率的增加而增加,且在虚警概率一定的条件下,增加接收单元数目,信号检测概率可以获得明显提升,说明所提方法能够实现多个接收信号信息的有效融合,提升信号检测性能。
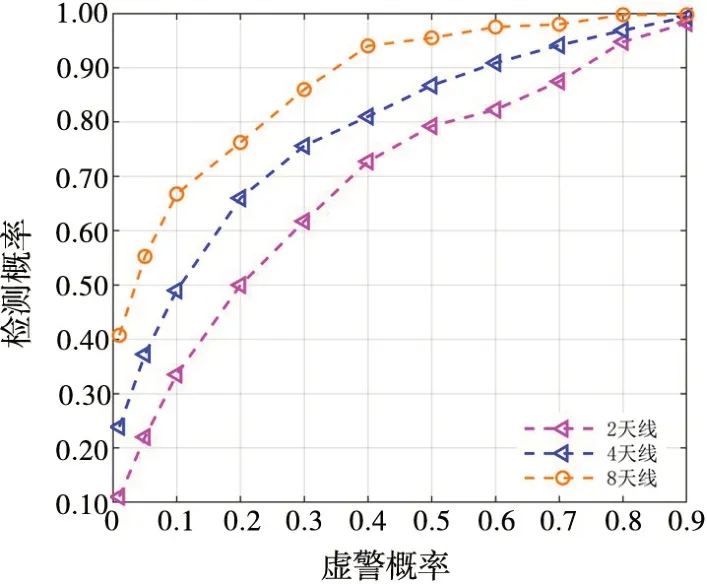
图2 不同接收单元数目下的ROC曲线Fig.2 ROC curve under different number of receiving units
图3、4 分别为虚警概率预设值为0.05 和0.1 条件下,本文信号检测算法收敛后稳态系统性能随信噪比变化曲线,图 a)、b)分别为对应的检测概率和虚警概率的变化曲线。信号长度分别设置为256和512,接收天线数目分别为2和4。从结果可以看出,不同接收单元数目、不同信号长度、不同信噪比下,所提算法虚警概率均能够与预设值保持高度吻合。并且在其他条件相同情形下,通过增加接收单元数目或增加信号长度,算法检测概率均明显提升,且在低信噪比下,该性能提升体现得更加明显。对比4 天线接收(NP=256)和2 天线接收(NP=512),可以看出,在其他条件相同的情况下,将接收单元数目增加1 倍或将信号长度增加1倍,算法检测概率曲线基本重合,证明所提算法可以通过增加接收单元数目,在保证检测性能的前提下,减小对数据长度的要求,有效提升实际短时、突发信号的处理效能。
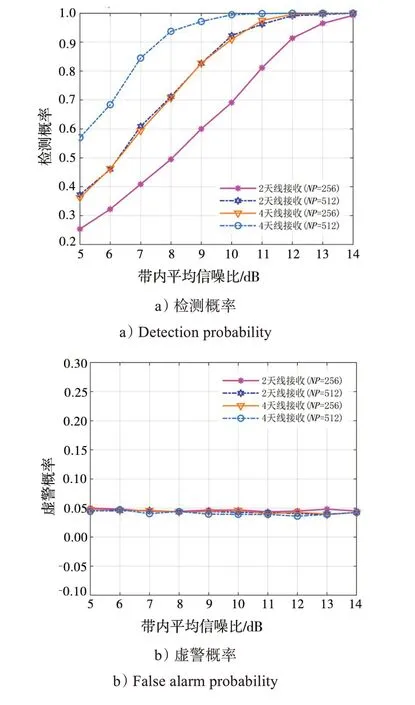
图3 不同条件下算法检测性能随信噪比变化曲线(预设值Pfa=0.05)Fig.3 Curve of algorithm detection performance changing with signal-to-noise ratio under different conditions (preset Pfa=0.05)
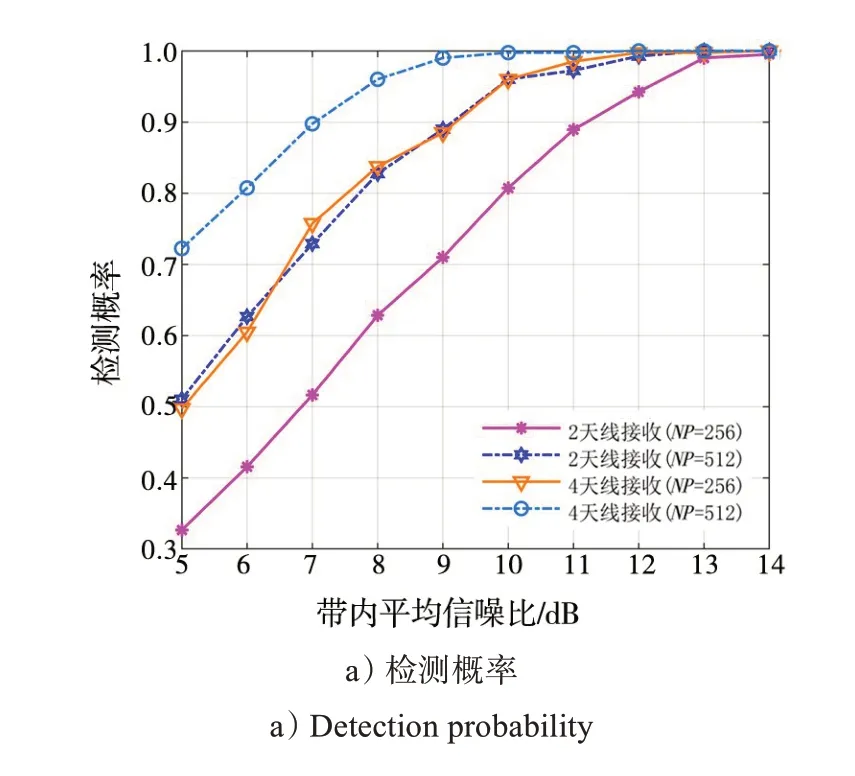
图4 不同条件下算法检测性能随信噪比变化曲线(预设值Pfa=0.1)Fig.4 Curve of algorithm detection performance changing with signal-to-noise ratio under different conditions (preset Pfa=0.1)
图5 为本文算法同基于多传感器融合的稀疏LMS 检测方法[15,23](标注为LMS&VF 方法)的性能对比。LMS&VF方法需要预先设定目标频带信号数目,仿真中,将该值设置为信号数目真实值(实际盲信号检测该值无法提前获知)。本文检测方法虚警概率预设值为0.05,2 种方法所用信号长度均为256,接收天线数目分别设置为2和4。
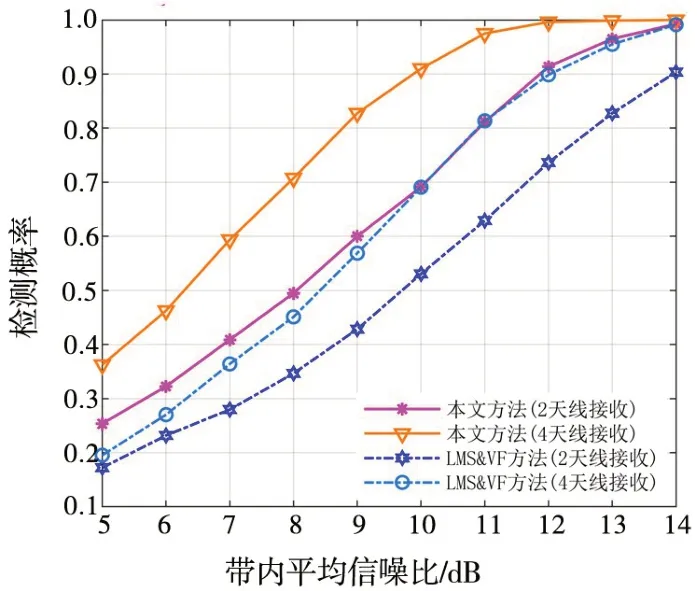
图5 本文方法与LMS&VF方法的性能对比Fig.5 Performance comparison between the proposed method and LMS&VF method
从结果可以看出,随着接收单元数目的增加,2 种方法检测性能均能获得提升,但本文方法性能明显优于LMS&VF方法,且该性能优势在接收单元数目较多(4 天线接收相比于2 天线接收)和信噪比较低时体现得更加明显。在LMS&VF方法中,各接收单元使用稀疏LMS[15]独立进行参数估计,而本文方法在变分贝叶斯框架下使用多个接收信号进行联合参数估计,随着接收单元数目的增加,多天线联合处理体现出明显优势。由图中可以看出,在较低信噪比区间(5~7 dB),增加接收单元数目,LMS&VF 方法难以进行有效融合,而所提算法受此影响较小。需要说明的是,LMS&VF方法需要预设信号数目上限,在实际没有先验信息条件下其性能容易受到影响,而本文算法通过自动置零操作,能够实现特定虚警概率下的未知多目标信号盲检测,实际使用更具灵活性和稳健性。
4 结论
本文针对分布式接收中的宽频带多目标信号检测问题,提出了1种新的多信号盲检测迭代处理方法,其主干为基于变分贝叶斯软信息迭代的多参数联合估计,在每次迭代基础上,利用虚警概率预设值计算信号检测门限,实现多个未知信号的盲检测。理论分析及仿真结果均表明,所提方法在无须预先知道目标频带信号数目及信号频谱位置的情况下,能够实现预设虚警概率下多信号盲检测,与现有方法相比,在接收单元数目较多以及信噪比较低时具有明显优势。文中所提方法主要针对独立分布窄带信号,对于宽带信号模型或信号间不完全独立的情形,则不能直接适用,下一步将对该问题开展进一步深入研究。

