基于自抗扰控制的共轴直升机姿态控制律设计

刘明皓，周沛沅，许敏捷，王新华

（1.中船（北京）智能装备科技有限公司，北京 102629；2.中国船舶集团有限公司第七一六研究所，江苏 连云港 222061；3.南京航空航天大学自动化学院，江苏 南京 210016）

0 引言

共轴直升机在空中飞行和海上着舰过程中，经常受到外部干扰的影响，难以对扰动建立准确的数学模型，且由于其上、下旋翼特殊构型，通道之间存在耦合。无人直升机着舰系统[1]设计的关键问题在于抗扰控制律设计。

受舰船附近大气紊流的干扰，无人直升机机体稳定性差、易受干扰影响的特性会被放大，不利于着舰过程的稳定性，尤其在高海况情况下，外界干扰是影响着舰性能的关键因素[2]。因此，无人直升机控制律应当具备优良的抗扰性能与鲁棒性，这样才能应对海上复杂多变的着舰环境。

目前，工程上使用广泛的直升机着舰控制方法仍是经典PID 控制[3-4]。然而，经典控制方法设计的控制器抗扰性差[5-6]，难以满足着舰过程中对抗扰性的关键要求[7]。针对现代控制方法[7-11]的研究仍然停留在理论研究阶段。自抗扰控制具有能够对受到非线性、时变扰动的不确定系统进行有效控制的特点，因此被广泛应用于受扰动系统中，可利用自抗扰控制的优良抗扰特性，提高着舰过程稳定性[12]。本文选用自抗扰控制设计共轴直升机内环控制律[13]，以提高共轴直升机[14]对外部扰动的抗扰性能；使用改进的粒子群算法，对共轴直升机自抗扰控制律参数进行优化；通过仿真分析说明自抗扰控制律[15-16]的良好性能。

1 共轴无人直升机基本自抗扰控制律设计

1.1 共轴无人直升机建模分析

对共轴无人直升机所受力与力矩进行分析，得到共轴无人直升机运动学模型。共轴无人直升机的线运动方程为：

式（1）中：m为飞行器质量；u、v、w分别为沿OX、OY、OZ轴线速度；p、q、r分别为绕OX、OY、OZ轴角速度。

角运动方程表示为：

式（2）中：Ix、Iy、Iz为直升机对OX、OY、OZ轴的转动惯量；Ixz为直升机对OX和OZ轴的惯性积；∑L、∑M、∑N为绕OX、OY、OZ机体轴转动的力矩之和，绕机体轴正方向转动的力矩为正。

不考虑交叉惯性积可得：

式（3）中：θ、φ分别为俯仰角和滚转角；( )·ur为上旋翼物理量；( )·dr为下旋翼物理量；( )·fus为机身物理量。

针对建立的共轴无人直升机模型，通过开环仿真对其进行自然特性分析。通过MATLAB 软件求得系统17 个开环特征根，其中：4 个特征根虚部为0，实部处于-8.3 附近；4 个特征根位于原点位置；5 个特征根虚部为0，实部处于零点附近；2 个特征根虚部为0，实部为-0.15；2个特征根虚部为0，实部为-0.3；2个特征根对称于虚轴，虚部接近于0，实部为0。整体分析：4个虚部为0，实部处于-8.3 附近的特征根表示横侧向挥舞运动，收敛良好；其余特征根均处在原点位置或者原点附近，状态中立稳定。针对共轴双旋翼直升机输入量与状态量，通过MATLAB软件trim 工具进行配平。配平后的模型零输入状态开环特性各状态量均处于稳定状态。

1.2 自抗扰姿态控制律设计

共轴直升机动力学模型耦合性强，且在海上着舰风扰环境下共轴直升机姿态控制易受扰动影响，ADRC 控制能够避免不同控制通道之间的相互耦合影响。通过估计得到系统总和扰动，通过反馈补偿实现对于扰动的补偿。故针对控制内、外环模型对姿态环滚转、俯仰和偏航通道单独设计ADRC 控制律，在计算控制输出的同时进行反馈补偿，以增强系统鲁棒性与抗扰性。由于ADRC 控制律的分离式原理，故可以对每部分的控制律进行单独设计。

俯仰通道ADRC控制律为例，其结构如图1所示。

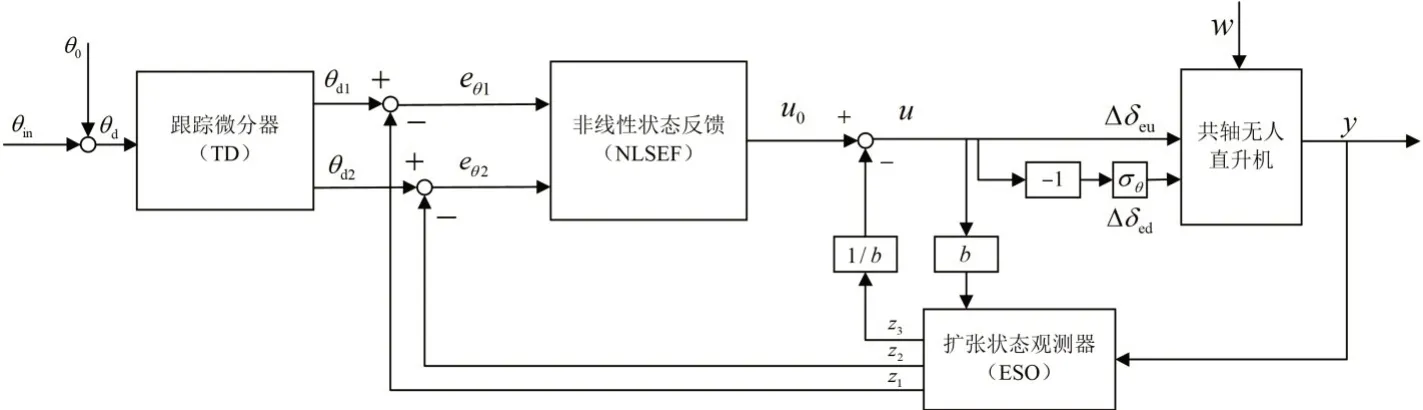
图1 俯仰通道ADRC控制律结构图Fig.1 Structure diagram of pitch channel ADRC control law

建立共轴直升机俯仰通道模型如下：

式（4）中：f( )· 为被控对象俯仰通道所受到的总扰动量，θ1=θ，θ2=θ̇。

对 图1 中 跟 踪 微 分 器（Tracking Differentiator，TD）、扩张状态观测器（Extended State Observer，ESO）以及非线性状态反馈（Nonlinear State Error Feedback，NLSEF）进行如下设计：

1） 跟踪微分器（TD）：

式（5）中，fhan函数为ADRC最速跟踪函数。

通过将输入俯仰角控制量θin与配平俯仰角θ0相加，得到期望的俯仰角θd输入到跟踪微分器以获得期望俯仰角的跟踪信号θd1和跟踪信号的微分信号θd2。式（5）中，r是速度因子，h0是滤波因子，在仿真实验中可以与积分步长h取值相同。

2） 扩张状态观测器（ESO）：

式（6）为俯仰通道扩张状态观测器离散形式。其中，β1、β2、β3为状态观测器的增益系数；α01、α02为非线性因子；δ为滤波因子；b为放大倍数。通过状态观测器调整参数可以得到状态量x1、x2的观测量z1和z2，同时还可以得到扩张状态观测量z3，该观测量表征俯仰通道所受到的总扰动。正是该扩张状态量的实时观测与补偿保证了系统的稳定性。

3） 非线性状态反馈（NLSEF）：

式（7）中：k1、k2为非线性系数；α1、α2与扩张状态观测器中的系数α01、α02均为非线性因子；δ0与扩张状态观测器中的δ均为fal( ·) 函数中的滤波因子；Δδeu和Δδed分别为上、下旋翼的纵向周期变距，通过参考文献可知参数取值范围为0＜α1＜1＜α2。非线性状态反馈通过误差eθ1和eθ2的非线性组合得到u0(T) ，再通过对于扩张观测量z3(T) 的补偿，消除系统扰动对于稳定性的影响，最终得到控制量u(T) 。由于共轴无人直升机的上、下旋翼特殊构型，下旋翼纵向周期变距Δδed与上旋翼纵向周期变距Δδeu方向相反，同时可以通过调整俯仰因子σθ来调整上、下旋翼纵向周期变距对于共轴直升机俯仰运动的控制占比。同理可以得到滚转通道控制律结构和偏航通道控制律结构，ADRC 控制律各部分设计和俯仰通道一致。

2 基于改进粒子群算法的自抗扰控制律参数优化

同PID控制算法中的比例、积分、微分参数大小会对控制算法效果造成影响，ADRC 控制中的参数数值的选取也会对ADRC 控制算法的控制效果造成影响。为了解决参数准确整定的问题，在ADRC 参数整定方面已经有很多智能寻优算法的应用，能够实现参数的自动优化。

粒子群优化算法[17-18]是智能寻优算法中的1 种。它通过种群粒子（初始值随机的解）的群体迭代过程确定目标最优解。整个迭代过程是通过计算得到的“个体极值”和“全局极值”来确定粒子更新的方向。在迭代过程中，当找到这2个极值之后，就可以使用它们对个体的位置与速度进行更新。与其他的优化算法相比，粒子群优化算法具备不需要变异和交叉操作的优点，优化过程中需要设定额定参数和寻优计算量都较小，在大多数情况下可在更短的时间内收敛到所求最优解。

2.1 标准粒子群优化算法

式（8）（9）中：w为惯性权重，其数值大小表示了前一时刻速度在当前速度更新过程中所占的权重。惯性权重的调整能够调整算法对于局部与全局的搜索能力。

标准粒子群算法一般使用式（10）所表示的线性递减形式的惯性权重，其中：wstart、wend为初始值与终止值；tmax为所设置的迭代最大次数。a1、a2分别为自加速系数与全局加速系数，通过这2 个参数来调整迭代过程中从自身最优位置和种群最优位置进行学习的能力。r1、r2都是0～1 范围内的随机数。此时，还需要通过公式中迭代次数为t+2 的速度与位置计算更新t+1迭代次数时的“个体极值”与“全局极值”。

2.2 改进粒子群优化算法

传统粒子群算法存在一定的缺陷，在迭代的过程中会趋向于“全局极值”方向，导致参数优化的过程中容易出现收敛于局部最优解和后期收敛缓慢的问题。为了解决该问题，对算法中惯性权重与加速系数形式进行改进。

对于惯性权重：当其增大时会增强对于全局空间的搜索能力；当其减小时反之，但此时对于局部空间的搜索能力会增加。所以理想惯性权重需要满足系数从大到小的动态变化和系数在前后期减小缓慢这2个条件。通过引入sigmoid 函数对系数进行优化设计。sigmoid函数形式如下：

sigmoid函数值满足单调变化，且在变化初期与变化末期的变化速度减缓，符合惯性权重迭代过程中的变化趋势。借助sigmoid函数对惯性权重设计：

式（14）中：wstart和wend为惯性权重迭代的初始值和终止值；t为迭代次数。当系数b、c取值为3.1 和0.06 时，得到的惯性权重满足理想惯性权重条件，有利于初期全局搜索与后期局部搜索。

在传统的粒子群算法中，加速系数a1、a2是固定不变的常量，与理想搜索状态下前期注重全局搜索能力、后期注重局部搜索能力的要求不相符，故对加速因子a1、a2进行如下设计：

通过在算法迭代过程中不断变化的惯性权重w来进行前后期的区分，用正弦波表示形式平滑参数变化，将加速因子初始值与终止值设置为，得 到 迭 代 过 程 加速系数变化情况如图2、3所示。

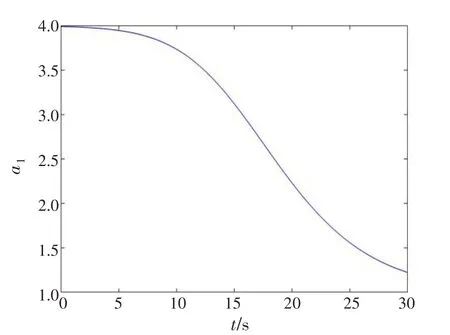
图2 全局加速系数变化曲线图Fig.2 Global acceleration coefficient variation curve

图3 自加速系数变化曲线图Fig.3 Curve plot of self acceleration coefficient change

2.3 自抗扰控制律参数优化

将共轴直升机控制对象的自抗扰控制律与改进粒子群算法相结合，借助粒子群算法快速寻优的特性对自抗扰控制律参数进行优化。改进粒子群算法自抗扰控制律参数优化结构如图4所示。

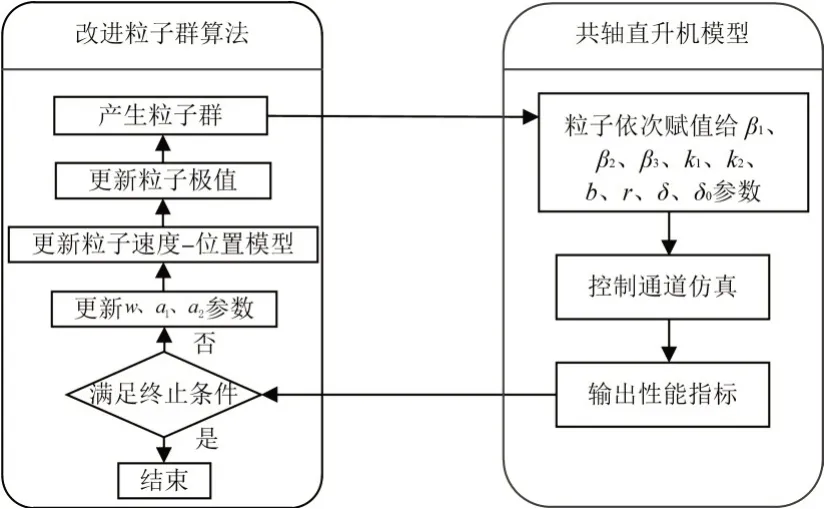
图4 改进粒子群算法自抗扰控制律参数优化结构图Fig.4 Structure diagram of active disturbance rejection control law parameter optimization based on improved particle swarm optimization

粒子群算法参数优化流程如下。

1） 初始化粒子群，对种群规模N，惯性权重w，加速因子a1和a2，迭代终止条件以及粒子初始位置、速度等进行初始化。迭代终止条件可以是对粒子群算法迭代次数的限制，也可以是对性能指标即适应度函数值的限制。

2） 将粒子群中的粒子表示的数据轮流赋值给ADRC 控制律中所需要整定的参数，使用当前参数进行共轴直升机ADRC控制仿真。

3） 通过仿真运行计算性能指标。

4） 当性能指标满足终止条件规定，或者迭代次数满足终止条件规定时，满足结束条件，得到参数最优解。性能指标依据ITAE 准则设计，适应度函数如式（16）所示：

5） 当不满足终止条件，通过式（14）（15）对惯性权重和加速因子进行更新。通过式（8）（9）更新粒子的位置与速度信息。

6） 通过式（11）（12）对粒子的“个体极值”与种群“全局极值”进行更新。

7） 更新后的粒子群转至步骤（2）进行下一轮迭代。

最终优化得出各个通道的自抗扰控制律优化参数如表1 所示。表中：r表示微分跟踪器中的速度因子；δ、b、β1、β2、β3分别表示扩张状态观测器中的增益系数、滤波因子和放大倍数；δ0、k1、k2分别表示非线性状态反馈中的非线性系数和滤波因子。

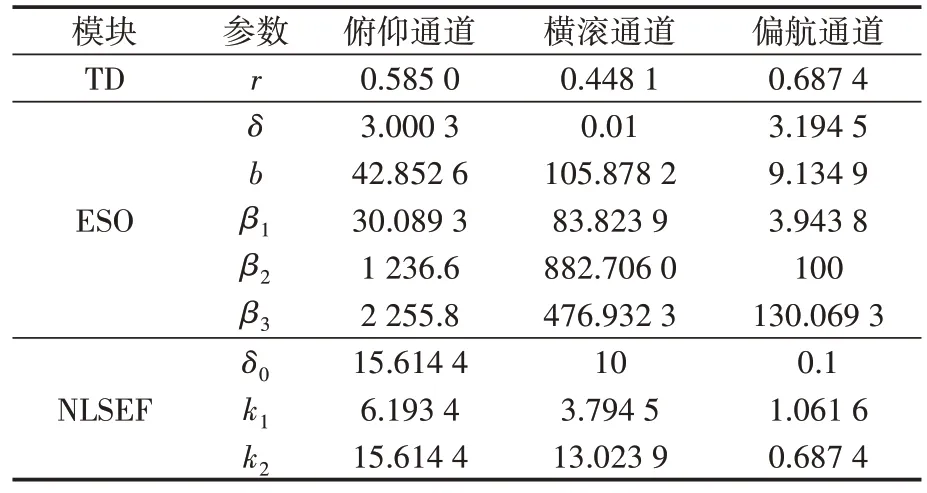
表1 自抗扰控制律优化参数Tab.1 Optimal parameters of active disturbance rejection control law

3 仿真分析

3.1 改进粒子群优化算法性能仿真分析

对共轴直升机模型俯仰通道ADRC 控制器分别使用传统粒子群算法与改进粒子群算法进行参数整定。初始化设置种群规模N=50，粒子纬度C=30，惯性 权 重wmax=0.9、wmin=0.4，加 速 因 子，迭代终止条件为迭代30次，分别得到迭代曲线如图5、6所示。从图可以看出：传统粒子群算法需要进行18次迭代才能达到算法最优解；而改进粒子群算法只需要进行13 次迭代即可达到算法最优解。且传统算法的最优解的适应度值为0.004 3；而改进粒子群算法迭代最优解的适应度值为0.000 41。

图5 标准粒子群优化算法迭代曲线Fig.5 Iterative curve of standard particle swarm optimization algorithm

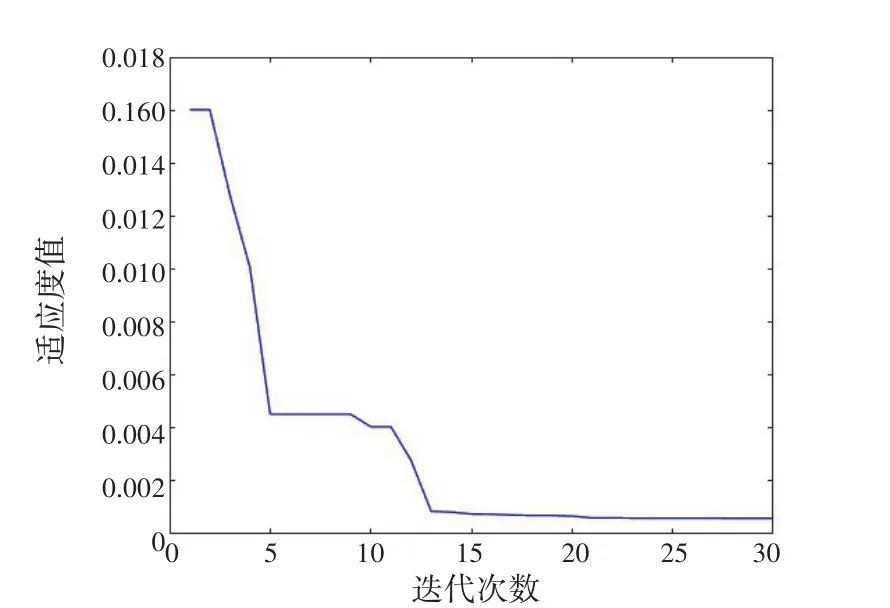
图6 改进粒子群优化算法迭代曲线Fig.6 Iterative curve of improved particle swarm optimization algorithm

经过多次仿真实验统计：传统算法的平均最佳适应度值为4.5×10-3；改进粒子群算法的平均最佳适应度为2.7×10-4。

改进粒子群算法通过对惯性权重和速度因子参数的形式调整，引入sigmoid 函数实现变化趋势单调，且在迭代前期和后期速度减缓的理想参数变化，不仅加强了迭代前期对于全局的搜索能力，使得适应度值收敛速度加快，同时还加强了后期局部空间搜索能力，避免迭代后期出现因为粒子速度过大导致跳过最优解的情况，使得迭代最优解适应度值更低。

3.2 自抗扰姿态控制律性能仿真分析

在共轴直升机姿态控制中常使用PID控制律设计姿态内环控制律。PID控制律主要通过偏差信号的反馈校正实现对输入控制信号的响应跟踪。以俯仰通道为例，将期望俯仰角与实际俯仰角的差值叠加配平俯仰角后，输入到PI控制律。同时考虑到物理微分难以工程实现，将实际俯仰角速率乘以微分系数作为微分环节输出，将上述输出相加得到PID控制律输出eq。考虑到共轴无人直升机构型的特殊性，俯仰通道的输出量为上、下旋翼的纵向周期变距Δδeu和Δδed，Δδed在输出前需要进行反向，俯仰通道PID控制律结构如图7所示。

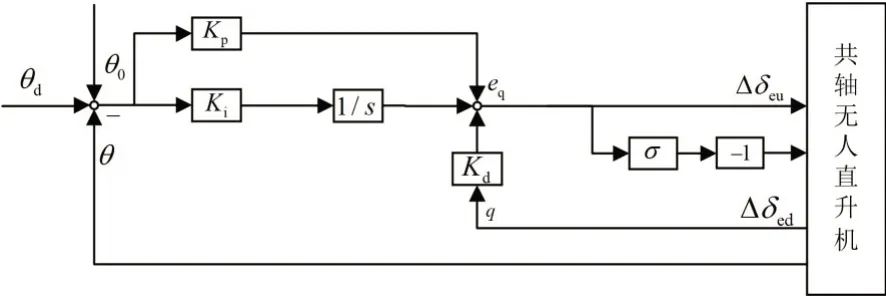
图7 俯仰通道PID控制律结构图Fig.7 PID control law structure diagram of pitch channel

俯仰通道的PID控制律为：

首先，在共轴无人直升机处于稳定悬停状态且无大气紊流等外部扰动的环境下，对PID 姿态控制律与改进ADRC 姿态控制律进行仿真对比。分别对俯仰、偏航、滚转通道在3 s 时输入20°阶跃信号，得到姿态角响应如图8 所示。从仿真结果可以看出，采用PID控制律进行控制时，俯仰角和偏航角响应存在大的超调，需要20 s 的时间来达到稳态，且存在1°s 左右的稳态误差。对于滚转角控制，PID 控制响应相较其他通道效果有所改善，但仍存在稳态误差。采用ADRC 控制通过跟踪微分器安排过渡过程，响应过程更加平滑，几乎不存在稳态误差，响应也更快速。在无外界干扰的理想环境下，ADRC控制较PID控制精度更高，响应速度更快。

图8 无干扰情况下姿态角响应Fig.8 Attitude angle response without interference

由于共轴无人直升机着舰环境复杂多变，所采用的姿态控制律须具备良好的鲁棒性。本文通过在共轴无人直升机纵向周期变距、横向周期变距和总距通道施加气流扰动情况下，分析采用PID 控制与ADRC控制姿态控制律是姿态角对阶跃信号的响应，得到仿真结果如图9 所示。可以看出：当引入气流扰动后，PID 控制器的响应输出曲线有着明显的抖动，在气流扰动环境下PID 控制器控制效果不佳，用于着舰内环姿态控制会影响安全着舰过程；而ADRC 控制器由于扩张观测器对于系统总扰动的观测能力与扰动补偿设计对气流扰动有很强的抗干扰能力，控制效果更佳，具备更强的鲁棒性。

图9 施加气流扰动后姿态角响应Fig.9 Attitude angle response after airflow disturbance

4 结论

本文采用自抗扰控制器对共轴无人直升机姿态控制进行设计，针对自抗扰控制器整定参数过多问题，将改进粒子群算法用于参数优化环节，实现参数的自动优化。通过仿真验证了改进粒子群算法相较于传统粒子群算法寻优参数性能更佳；通过将整定参数后的自抗扰姿态控制器与PID姿态控制器进行仿真对比，结果表明自抗扰控制具备更好的动态性能，且对于以大气紊流为代表的外界扰动具备更好的抗扰性与鲁棒性。