基于工业摄影测量的地下水开采地面沉降试验研究

屈吉鸿, 郭威, 杨莉, 张艺潆

(1.华北水利水电大学 地球科学与工程学院,河南 郑州 450046;2.黄河流域水资源高效利用省部共建协同创新中心,河南 郑州 450046)

地面沉降是一种由多种因素引起的地面标高缓慢降低的环境地质灾害[1]。地面沉降最早由Roberto Gayol发现于19世纪末的墨西哥地区[2]。泰国曼谷地区20世纪80年代初地面沉降速率达到120 mm/年[3]。意大利拉文纳地区二战后地面沉降速度急剧增加到110 mm/年[4]。20世纪50年代末日本西部Chikugo-Saga平原地面沉降面积达328 km2[5]。我国有超过17个省、96个城市出现了明显的地面沉降现象[6]。华北平原是世界上超采地下水导致地面沉降量最大、沉降面积最大的地区[7],北京因地下水超采最大,沉降速率达60 mm/年[8],天津因地下水过度开采导致地面沉降量累计超过1 000 mm[9]。

对地面沉降进行快速、准确的监测是研究地面沉降演化规律、制定控制对策的基础。BALDI P等[10]利用GPS对意大利半岛中北部平原进行监测,发现波河平原中部的沉降速率约为15 mm/年;葛大庆等[11]基于相干点目标的多基线D-InSAR技术监测分析了沧州地区地面沉降速率及演变特征;贺同江等[12]利用GNSS技术研究了天津市地面沉降的变化趋势。随着经济社会的快速发展,郑州市区已形成多个沉降区[13]。王金娜等[14]基于HNGICS开展郑汴洛地区的GNSS地面沉降监测,为郑汴洛地区的地面沉降减灾提供数据支持;王毅[15]利用短基线集干涉测量SBAS技术提取了郑州市2015年至2017年的地面沉降量;王义梅等[16]、汪宝存等[17]、管力等[18]利用合成孔径雷达干涉测量(Synthetic Aperture Radar Interferometry,InSAR)技术分析了郑州市地面沉降的时空变化特征;朱卫民等[19]、詹学启等[20]、夏飞雪等[21]分析了京广高速铁路郑州段发生地面沉降灾害的主要原因;师刚等[22]基于Peck公式建立了郑州典型区双线隧道地面沉降模型;孙伟良等[23]采用三维有限元仿真技术研究了新郑至郑州城际铁路下穿南水北调中线干渠的隧道衬砌的沉降规律。

室内试验是研究地面沉降机理的重要手段,但多采用沉降标尺等传统设备进行沉降监测[24-25]。近景工业摄影测量作为一种快速三维测量工具,相比传统测量设备具有测量精度高、不受环境影响等优点,越来越多地被应用在工业和工程领域,例如航空航天飞行器校准与检验[26]、工业汽车部件[27]、工业产品表面微形变[28]、变形考古挖掘[29]、船体大型复杂管廊模块对接[30]、南水北调工程边坡横断面监测[31]。

地下水开采是诱发郑州市区地面沉降的重要原因,本文结合郑州市区地层岩性,设计了一套具有地下水补给、开采、数据监测和采集等功能且适用于地下水开采条件下的地面沉降物理模拟试验系统,采用MPS工业摄影测量对土体变形进行监测,研究不同地下水补给、开采条件下土体变形的过程和特征,为研究区预防和控制地面沉降提供科学依据。

1 研究方法及试验方案

1.1 MPS工业摄影测量基本原理

工业摄影测量又称数字近景工业摄影测量,是精密工程领域中一项重要技术,通过相机对被测物体从不同位置进行拍摄,得到被测物体两张以上的图像,利用摄影测量原理计算出物体表面测点的三维坐标,进而得到该物体的形状和位置等信息[32]。MPS工业摄影测量属于数字近景工业摄影测量的一种,分为MPS/S单相机摄影测量和MPS/M多相机摄影测量,本试验采用MPS/S单相机摄影测量,该设备测量精度为3 μm+3 ppm·L。

基于单相机的工业摄影测量是利用一台相机在两个或两个以上不同的拍摄位置对同一被测物体进行拍摄,以获得被测目标物两张或多张不同角度的相片,构成被测目标物体一个或多个立体像对(模型)[33],原理如图1所示。

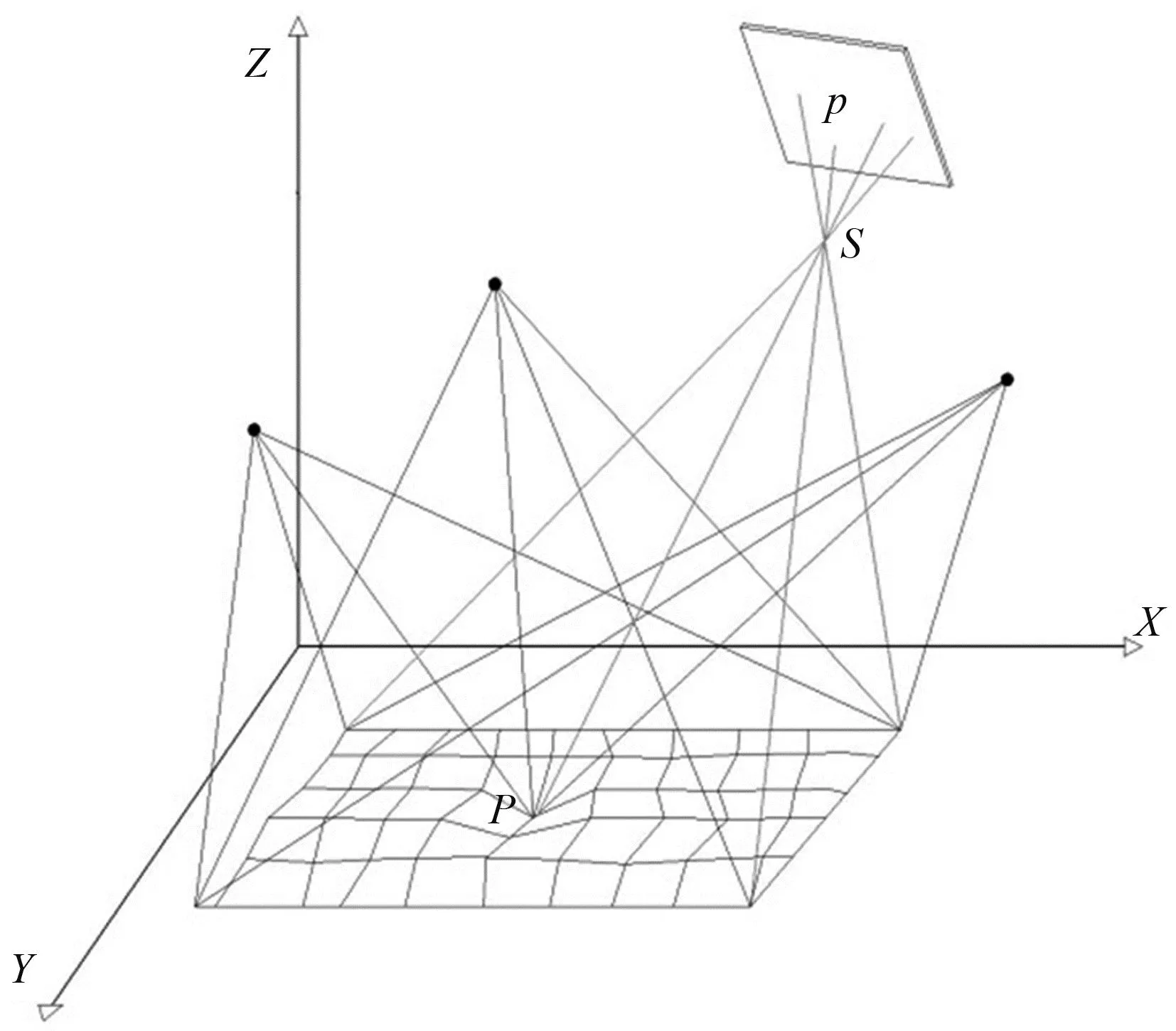
图1 MPS工业摄影测量原理

图1中:P为空间物方点;p为像平面上的像点;S为投影中心,即相机镜头的光学中心。依据最小二乘平差原理,每个光线(束)根据式(1)进行求解,得到被测物体物方点的三维坐标(Xi,Yi,Zi)。三维坐标被获取后,将其导入图形化工业测量系统软件Spatial Analyzer中进行处理,完成形位监测、变形监测、三维控制网测量等。

(1)

式中:(xij,yij)为第j张相片的各像点的理论位置坐标;x0j、y0j、fj为第j张相片的内方位线元素,分别代表像主点与主距,是确定相机镜头中心相对于影像位置关系的参数;(Δxij,Δyij)分别为各像点坐标相对其理论位置坐标(xij、yij)的偏差;(Xi,Yi,Zi)为物方点P在物方坐标系中的坐标;(XSj,YSj,ZSj)为第j张相片的外方位线元素,为相机在瞬间拍摄时的位置;aij、bij、cij(i=1、2、3)分别为第j张相片的3个外方位角元素φj、ωj、κj所组成的9个方向余弦。

1.2 试验系统

试验系统主要包括模型箱体、补给系统、抽水系统、水循环系统、数据采集系统等,如图2和图3所示。①模型箱体尺寸为2 000 mm×500 mm×1 200 mm,箱体上部为土体箱槽,下部为供水循环的水池;箱槽左右侧面分别设有进水装置,箱槽中部设有抽水井。②补给系统设置独立的可调节边界水位的进水装置,以满足不同补给条件。③抽水系统由蠕动泵和抽水井组成,抽水井由不锈钢过滤筛网弯曲成半圆柱空心结构,并在弧面外侧用200目的过滤纱网包裹。④水循环系统:将试验过程中由蠕动泵从砂层中抽出的水通过软管排放至箱体下部的水池,并通过水泵将水池中的水泵至补给系统的水箱,实现水循环。⑤数据采集系统包括MPS工业摄影测量系统、分层水压力计、分层土压力计、分层沉降标尺等。MPS工业摄影测量系统用于监测正面观察窗位置处的土体变形,分层水压力计、土压力计分别测量土层不同位置的水压力和土压力,分层沉降标尺用于监测土体内部变形。

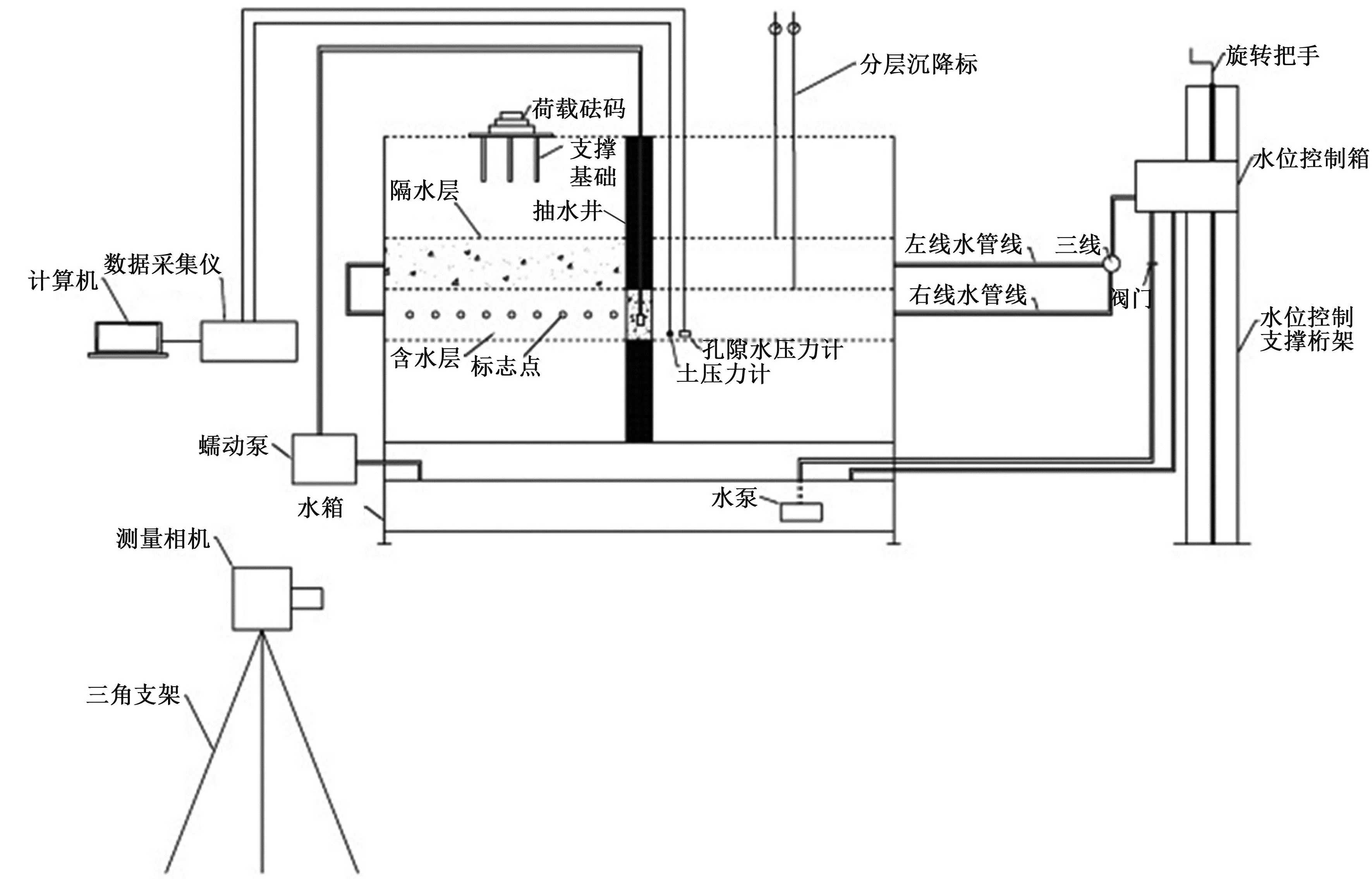
图2 试验系统示意

图3 试验装置

1.3 试验方案

1.3.1 野外取样和土层装填

模拟试验土样采自郑州市西史赵村附近,该区域是郑州市地面沉降最为严重的区域之一,通过钻井取样(图4),并开展土工试验获得土体参数。土样采集区的地层岩性为:0～90 m深度为亚黏土,90～130 m深度为砂砾石,130～210 m深度为亚黏土,210～350 m深度为砂砾石。试验槽填装按照1∶350的比例开展,将土层概化为4层,自下而上依次为:第二承压含水层(砂层,厚度400 mm)、第二黏土层(隔水层,厚度250 mm)、第一承压含水层(砂层,厚度100 mm)、第一黏土层(隔水层,厚度250 mm)。

图4 试验用土取样区

对砂土及黏土试样分别处理备用,其中铺设砂土含水层时,由下向上均匀摊铺,每隔5 cm摊铺一次,铺设完成后,打开抽水泵,将进水管线上的阀门调整为较小状态,确保水流以恒定流速从补给水箱经导水管缓慢注入试验槽中的含水层,当补给水箱中的水位不再下降,孔隙水压力变化率≤0.05 kPa/d时,认为含水层中孔隙水压力达到了饱和状态。为防止注水时土中气体破坏土层结构,在注水前打开排气孔,排除气体;铺设黏土隔水层时,每5 cm摊铺一层,采用边制样边铺设的方法,确保土体完整,土体中无较大的贯通孔隙。

1.3.2 监测设备铺设

在MPS测量标志点铺设过程中,在观察窗内壁均匀涂抹凡士林,以消除边界效应。试验箱槽内部铺设土压力计、水压力计、沉降标尺等数据传感器。

试验箱槽以抽水井为对称轴,左右分别竖向分割成4部分共16个研究区域,每个研究区域铺设了5个MPS标志点,共80个MPS标志点,从下往上MPS标志点分别记为A1—A20、B1—B20、C1—C20和D1—D20,如图5所示。

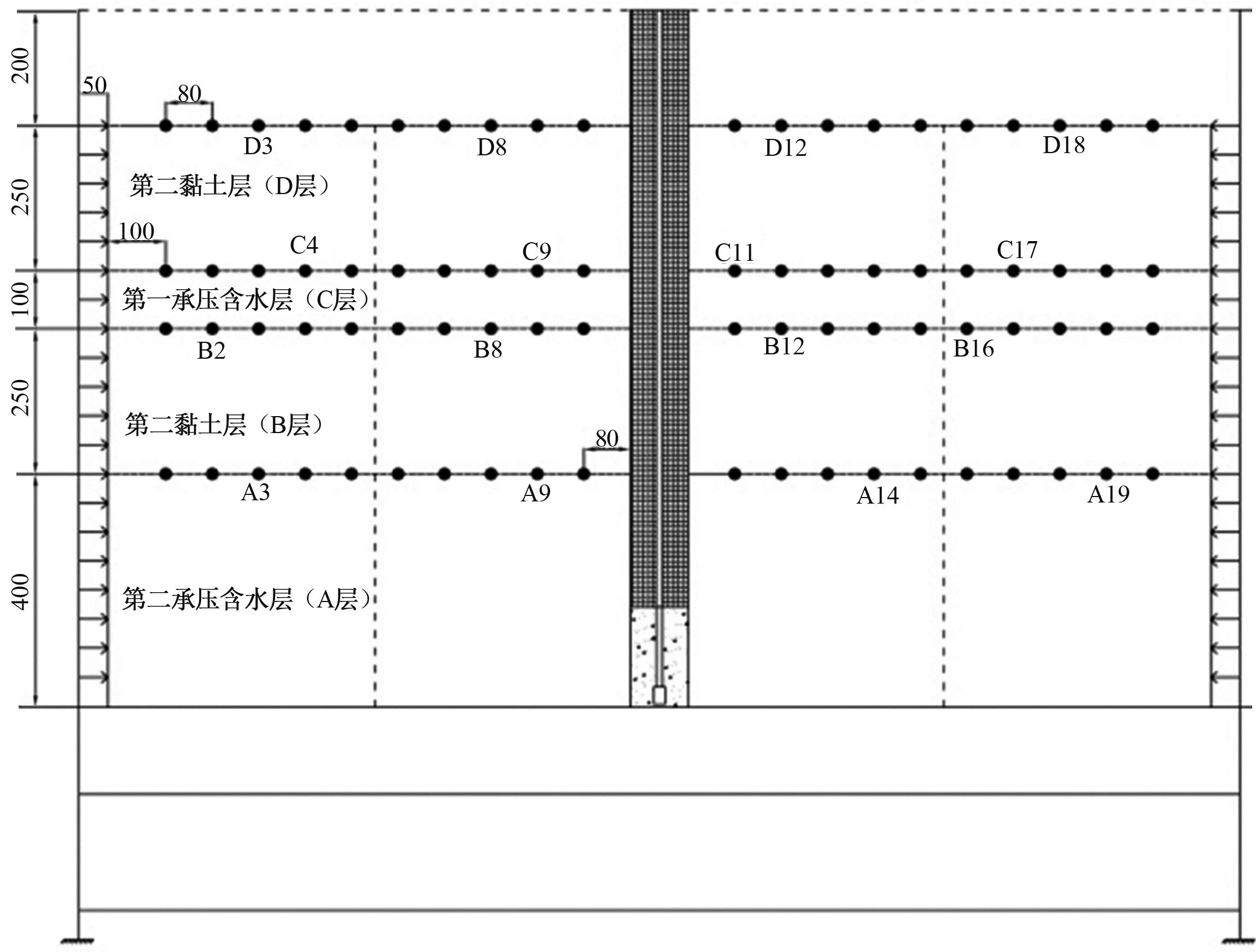
图5 分层MPS标志点布设示意(单位:mm)

试验箱槽内部每层布设3个沉降标尺,并均布设在箱体中轴线上,即均距正面观察窗25 cm,从下往上,第二承压含水层沉降标尺标记为a1—a3,第二黏土层沉降标尺标记为b1—b3,第一承压含水层沉降标尺标记为c1—c3,第一黏土层沉降标尺标记d1—d3,如图6所示。

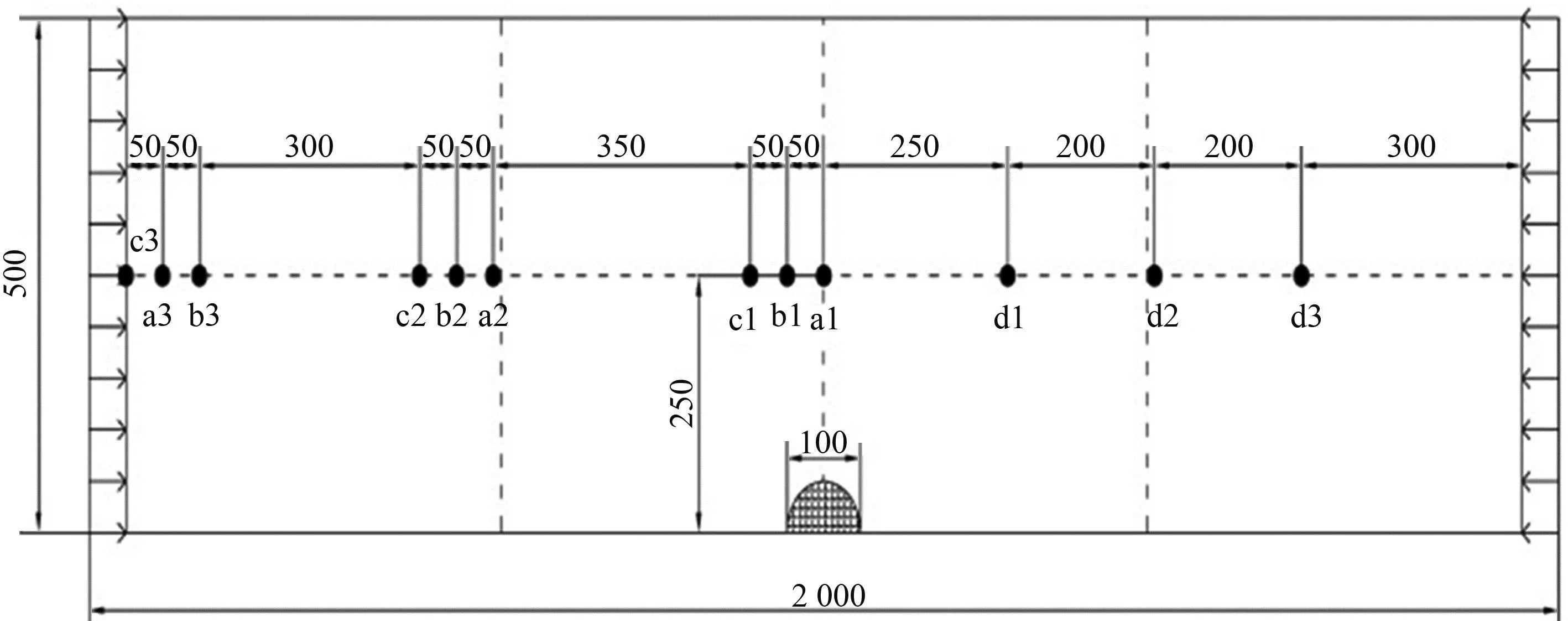
图6 分层沉降标尺布设示意(单位:mm)

1.3.3 试验过程

根据取土样区域近10年地下水位情况,在满足含水层承压和抽水井不向外溢流的前提下,经预试验得知第二承压含水层水位为750 mm。本次沉降试验仅对第二承压含水层在定水头边界和变水头边界两种工况开展研究。

1)定水头边界工况。通过供水系统,保持左、右边界水位不变,先逐级增大抽水井抽水速率,以模拟实际地下水开采量增加的情况,后逐级减小抽水速率以模拟现实中地下水开采量减少的情况。基于预试验分析,抽水速率从0 mL/min逐级递增至4 000 mL/min,后逐级降至0 mL/min,即0、1 000、2 000、3 000、4 000、3 000、2 000、1 000、500、0 mL/min,每级抽水时间12 h、间隔2 h。抽水结束后,观察沉降标尺、标志点、水压力计、土压力计等监测数据直至相对稳定。

2)变水头边界工况。边界处停止供水,抽水井抽水速率从1 200 mL/min逐级递减至0 mL/min,即1 200、900、600、300、0 mL/min,每级抽水时间10 h、间隔4 h。抽水结束后,观察沉降标尺、MPS标志点、水压力计等监测数据,当孔隙水压力变化率≤0.05 kPa/d、土体各土层形变量变化率≤0.01 mm/d时,认为土体固结达到稳定状态。

1.4 MPS数据处理

首先,将拍摄的每组照片、基准尺文件导入解算软件,通过自动测量、平差后,选取固定点,剔除杂点。然后,利用光束法平差,得到各层标志点的三维坐标。最后,将两次拍摄照片解算后得到两组三维坐标,利用Spatial Analyzer软件最佳拟合转化,重新建立坐标系,得到两组三维坐标数据的变化量,即土体变形量。试验后MPS标志点位移如图7所示,图7中箭头指向代表标志点位移方向,即土体变形方向,箭线长度表示标志点位移量。在此次研究中,仅采用标志点的垂直位移量。

图7 试验后MPS标志点位移示意

2 结果分析

2.1 基于MPS测量的沉降特征

2.1.1 抽水井附近沉降特征

为分析定水头边界和变水头边界工况下抽水井附近土体的沉降特征,选取抽水井附近标志点的观测数据,绘制沉降变化过程线,如图8所示。图8中,无论是定水头边界工况阶段([0,156]h),还是变水头边界工况阶段((156,350]h),各土层沉降均呈现起伏波动变化的特征,土层沉降随时间增加,且在空间上存在明显的滞后效应。

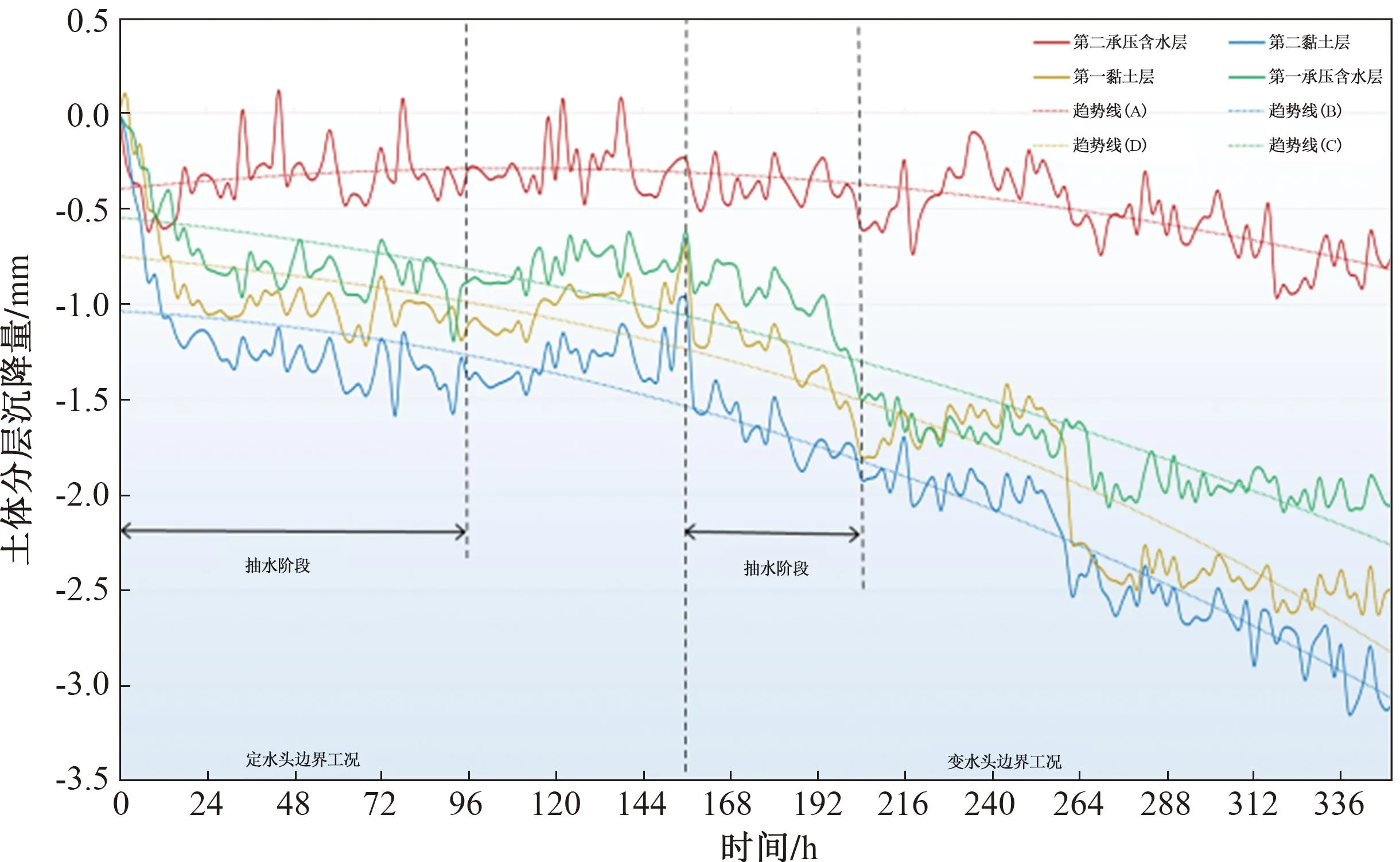
图8 不同工况下各土层变形曲线

1)定水头边界工况。抽水结束时(96 h),土层从下向上,第二承压含水层(A层)、第二黏土层(B层)、第一承压含水层(C层)、第一层黏土层(D层)分别沉降0.294、1.391、0.882、1.108 mm。静置结束时(156 h),A层、B层、C层、D层分别沉降0.245、0.977、0.625、0.711 mm,土层有所回弹,沉降量分别较抽水结束时减少17%、30%、29%和36%。

2)变水头边界工况。抽水结束时(208 h),A层、B层、C层、D层分别沉降0.601、1.911、1.471、1.798 mm,沉降量分别较抽水前增加145%、96%、135%、153%。静置结束时(350 h),A层、B层、C层、D层分别沉降0.751、3.098、2.057、2.487 mm,沉降量分别较抽水结束时增加25%、62%、40%、38%。

由上述可知,无论定水头边界工况还是变水头边界工况,各土层沉降量均呈现起伏波动变化的特征。在定水头边界工况下,抽水结束后,土层有所回弹;变水头边界工况下,抽水结束后各土层沉降继续发展,相比定水头边界工况,抽水导致的土层沉降变化明显。

2.1.2 各土层沉降特征

分别在第二承压含水层(A层)、第二黏土层(B层)、第一承压含水层(C层)和第一黏土层(D层)中选择4个典型位置的MPS标志点进行分层沉降特征分析,标志点位置如图5所示。观测到的沉降量见表1,沉降变化过程如图9—12所示。

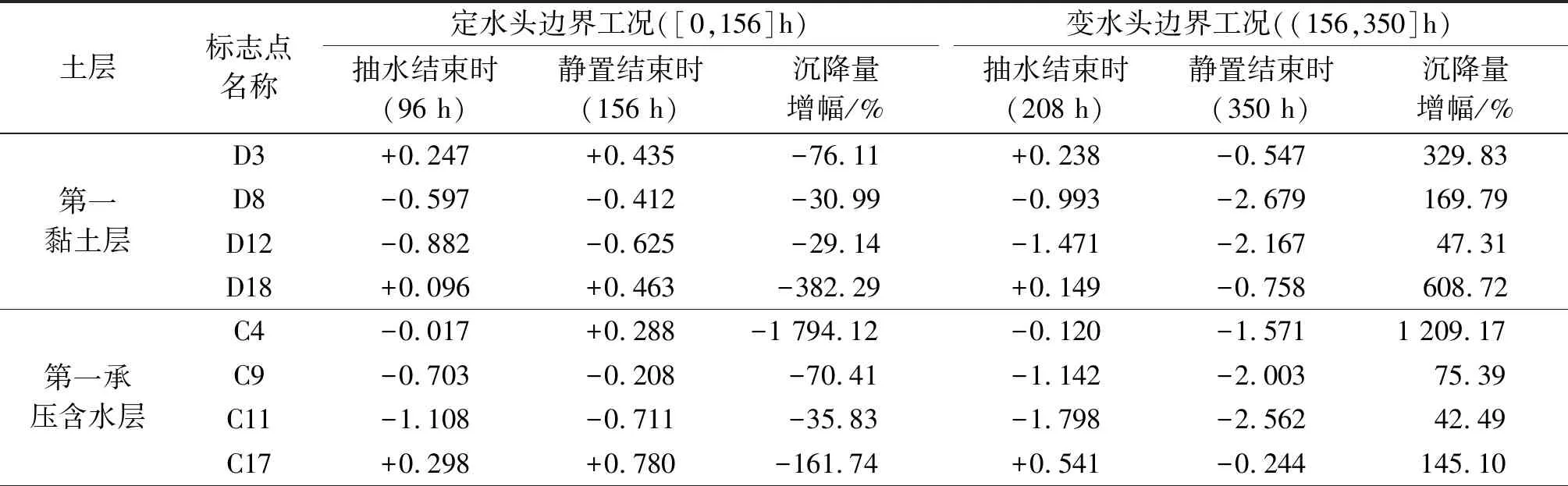
表1 各土层主要标志点沉降量 mm

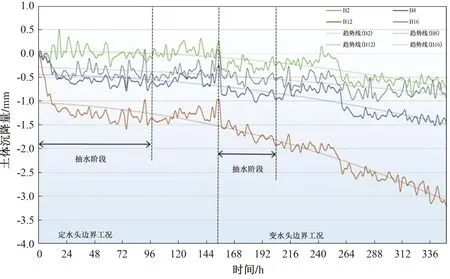
图9 第二黏土层沉降过程线(标志点)

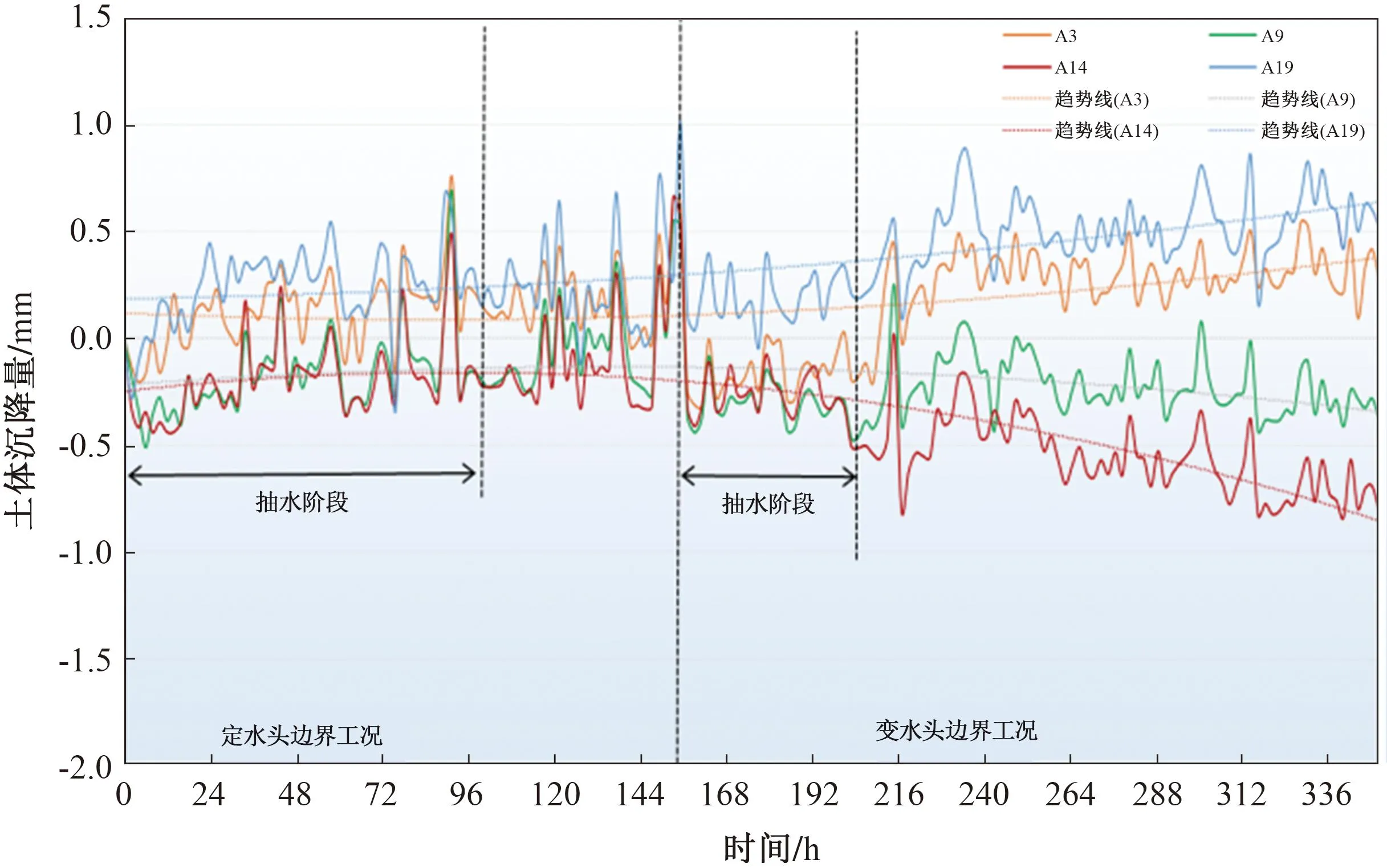
图10 第二承压含水层沉降过程线(标志点)

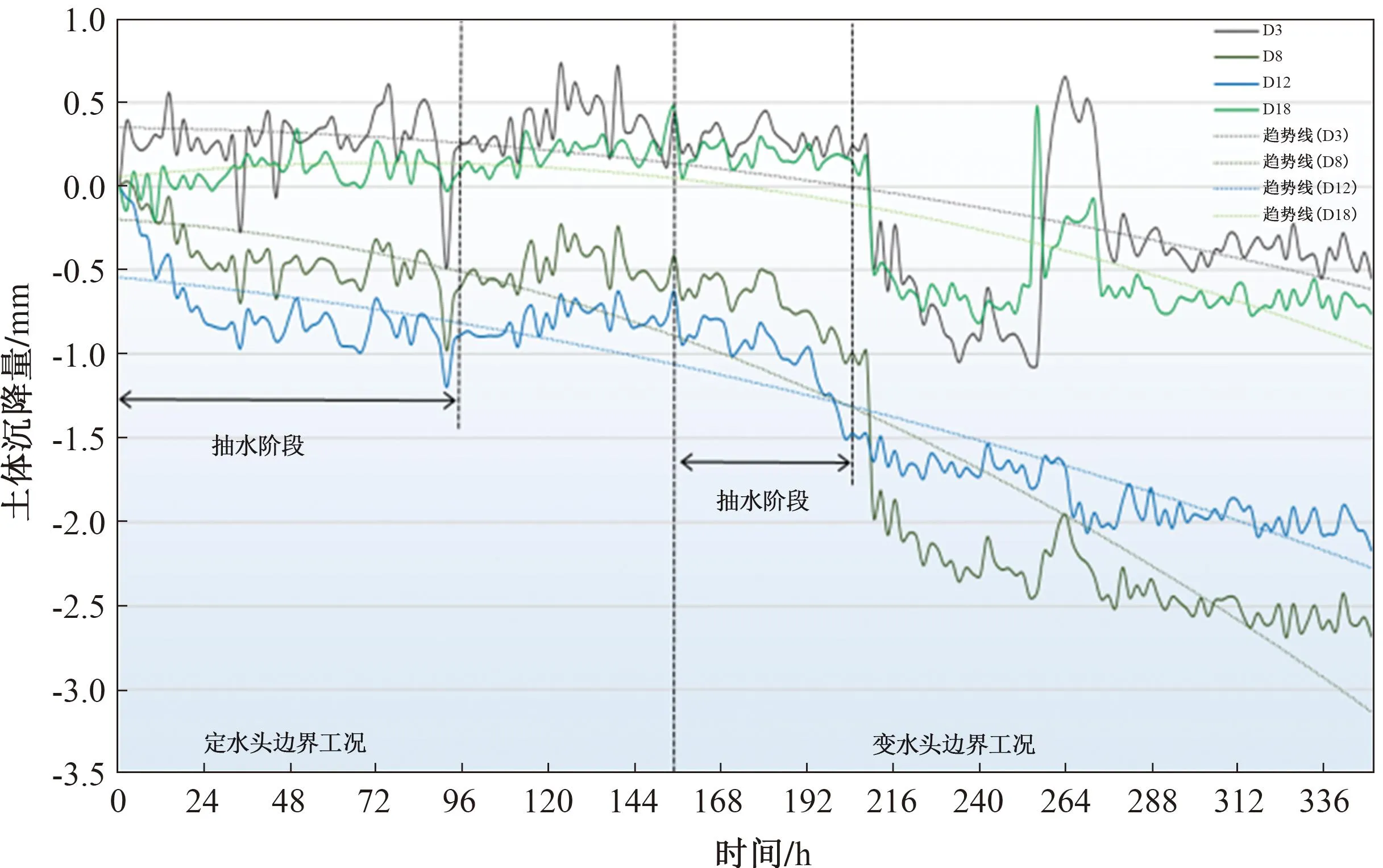
图11 第一黏土层沉降过程线(标志点)

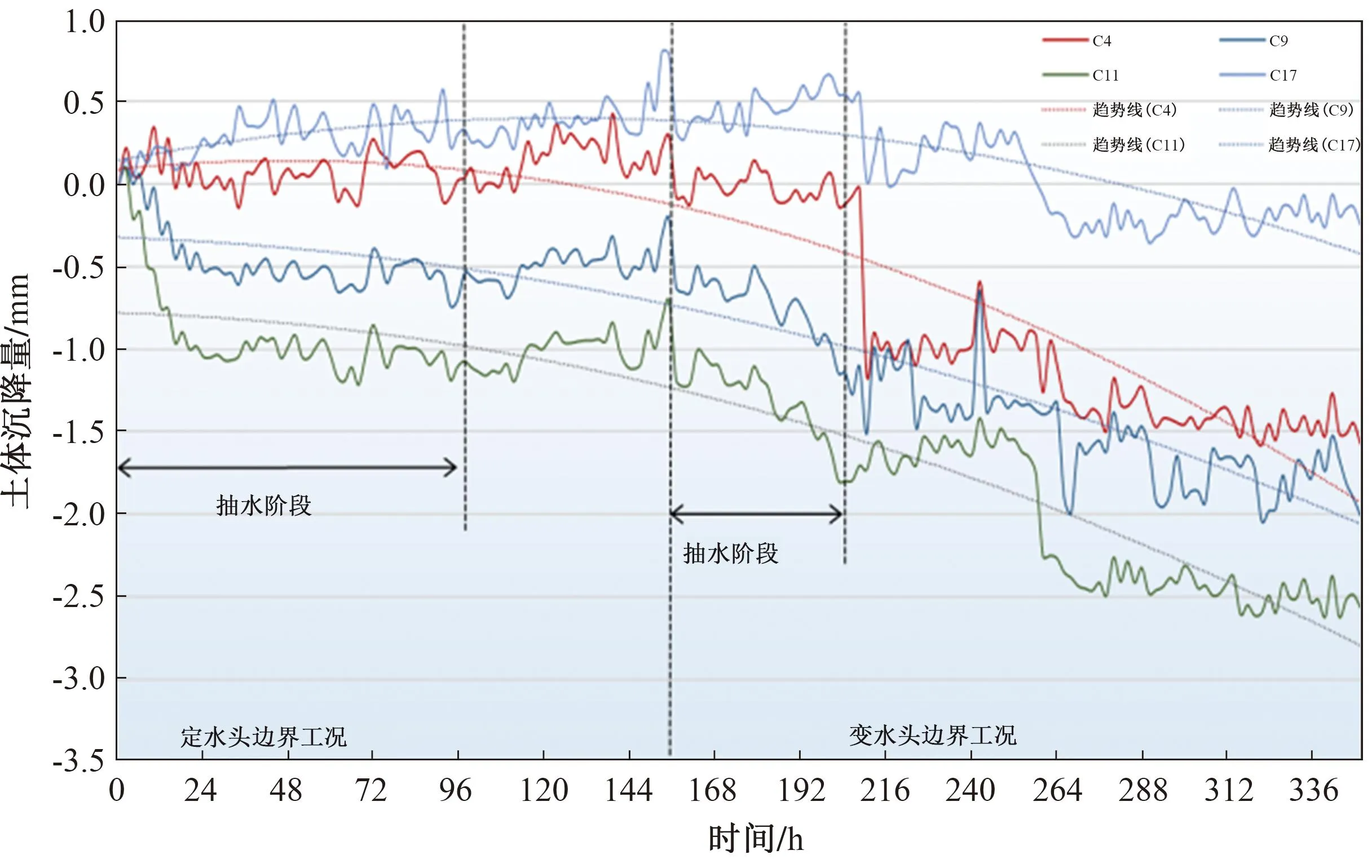
图12 第一承压含水层沉降过程线(标志点)

由表1和图9—12可知:

1)第二承压含水层中选取A3、A9、A14和A19标志点进行沉降分析。A3标志点距抽水井69 cm,距左侧供水孔26 cm,定水头边界工况下,抽水后土体抬升0.229 mm,静置结束时,土体抬升0.632 mm;变水头边界工况下,抽水后土体沉降-0.182 mm,静置结束时,土体抬升0.269 mm。A9标志点距抽水井21 cm,距左侧供水孔74 cm,定水头边界工况下,抽水后土体沉降-0.174 mm,静置结束时,土体抬升0.527 mm;变水头边界工况下,抽水后土体沉降-0.461 mm,静置结束时,沉降-0.385 mm。A14标志点距抽水井37 cm,距右侧供水孔58 cm,定水头边界工况下,抽水后土体沉降-0.146 mm,静置结束时,土体抬升0.552 mm;变水头边界工况下,抽水后土体沉降-0.515 mm,静置结束时,土体沉降-0.812 mm。A19标志点距抽水井77 cm,距右侧供水孔18 cm,定水头边界工况下,抽水后土体抬升0.305 mm,静置结束时,土体抬升1.011 mm;变水头边界工况下,抽水后土体抬升0.186 mm,静置结束时,土体抬升0.518 mm。

2)在定水头和变水头两种边界工况下,第二黏土层B8和B12标志点的沉降量大于B2和B16标志点的沉降量;第一承压含水层C9和C11标志点的沉降量大于C4和C17标志点的沉降量;第一黏土层D8和D12标志点的沉降量大于D3和D18标志点的沉降量。结合标志点位置(图5)可知,同一土层中标志点距抽水井距离越近,其沉降量越大,但沉降量与距抽水井距离不成正比。在定水头边界工况下,抽水静置后各土层中各标志点均有不同程度的抬升,在变水头边界工况下,抽水静置后,各土层中各标志点沉降量持续增大。

2.2 基于沉降标尺测量的沉降特征

2.2.1 抽水井附近沉降特征

为分析抽水井附近各土层土体内部的沉降特征,分别在第二承压含水层、第二黏土层、第一承压含水层、第一黏土层中选择沉降标尺a2、b2、c2、d2,位置如图6所示,其沉降变化过程如图13所示。

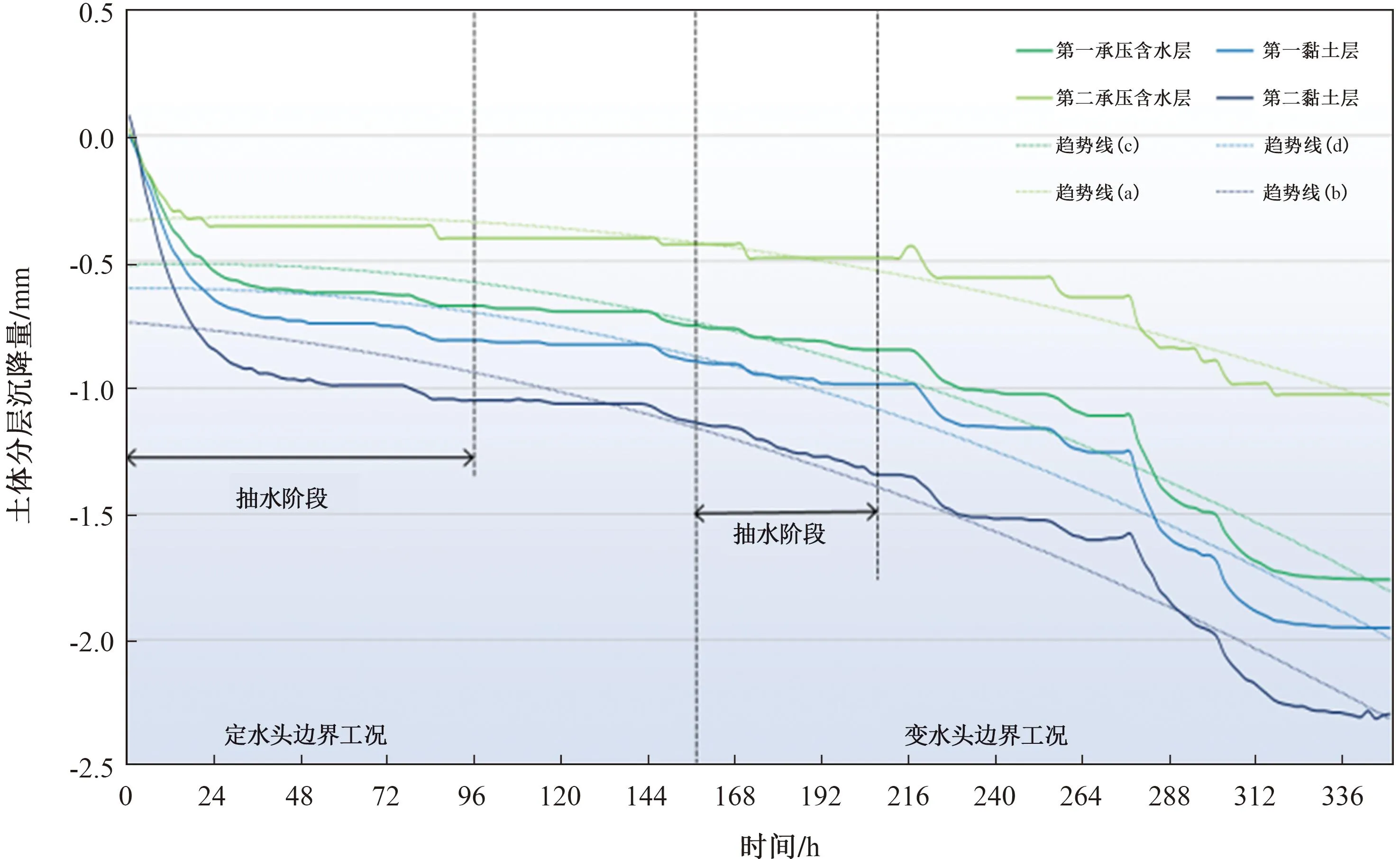
图13 抽水井附近土体内部沉降变化量

由图13可知:

1)无论是在定水头边界工况([0,156]h),还是在变水头边界工况((156,350]h),抽水井附近各层土体内部沉降变化趋势与抽水井附近MPS标志点的沉降变化趋势相同。

2)定水头边界工况。抽水结束时(96 h),土层从下向上,抽水井附近的a2、b2、c2、d2处分别沉降0.408、1.050、0.676、0.812 mm。静置结束时(156 h),a2、b2、c2、d2处分别沉降0.432、1.134、0.755、0.893 mm,与抽水结束时相比,沉降量分别增加6%、8%、12%和10%。

3)变水头边界工况。抽水结束时(208 h),a2、b2、c2、d2处分别沉降0.486、1.338、0.850、0.986 mm,沉降量分别较抽水前增加13%、18%、13%、10%。静置结束时(350 h),a2、b2、c2、d2处分别沉降1.026、2.292、1.760、1.952 mm,与抽水结束时相比,沉降量分别增加138%、102%、133%和118%。

由试验装置可知,沉降标尺测量的沉降是土体内部沉降,而MPS测量的沉降是土体侧面沉降。由MPS测量的总体沉降特征可知:在变水头边界工况下土体沉降主要发生在抽水过程中;而由沉降标尺测量的总体沉降特征可知,在变水头边界工况下土体沉降主要发生在静置过程中,即侧面沉降发生在抽水阶段,内部沉降发生在静置阶段。主要原因是土体内部的沉降标尺较标志点距抽水井远,沉降从抽水井处开始发生,并不断向外扩散,传递至土体内部需要一定的时间,表明土体内部沉降存在滞后性。

2.2.2 各土层沉降特征

分别在第二承压含水层(A层)、第二黏土层(B层)、第一承压含水层(C层)和第一黏土层(D层)中选择3个典型位置的沉降标尺进行分层沉降特征分析,沉降标尺位置如图6所示。通过沉降标尺测量到的土层内部沉降量见表2,沉降变化过程如图14—17所示。

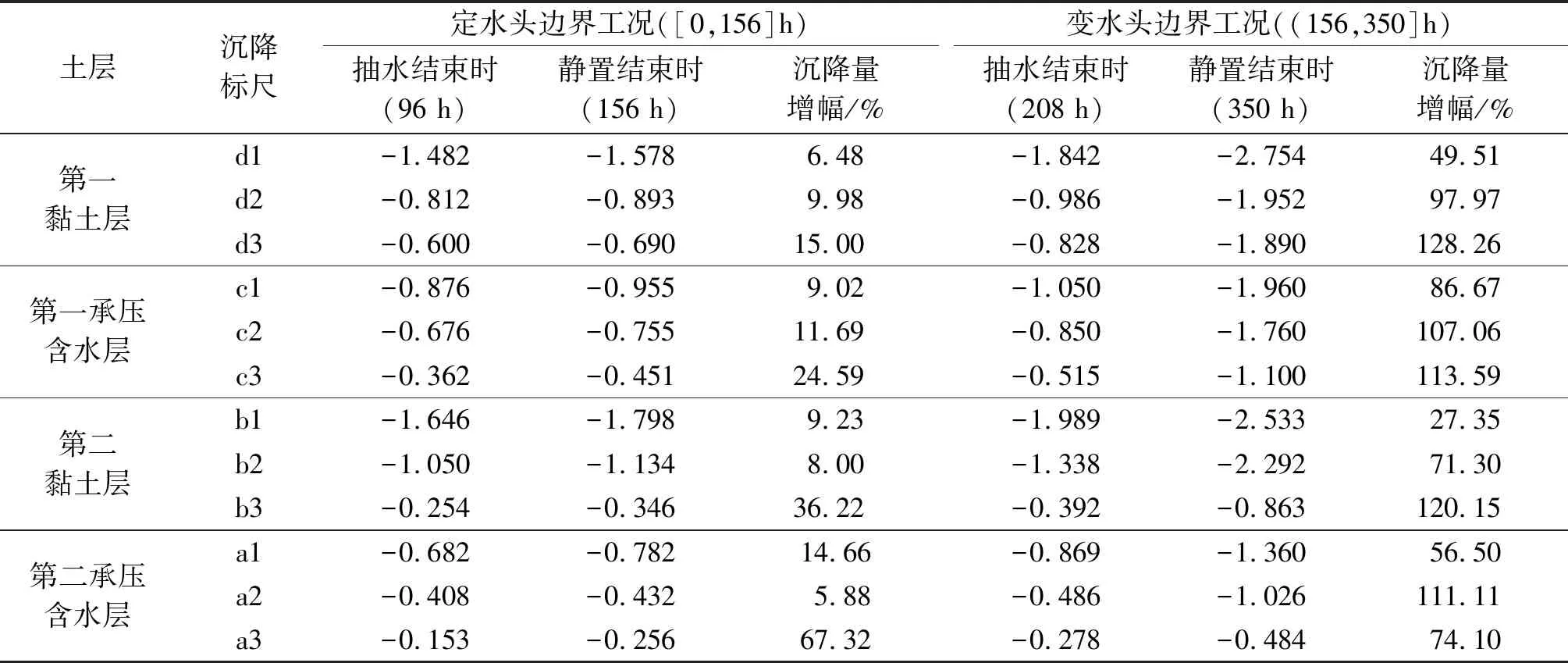
表2 各层沉降标尺沉降量 mm

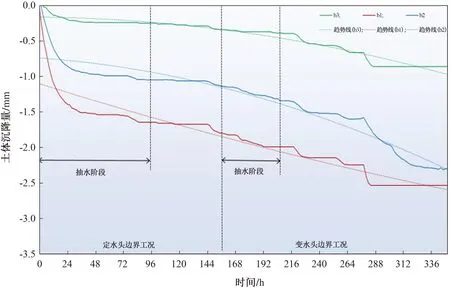
图14 第二黏土层沉降过程线(沉降标尺)

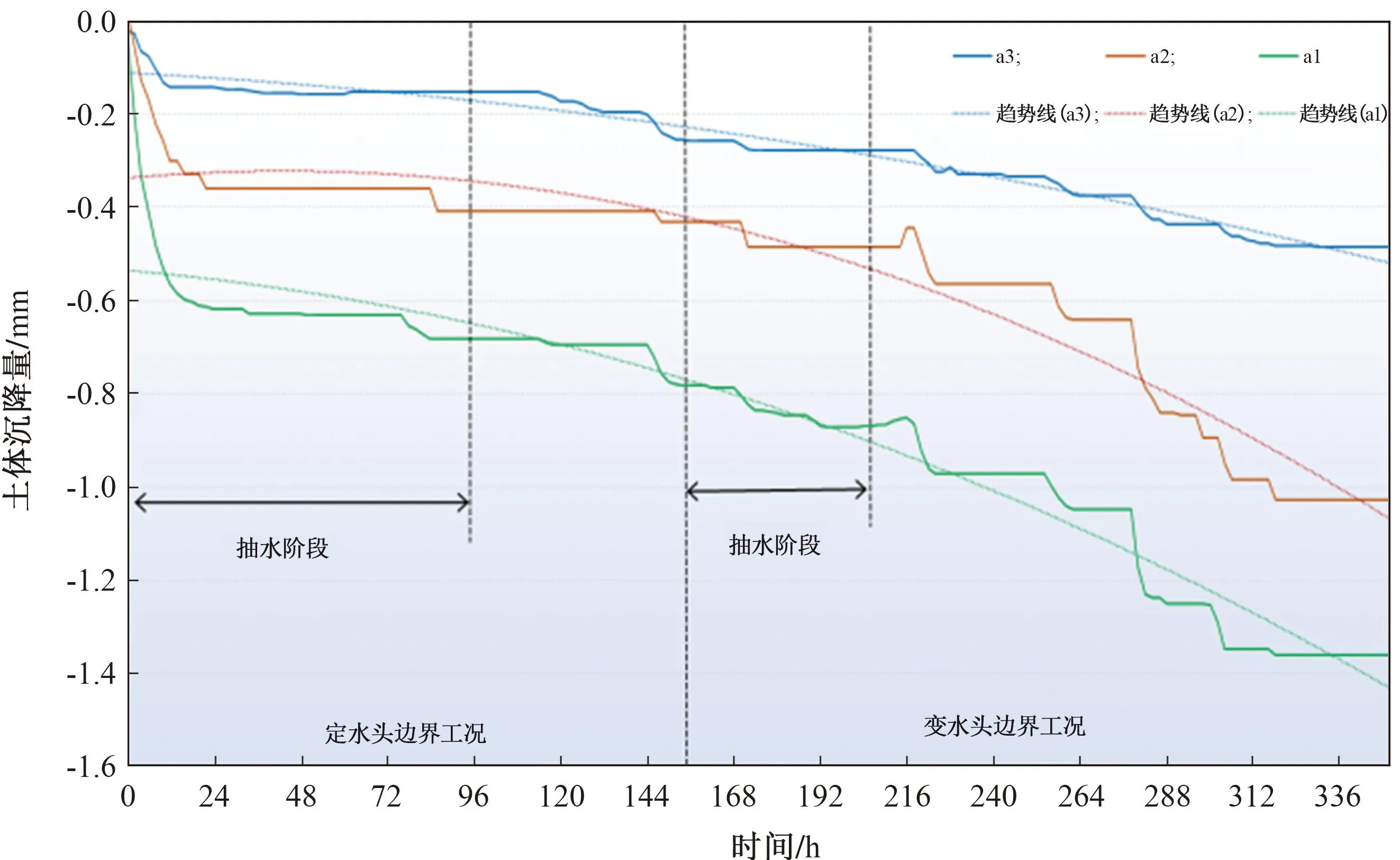
图15 第二承压含水层沉降过程线(沉降标尺)

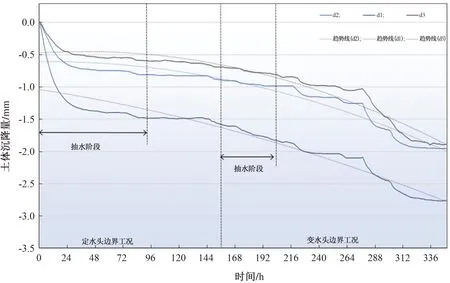
图16 第一黏土层沉降过程线(沉降标尺)

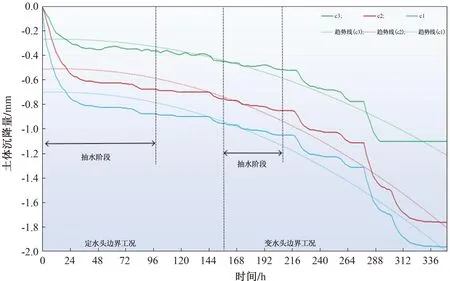
图17 第一承压含水层沉降过程线(沉降标尺)

由表2和图14—17知:

1)第二承压含水层中选取a1、a2、a3沉降标尺进行沉降分析。a1沉降标尺位于抽水井中轴线处,距左侧供水孔95 cm,定水头边界工况下,抽水后土体沉降0.682 mm,静置结束时,土体沉降0.782 mm;变水头边界工况下,抽水后土体沉降0.869 mm,静置结束时,土体沉降1.360 mm。a2沉降标尺距抽水井40 cm,距左侧供水孔55 cm,定水头边界工况下,抽水后土体沉降0.408 mm,静置结束时,土体沉降0.432 mm;变水头边界工况下,抽水后土体沉降0.486 mm,静置结束时,土体沉降1.026 mm。a3沉降标尺距抽水井90 cm,距左侧供水孔5 cm,定水头边界工况下,抽水后土体沉降0.153 mm,静置结束时,土体沉降0.256 mm;变水头边界工况下,抽水后土体沉降0.278 mm,静置结束时,土体沉降0.484 mm。

2)在定水头和变水头两种边界工况下,第二承压含水层沉降标尺a1的沉降量大于a2和a3的沉降量;第二黏土层沉降标尺b1的沉降量大于b2和b3的;第一承压含水层沉降标尺c1的沉降量大于c2和c3的;第一层黏土层沉降标尺d1的沉降量大于d2和d3的。结合沉降标尺位置可知,同一土层中沉降标尺距抽水井的距离越近,其沉降量越大,但沉降量与距抽水井的距离不成正比。在定水头边界工况下,抽水静置后各土层中各沉降标尺并没有出现抬升,但相比在抽水过程中沉降速率明显减小;在变水头边界工况下,抽水静置后,各土层中各沉降标尺沉降量持续增大,此时利用沉降标尺得到的土层内部沉降特征与利用MPS得到的土层侧面沉降特征基本一致。

2.3 讨论

2.3.1 抽水井附近沉降特征

根据MPS和沉降标尺的沉降测量数据可知,无论定水头边界工况,还是变水头边界工况,各土层在不同抽水工况下均发生波动式沉降,且存在一定的滞后性。

沉降标尺被用于测量土体内部的沉降,MPS被用于测量土体侧面的沉降。由沉降标尺和MPS测量得到的抽水井附近土层的沉降规律可知,沉降从抽水井处发生,并不断向周边扩散,传递至土体内部需要一定的时间,使得土体内部的沉降存在明显的滞后性。

2.3.2 各土层沉降特征

试验结束时各土层的沉降量如图18—21所示。

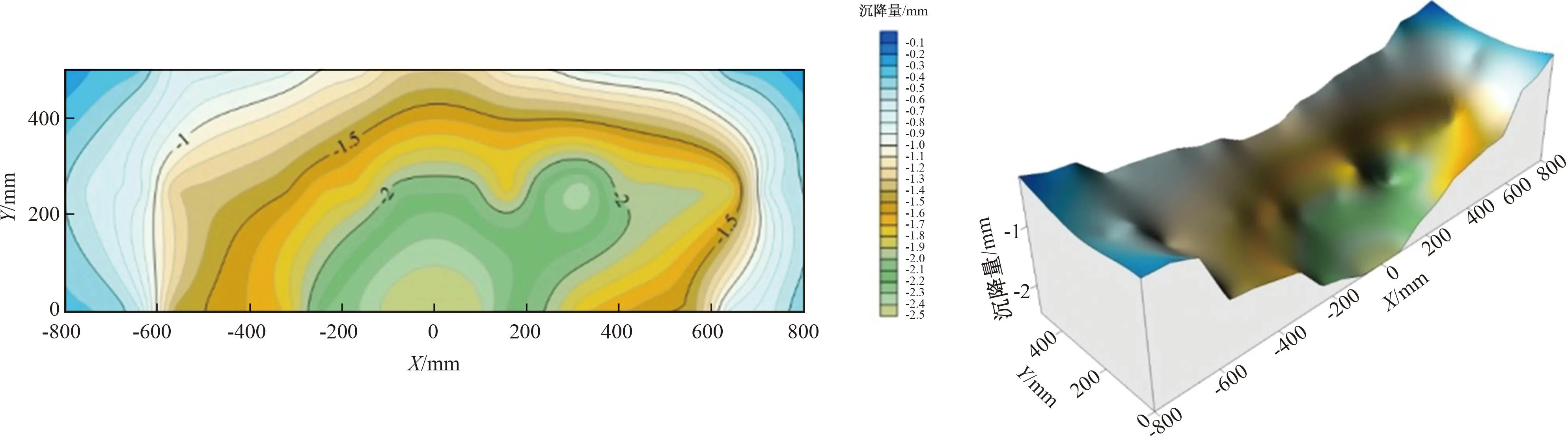
图18 第一黏土层土体沉降量

图19 第一承压含水层土体沉降量

图20 第二黏土层土体沉降量

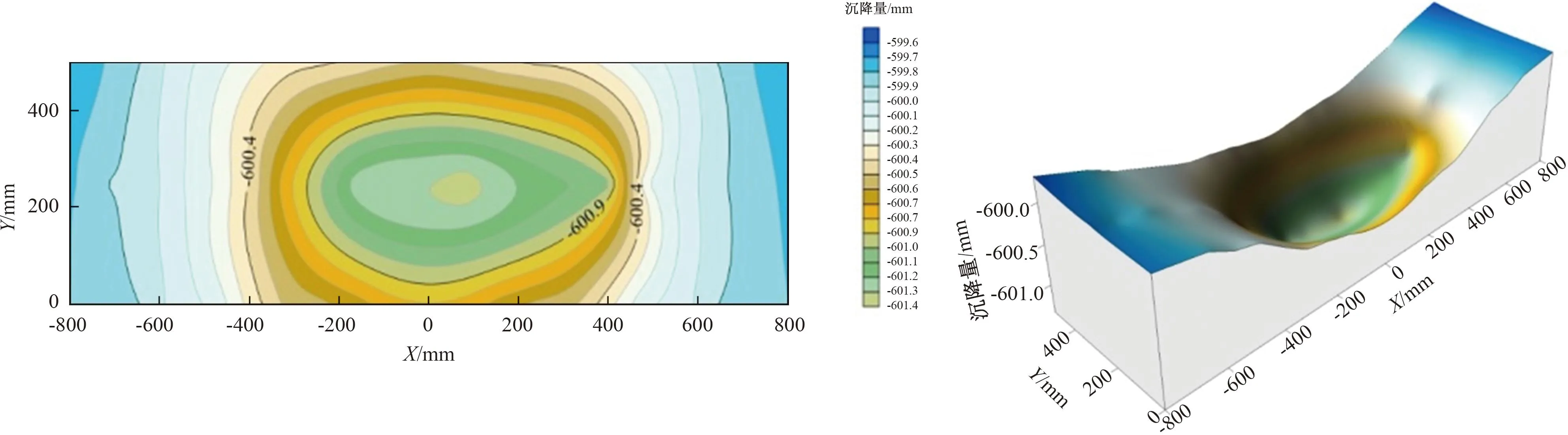
图21 第二承压含水层土体沉降量

由图18—21可知,越靠近抽水井,土体沉降量越大,越远离抽水井,土体沉降量越小,且土体沉降量下降速率与抽水井的距离呈非线性关系,各土层呈现出“尖锐凸出”的漏斗形态。对比分析黏土层与承压含水层各MPS标志点沉降量,发现抽水井附近黏土层是土体沉降量的主要贡献层。对比分析定水头边界工况和变水头边界工况沉降标尺测量数据知,变水头边界工况下的土体沉降滞后效应比定水头边界工况下的滞后效应明显,如表1和表2中沉降量增幅所示。

2.3.3 MPS标志点与沉降标尺测量数据对比

根据第二承压含水层土体沉降测量数据,在距供水井孔较近的MPS标志点A3、A19处的土体沉降量呈小幅上升的趋势,而距供水井孔较近的沉降标尺a3处的土体沉降量呈缓慢下降趋势。两种设备的沉降测量结果存在明显差异的主要原因为:沉降标尺a3自身质量较大,周边水体的上浮力小于沉降标尺的自身重量,使得沉降标尺a3处的土体沉降曲线呈缓慢下降趋势;而MPS标志自身质量轻,自身重量远小于水体上浮力,能更准确获取土体变形量。综合第二黏土层、第一承压含水层和第一黏土层土体沉降测量数据,距抽水井位置大致相同的沉降标尺与MPS标志点处的土体沉降变化趋势一致,土体沉降量接近。对比分析可知,数字近景工业测量不仅可用于流固体的变形测量,能测出地下水位波动条件下土体变形的瞬时变化过程,具有较高的灵敏度。

3 结论

1)定水头边界工况下,距抽水井距离增大,各土层沉降量明显减小,抽水静置后,各土层沉降有不同程度的回弹;变水头边界工况下,抽水静置后,各土层沉降量持续增大。变水头边界工况下的土层沉降滞后效应比定水头边界工况下的更明显,漏斗形态也更加突出。

2)对比沉降标尺和MPS标志点的沉降监测数据可知,在定水头边界工况下,由于标志点相对沉降标尺较轻,测量数据能较好地反映地下水位波动工况下土体变形的瞬时特征;在变水头边界工况下,这两种测量方法所测得的数据反映的土层沉降特征基本一致,说明MPS工业摄影测量可用于监测土体变形。

受试验环境影响,此次试验采用 MPS/S单相机摄影测量,无法做到实时采集沉降数据,后续研究可采用MPS/M多相机摄影测量建立多机位拍摄系统,开展实时动态沉降监测。