深圳市极端降水时空演变特征分析
王俊阳, 史海匀
(1.深圳市城市环境健康风险精准测量与预警技术重点实验室,广东 深圳 518055; 2.南方科技大学 环境科学与工程学院,广东 深圳 518055)
随着科技发展以及人口数量的不断增长,全球气温的上升速率在不断增大,联合国政府间气候变化专门委员会(Intergovernmental Panel on Climate Change,IPCC)第六次评估报告显示,依据未来20年的平均温度变化情况进行预估,全球气温上升将达到或超过1.5 ℃,超出历史同期水平。全球气温的不断上升将造成气候变化加剧,致使干旱、强降水、高温热浪等极端气候事件频发。近年来,全球多数地区极端降水事件发生频率显著增加,降水量时空分布呈现不确定性,洪涝灾害表现出更加频繁的趋势,严重影响生态系统稳定和人民生命财产安全[1-3]。因此,针对极端降水的一系列研究具有重要意义。
国内外学者从不同方面开展极端降水事件的研究,并取得了一系列成果,为多地气象灾害预防提供了参考。NIE Y B等[4]研究了雨季时中国西南地区低纬度季内浮动对持续极端降水事件的影响机制发现,西南地区上空的持续极端降水事件由西北太平洋上空具有几乎相反相位的两种不同类型的7~20 d Rossby波预调节,这两种Rossby波分别对西南地区两种类型的持续极端降水事件有直接和间接的影响;HENNY L等[5]依据不同影响因素对极端降水的影响占比划分出了大西洋中部和美国东北部的极端降水天,发现极端降水天的季节性降水量均呈增加趋势,冬季和春季极端降水天的降水量强度和频次均增加,这一结果主要是由大气环流造成,而在夏秋季极端降水天的降水量频次发生增加则是由于热带气旋、大气环流以及极端综合水汽输送等因素影响产生;HU W F等[6]探讨了青藏高原与其周边地区的极端降水的周期性和变化趋势以及与海洋涛动因子之间的关系发现,在研究区域中极端降水总体呈上升趋势且表现出明显的时空分布差异,在研究时段内,各个极端降水指数表现出不同的振荡周期,同时发现海面温度指数与极端降水指数的振荡周期相近且海温指数与极端降水指数有强相关性,海温异常现象先于极端降水事件发生;高延康等[7]依据单一元统计极值分布法和混合元统计极值分布法对1961—2020年逐日降水栅格数据进行处理,得出台风对高阈值的极端降水影响较大,其引起的极端降水占比从沿海地区到内陆地区逐渐下降,同时发现考虑台风引起的降水有助于提升大部分地区的极端降水概率估计准确性。
深圳市作为我国全国性经济中心城市之一,极端降水是其主要灾害性天气之一。短时强降水发生时易出现系统性对流云团,同时引起突发洪水等现象,进而造成深圳市航班不同程度的延误、户外工作停工停产、交通受阻、人员伤亡和财产损失等后果,严重影响深圳市社会经济持续稳定发展。我国学者对深圳市的降水事件进行了较多研究,史贵君等[8]通过对深圳市降水相对变化率、降水集中度和集中期等指标进行计算,采用Mann-Kendall趋势分析方法等对计算结果进行分析发现,深圳市年内降水分布稳定性较差,降水分配逐渐平均,年际降水分配较不稳定但其分布逐渐稳定;SHAO W W等[9]依据1953—2020年深圳站实测降水数据计算了深圳市的年降水量和月降水量,发现深圳市月均降水量为160.8 mm,最大月降水量为1 395.3 mm,深圳站在4—9月的降水量占年降水量的85.11%;卢晓雄等[10]基于深圳市2008—2017年自动气象站小时降水数据进行分析,得到深圳市降水量呈现东部多、西部少的分布特点,大多数行政区降水量均存在不显著上升趋势,全部站点的降水日数均呈微弱上升趋势,年内降水集中度较强且各月降水变化程度不同;LIU Y Y等[11]基于机器学习和数值天气预报等方法提出了一种可以依据未来气压场、风场等数据准确预测由热带气旋引起的降水的新方法,并利用深圳市自动气象站收集的降水数据验证了该方法的可靠性,进一步提升了深圳市降雨量预测的准确性。
综上,国内外学者对极端降水的研究较为丰富,多集中于不同时间或空间尺度下极端降水的特征、影响因素及机理等方面,可从多角度为城市建设及灾害预防提供指导性参考。然而,受城市发展水平及地理环境特征等因素的影响,极端降水在不同地区的表现具有一定的区域性特征[12-13]。其中,针对深圳市的研究多从降水的年内年际分配、空间分布等方面展开,有利于了解深圳市的整体降水状况以及水资源空间分布格局,但涉及极端降水的研究目前相对有限,不利于防控洪涝灾害。针对以上局限性,本文从深圳市极端降水的空间分布、演变趋势以及周期变化等方面探究深圳市极端降水的时空演变特征,以期识别深圳市的极端降水高风险区,并揭示极端降水的演变规律,为深圳市暴雨风险评估以及城市建设规划提供重要参考。
1 研究区概况
深圳市隶属于广东省,位于我国南部沿海地区,珠江口东岸,位于东经113°43′~114°38′,北纬22°24′~22°52′。深圳市所处纬度较低,属于亚热带向热带过渡型海洋性气候,气候温和,日照充足,汛期持续时间长,降水丰富,年均降水量为1 935.8 mm[14],各月降水呈双峰型分布,6月和8月各有一个峰值,暴雨是其最主要的气象灾害之一,自20世纪90年代以来暴雨日数显著增加,近10年的年平均局部地区发生暴雨日数达48.3 d[15-16]。
深圳市东西狭长,地形分布较为复杂,地势东南高、西北低,占地面积为1 997.47 km2,共包含宝安区、福田区、南山区等9个行政区和大鹏新区1个功能区[17],如图1(a)所示。2004年深圳市率先达到全面城市化[18-19],是全国性的经济中心城市和国际化大都市。近几十年来深圳市城市化发展迅速,引发局部地区气象要素剧烈变化,市内降水分布不均,造成局部地区强降水及内涝突发,严重影响人们日常生活及社会经济可持续发展[10]。发生于2023年9月7日的“9·7特大暴雨”具有“强度超大、持续时间长、强降雨范围广”等特征,打破了深圳市自1952年以来六项历史极值,从当日下午17时至次日上午6时共13 h的平均降水量为202.8 mm,最大累计降水量达469.0 mm,造成全市多地严重内涝,经济损失惨重。
2 数据来源与方法
2.1 数据来源
本文采用的降水资料来源于国家青藏高原科学数据中心的中国区域地面气象要素驱动数据集(1979—2018年)。该数据集包含了深圳市降水、风速、长波辐射等7个气象要素,是以国际上现有的Princeton再分析资料、全球陆面数据同化系统(Global Land Data Assimilation System, GLDAS)资料、全球能量与水循环试验-地表能量收支(Global Energy and Water Exchanges Project-Surface Radiation Budget, GEWEX-SRB)辐射资料以及热带降水观测计划卫星(Tropical Rainfall Measuring Mission Satellite, TRMM)降水资料为背景场,融合了中国气象局常规气象观测数据制作而成,可用于水文建模、地表建模、陆地数据同化以及其他陆地建模,数据集的时间分辨率为3 h,水平空间分辨率为0.1°[20-21]。降水资料涵盖深圳市全域面积的栅格点共计34个,为便于后续描述,本文按照从上至下、从左至右的顺序对栅格点进行编号,如图1所示。
2.2 研究方法
本文选用世界气象组织推荐的包含绝对指数、相对指数等在内的9个极端降水指标[22-23](表1),分析极端降水事件的空间变化特征。此外,采用滑动平均法、Mann-Kendall趋势分析法、Sen′s坡度法等方法,从降水量、降水强度、暴雨日数等角度,全面分析深圳市极端降水的时间演变趋势,采用小波分析法分析深圳市极端降水的变化周期。
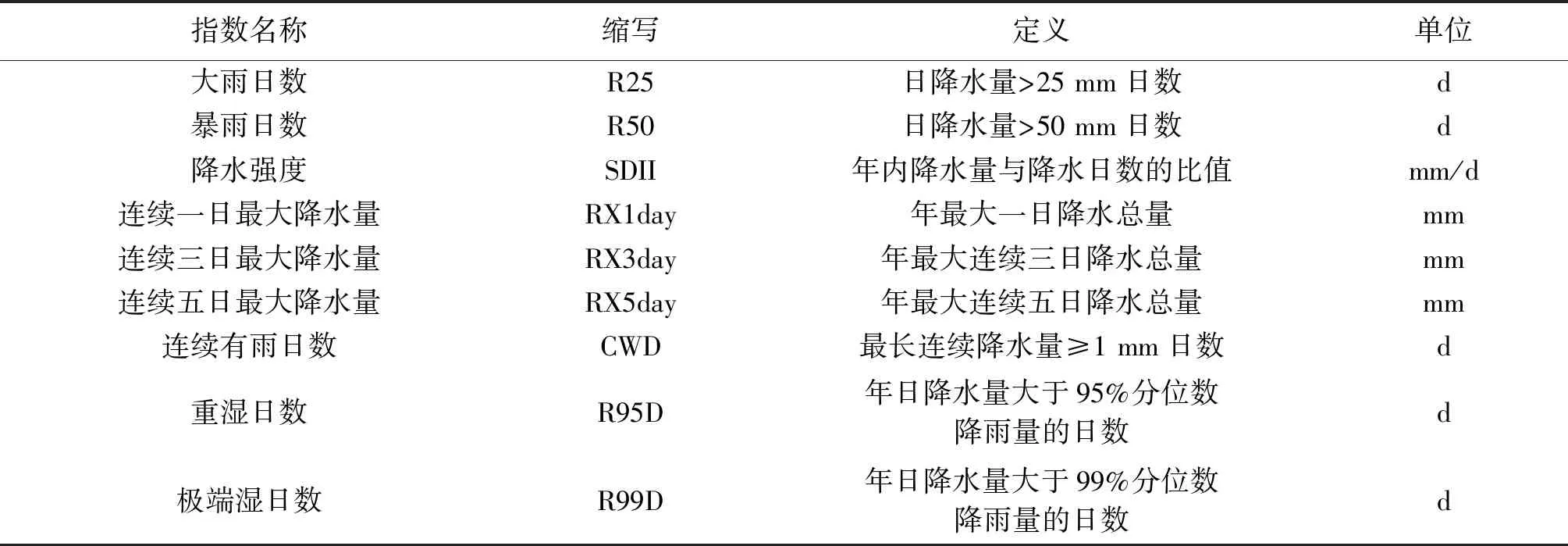
表1 极端降水指标名称及定义
2.2.1 Mann-Kendall趋势分析法
Mann-Kendall趋势检验法是一种在气象学、水文学等学科中常用的一种分析时间序列数据变化趋势的方法,该方法不要求样本符合正态分布,同时该方法对异常值不敏感,常被用于分析降水、温度等指标的时间序列变化趋势[24-26],其计算方法如下:
1)在给定的时间中,变量关于时间的平稳独立且连续分布的序列为X={x1,x2,…,xn},统计量S的计算公式为:
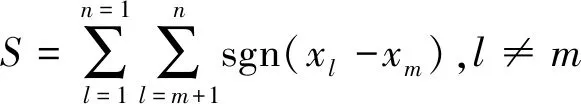
(1)
(2)
式中:n为样本数;m和l均为小于样本总个数n的非等值阿拉伯数字;xm、xl均为变量;S为统计量。
2)S的方差计算如下(当样本数n≥10时,认为统计量S近似服从正态分布):
(3)
式中Var(S)为统计量S的方差。
3)Mann-Kendall统计量Z的计算公式如下:
(4)
统计量Z用来表示变化趋势的强度。当统计量Z>0时,指标在该时间序列上为增长趋势,相反则为减小趋势。当统计量Z的绝对值大于1.96时,表明时间序列的增长趋势或减小趋势显著。
2.2.2 Sen′s坡度法
Sen′s坡度法是一种非参数的趋势斜率计算方法,不受序列奇异值的影响,可以很好地反映时间序列趋势的变化程度,是对Mann-Kendall趋势检验法的补充,两者结合使用可以更好地计算时间序列的变化率[27-28]。
变量关于时间的独立分布且连续的序列为X={x1,x2,…,xr},Sen′s坡度法估计趋势度Y的计算公式如下:
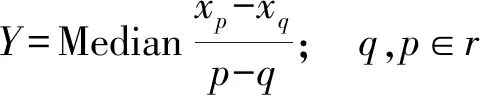
(5)
式中:r为样本数;q和p均为小于样本总个数r的非等值阿拉伯数字;xq、xp均为变量。趋势度Y常用来判断时间序列趋势的升降,当Y>0时,时间序列呈上升的趋势,反之呈下降的趋势。
2.2.3 小波分析法
小波分析是对傅里叶变换的发展延伸,相较于傅里叶变换,小波变换通过伸缩和平移变换可以在时域和频域上独立地对信号进行处理和表达,具有很好的局部化特性,其可以充分反映连续性变量序列的变化趋势,揭示事件序列的多种变化周期[29-31]。小波变换常见形式为连续小波变换和离散小波变换,本文采用其中的连续小波变换方法开展对降水量的多尺度分析,以期了解其周期性特征。
连续小波变换是小波变换最基本的形式。给定一个原始连续信号E(t),连续小波变换通过将E(t)与一个基本小波函数ψ(t)进行卷积得到一组连续小波系数:
(6)
式中:CWT(u,w)表示在给定尺度u和位置w下的小波系数[32-33];ψ*(t)为ψ(t)的复共轭函数。
3 结果分析
3.1 深圳市极端降水空间分布特征分析
本文计算了9个极端降水指标40年的平均值,并以此作为每个栅格点的极端降水指标值,分析深圳市极端降水指标的空间分布特征,如图2所示。

图2 深圳市极端降水指标的空间分布(1979—2018年)
由图2可知,1979—2018年深圳市极端降水指标的空间分布为:南部的大雨日数(R25)和暴雨日数(R50)高于北部;降水强度(SDII)整体呈从东南向西北方向递减的趋势;连续一日最大降水量(RX1day)、连续三日最大降水量(RX3day)以及连续五日最大降水量(RX5day)均呈南部高于北部分布,其中东南方向的南山区、福田区、罗湖区所在区域的值最大;连续有雨日数(CWD)在北部以及东南方向的值较大,福田和罗湖区所在区域的值最小;重湿日数(R95D)呈西部多于东部分布;极端湿日数(R99D)则为西部和中部多于东部。整体上,深圳市南部极端降水的发生频率及强度大于北部,中南部降水日的连续性较弱,而相较于东部,深圳市西部地区降水资源更为丰富。
使用Sen′s坡度法以及Mann-Kendall趋势分析法计算每个栅格点极端降水指标时间序列的平均变化率,进而分析深圳市极端降水指标变化趋势的空间分布特征,如图3所示。
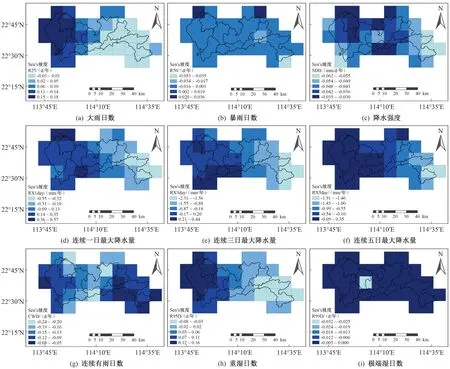
图3 深圳市极端降水指标变化趋势的空间分布(1979—2018年)
由Mann-Kendall趋势检验法计算结果和图3可知:40年来深圳市大雨日数(R25)整体呈上升趋势,西部上升趋势大于东部,且西部呈显著上升趋势,而东部上升趋势并不显著,大体呈稳定或较小趋势;对于暴雨日数(R50)变化,西部呈稳定状态,东部呈稳定和非显著性下降趋势;降水强度(SDII)各栅格点呈不同程度的显著性下降趋势;连续一日最大降水量(RX1day)、连续三日最大降水量(RX3day)以及连续五日最大降水量(RX5day)均为西部呈上升趋势,东部呈下降趋势,但其变化趋势并不显著;连续有雨日数(CWD)在东西部呈不显著下降趋势,中部呈显著性下降趋势;重湿日数(R95D)除东部小部分地区呈非显著性下降外,整体呈非显著性上升趋势;极端湿日数(R99D)整体呈稳定状态。综上,随着年份的增加,深圳市在极端降水日数及极端降水量两方面整体呈现非显著性的上升趋势,且西部上升速率高于东部,而连续有雨日数整体呈现下降趋势,东西两部下降频率低于中部地区的。
3.2 深圳市极端降水多发区的分布
为更好预测未来暴雨,提前预防洪涝灾害的发生,在对极端降水指标进行计算的基础上,本文又从降水量以及降水强度两方面对降水数据进行了计算分析,以期识别深圳市的极端降水频发地区。
3.2.1 极端降水量
本文分别计算了深圳市每年连续一日降水量排前五的降水量值、每年连续三日降雨量排前五的降水量值、每年连续五日降雨量排前五的降水量值,并统计这些值所在栅格点的位置,计算40年间这些值位于各栅格点的总频次,最后将各栅格点划分为不同等级的风险区(风险区划分依据:将总频次数值按照从小到大原则进行排列,除0以外,其余数值以5为区间平均分为四个区间,总频次数值位于这四个区间的栅格点分别划分为低、中、高及极高风险区;总频次为0的栅格点划分为无风险区),展现深圳市不同区域的暴雨发生风险。考虑到极端降水偶然事件的发生,本文同时计算了40年中每个时间段(将40年均分为8个时间段)的每年排前五的降水量值位于各个栅格点的总频次,并找出总频次最大值所在栅格点,分析最大值栅格点随时间段的变化,结果如图4和图5所示。
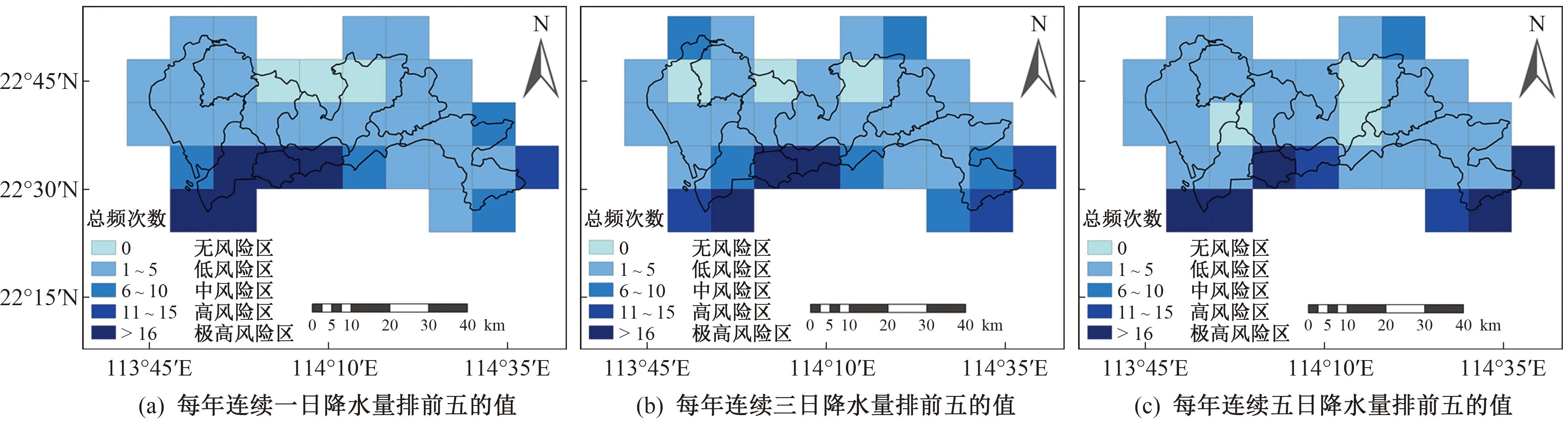
图4 每年连续降水量排前五的值在各栅格点40年的总频次分布
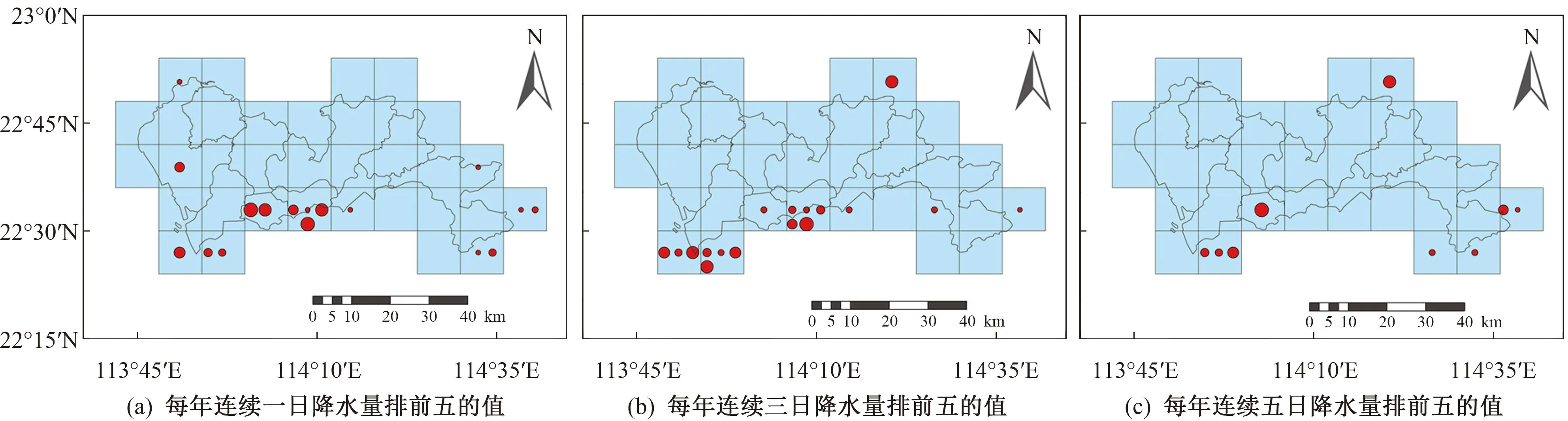
图5 各时间段每年连续降水量排前五的值的累积频次最高栅格点分布(1~8个时间段的最高频次栅格点由圆点从小到大表示)
1979—2018年,深圳市大部分区域处于低风险区,仅个别栅格点所在区域处于极高风险区、高风险区和无风险区,栅格点P7、P11、P12、P15、P18、P33、P34处频次最高,是极端降水发生的极高风险区;在8个时间段的发展过程中,深圳市极端降水多发地区的分布整体呈从分散到集中的变化趋势,表现出从栅格点P3、P15、P18、P29、P33、P34向栅格点P7、P12、P15、P18、P23迁移的趋势,强降水在各时间段多发生在栅格点P7、P12、P15、P18处。综合考虑,未来极端降水在栅格点P7、P12、P15、P18处发生的可能性较大。
3.2.2 极端降水强度
暴雨一般指每小时降雨量达16 mm以上、连续12 h降雨量达30 mm以上或连续24 h降雨量达50 mm以上的降水。为更准确地分析深圳市极端降水的分布情况,本文分别计算每个栅格点的不同历时(1 h、12 h、24 h)的滑动降雨量,并判定其是否达到暴雨标准。统计每年暴雨发生次数以及40年来暴雨发生总频次在所有栅格点的占比,考虑到极端降水偶然事件的发生,本文同时计算了每个栅格点每个时间段(将40年均分为8个时间段)暴雨发生的总频次,并分析最大值所在栅格点的变化过程,结果如图6和图7所示。

图6 各栅格点暴雨发生总频次占比分布
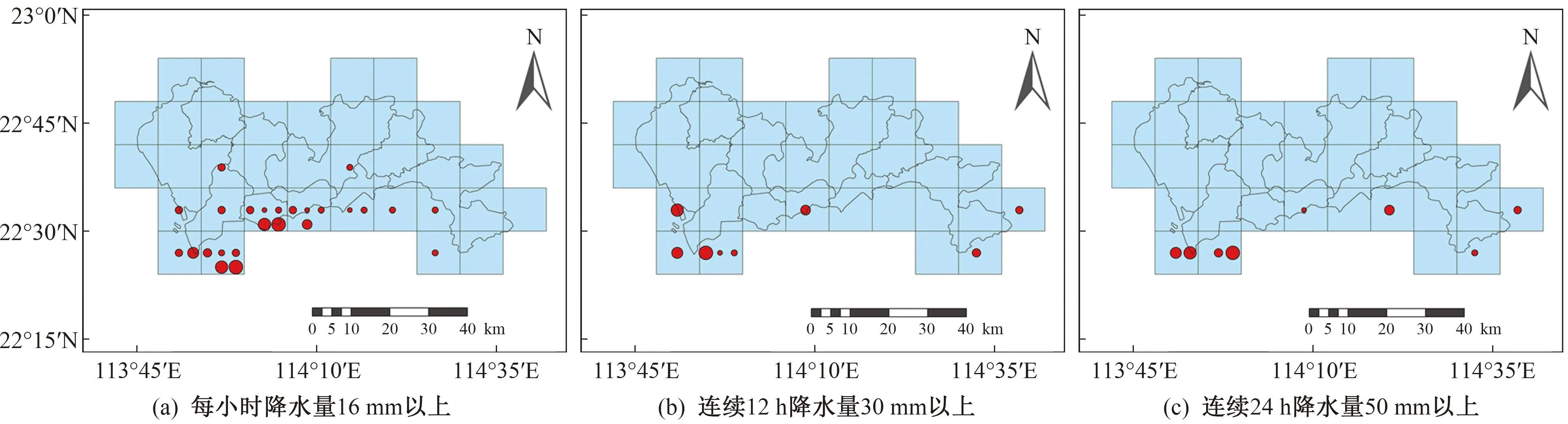
图7 各时间段暴雨发生最高频次栅格点分布(1—8个时间段的最高频次栅格点由圆点从小到大表示)
1979—2018年深圳市北部的暴雨发生频次低于南部,发生暴雨的风险相对较小,南部栅格点P7、P11、P12、P15、P18、P22、P30、P33处在所有栅格点中发生暴雨频率较高,是暴雨发生高风险区域;分8个时间段进行分析,暴雨在栅格点P7、P12、P15、P18处较为稳定,此外,暴雨还呈现从栅格点P12、P15、P18、P22、P26、P29、P33、P34向栅格点P7、P12、P15、P18迁移的趋势。综合考虑,极端降水在栅格点P7、P12、P15、P18处发生的频率较高。
3.3 深圳市极端降水时间变化特征分析
基于以上从不同方面对深圳市极端降水空间分布的分析可知,栅格点P7、P12、P15和P18处的极端降水事件发生频率最高。由于栅格点P7和P12所涵盖的深圳市地域面积较少,因此本文仅选取栅格点P15和P18(分别包含福田区和罗湖区大部分地域)作为代表性研究区域,分析深圳市极端降水时间变化特征。
3.3.1 年内变化特征
分别计算1979—2018年深圳市每个月的暴雨日数以及最大日降水量,进一步分析其在每个年代的月变化特征。图8为两个栅格点在20世纪80年代、90年代和21世纪00年代、10年代(图中用1980s,1990s,2000s,2010s进行标注)的月均暴雨日数以及月最大日降水量的月变化趋势图。
由图8可知:两个栅格点在4个年代的月均暴雨日数变化曲线均随时间呈上升趋势,其中20世纪90年代的上升趋势最为明显;栅格点P15的月最大日降水量变化曲线除21世纪10年代呈下降趋势外,其他3个年代的均呈上升趋势,其中20世纪90年代的上升趋势最为明显,栅格点P18的4个年代月最大日降水量变化曲线均呈上升趋势,最为明显的为20世纪90年代的;此外,栅格点P15和P18的月平均暴雨日数变化曲线均呈双峰型,月最大日降水量变化曲线均有三个峰,其中一个主峰,另外两个均为小峰,但在不同年代,峰的起始时间和大小各不相同,峰值主要集中在每年的6、7、8三个月。
3.3.2 年际变化特征
1979—2018年栅格点P15和P18的年降水量及5年滑动平均降水量的变化曲线如图9所示。栅格点P15和P18的年降水量年际变化趋势基本一致,整体呈波动性下降趋势,根据Mann-Kendall趋势检验法计算得出两个栅格点的Z值分别为-0.489和-0.885,因此其下降趋势并不显著。栅格点P15和P18近40年的年平均降水量分别为1 926.35 mm和1 895.12 mm,略低于深圳市多年平均降水量。P15和P18栅格点的年降水量的极值波动较为频繁且变化幅度较大,其中2008年以及2016年的降水量变化最大,分别超出临近年份1 000 mm左右,而降水量最大值主要分布在2001年和2008年,降水量均在2 600 mm以上,最小降水量则主要发生于1991、2004以及2011年,降水量均在1 200 mm左右。

图9 1979—2018年栅格点P15和P18年降水量及5年滑动平均降水量变化曲线
P15和P18栅格点的年降水量小波分析如图10所示。由图10可知,1979—2018年中栅格点P15和P18年降水量均存在两个周期性振荡,栅格点P15年降水量在20世纪90年代初期至21世纪00年代中期存在显著的6~8年振荡周期,在21世纪00年代中期至21世纪00年代末期存在1~2年的振荡周期;栅格点P18年降水量在20世纪90年代初期至21世纪00年代初期存在显著的7~8年振荡周期,在21世纪00年代中期至21世纪00年代末期存在1~2年的振荡周期;栅格点P15和P18年降水量振荡周期均以长时间尺度振荡周期最为显著。
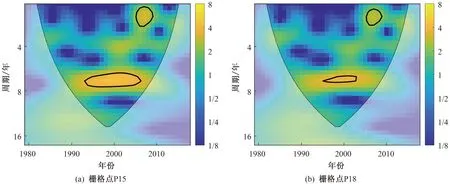
图10 1979—2018年栅格点P15和P18年降水量小波分析
根据深圳市的气候特征,将四季划分如下:春季3—5月,夏季6—8月,秋季9—11月,冬季当年12月—次年2月。图11为两个栅格点P15和P18 40年来的春、夏、秋、冬四个季节降水量(采用“邻近”年份添补方法,2018年冬季降水量的1、2月降水量用当年的1、2月降水量代替计算)的年变化曲线,可知季节降水量整体呈现夏季>春季>秋季>冬季的分布趋势。对P15和P18两个栅格点的季节降水量进行趋势检验,结果见表2。P15和P18两栅格点的春季降水量均呈不显著下降趋势,冬季降水量均呈不显著上升趋势,栅格点P15的夏季和秋季降水量均呈不显著上升趋势,而栅格点P18的夏季和秋季降水量均呈不显著下降趋势。

表2 栅格点P15、P18的季节降水量趋势检验值
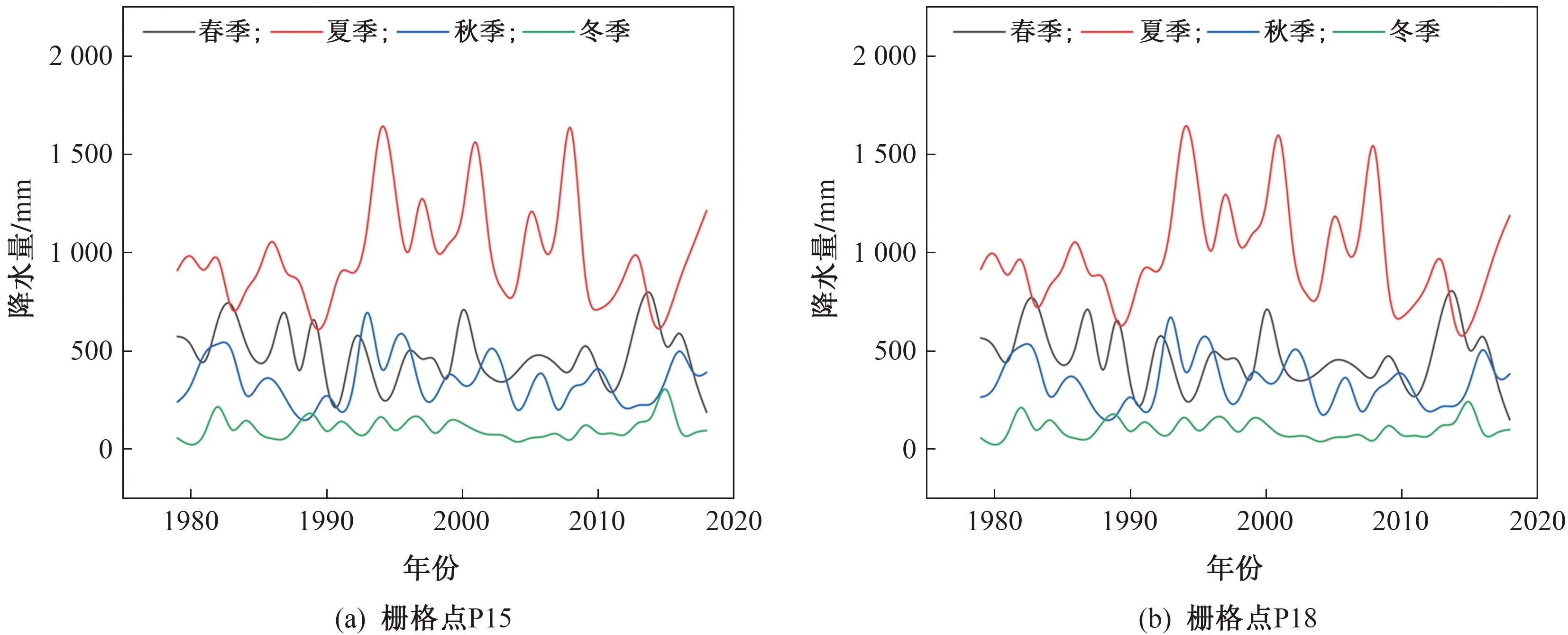
图11 1979—2018年栅格点P15和P18的季节降水量年变化曲线
图12为P15和P18两个栅格点的季节降水量的小波分析图。由图12可知:栅格点P15的春季降水量在20世纪80年代末期至20世纪90年代中期存在1~4年的显著性振荡周期,栅格点P18春季降水量在20世纪80年代末期至20世纪90年代末期存在2~5年的显著性振荡周期;在21世纪00年代两栅格点的夏季降水量存在振荡周期,栅格点P15存在1~4年的显著性振荡周期,栅格点P18前后存在6~7年的振荡周期,此外,在21世纪10年代存在6~7年的振荡周期(未通过可信度检验);栅格点P15秋季降水量在20世纪80年代中期至20世纪90年代分别存在9~13年的振荡周期(未通过可信度检验)、1~4年的显著性振荡周期,栅格点P18秋季降水量在20世纪90年代、21世纪00年代初期至中期分别存在2~4年、3~4年的显著性振荡周期;两栅格点的冬季降水量在近40年的时间序列中均不存在明显振荡周期。
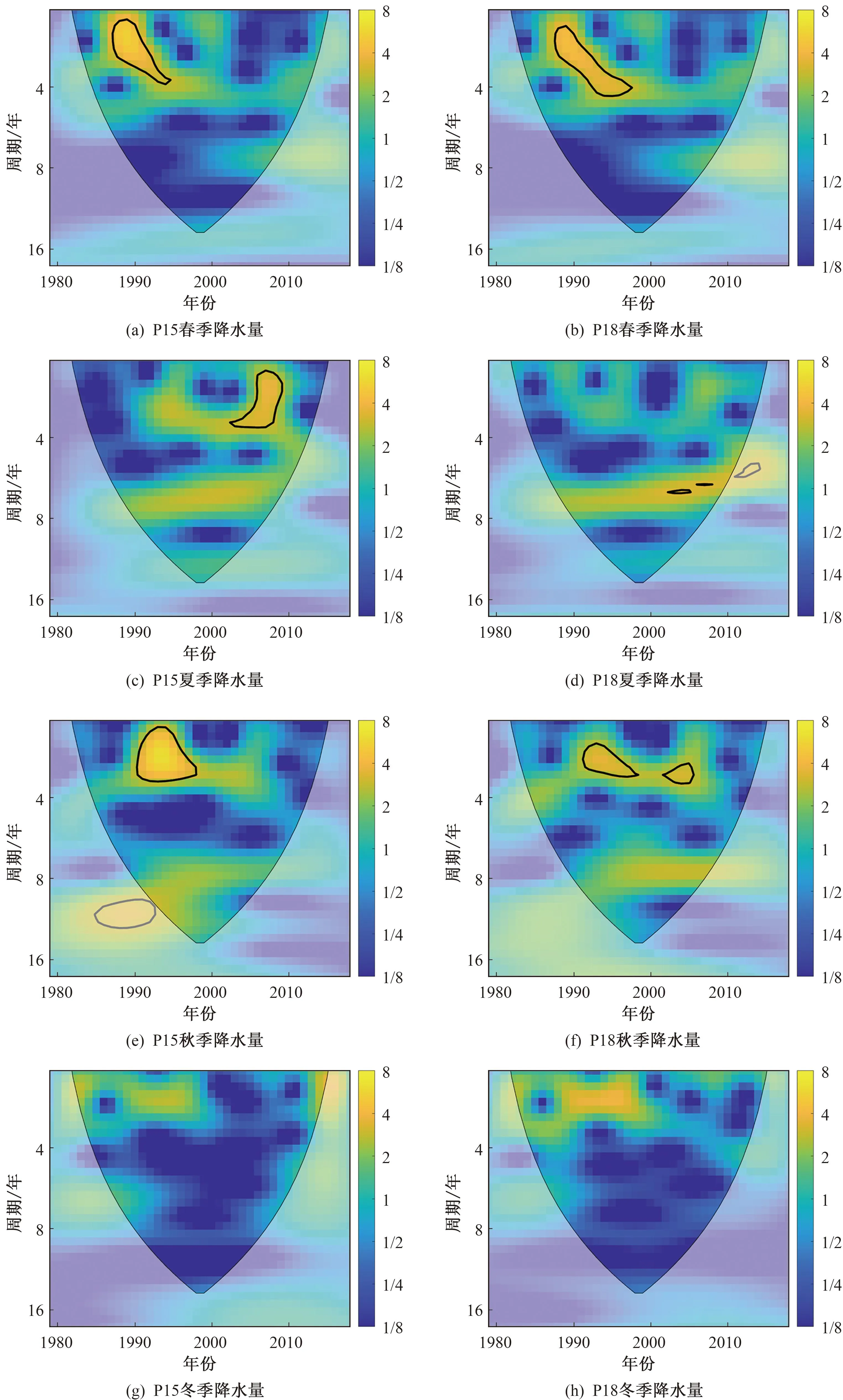
图12 1979—2018年栅格点P15和P18的季节降水量小波分析
分别统计栅格点P15和P18的年暴雨日数,同时计算每年的最大日降水量,分析其随时间的变化。图13为栅格点P15和P18的年暴雨日数以及年最大日降水量的线性趋势。由图13可知,P15和P18两个栅格点的年暴雨日数均呈先上升后下降的变化趋势,整体呈下降趋势但下降趋势并不显著。根据Mann-Kendall检验法计算得出两个栅格点的Z值分别为-0.361和-0.722。P15和P18两栅格点的年暴雨日数为3.00~19.00 d,平均分别为7.93 d和8.00 d,最大值均出现在2001年,分别为17.00 d和19.00 d,栅格点P15在1988年和2004年的年暴雨日数最少,栅格点P18在1988年的年暴雨日数最少,均只有3.00 d;P15和P18两个栅格点的年最大日降水量变化均呈波动性上升趋势,由于其Z值分别为0.618和0.361,其上升趋势并不显著,在1994年,两栅格点的年最大日降水量均为近40年中最大值,分别为264.18 mm和258.42 mm,近40年中最小值出现在1991年,分别为69.00 mm和70.68 mm,极差较大,在190.00 mm左右。
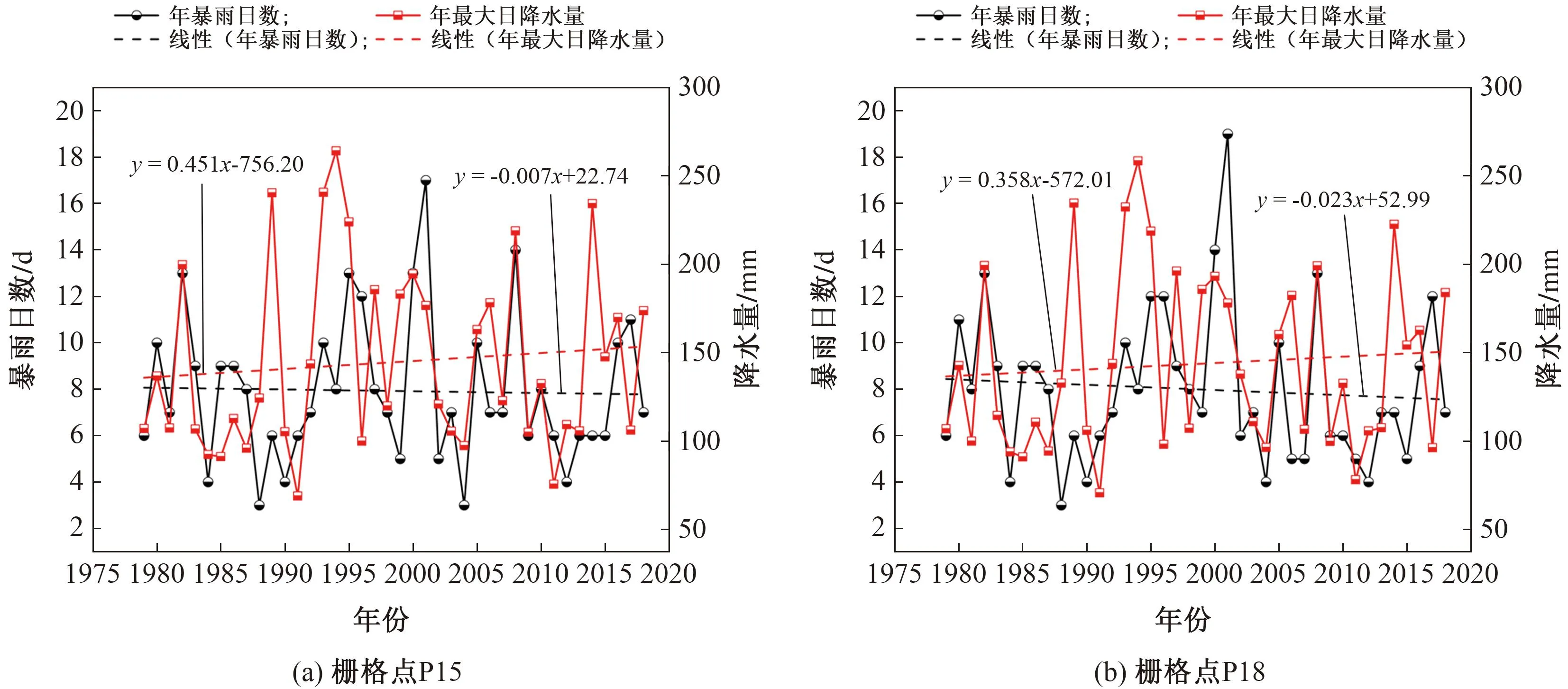
图13 1979—2018年栅格点P15和P18的年暴雨日数以及年最大日降水量变化曲线
4 讨论
本文在分析极端降水指标的时空分布时,发现深圳市1979—2018年R25、R50、RX1day、RX3day、RX5day、R95D以及R99D等极端降水指标均呈现西南方向较高、东南方向次之、整体向北方逐渐减小的分布规律,这一分布规律符合降水从沿海地区到内陆逐渐减少的特征,但同时这些极端降水指标在研究时间范围内在东部的下降趋势大于西部,上升趋势小于西部,即深圳市东部的极端降水频次呈减小趋势,而西部呈增加趋势。此外,深圳市极端降水高风险区呈现从东南部城市边缘大鹏新区向西南方向和中部的南山区小部以及福田、罗湖区大部等城市中心迁移的趋势,即极端降水的发生地区从深圳市的城市边缘向中心迁移,这一趋势与深圳市的城市中心变化相一致。目前,已有大部分研究[34-37]发现城市化对降水的影响作用逐渐加强,可通过多种方式促进极端降水的发生,造成极端降水事件明显增加。作为我国改革开放的先行者,40余年来深圳市乃至整个珠江三角洲地区经济快速发展,城市化进程遥遥领先,其极端降水的发生受到较大影响,其极端降水中心的变化在一定程度上是由快速城市化引起的。发生这一迁移现象的原因多为城市边缘的热带气旋、海洋水汽等更易引起极端降水[38],随着城市化的不断发展,城市密集的建筑物使风速减小,强雨带等天气系统在城市上空区域滞留的时间变长,引起区域降水特征的变化,进而易造成极端降水的发生[39-41]。
力梅等[42]发现,深圳市的短时强降水重点防范区主要为宝安区、大鹏新区、龙华新区南部,以及福田、罗湖区和光明新区的小部分区域,这与本文结果有一定的差别。本文采用的是近40年长期栅格降水数据,而力梅等[42]的研究结果则是基于106个气象站5年(2008—2012年)逐分钟雨量数据计算得到。考虑到栅格数据和气象站数据的差异性以及不同研究年限期间的各种影响因素,关于极端降水高风险区的确定还需采用更加完善的数据进行进一步计算验证。
本文在分析深圳市极端降水频发地区的降水年内变化特征时发现,相较于其他三个年代,在20世纪90年代月暴雨天数和最大日降水量随月份的增加上升幅度最大,结合图8分析发现,在这一年代深圳市的雨季发生了滞后及高强度降水。自从20世纪70年代末之后,华南地区城市化进程不断推进,在20世纪90年代,经济处于快速发展期,同时也是污染较为严重的时期,下垫面条件剧烈改变、大气中PM2.5等颗粒物不断增多,进而造成空气中有大量的凝结核,形成城市雨岛效应,局部的区域降水特征被改变。结合李书严等[43-45]对北京等地短时强降水分布特征的研究推测这一时期的降水环境污染状况可能使得极端降水事件的发生概率增加,同时也可能引起深圳市这一年代年内暴雨事件发生的时间后移以及降水的波动增大,进而使得极端降水在年内呈较大幅度的上升趋势。在进入20世纪00年代以后,随着环境保护认知的增强,环境治理工作开始实施,雾霾等污染现象减少,降水的波动相应减小。此外,在这一年代,太平洋10年涛动(PDO)相变发生较为频繁和剧烈,而PDO能在很大程度上影响极端降水变化,因此这也可能是这一年代雨季后移的原因之一[46-48]。
本文发现深圳市极端降水频发地区的年降水量变化趋势呈不显著下降趋势且存在1~2年和6~8年的振荡周期,而丁楠等[49-50]的研究发现深圳市的站点年降水量呈微弱上升趋势,且存在5~7年、17~20年和11年左右的振荡周期。本文研究的深圳市部分区域,而丁楠等[49-50]研究的是深圳市全域,其中的差异可能是由区域地形以及天气条件引起的。此外,所用数据时空分辨率不同也可能导致分析结果之间的差异。
综合考虑,本文所得结论大体上与前人的研究结果相符,但仍具有一定的差异,研究采用的数据资料类型、时间序列等因素均可能造成这一差异的产生。本文所用数据集的空间分辨率较高,为0.1°,且数据集时间尺度等方面较为有限,虽在一定程度上能够代表深圳市降水演变特征,但为更好地认识该区域的极端降水事件,还需基于更加精细分辨率或更精确的数据进行分析,从而为深圳市的暴雨洪涝灾害预防方案的制定、水资源分配等提供更精确的依据。
近年来,受地理环境以及人文环境的影响,深圳市极端降水的发生具有显著不确定性及突发性。因此,为更加准确掌握深圳市极端降水发生的时段和区域,在下一步研究中,有必要探究各个因素对极端降水的影响机制及多个因素的联合影响机制。
5 结论
基于极端降水指标分析了深圳市极端降水的空间分布特征,同时从降水量以及暴雨日数2方面探究了深圳市极端降水频发地区的极端降水时间变化特征,得到如下结论:
1)深圳市1979—2018年极端降水整体呈从西南向东北递减趋势,极端降水频发地区位置随城市化进程呈从深圳市边缘地区向城市中心迁移的趋势。
2)20世纪90年代,深圳市极端降水频发地区的强降水在1年中的产生时间相较于其他时期发生了滞后,其强度和频率变得更大,可能与这一时期环境污染状况及太平洋10年涛动等因素有关。
3)近40年中,深圳市极端降水频发地区各尺度降水量均无显著变化,除冬季降水量外,其他季节降水量均存在一定的周期性,年暴雨日数均呈小幅下降趋势,年最大日降水量呈小幅上升趋势。

