储能技术在风力发电系统中的应用研究

山西能源学院能源与动力工程系 苏曼婷 刘志刚 王迎春 范敏钧

可持续发展模式在当前社会生产中占据重要位置，其中风能因为具有清洁、可再生等优点成为新能源发展的新方向。但风能受到气象条件、地理环境等因素影响，具有一定的波动性、间接性特征，存在发电量不稳定的特征，而解决上述问题，需要采取一定补偿措施尽可能实现风电输出功率平滑。而储能设备及其相关电力电子技术的出现则充分满足了上述要求，是实现风电并网运行的关键，值得关注。

1 常见储能技术分析

蓄电池储能技术。该技术以电化学形式储能，是较为常见的储能手段，常见技术类型包括镍氢电池技术、铅酸电池技术与锂电池等。根据相关学者对蓄电池技术的调研发现，随着蓄电池技术不断成熟，该技术能量密度大、适应性强等优点而被社会所关注，加之该技术整体成本偏低，也为该技术的发展奠定基础[1]。但该技术存在明显缺陷，如寿命短，加之蓄电池生产制作中使用了有害金属，可能造成环境污染。

超导储能技术。文献[2]对超导储能系统的可行性展开分析，认为该技术的核心思路为：用超导材料制成的线圈把电网供给的电能磁场能量的形式储存，在需要的时再将此电磁能量转换为电能释放出来即可。与常规技术相比，超导储能具有更高的充放电效率，且使用年限长，可在较短时间内提供较大功率，具有技术优势。

超级电容器技术。与传统储能技术方案相比，超级电容器储能技术具有能量存储量大、耐压能力好的技术特点，其技术优势表现为：一是具有更大的功率密度，可满足多次循环充放电的要求，且整个储能系统的运行速度更快。二是该储能技术架构的维护工作量少、系统稳定性高，这也为技术推广奠定了良好基础。

混合储能技术。有学者认为，考虑到单一的储能装置在技术上存在一定的限制，无法同时满足高功率密度、高能量密度、高储能效率等方面的要求，所以应整合不同储能技术的优势实现性能互补，构建的混合储能架构可兼顾技术性能优势与经济性的要求，在兼顾储能系统放电能力的同时，也要尽可能延长使用年限，保证储能技术经济性目标的实现[3]。

2 合储能系统的设计策略

2.1 蓄电池的设计思路

在风力发电中，考虑到风能具有随机性特征，所以为平抑风能输出功率，在储能系统设计中必须考虑两个关键条件，即可以提供长期功率支持，也具有补偿短期高频功率波动的特性。通过对当前常见储能技术的研究可以发现，超级电容技术具有容量小的特征，可满足电力系统频繁充放电的操作要求，并且该技术方案在补偿高频功率波动上具有显著优势。而传统的蓄电池组技术方案虽然无法满足频繁充放电的要求，但作为一种稳定的储能手段，该技术可为风力发电提供长时间稳定的功率支持。基于对上述不同方案的先进性的考虑，在本次混合储能系统设计中，将采用超级电容器+蓄电池组的设计方案。

2.2 蓄电池模型实现

本文所设计的蓄电池模型将电池损耗分为等效内阻损耗与寄生功率损耗两方面，并依靠受控源体现电池性能。与传统蓄电池控制方案相比，本文所设计的电池模型可满足电池荷电状态实时测量的要求，为自动化系统监控蓄电池运行状态奠定良好基础。

本次设计中采用了两个电阻共同实现混合储能系统中的等效内阻，包含了传输电阻、薄膜电阻、反应动力等因素造成的总损耗。在系统结构上采用了多个电池单元串联模式，假设单体电池的电压表示为Ucell，整个混合储能系统中共设有n 个相同的电池，则串联后储能系统的电压计算方式如公式：Ucs=nUcell，式中：Ucs表示储能系统电池堆电压值。同时Ucell与电池荷电状态存在密切关系，则其计算方法如下：

式中：SOC 表示电池的荷电状态；Ueq表示电池正负极标准电势；R 表示气体常数；T 表示温度；F 表示拉法第常数。根据本式所介绍的关系式可以发现，本次设计的混合储能系统中，其性能受到电池电荷状态、单体电池数量等因素影响，此时为确保蓄电池整体性能稳定，则电池组的端电压应满足以下公式的计算要求：Ub=Ues-In（Rreocion+Rresisive），式中：Rreocion与Rresisive分别表示混合储能系统中的两个电阻；Ub表示电池组的端电压。

2.3 电池控制策略

由于本次混合储能系统中采用了超级电容器模型，所以在电池控制策略上应确保电池荷电状态相对稳定，此时SOC 的计算方式如下公式所示：

Soc=U-Umin/Umax-Umin

式中：U 表示超级电容放电时的电压；Umin表示超级电容放电时电压的最小值；Umax表示超级电容放电时电压的最大值。

为更好地满足储能系统控制要求，本次设计中采用超级电容器与双馈风机PWM 变换器，通过直流环节连接的方式，将储能系统连接到风力发电系统中，此时考虑到超级电容器运行期间会导致端电压发生改变，为保证整个系统的稳定性，可考虑引入Buck-Boost 直流斩波电路，该电路的功能是连接电力系统的直流环节与电容器，在整体电路系统结构优化的基础上，利用介入式的拓扑结构可减少风电系统产生的短期功率波动问题，并确保整个电力系统中直流母线强度理想，此时Buck-Boost 直流斩波电路的架构如图1所示。

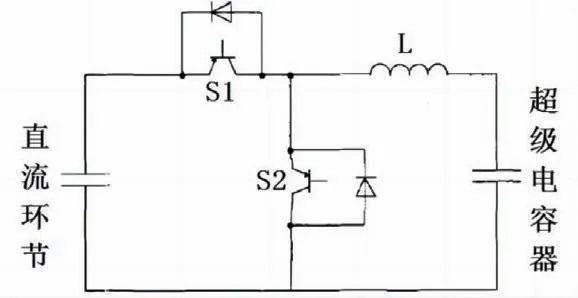
图1 Buck-Boost 直流斩波电路架构图

在图1所介绍的电路架构中，可通过控制两个可控晶闸管调整超级电容器的充放电状态。其中，在混合储能系统的正常工况下，系统通过发送触发信号使S1进入导通状态，确保电能可在直流环节中向超级电容器中释放电能；随着超级电容器中的储能逐渐达到峰值，系统发送闭合系统，在接收触发信号后S1进入闭合状态。但在S1闭合之后风能会持续向系统输送电能，且电感中的电流无法突变，此时电感与S2反并联二极管构成回路，继续执行超级电容充电过程，该过程会支出到开关管S1重新恢复导通，或者能量消失，反之亦然。

由此可见，在图1所介绍的电路架构可控制两个开关管的通断即可控制电路的功率流向，而控制开关管具体的占空比就可控制充放电功率的大小。而为确保图1所介绍的电路架构能稳定持续地运行，应严格控制电路架构的允许最大电流平均值，其计算方法如以下公式所示：

式中：imax表示直流斩波电路的允许最大电流平均值；T 表示超级电容器设定的补偿周期时间；udc风机直流环节的电压值；uess表示超级电容器的电压值；L 表示电路进线的实测电感值。

2.4 储能平抑风电功率波动控制策略

考虑到风能输出的不稳定性，而合理运用储能装置则可平抑风电输出的功率波动，达到提升系统平滑度的效果，这是适应未来大规模风电并网的关键。目前，较为常见的方法包括：在采用单一储能装置平抑功率时，可通过低通滤波器分离补偿功率；在采用混合储能平抑功率时，则可通过高通滤波器与低通滤波器将补偿功率的低频与高频部分分离出来。同时，需要注意的是，在储能平抑风电功率波动控制策略中，可利用低通滤波器获得期望输出功率，但在实际操作中无法完全杜绝延迟效应等因素的影响，这一现象则会导致补偿后的功率值与实际值不相符，导致系统实际需要的储能装置容量更大。

为解决因为上述问题造成的数据差异，本次研究中将引入移动平均值算法，作为一种现代数据分析方法，不同于传统技术对数据的分段，该技术可根据时间轴对数据流程进行推移，在持续获得固定量数据后即可对最终结果进行预测。由此可见，该算法可以提供精准的数据平均值，且数据平滑效果好，可消除因为干扰项等问题对最终结果的精度影响，并综合体现数据变化规律。基于移动平均值算法的要求，在计算风电输出平滑值沟通率中可采用以下公式的计算方法：

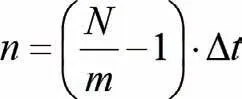
基于上述关系式可以判断，随着n 取值不断增加，m 取值减少，则储能系统对应的期望功率越平滑。同时，m 的取值也是影响期望功率的重要因素，若m 的取值偏低，则会导致曲线出现明显的锯齿状波形。同理为实现混合储能系统稳定运行，则应保证期望功率的平滑度良好，也能与原输出功率曲线保持满意的等值性。

3 系统仿真验证

本次仿真验证中采用MATLAC/Simulink 软件，在该软件中构建风力发电系统仿真模型，在模型运算中设定移动时间尺度n=2s，m=10%。储能装置的仿真设定方案见表1。

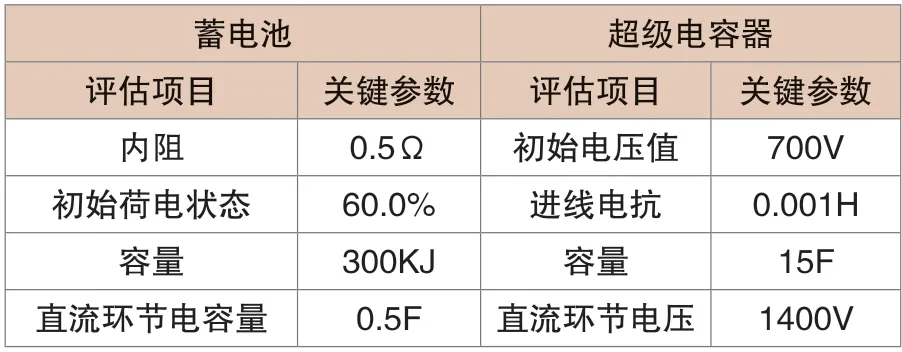
表1 混合储能装置的仿真功能设定方案

同时，为更方便地观察混合储能系统的关键参数，以及电池荷电状态SOC 的变化情况，在本次仿真研究中设定蓄电池容量偏低，确保整个仿真过程可在更短时间达到较大幅度变化的目的。另外，设定该混合储能系统电池荷电状态SOC 的正常值取值范围为15.0%～85.0%，超级电容器的补偿周期为0.004s。

基于上述要求，先对蓄电池系统的SOC 变化情况进行仿真模拟，最终模拟结果显示，蓄电池补偿功率曲线出现了较为明显的数据波动情况，有明显的锯齿状波形，证明在蓄电池补偿功率情况下，SOC的整体情况不稳定。相关数据显示，整个仿真过程以10s 为一个周期，其中当仿真进行至6～8s 时，SOC已经下降至10.4%～12.1%左右，明显偏离正常取值范围。此时，蓄电池处于严重的过充或者过放状态，若不能及时采取有效措施将会导致储能系统使用年限缩短，不利于保证系统的运行稳定性。

之后引入混合储能系统，系统模拟不同时间段的补偿功率变化情况，相关数据对比，在不同仿真时间（s）补偿前/后的风电输出功率情况（单位：×105W）结果如下：0/11.0/11.0、2/9.54 /11.2、4/11.3/10.9、6/8.3/10.4、8/9.4/10.2、10/10.8/10.0。根据以上对混合储能系统应用效果的现场模拟结果可以发现，在通过该储能系统进行补偿后，发现补偿后的输出功率相对平滑，整体波动幅度与补偿前相比整体偏低。

4 创新性评价

本文基于蓄电池组技术、超级电容器技术所构建的混合储能系统在操作上具有可行性，整个数据处理中通过移动平均值算法解决了常规技术存在的数据异常波动情况，并且最终时间结果也显示，该混合储能系统在风力发电系统补偿中具有可行性，经储能装置补偿后，使风电输出功率相对平滑，对于延长蓄电池组使用年限、提升系统稳定性的效果显著。