深度学习背景下小学生提出问题能力现状调查报告

于伟玲 王园

一、调查背景

美国数学家保罗·哈尔莫斯（Paul Halmos）曾说过：“问题是数学的心脏。”《义务教育数学课程标准（2022年版）》提出数学课程要培养学生的核心素养，主要包括“三会”，即会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。其中，“数学眼光”的一个重要含义就是在各种现实和数学的问题情境中，“看”出其中的数学规律，发现和提出有意义的数学问题。然而，一些国际比较研究表明，中国学生善于解决问题，但在发现和提出数学问题方面有所欠缺。要想改变这种现状，那就需要教师把发现和提出数学问题真正作为学生学习数学、理解数学的一种基本方式，进而帮助学生逐步形成和发展“数学眼光”。

为了了解目前新乡市牧野区城区学校小学生提出数学问题能力的现状，课题研究者对该区4所城区学校的小学生进行了问卷抽样调查，以期通过问卷调查结果，分析目前存在问题的根本原因并提出相应的教学建议，从而提升学生提出问题的能力，提高教师课堂教学的质量。

二、调查问卷的设计与实施

（一）问卷内容

学生调查问卷共计15道题目，均为单项选择题。调查问卷的第1—2题是学生的基本信息，第3—15题是学生的主观认知，如表1所示：

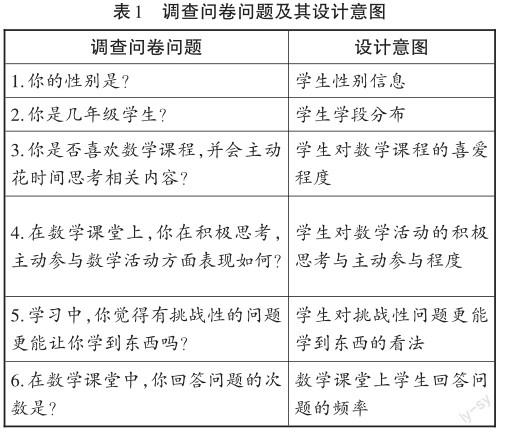
（二）調查对象

本次问卷调查选取的对象为新乡市牧野区4所城区学校的1—6年级部分学生。具体选取要求如下：4所城区学校分别从第一学段、第二学段和第三学段中随机抽取一个常态化教学班级。为了保证调查对象所在年级的均匀分布，本次调查共向随机选取的12个被试班级的全体学生发放纸质问卷630份，回收630份，回收率为100%，其中，有效问卷616份，有效率高达97.78%。

（三）问卷信度与效度

纸质问卷全部回收后，将问卷所有数据录入Excel。由于调查问卷问题分为客观题（1—2题）和主观题（3—15题）两大部分，问卷信度与效度只针对主观题（3—15题）数据进行分析。

1.问卷信度

通过SPSS 27.0对问卷数据的可靠性进行一致性检测，其统计结果如表2所示。由表2可以看到，克隆巴赫Alpha系数为0.704，大于0.7，说明调查问卷具有较高的信度。

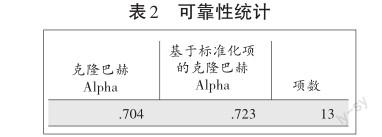
2.问卷效度

通过SPSS 27.0对问卷数据进行KMO和巴特利特检验，其检测结果如表3所示。由表3可以看到，KMO检测系数为0.811，大于0.5。同时，巴特利特球形度检验的显著性概率值小于0.001，说明调查问卷的各个变量之间均具有较强的相关性和较好的结构性。

由以上分析可以知道，本次调查问卷统计的数据信度高、效度好，可以进行具体的研究分析。

三、调查问卷结果与分析

问卷数据进行信度和效度检测后，课题研究者根据部分题目数据统计的特点绘制成统计图，其结果分别如图1至图4所示。

（一）影响学生提出问题的因素

1.数学课堂上学生提出问题的频率

对于问题8：“你在数学课上能提出一些与数学有关的问题吗？”其调查结果如图1所示。

由图1可以看出，选择“偶尔”的人数最多，约占总人数的53.6%。总的来说，学生在数学课堂上提出与数学有关的问题频次较低，并且随着学段的升高，学生从不提问题或偶尔提问题的现象愈发凸显。

2.学生极少或从不提问的原因

对于问题10：“学习中，如果你极少或从不提问，原因是？”其调查结果如图2所示。

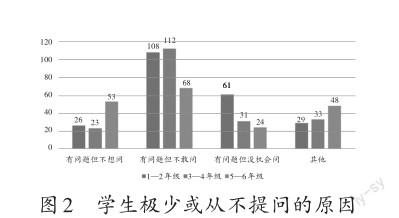
由图2可以看出，选择“有问题但不敢问”的人数最多，约占总人数的46.8%；选择其他三项的，分别约占总人数的16.6%、18.8%和17.8%。各学段的学生极少或从不提问的最大原因均是“有问题但不敢问”，学生为什么有问题却不敢问？他们的内心在担心什么？又在惧怕什么？这是值得教师深思且探寻的地方，也是改变学生极少或从不提问情况的根本原因所在。

3.诱发学生提出问题的学习状态

对于问题12：“你认为在什么情况下最容易提出问题来？”其调查结果如图3所示。