基于多属性效用理论的桥梁可持续性维护策略优化
吴腾
(湖南联智科技股份有限公司, 湖南 长沙 410011)
截至2020年,中国桥梁数量达到90多万座,高居世界首位[1]。在桥梁生命周期内,材料老化、交通负荷及外界环境侵蚀等会影响桥梁的耐久性和安全性,严重时甚至导致结构失效。桥梁失效会带来严重的经济、社会和环境问题[2-3]。为减小桥梁失效带来的不利影响,从经济、社会和环境三方面对桥梁可持续性维护策略进行优化很重要。
桥梁建设和维修阶段都会消耗大量能源和资源,并对周围环境造成影响。近年来,相关学者主要从生命周期环境(LCA)的角度对桥梁维护决策进行优化[4]。Rodrigues J. N. 等从LCA和维护成本等角度研究木材-混凝土复合材料(TCC)替代桥面板的可持续性,结果表明TCC方案对环境的影响较小,且维护成本较小[5]。Xie H. B.等以实质性维护和预防性维护作为基本维护方式,对某混凝土箱梁进行了维护策略优化[6]。目前对考虑桥梁可靠度、维护成本和环境影响的桥梁维护策略优化研究较多,对桥梁可持续性维护策略优化的研究较少。本文基于多属性效用理论,分析桥梁的经济、社会、环境和成本属性,建立基于多属性效用理论的桥梁可持续性维护策略优化模型,并以某桥为例对该优化模型进行验证。
1 桥梁多属性风险评估
1.1 桥梁易损性分析
桥梁服役过程中受到外界氯盐侵蚀、材料退化和交通荷载增加等的影响,桥梁结构性能随时间推移不断退化,进而影响桥梁的正常使用。本文采用桥梁可靠度描述桥梁的性能。桥梁可靠度是指桥梁在使用年限内,考虑环境和结构抗力退化等因素的影响,完成预定功能的能力。在计算桥梁结构可靠度时,先建立极限状态性能函数Z,表达式如下:
Z=R-S=R-MD-ML
(1)
式中:R为桥梁结构的抗弯承载力,按式(2)计算;S为荷载效应;MD为永久荷载作用下产生的力矩,按式(3)计算[7];ML为可变荷载作用下产生的力矩,按式(4)计算[7]。
(2)

(3)
式中:l为梁长;λc为构件静载的相关系数;g1为主梁静载;g2为横隔板静载;λb为路面静载的相关系数;g3为路面静载。
(4)
式中:λd为可变荷载作用下的相关系数;α1为车辆荷载的冲击系数;β1为梁的分布系数;βc为车辆荷载的横向分布系数;qk为车道的均布荷载;pk为车道的集中荷载;βr为人群荷载的横向分布系数;qr为人群荷载。
混凝土碳化及外界氯盐侵入混凝土引起的钢筋锈蚀是导致桥梁结构性能退化的主要原因之一[8-9]。随着锈蚀的发展,锈蚀深度不断增大,钢筋截面面积不断减小,桥梁结构抗力不断退化。锈蚀导致钢筋半径的减少量Δr按式(5)、式(6)计算[10-11]。
Δr(t)=0.116icorr(t-ti)
(5)
(6)
式中:icorr为钢筋锈蚀速率;t为桥梁的服役时间;ti为钢筋开始锈蚀的时间;β为水灰比,β=27/(fc+13.5);fc为混凝土抗压强度;c为混凝土保护层厚度。
1.2 桥梁维护措施的影响
当桥梁的可靠度小于目标可靠度时,应采取相应维护措施对桥梁进行维修加固处理,以保证桥梁的安全运营。本文采用的维护措施主要包括增大截面法、粘贴钢板法、增设体外预应力法及粘贴FRP(纤维增强复合材料)板法。如图1所示,采取维护措施可瞬时提高桥梁可靠度,可按式(1)评估桥梁结构维护效果。

图1 维护措施对桥梁可靠度影响示意图
1.3 与桥梁相关的风险属性评估
风险属性Q由特定事件发生的概率与该事件发生的结果组成,是综合评估桥梁维护策略的重要指标,表达式如下:
Q=pγ
(7)
式中:p为特定事件发生的概率;γ为该事件发生的结果。
本文研究的风险属性主要包括经济属性、环境属性和社会属性。
1.3.1 桥梁的经济属性
经济属性QEC主要指桥梁的维护成本,可表示为[12]:
(8)
式中:Pf(t)为服役时间t时桥梁结构的失效概率;Ca为桥梁失效时重建或维护的成本;r为贴现率,根据文献[13],r=0.03。
1.3.2 桥梁的社会属性
社会属性主要指由于桥梁故障导致的绕行距离和绕行时间及由桥梁结构失效导致的伤亡事故。与绕行时间相关的风险属性QTT可表示为[12]:
(9)
式中:α为非卡车车辆的占用率;PTR为卡车占平均日交通量的百分比;QADT(t)为第t年的平均日交通量;Ls为绕行距离;Td为绕行持续天数;v为平均绕行速度。
与绕行距离相关的风险属性QTD可表示为[13]:
QTD(t)=Pf(t)LsQADT(t)Td
(10)
伤亡事故的风险属性QTF可表示为[14]:
(11)
式中:L为桥梁全长;la为汽车安全跟随距离。
1.3.3 桥梁的环境属性
环境属性主要指由于绕行和桥梁维护活动产生的能源消耗及二氧化碳排放。由于绕行而产生的二氧化碳排放量的风险属性QENV,CO2,1可表示为:
QENV,CO2,1(t)=Pf(t)QADT(t)Ls×
(12)
式中:Qcpdc、Qcpdt分别为小汽车和卡车行驶单位距离的二氧化碳排放量。
由于绕行而导致的能源消耗的风险属性QENV,E,1可表示为:
QENV,E,1(t)=Pf(t)QADT(t)LsTdQepd
(13)
式中:Qepd为汽车或卡车行驶单位距离的能源消耗。
除考虑由于绕行造成的环境影响外,还要考虑桥梁长期服役过程中钢筋锈蚀和交通荷载等因素作用对桥梁结构损坏造成的环境影响。桥梁维护活动产生的二氧化碳排放量的风险属性QENV,CO2,2和能源消耗的风险属性QENV,E,2分别表示为[15]:
QENV,CO2,2(t)=Pf(t)QCD,CO2
QENV,E,2(t)=Pf(t)QEC,E
(14)
式中:QCD,CO2、QEC,E分别为桥梁维护活动产生的二氧化碳排放量和能源消耗,可根据文献[13]计算得到。
综上,桥梁在第t年的二氧化碳排放量和能源消耗对应的风险属性QCO2(t)、QE(t)可表示为:
QCO2(t)=QENV,CO2,1(t)+QENV,CO2,2(t)
(15)
QE(t)=QENV,E,1(t)+QENV,E,2(t)
(16)
2 桥梁可持续性的多属性效用理论评估
效用理论是决策者对方案进行对比选择时采用的一种方法。方案选择通常受决策者主观意志的影响,决策者对事物进行决策时须考虑目前所处环境及未来发展,对可能存在的利益和损失作出取舍,通常把决策者对于利益和损失的特有兴趣、反应或取舍称为效用[16-17]。效用可以体现决策者对于风险的态度,风险态度的表现形式主要包括风险追求、风险中立和风险规避(见图2),高风险通常会带来高回报。不同的决策者对待不同方案采取的态度和选择不同。

图2 效用函数示意图
鉴于各属性(经济属性、环境属性和社会属性)的单位不同,根据效用理论对各属性进行无量纲化处理。对于效益型属性,按式(17)进行无量纲化处理;对于成本型属性,按式(18)进行无量纲化处理。
(17)
(18)
式中:max(xi)和min(xi)分别为所有属性值中的最大值和最小值;xi为属性值。
根据式(17)、式(18),考虑决策者对待风险的态度,建立桥梁可持续评估中与各风险属性相关的效用函数Uf如下:
(19)
式中:γ为风险态度,通常取-1≤γ≤1,γ=1表示风险规避,γ=-1表示风险追求;f1(x)为属性无量纲化函数,表达式见式(20)。
(20)
式中:Qmax、Qmin分别为所有属性值中的最大值和最小值;Qf为属性值。
在得到与各风险属性相关效用函数后,可对其进行加权计算,得到具有代表性的桥梁可持续性效用值Us如下:
Us=α1Uec+α2Uso+α3Uen
(21)
式中:Uec、Uso、Uen分别为经济属性、社会属性和环境属性对应的效用函数;α1、α2、α3分别为上述属性对应的权重因子,α1+α2+α3=1,本文取α1=α2=α3=1/3。
成本效用函数Qc如下:
(22)
(23)
式中:Cmax为最大维护成本;Cc为所选维护策略的成本。
多属性效用理论的分析流程见图3。

图3 桥梁可持续性的多属性效用分析流程
3 基于改进粒子群算法的桥梁维护策略优化
桥梁维护策略优化的目标是在维护年限内,桥梁的可持续性效用Us最大、成本效用Uc最小,是一个多目标优化问题,采用改进粒子群算法对该多目标优化问题进行分析。
3.1 传统粒子群算法
粒子群算法(PSO)是一种基于群体的随机优化算法,源于对鸟群寻找栖息地和群体觅食的模拟。PSO使用随机生成的粒子群(初始群)进行初始化,并为每个粒子分配随机速度,这些粒子在搜索空间中通过多次迭代逐渐向最优解靠拢,直至找到最优解。每个粒子都有记忆性,可以记住它过去所达到的最佳位置即粒子最佳位置(Pbest)。每个粒子都有其Pbest,具有最佳适应度值的粒子称为全局最佳粒子(Gbest)。每次迭代时,根据式(23)、式(24)分别改变粒子的速度和位置:
(24)
(25)
式中:k为迭代次数;d=1,2,3…,D;D为搜索空间维度;i=1,2,3…,N;N为种群大小;w为惯性权重因子;c1、c2为学习因子;r1、r2为均匀分布在[0,1]之间的随机数。
3.2 算法改进
传统粒子群算法存在易陷入局部最优、早熟收敛、搜索精度较低等不足,须对其进行改进。研究表明,惯性权重因子w越大,粒子的飞行速度越快,全局寻优能力越强;w越小,算法易陷入局部最优。因此,通过改变w的取值方式可以有效提高算法的性能。本文将动态非线性递减惯性权重的思想引入粒子群算法中,表达式如下:
(26)
式中:wmax、wmin分别表示惯性权重因子的最大值、最小值;kmax为最大选代次数。
4 算例分析
4.1 工程概况
以某预应力混凝土空心板梁桥为例对上述优化方法进行验证。该桥全长120.0 m,桥面宽15.5 m,桥面铺设10 cm厚C50混凝土和10 cm厚沥青混凝土,设计使用年限为100年。桥梁横截面见图4。

图4 桥梁横截面示意图(单位:mm)
4.2 桥梁风险属性和效用分析
用于计算该桥风险属性的相关参数[18-21]见表1。根据式(19)~(21),计算得到无维护活动下时变多属性效用值及年度各风险属性效用值(见图5),风险态度γ取1,即图5所示为风险规避下时变效用曲线。
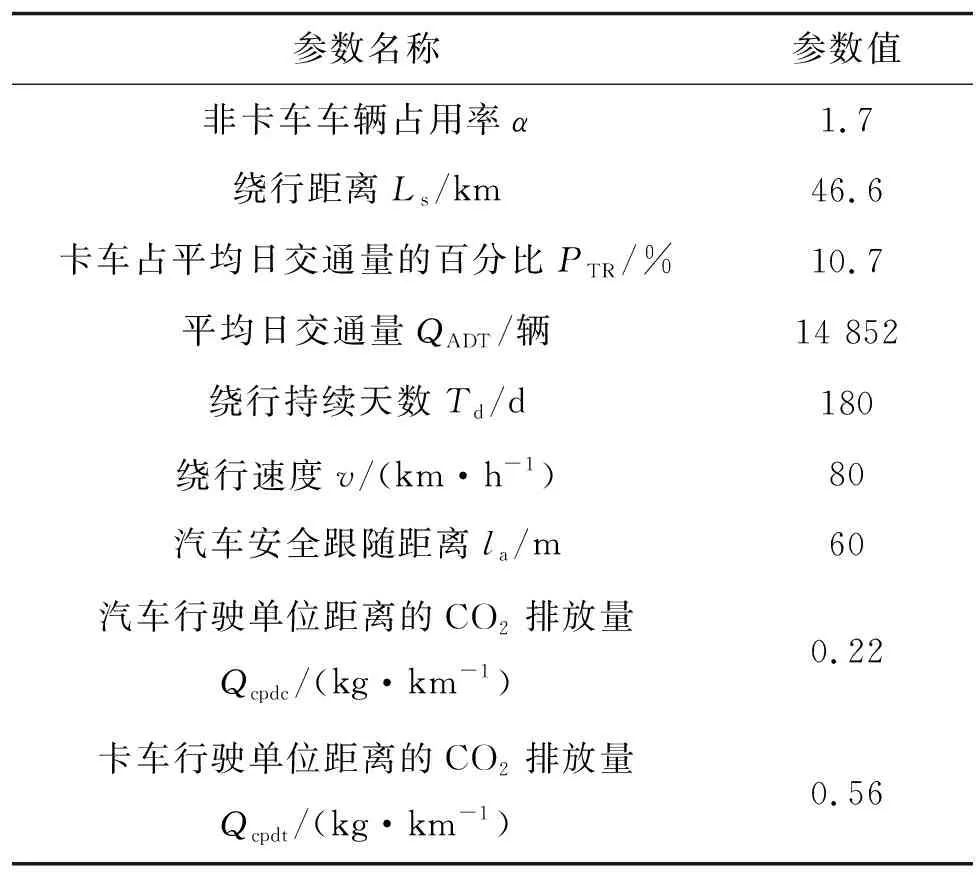
表1 用于计算桥梁风险属性的相关参数

图5 桥梁无维护措施下的效用值
从图5可以看出:在无维护措施的情况下,该桥的经济、社会和环境效用及可持续性的多属性效用在其生命周期内均由1下降至零,其中经济效用值的下降趋势最明显,表明桥梁失效概率的增加对经济效用的影响最大。
4.3 基于粒子群算法的桥梁最优维护策略
采用改进粒子群算法对该桥进行多目标优化,运用MATLAB计算风险追求和风险规避下帕累托最优解集,从中分别选择3种维护策略(见图6)。从图6可以看出:风险规避下可持续性效用和维护成本比风险追求下可持续性效用和维护成本大;M1和N1为不同风险态度下可持续性效用较优的维护策略,M2和N2为综合考虑可持续性效用和成本效用的维护策略,M3和N3为成本效用较优的维护策略。

M1、M2、M3和N1、N2、N3分别表示风险追求和风险规避下最优维护策略
表2为代表性最优维护策略及其效用,包括维护措施、维护时间及维护成本效用和可持续性效用。图7、图8分别为在风险追求和风险规避下各代表性最优维护策略的可持续性效用变化曲线。

表2 代表性最优维护策略及其效用
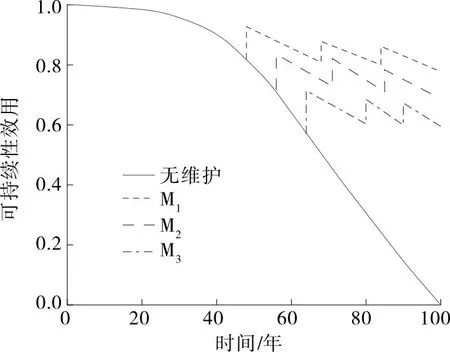
图7 风险追求下可持续性效用变化曲线

图8 风险规避下可持续性效用变化曲线
从图7、图8可以看出:在桥梁生命周期内,采取维护加固措施可以有效提高桥梁可持续性效用值,使桥梁整体处于效用较高的状态,有效保证桥梁的安全运营;风险追求下可持续性效用值整体比风险规避下可持续性效用值小;分析相同风险态度下各代表性最优维护策略,维护成本效用较优的维护策略M3、N3的可持续性效用较低,而可持续性效用较优的维护策略M1、N1的维护成本较高,在选择桥梁维护加固策略时,只考虑成本属性或可持续性效用较片面,对环境、经济及社会属性进行综合分析是得到较优维护成本和可持续性维护策略的有效方法。
5 结论
本文考虑钢筋锈蚀和结构退化等因素建立桥梁时变可靠度计算方法,基于多属性效用理论研究桥梁的经济属性、社会属性和环境属性,建立基于多属性效用理论的桥梁可持续性维护策略优化模型。以某桥为例,基于改进粒子群算法,以可持续性效用最大和成本效用最小为优化目标,利用该优化模型进行多目标优化,得到该桥的最优维护策略。主要结论如下:
(1) 在桥梁生命周期内,采取维护加固措施可以有效提高桥梁可持续性效用值,使桥梁整体处于效用较高的状态。
(2) 在选择桥梁维护加固策略时,只考虑成本属性或可持续性效用较片面,对环境、经济及社会属性进行综合分析是得到较优维护成本和可持续性维护策略的有效方法。
(3) 不同的风险态度得到的最优维护策略不同,风险追求下可持续性效用值整体比风险规避下可持续效用值小。
(4) 利用该优化模型,采用改进粒子群算法可得到一组最优维护策略,决策者可根据维护成本、可持续性效用及风险属性选择满足自身需求的最优维护策略。

