基于CRITIC和AHP组合赋权的TOPSIS法蜂群威胁评估研究

和烨龙，张鹏飞，赵永娟，王智伟，冀云彪

(1.中北大学 机电工程学院，山西 太原 030051；2.中北大学 智能武器研究院，山西 太原 030051)

随着空天武器装备的迅速发展,空中目标的威胁已经不仅仅来源于各型战机和各类导弹,从近年来纳卡冲突、俄乌冲突等局部战争中敌对双方不断使用无人机蜂群对某些重要目标进行侦察打击[1],可以看出无人机蜂群在现代战场中有着非常重要的战术地位,对于来袭无人机蜂群的威胁评估是实现有效拦截不可或缺的一环。无人机蜂群威胁评估是根据来袭目标对我方产生威胁的各种因素建立威胁评估指标体系和使用科学合理的数学方法对威胁程度进行评估。根据评估流程不同,无人机蜂群威胁评估方法可以分为直接对威胁指标进行评估和通过机器学习训练再进行评估两类。第一类评估方法包括不赋权直接评估法[2]、单一主观或客观赋权评估法[3-8]和组合赋权评估法[9-16],不赋权直接评估法存在没有考虑评估指标间更重要程度的问题,单一主观或客观赋权评估法存在只从主观或客观考虑确定指标间更重要程度的问题,组合赋权评估法存在不考虑主、客观权重之间的更重要程度,仅将主客权重各取一半线性组合的问题。第二类评估方法利用神经网络对目标威胁进行评估[17],但是现有研究中存在机器训练数据库过小的问题,虽能证明预测方法的可行性但不能验证其准确性。

针对以上问题,笔者提出了以静态指标和动态指标建立威胁评估指标体系,运用博弈思想对层次分析法(Analytic Hierarchy Process,AHP)得出的指挥员决策主观权重和CRITIC法(Criteria Importance Though Intercrieria Correlation,CRITIC)得出的数据客观权重进行组合优化,使用优劣解距离法(Technique for Order Preference by Similarity to an Ideal Solution,TOPSIS)对无人机蜂群目标进行威胁评估排序,充分考虑静、动两类评估指标和主、客观两种评估角度,使评估结果具有合理性和可行性。

1 威胁度评估指标体系建立

笔者采用的威胁评估指标体系分为静态指标组成的无人机战术参数指标、动态指标组成的蜂群战场战术动态指标和蜂群战场环境条件指标3个一级指标,如图1所示。无人机战术参数指标由有效载荷、续航能力、最大飞行速度、作战半径4个定量二级指标组成;蜂群战场战术动态指标由蜂群组合威胁数、飞行速度、飞行高度、航路捷径、来袭斜距离、来袭方向角6个定量二级指标组成;蜂群战场环境条件指标由气象条件、地形优劣条件、电磁干扰条件3个定性二级指标组成,综上指标构建出无人机蜂群威胁评估体系。

除了常规评估指标,由于作战任务不同会产生不同的无人机蜂群组合,提出了蜂群组合威胁数这一评估指标,该指标是通过静态指标的评估结果根据蜂群中无人机目标的数量和种类建模：

Fk=∑(VlGl),

(1)

式中：k为蜂群的编号;l为蜂群中的第几种无人机目标;Fk为编号k的蜂群中无人机目标威胁评估结果线性叠加后形成的蜂群组合威胁数;Vl为静态指标威胁评估后第l种无人机目标对应的评估结果;Gl为编号k的蜂群中第l种无人机目标的数量。

2 评估指标权重确定

2.1 指挥员评估决策权重确定

战争中指挥员是军队的大脑,其战术谋略和军事能力是一场战争能否取胜的重要原因,直接体现了军队建设水平的高低,因此根据指挥员作战经验等实际情况进行威胁评估产生主观决策权重作为主观权重。通过层次分析法确定主观决策权重包括判断矩阵生成、判断矩阵一致性检验和决策权重计算三部分。

2.1.1 判断矩阵生成

以动态指标为例,权重判断矩阵的生成由指挥员结合各种战场因素和自身经验,给每一个动态指标在层次分析强度表中取值,并对每个评估指标的取值两两取比值,生成动态指标权重判断矩阵T：

(2)

式中：m=1,2,…,t;n=1,2,…,t;t为评估指标个数;znm为第n个指标在层次分析表中的取值与第m个指标在层次分析强度表中的取值之比,能够体现两种评估指标之间的更重要程度,具体强度等级划分如表1所示。其中：2、4、6、8表示介于相邻两个强度之间。

表1 层次分析强度表

2.1.2 判断矩阵一致性检验

为了防止评估指标之间出现诸如飞行速度比飞行高度重要、飞行高度比航路捷径重要且航路捷径比飞行速度重要的矛盾情况,所以要进行一致性检验,检验过程如下：

1)对动态指标权重判断矩阵进行归一化处理,并且求出归一化矩阵的最大特征值λmax。

2)计算一致性比例RC：

RC=IC/IR,

(3)

式中：IC=(λmax-t)/(t-1),λmax为归一化矩阵的最大特征值;IR通过查随机一致性表[18]得出,随机一致性值如表2所示。

表2 随机一致性表

若0≤RC<0.1,则认为一致性检验通过,否则需要对判断矩阵中的指标重要程度之比进行调整,直至一致性检验通过。

2.1.3 决策权重计算

一致性检验通过后,将归一化动态指标权重判断矩阵进行权重计算,形成动态指标主观决策权重向量ω1,其中各指标的主观权重为

(4)

同理,可得出静态指标主观决策权重向量。

2.2 CRITIC法的客观权重确定

CRITIC法是一种客观权重赋权法,此方法相比于信息熵和变异系数法完全利用数据自身的客观属性,综合考虑指标的对比强度和冲突性,对于多指标多对象的综合评估问题,消除了一些相关性较强指标之间的影响,减少了指标之间的信息叠加,得出的结果更加客观可信,因此,选用CRITIC法权重赋权作为客观权重。使用CRITIC法确定客观权重包括构造参数判断矩阵和计算CRITIC客观权重。

2.2.1 构造参数判断矩阵

以动态指标为例,假设对p个来袭目标的q个指标进行威胁评估,根据己方雷达探测侦察的战场实况信息构造参数判断矩阵A：

(5)

式中,apq为第p个来袭威胁目标的第q个评估指标。

对参数判断矩阵中的每个元素进行正向化和归一化处理,得到归一化矩阵B：

(6)

式中,正向化的方法不固定,由于本文数据都为正,所以采用取倒数的方法进行正向化和归一化过程：

(7)

式中：i=1,2,…,p;j=1,2,…,q。

2.2.2 计算CRITIC权重

归一化矩阵B计算指标变异性Sj：

(8)

计算指标冲突性Rj：

(9)

式中,rij为评估指标i和j之间的相关系数。

计算信息量Cj：

(10)

CRITIC客观权重向量ω2,其中各指标的客观权重为

(11)

2.3 基于博弈思想的权重优化

博弈思想是研究多人谋略和决策问题的思想,博弈思想的决策至少有两个存在竞争关系的博弈者,且他们之间相互依存、相互较量,都会为了实现自身利益最大化采取行动,最终这场博弈会处于有限条件下双方利益最大化的均衡状态。

根据博弈思想进行权重优化,其过程是将主观权重向量ω1和客观权重向量ω2作为博弈局中的双方,当博弈双方到达纳什均衡状态,即采用最小离差找到纳什均衡解时,指标权重最合理。权重优化过程包括以下四步：

步骤1将博弈双方进行线性组合：

ωy=ε1ω1+ε2ω2,

(12)

式中,ε1和ε2是主观权重向量的权重因子和客观权重向量的权重因子。

步骤2构建最小离差函数[10]：

min(‖ωy-ω1‖2+‖ωy-ω2‖2).

(13)

步骤3根据微分原理将上述最小离差函数转换为最优化一阶导数方程组：

(14)

(15)

(16)

3 威胁评估方法

TOPSIS法是解决多属性决策问题的有效方法。此方法是通过计算评估对象与最优解、最劣解的距离来进行排序,若评估对象最靠近最优解同时又最远离最劣解,则为最优;否则不为最优。其中最优解的各指标值都达到各评价指标的最优值,最劣解的各指标值都达到各评价指标的最劣值。TOPSIS法计算评估过程包括以下三步：

步骤1从归一化矩阵B中取出定义的最优值集合B+和最劣值集合B-：

(17)

(18)

步骤3计算i个目标与最优的贴合程度：

(19)

式中：i=1,2,…,p;j=1,2,…,q;Ei越大越接近最优值。

4 仿真分析

在俄乌冲突中,双方使用大量无人机蜂群侦察打击,以俄对乌的6种无人机型号构建无人机战术参数表,如表3所示。

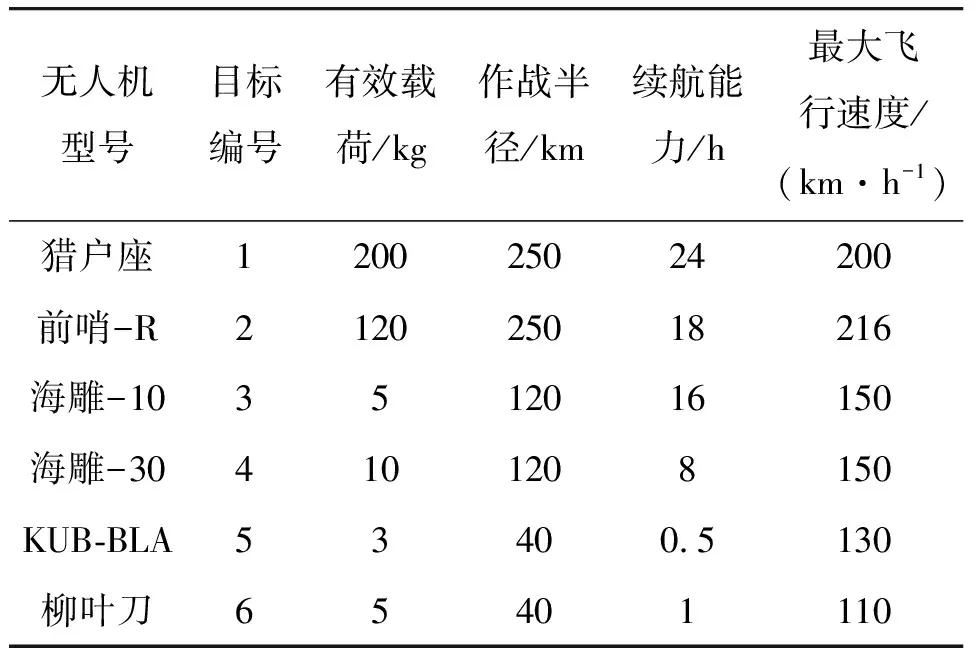
表3 俄对乌无人机战术参数

依据环境条件对蜂群的影响程度,在层次分析强度表中,对蜂群战场环境条件指标取值,构建蜂群战场环境条件表,如表4所示。

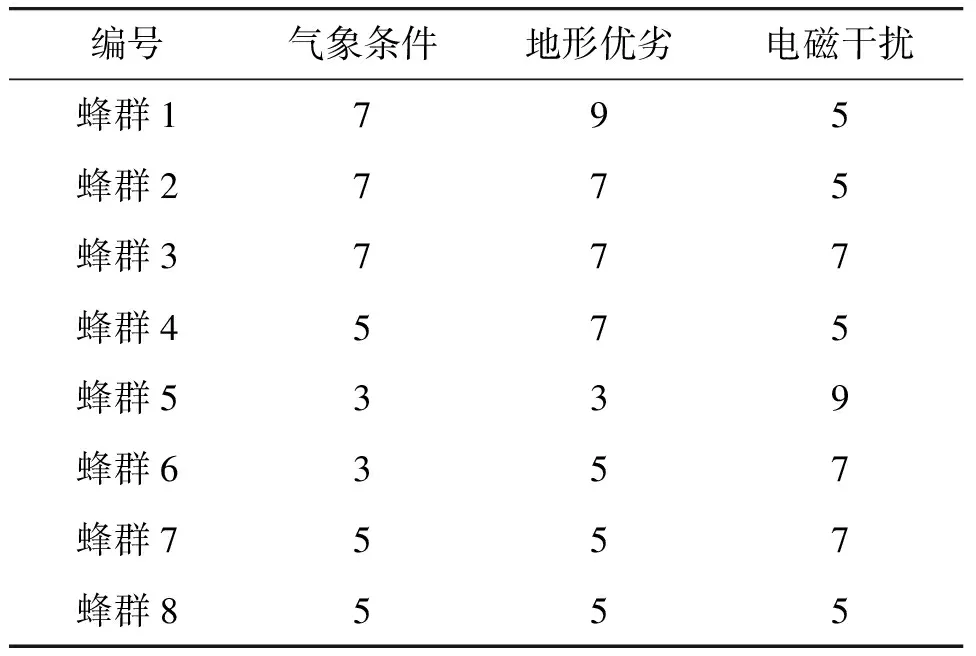
表4 蜂群战场环境条件

通过对俄乌冲突的资料进行搜集分析并假设俄方雷达等探测设备侦察到的来袭蜂群战场战术动态数据,构建3个来袭蜂群的战场战术动态表,如表5～7所示。由式(2)和表(1)构建静态指标权重决策表和动态指标权重决策表,如表8～9所示。

表5 第1个来袭蜂群战场战术动态

表6 第2个来袭蜂群战场战术动态

表7 第3个来袭蜂群战场战术动态

表8 静态指标权重决策表

提取表8和表9中的评估指标数据,由式(2)分别形成权重决策矩阵并求可得静态指标权重决策矩阵特征值λmax=4,动态指标权重决策矩阵特征值λmax=9.027 0。

表9 动态指标权重决策表

由式(3) 可得,静态指标一致性检验RC=0,动态指标一致性检验RC=0.002 3。一致性检验结果<0.1,全部通过一致性检验。

通过式(4)计算指挥员主观决策权重向量可得

ω1=[0.058 3,0.174 8,0.087 7,0.136 0,0.136 0,
0.083 3,0.100 6,0.060 4,0.162 9]。

由式(5)～(11)计算动态指标参数判断矩阵中各指标的CRITIC客观权重,可得：

(ω2)1=[0.142 9,0.082 3,0.123 9,0.065 6,0.063 4,0.051 5,0.170 0,0.150 2,0.150 2],
(ω2)2=[0.138 8,0.084 7,0.130 3,0.069 1,0.066 7,0.053 9,0.175 6,0.141 0,0.139 8],
(ω2)3=[0.163 4,0.083 9,0.148 7,0.069 1,0.065 6,0.053 2,0.170 1,0.123 0,0.123 1].

静态指标可以由指挥员直接判断出来影响程度,故不需进行权重优化,由式(12)～(14)对动态指标权重进行组合优化,可得ε1=0.526 5、ε2=0.561 9。

由式(16)计算优化权重,可得：

由式(17)～(18)计算最优距离和最劣距离可得：

由式(19)计算威胁系数可得：

V=[0.979 4,0.685 0,0.295 7,0.210 0,0.025 7,0.012 4],
(Ei)1=[0.596 6,0.532 6,0.500 5,0.400 0,0.211 0,0.238 8,0.510 1,0.578 3],
(Ei)2=[0.614 3,0.547 6,0.496 1,0.402 1,0.220 6,0.253 1,0.577 5,0.577 1],
(Ei)3=[0.595 8,0.562 6,0.473 7,0.404 9,0.185 3,0.241 0,0.430 5,0.444 7].

除了计算优化权重的贴合度外,数值仿真过程中还计算了单一层次分析法权重和单一CRITIC法权重这两种情况的贴合度,如图2～4所示。

无权重评估时可以看作每个评估指标所占权重都相等,即每个指标的权重平均值为1/指标个数,仿真分析中这个权重平均值为1/9,大于该平均值可以看作权重赋予偏向。3个来袭蜂群的仿真分析结果表明,在无权重TOPSIS威胁评估这一基础评估方法上,使用单一层次分析法赋权,由ω1可以看出评估指标权重会偏向飞行速度、航路捷径、斜距离和电磁干扰这4个指标,使TOPSIS评估结果排序按照这5个指标进行偏向排序;使用单一CRITIC法赋权,由案例仿真中全部的ω2可以看出评估指标权重会偏向方向角、飞行高度、气象条件、地形优劣和电磁干扰这5个指标,使TOPSIS评估结果排序按照这5个指标进行偏向排序。以上两种赋权方法都是威胁评估中指标赋权的常用方法,都具有一定的可信度,但是它们对本文仿真案例给出相反的威胁评估排序,说明单一主客观角度对指标权重赋予偏向不同,会使蜂群威胁评估结果按照权重赋予偏向进行偏移,导致威胁评估结果产生片面的排序变化,此时威胁评估结果排序考虑角度不够全面,不具有足够的说服力。

优化权重TOPSIS威胁评估充分结合层次分析法主观权重和CRITIC法客观权重的赋予偏向,运用博弈思想给出考虑角度全面的优化权重,加强两种单一赋权共同偏向的影响,同时弱化单一赋权偏向分歧指标的权重影响,使TOPSIS对两种单一赋权法歧化排序的部分进行穿插排序,这种融合主客角度的威胁评估结果排序更加合理,更有参考价值。

综上所述可以总结得出本文方法相比于其他两种方法考虑的因素更加全面,给出的威胁评估排序更加符合后续火力分配工作的开展要求。

5 结束语

笔者从静态指标无人机战术参数指标、动态指标无人机蜂群战场战术动态指标和无人机蜂群战场环境条件指标进行考虑,提出了结合动态指标和静态指标的蜂群组合威胁数这一评估指标,构建出更加合理的威胁评估体系。然后从主观因素和客观因素两个角度分别计算了指挥员主观决策的层次分析法权重和客观上完全由指标数据决定的CRITIC法权重,结合博弈思想对主观权重和客观权重进行了组合优化,最后结合TOPSIS方法进行蜂群威胁评估排序,威胁评估结果排序的对比证明了论文研究思路方法的可信可行。

在实际的战场情况下,基于本文所建立的威胁评估体系和评估方法,只需针对性的依据战场态势变化,及时更新威胁评估数据和调整相对应指标的权重,就能计算出符合实时战场需求的威胁评估结果排序,提高作战效能。