基于实测数据的高海拔大日温差地区拱上组合梁桥-无砟轨道体系温度场研究
勾红叶,陈子豪,刘 畅,肖 畅,袁 蔚,苏延文
(1.西南交通大学 土木工程学院,四川 成都 610031;2.中铁第四勘察设计院集团有限公司,湖北 武汉 430061;3.中铁二院工程集团有限责任公司,四川 成都 610031;4.中国铁道学会 标准与认证部,北京 100844;5.兰州交通大学 土木工程学院,甘肃 兰州 730070)
钢-混凝土组合结构桥梁因其优异的力学性能和施工优势,已在我国的不同地区得到了推广应用。一方面,由于钢梁与混凝土桥面板的传热性能差异,在日照升温过程和夜间降温过程中,桥梁结构会产生较大的竖向温度梯度[1-2]。尤其是在高海拔大日温差地区,受复杂环境因素影响,周期性正负温度梯度作用更加显著[3]。另一方面,在铁路组合梁桥铺设无砟轨道时,还需要考虑无砟轨道对于桥面板的遮蔽作用。因此,亟需准确描述高海拔大日温差地区桥梁-轨道结构体系的整体温度分布特征,提出适用于该地区的温度梯度荷载。
为探寻组合梁桥温度场的分布规律,需要准确描述结构的热边界条件。文献[3-9]采用模型试验、数值模拟等方法,分析了结构形状、方位、环境温度、对流换热系数和太阳辐射参数等热边界条件影响因素对组合梁温度分布的影响。针对我国高海拔地区,文献[10-11]结合当地历史气象数据和气候特点,对仿真的热边界条件进行了优化,归纳了组合梁结构竖向温差分布特点。
针对热边界条件中的太阳辐射模型方面,现有的直散分离模型可以分为经验模型、机器学习模型及卫星数据反演模型等[12]。翁笃鸣等[13-14]根据青藏高原夏季的散射辐射状况,研究了大气透明度、海拔和云量等环境参数对散射辐射的影响,提出适用于青藏高原地区的直散分离模型。薛俊青等[15]在融合Hottel模型与ASHRAE模型的基础上,分别计算了太阳直射辐射和散射辐射,并基于气象站逐时太阳辐射等气象参数验证了模型对混凝土箱梁的适用性。
针对桥梁竖向温度梯度荷载的代表值问题,学者们大多倾向于采用概率统计或极值估计方法进行计算,统计数据来源于长期结构监测数据或基于气象数据的有限元数值模拟结果[2]。戴公连等[16]基于长期结构温度监测数据,采用高阶矩法得到了高速铁路混凝土梁-轨道体系竖向温度梯度在不同超越概率下的阈值。Tong等[17]和Ding等[18]采用Gumbel分布、Weibull分布等极值分布模型描述了桥梁的竖向梯度极值分布。张欢等[19]提出考虑参数更新的广义帕累托分布(generalized Pareto distribution,GPD)模型,描述组合梁竖向温差极值分布,并依据不断更新的温度监测数据对模型进行修正。
综合来看,在待建桥梁地区地形气候复杂时,很难通过结构的长期结构温度监测数据直接获得其温度场分布特征;现有的数值模拟研究对于结构温度场的模拟方法和关键参数选取也存在差异[6]。当太阳辐射模型应用于不同地区时,仍然需要重新计算与环境相关的各类参数[2],且大多数研究仅选取晴朗天气下的直散分布理想状态作为依据,结果难以体现桥梁结构的温差极值分布规律。此外,目前鲜有针对高海拔大日温差地区与铁路拱上组合梁桥-无砟轨道体系温度场的研究。
有鉴于此,针对我国高海拔大日温差地区拟建铁路桥梁温度场分布难以精准描述的问题,本文基于桥址地区环境温度监测数据和卫星反演得到的太阳辐射数据,建立拱上钢-混凝土组合梁桥与双块式无砟轨道体系温度场模型,重点分析结构温度场的变化规律,获得了竖向温差分布特征和考虑环境因素随机作用的全年竖向温差样本。在此基础上,利用极值分布估计理论估算该地区拱上组合梁桥-无砟轨道体系的竖向温度梯度设计推荐值,可为特殊地区桥梁温度作用的确定提供参考。
1 温度场与温差极值计算方法
1.1 结构温度场热边界条件
在太阳辐射、环境温度和风速等气象因素的作用下,桥梁-轨道体系在服役过程中会产生复杂的三维非线性瞬态温度场,准确模拟热边界条件是保证数值模型准确性的关键。结构温度场边界条件示意见图1。
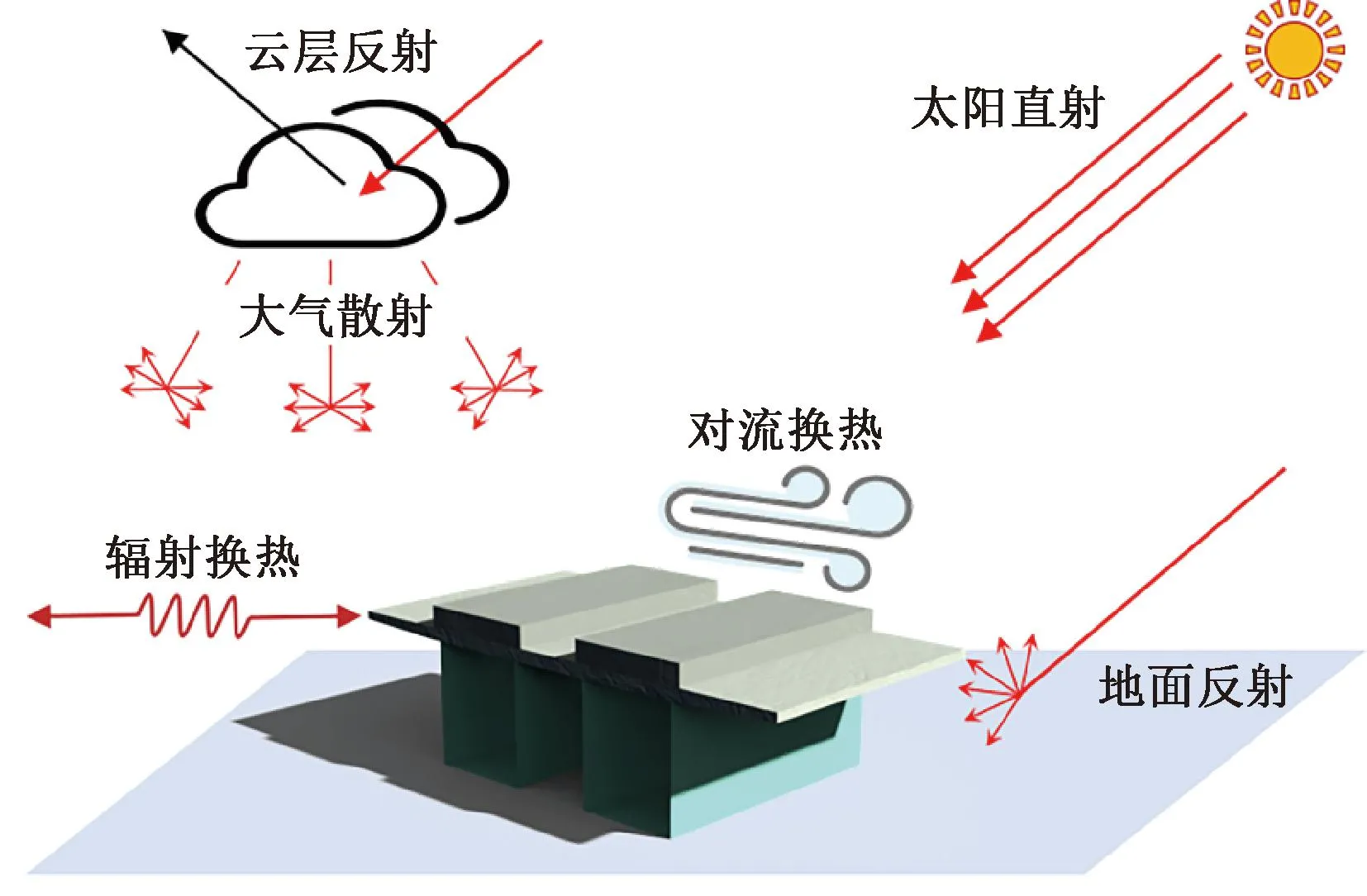
图1 结构温度场边界条件示意
模型的热边界条件主要包括太阳辐射、对流换热和辐射换热三种。太阳辐射又可分解为太阳直接辐射、大气散射辐射和地面反射辐射[6]。
1.1.1 太阳辐射
太阳辐射不同分量对结构的作用方式是影响模拟精细程度的关键要素。结构在日照条件下接受到的太阳辐射热流密度qs可表示为[20]
qs=αI=α(Idh+Ish+Igr)
(1)
式中:α为结构表面对太阳辐射的短波吸收率;I为结构表面的总太阳辐射强度;Idh为结构表面直射辐射强度;Ish为结构表面散射辐射强度;Igr为结构表面反射辐射强度。
1)太阳辐射强度计算
基于卫星数据反演的散射比模型,通过得到的桥址地区实时散射率(diffusecoefficient)和晴空指数(clearnessindex)对大气层的散射效应进行量化。其中,直散分离模型采用基于晴空指数与散射率的多参数直散分离模型[12],模型输入参数均采用卫星反演数据。地表水平面的太阳直接辐射Idh0和大气散射辐射Ish0在一天中不同时刻的大小分别为
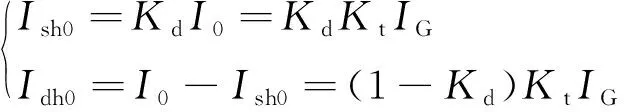
(2)
式中:Kt、Kd分别为在一天中某一时刻的晴空指数、散射率,基于卫星反演结果得到;IG为卫星测量的大气上界太阳辐射平均值;I0为地表水平面的所有天空日照辐射之和。
2)太阳辐射角度计算
为确定任意时刻下太阳相对结构表面的直射方向,需要获取结构地理参数和表面方向参数。地理参数方面,采用文献[21]中的方法得到太阳赤纬角δ、太阳高度角β和太阳方位角φ。表面方向参数方面,结合太阳入射方向、结构外表面位置及其外法线方向信息,可以计算得到任意倾斜面的太阳直接辐射入射角和散射辐射角度,即
(dx,dy,dz)=(cosβcosφ,sinβ,cosβsinφ)
(3)
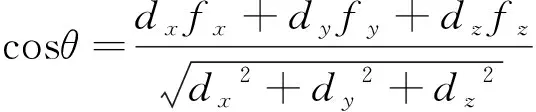
(4)
cosγ=fy
(5)
式中:θ为阳光直射逆向方向与结构面外法线的夹角;γ为结构面切向与水平面的夹角;(fx,fy,fz)为结构外表面法线单位向量(y向为垂直水平面方向);(dx,dy,dz)为阳光直射逆向向量。
依据角度信息得到结构表面的直射、散射和反射辐射强度[22]分别为
Idh=Idh0cosθ
(6)
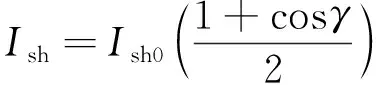
(7)
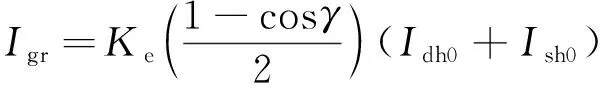
(8)
式中:Ke为地表辐射反射率。
1.1.2 对流换热与辐射换热
当结构表面与外界自然环境存在温度差时,会产生相应的热量交换,即对流换热。对流换热边界条件采用牛顿冷却方程表示为[23]
qc=hc(Ts-Ta)
(9)
式中:qc为对流换热的热流密度;hc为对流换热系数;Ts为结构表面温度;Ta为环境温度。
同时,结构会在自然界中通过电磁波向外界发射辐射能,即辐射换热。在实际应用中,辐射换热的热流密度qr可根据黑体辐射定律进行计算[23],即
qr=εC0[(Ts+273.15)4-(Ta+273.15)4]
(10)
式中:ε为结构长波辐射发射率;C0为Stefan-Boltzman常数,为5.67×10-8W/(m2·K4)。
1.2 温差极值估计方法
1.2.1 广义帕累托分布模型
极值分布模型常用于对某一自然事件的尾部数据进行估计,以此推断其极值出现的概率。相较于其他极值分布模型,广义帕累托分布能够充分利用有限的样本数据,在缺少长期监测数据情况下有效描述样本极值段的分布情况。
对于样本数据X={x1,x2,…,xn},在位置参数u的影响下,若样本xi>u,则称yi=xi-u为超出量(i=1,2,…,n)。在假定超出量发生时间服从泊松分布且彼此相互独立的条件下,当给定一个相对大的位置参数时,超出量分布近似服从广义帕累托分布[24],其概率分布函数F(xi,u,k,σ)为
式中:σ为尺度参数;k为形状参数。
依据阈值方法(peakoverthreshold,POT)中的平均剩余图法,计算广义帕累托分布的最优位置参数[19],即
SR(u)=r[E(u)]+std[E(u)]
(13)
式中:E(u)为位置参数u的超出量均值;ny为每年超出量个数;SR(u)为定义的标准残差;r[E(u)]、std[E(u)]分别为使用最小二乘法进行线性拟合下超出量均值的残差与标准差。
对于已知参数分布的广义帕累托分布模型,在采用不同的超越概率p的情况下,分布的极值估计阈值可表示为
式中:xp为超越概率为p时的温差极值估计量;λ=ny/ns,即每年超出量个数ny与年样本个数ns的比值。
1.2.2 竖向温差极值估计流程
考虑实测数据变化的组合梁桥-无砟轨道体系温度场模拟与竖向温差极值估计流程见图2。首先,在单日的温度场模拟时输入逐时变化的环境信息与结构空间位置参数。其次,在太阳辐射计算过程中基于光线追踪法和叉积算法判断结构表面是否受到遮挡[21]。再次,采用1.1节中的方法,分类施加结构表面的太阳辐射、对流换热和辐射换热,计算多种因素共同作用下的无砟轨道-组合梁桥瞬态温度场模型。最后,采用1.2.1节中的广义帕累托分布模型,得到不同超越概率下的竖向温差极值。
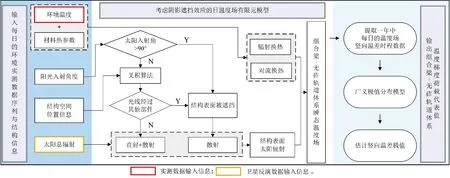
图2 组合梁桥-无砟轨道体系温度场计算与竖向温差极值估计流程图
2 无砟轨道-组合梁桥温度场模型
2.1 工程背景
本文以高海拔大日温差地区某拟建铁路上承式大跨拱桥的拱上连续钢-混凝土组合梁桥与桥面铺设的无砟轨道为研究背景,拱桥立面见图3,拱上组合梁-无砟轨道体系横断面见图4。

图3 某拟建铁路上承式大跨拱桥立面图(单位:cm)

图4 组合梁桥-无砟轨道体系横断面图(单位:mm)
全桥近似为东西走向,位于北纬30.3°,桥面海拔为3 660.55m。钢梁采用Q370ENH钢材,高为2.8m,主梁中心距为4.4m,标准截面为双槽型,支点截面为封闭箱型。混凝土桥面板采用C55混凝土,桥面全宽为11.88m,桥面板标准厚度为30cm,标准翼缘端部厚度为20cm。桥面铺设CRTSⅠ型双块式无砟轨道,结构见图5,板长为6.23m。

图5 CRTSⅠ型双块式无砟轨道结构图
2.2 桥址处实测数据分析
为体现桥址地区气候特点,本文采用桥址地区实测气温数据和卫星反演得到的太阳辐射数据,作为模型中热对流、热辐射边界条件以及太阳辐射热流密度的模拟依据。
桥址处气象观测站建立于2019年底,通过对观测站2020年共2.618×107条温度监测数据进行缺失值、异常值处理,得到桥址处10min平均环境温度数据集,结果见图6。全年最高气温出现在6月22日,单日气温变化为13.3~31.5 ℃;最低气温出现在1月14日,单日气温变化为-11.7~6.0 ℃。桥址地区6月至8月期间的平均温度可达20 ℃,全年最大日温差为20.53 ℃,平均日温差为13.73 ℃,为典型的大日温差地区。
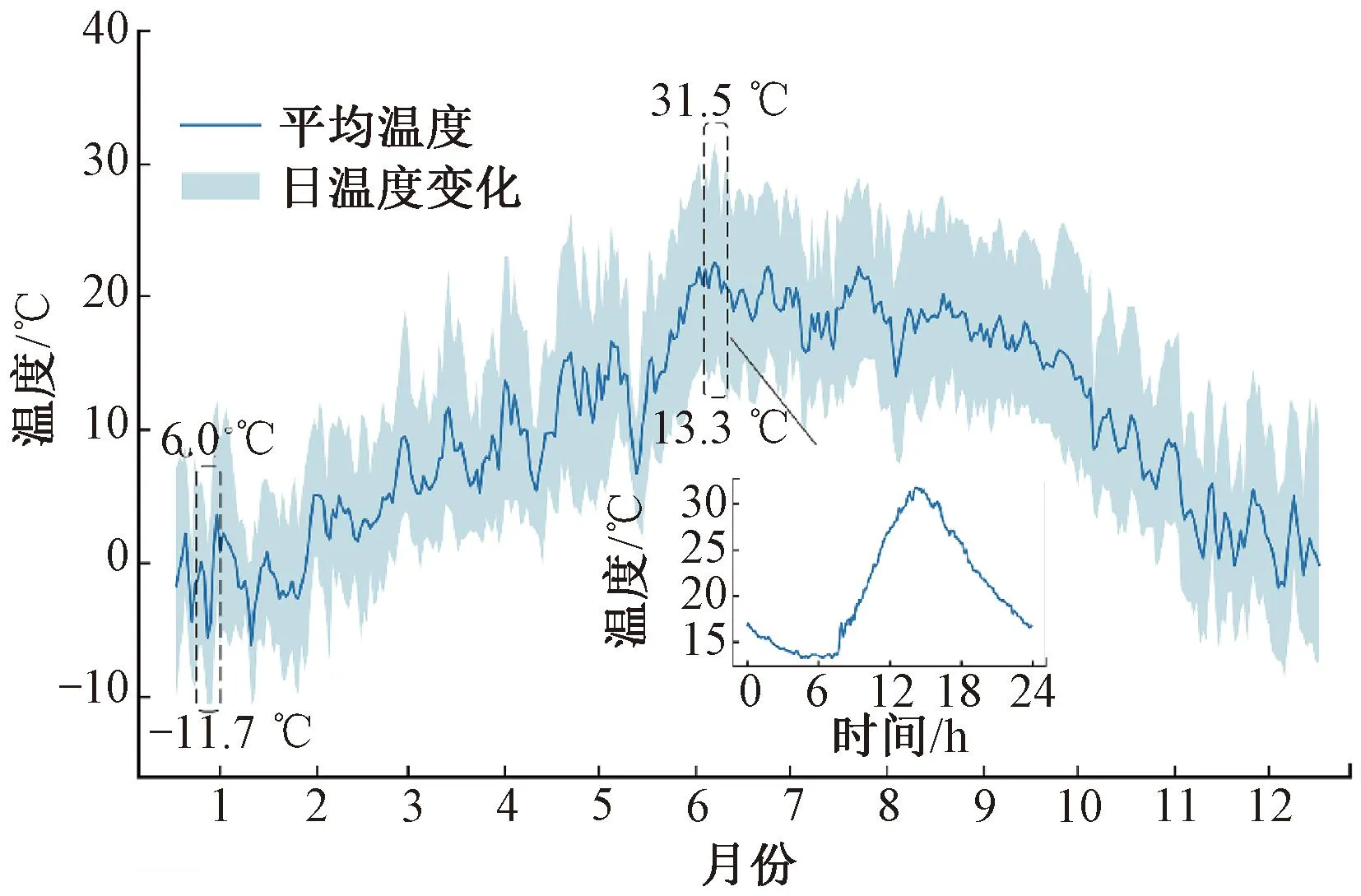
图6 2020年桥址监测点实测日温度变化时程
由于桥址监测站点获取的地表散射辐射的时间精度有限,本文结合高海拔大日温差地区气候特征[10,14],从美国国家航空航天局NASA的MERRA-2数据集(空间分辨率为0.5°×0.625°)获取了晴空指数、散射率和大气上界太阳辐射值[25],根据式(2)计算得到桥址地区每日的逐时太阳辐射强度,典型日期结果见图7。

图7 基于NASA卫星数据的桥址地区典型日期太阳辐射变化
由图7可知,桥址地区大气上界的太阳辐射随季节更替不断变化,夏季最大值超过1 200W/m2,冬季最大值仅为800W/m2。一天中的直射辐射和散射辐射强度随晴空指数和散射率的变化而变化,夏季与冬季的地表水平太阳直射辐射最大值分别达到了800 、600W/m2。桥址地区散射辐射日分布则呈现不规则分布状态,最大值的变化范围在100~400W/m2。相较于平原地区,我国高海拔大温差地区的大气透明度更高,作用于结构的太阳辐射效应更加显著。本文6月21日太阳辐射模型计算结果与文献[10]中同地区辐射对比验证见图8,相同日期太阳直射辐射最大值相对误差为3.3%,可知基于卫星反演方法可以反映该地区地表太阳辐射分布特征。
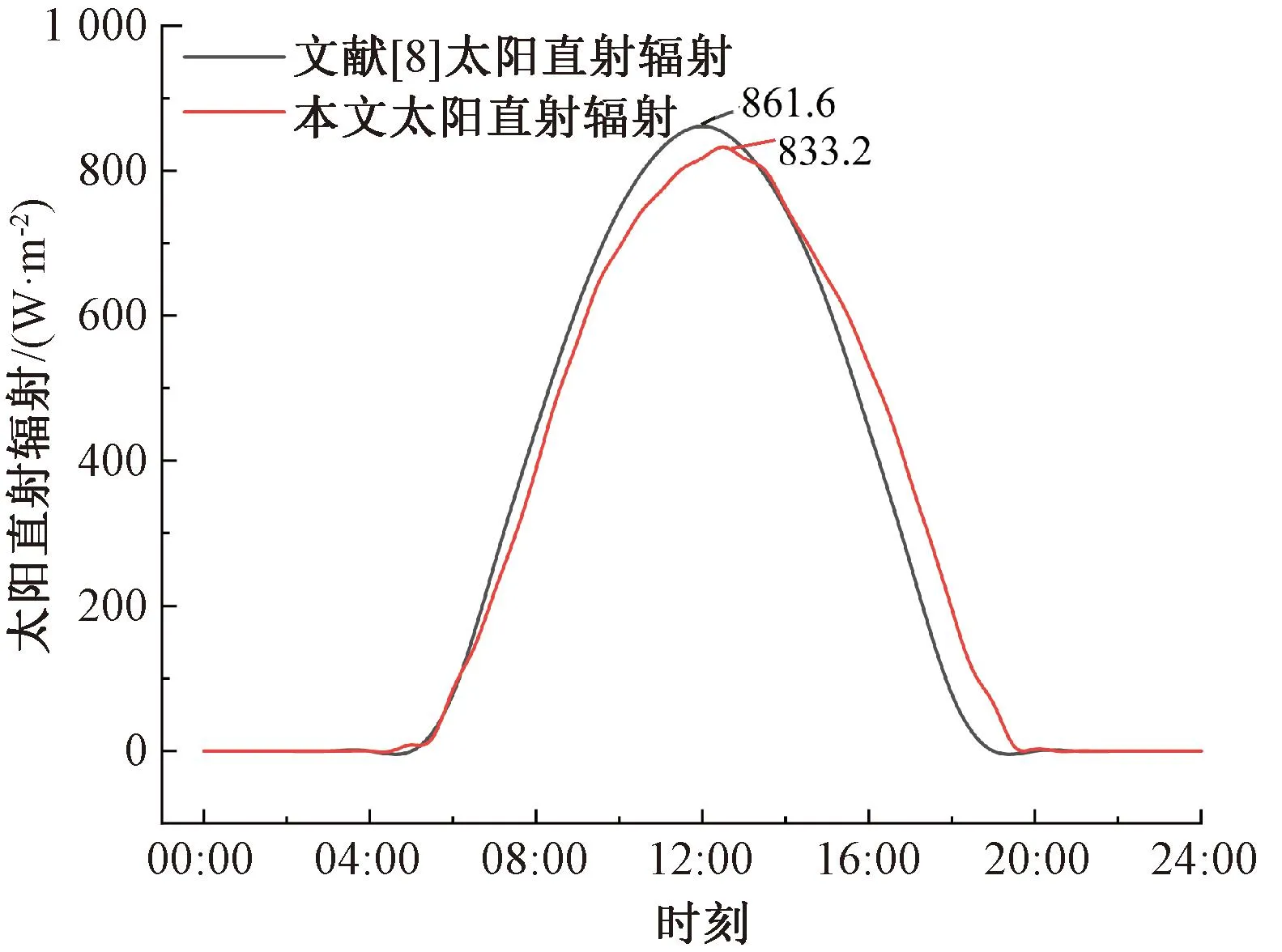
图8 夏季典型日期太阳直射辐射对比验证
2.3 有限元模型计算
2.3.1 模型建立与工况设置
在分析钢-混凝土结合梁的温度场时将剪力栓钉与混凝土桥面板简化为相同温度[6,11]。由于本文仅计算结构温度场,无需考虑温度作用下超静定结构的变形效应,在温度场计算时采用如下假设[26]:
1)组合梁模型沿线路方向采用相同的横截面布置;
2)混凝土板与钢梁之间界面无相对滑移。
基于以上假设,本文建立了与无砟轨道单元板长度相同的6.23 m的组合梁-无砟轨道体系标准截面ABAQUS有限元节段模型,见图9。混凝土桥面板采用传热实体单元DC3D8,钢梁采用传热壳单元DS4。钢梁与桥面板、桥面板与无砟轨道的交界面位置处均采用tie接触条件。
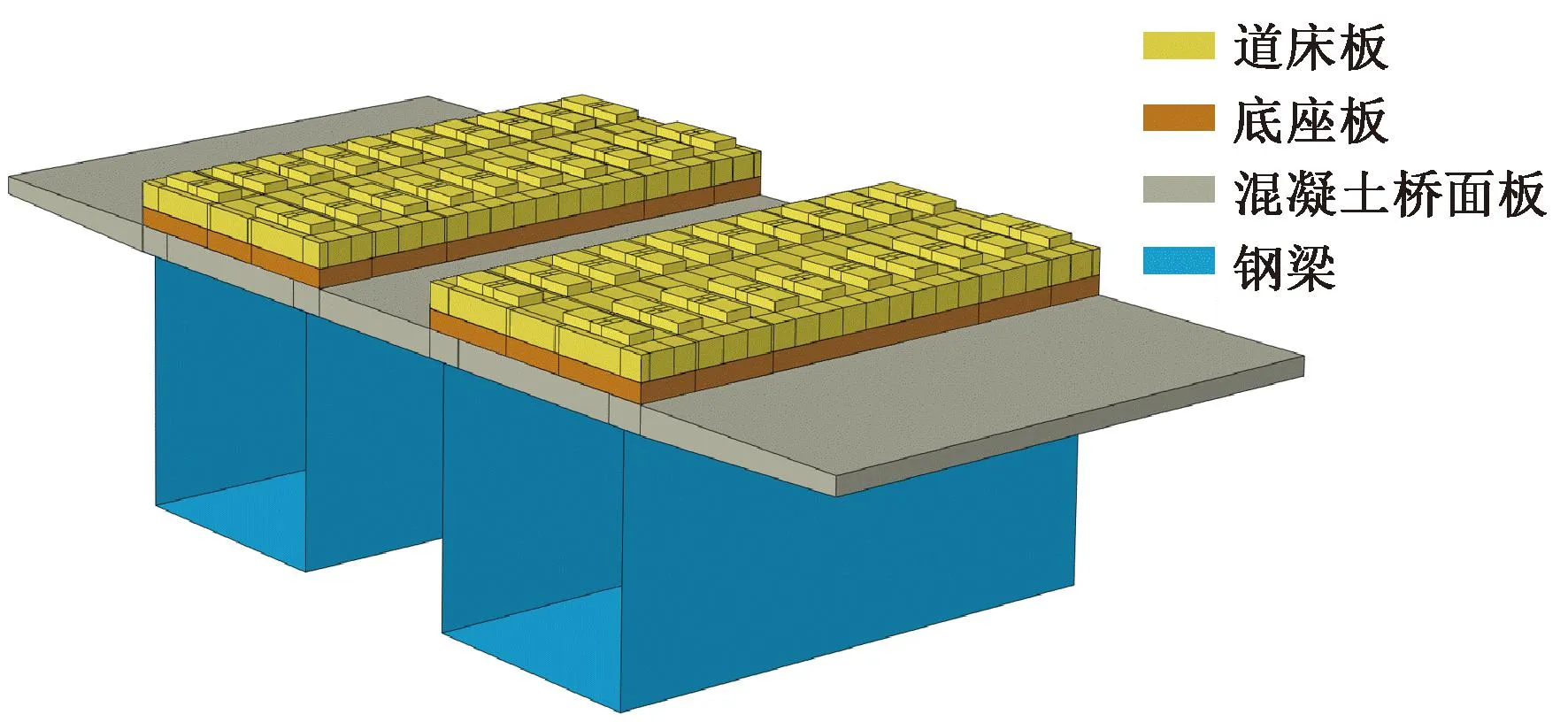
图9 ABAQUS有限元模型图
批量计算了2020年共366 d的日温度场工况,每日的温度场计算按照图2所述的流程展开。单日工况模拟时,进行4个日周期的循环模拟,从而消除初始温度场对日温度场模拟结果的影响。
热边界条件的环境温度采用实测数据输入,太阳辐射值采用卫星反演数据输入。计算共设置192个分析步,单个分析步计算时间为1 800 s,计算步长最小值为1 s,最大值为600 s[6],在每个分析步后更新实测数据输入信息。模型通过python脚本提取模型单元信息及外法线方向信息,采用DFLUX、DFILM子程序实现阴影遮挡区域和对流换热分布的细化。
2.3.2 热参数设置
材料热参数采用文献[2]中的推荐值,见表1。由于本文依托的上承式拱桥的连续组合梁结构距离峡谷底部较远,因此未考虑地面反射对结构日温度场的影响。

表1 材料热参数取值
对流换热系数的取值主要由结构表面粗糙程度、表面相对位置、环境风速等因素决定[6,27],在已知环境温度与结构温度的条件下可通过计算得到。由于本桥尚处于设计施工阶段,在缺乏结构温度实测值或实验测量值参考的情况下,综合考虑学者研究结果及桥梁各表面对流换热系数的差异性[6],采用的对流换热系数见表2。

表2 对流换热系数hc的取值 W/m/℃
2.3.3 温度提取路径
为减少纵向边界条件对模拟结果的影响,采用节段中部截面进行结果采样,并设置温度测点和竖向温度提取路径,见图10。
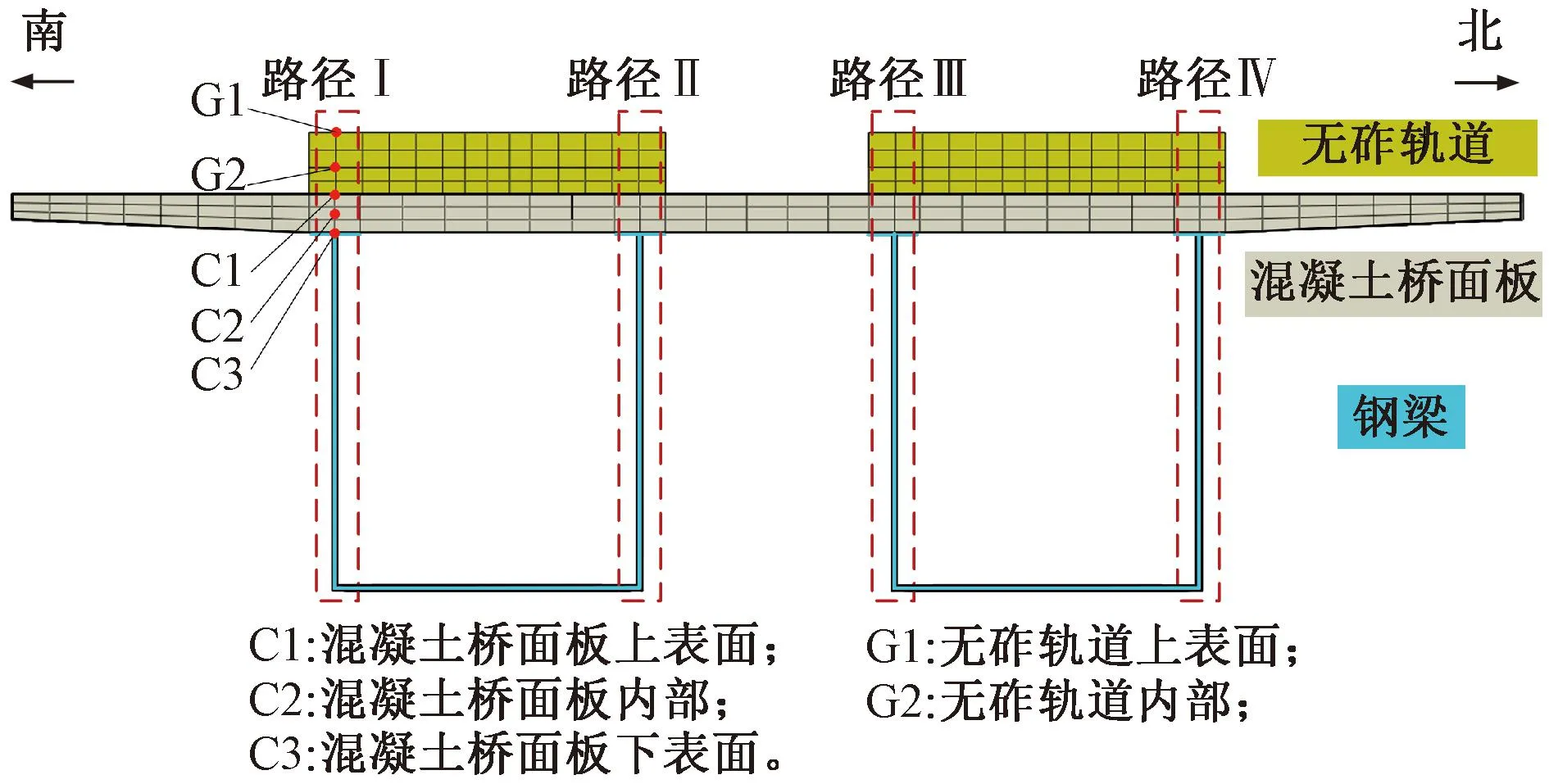
图10 有限元模型温度提取位置分布
2.3.4 温度场模型验证
为验证本文温度场模型的准确性,对比本文与文献[11]中同样位于高海拔大日温差地区的钢-混凝土组合梁桥面板上表面日温度变化,见图11。其中环境温度、太阳辐射以及材料热参数按照文献[11]中取值。
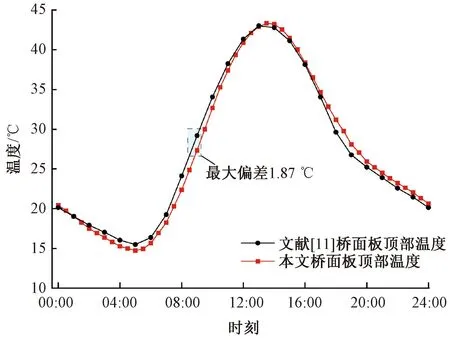
图11 高海拔大日温差地区组合梁桥面板上表面温度对比验证
由图11可知,一天中本文桥面板上表面温度与文献[11]中结果的最大偏差为1.87 ℃,说明本文温度场模型能够准确反映高海拔大日温差地区组合梁结构的温度变化规律。
3 组合梁桥-无砟轨道体系温度分布特征
3.1 体系各季节日温度场变化
以春分、夏至、秋分、冬至日路径Ⅰ的模拟结果为例,分析组合梁桥-无砟轨道体系温度场变化情况,见图12、图13。
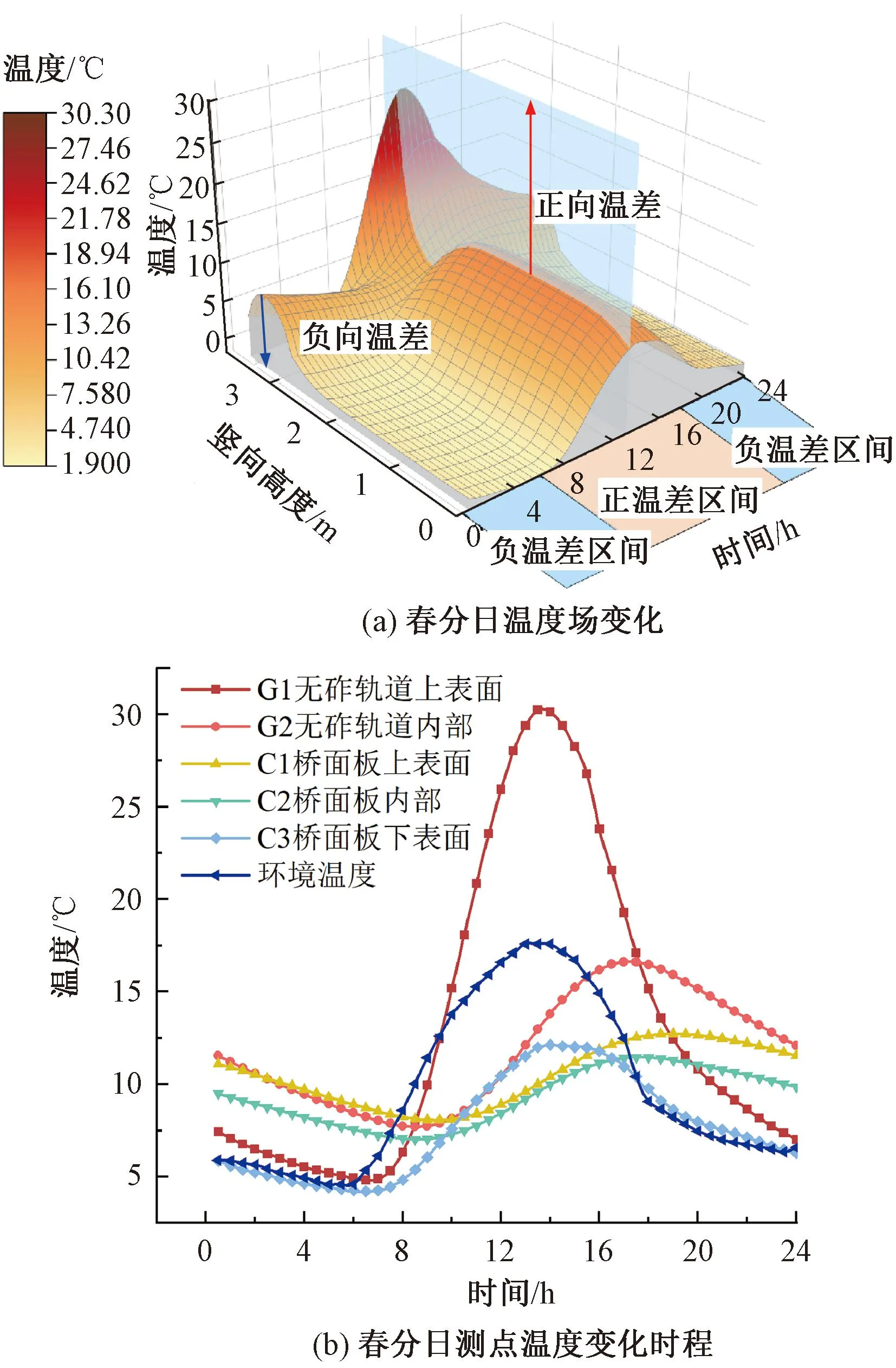
图12 春分日组合梁桥-无砟轨道体系温度变化(路径Ⅰ)
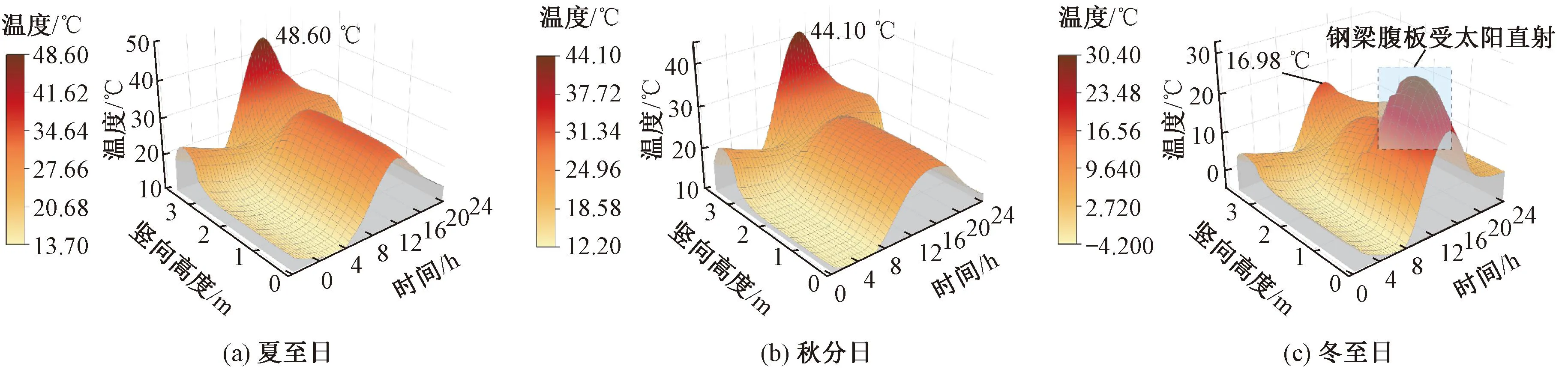
图13 组合梁桥-无砟轨道体系夏季、秋季、冬季典型日期温度场变化(路径Ⅰ)
整体温度变化趋势方面,结合现有研究[2]与图12(a)可知,体系的正、负温差在一天内交替出现。在6:00—18:00时段内,无砟轨道的温度变化幅度较大,温度沿体系的竖向高度从上至下迅速降低,形成正向温差。而在18:00—次日6:00时段内,由于太阳辐射消失和环境温度迅速降低,温度分布转变为混凝土外表面和钢梁位置的温度低,无砟轨道中部位置的温度高,形成负向温差。
由图12(b)可知,无砟轨道上表面G1测点处受太阳辐射影响而波动较大。受混凝土导热性能差的影响,无砟轨道内部G2、桥面板各个位置的温度波动幅度均小于环境温度,温度变化也滞后于环境温度。夜间无砟轨道上表面与桥面板下表面与环境温度趋于一致,内部温度的降低速度仍具有滞后性。
综合图12、图13可知,受到环境温度和太阳辐射的影响,各个季节体系竖向正温差均在13:00—14:00之间达到最大值,夏至日无砟轨道上表面的最高温度可达48.6 ℃;各季节在夜间的竖向负温差变化较为平缓,在22:00—2:00之间达到最大值。
由图12和图13(a)、13(b)可知,由于钢材导热性能优异,在春、夏、秋季,钢梁腹板的沿竖向高度的温度分布基本相同。而由图13(c)可知,在冬季时,组合梁南侧的钢梁外腹板温度在太阳直射辐射的影响下沿竖向高度波动更大,钢梁最高温度可达30.4 ℃。
3.2 阴影遮挡效应对体系温度场的影响
钢梁外腹板受翼缘板遮挡效应的年变化规律见图14。在太阳辐射作用最大的正午12时,受到太阳高度角的变化以及翼缘板的遮蔽作用,组合梁南侧的外腹板只有在冬季时才能受到太阳直射作用,腹板的太阳直射区域高度在冬至日时达到103.6 cm的最大值。
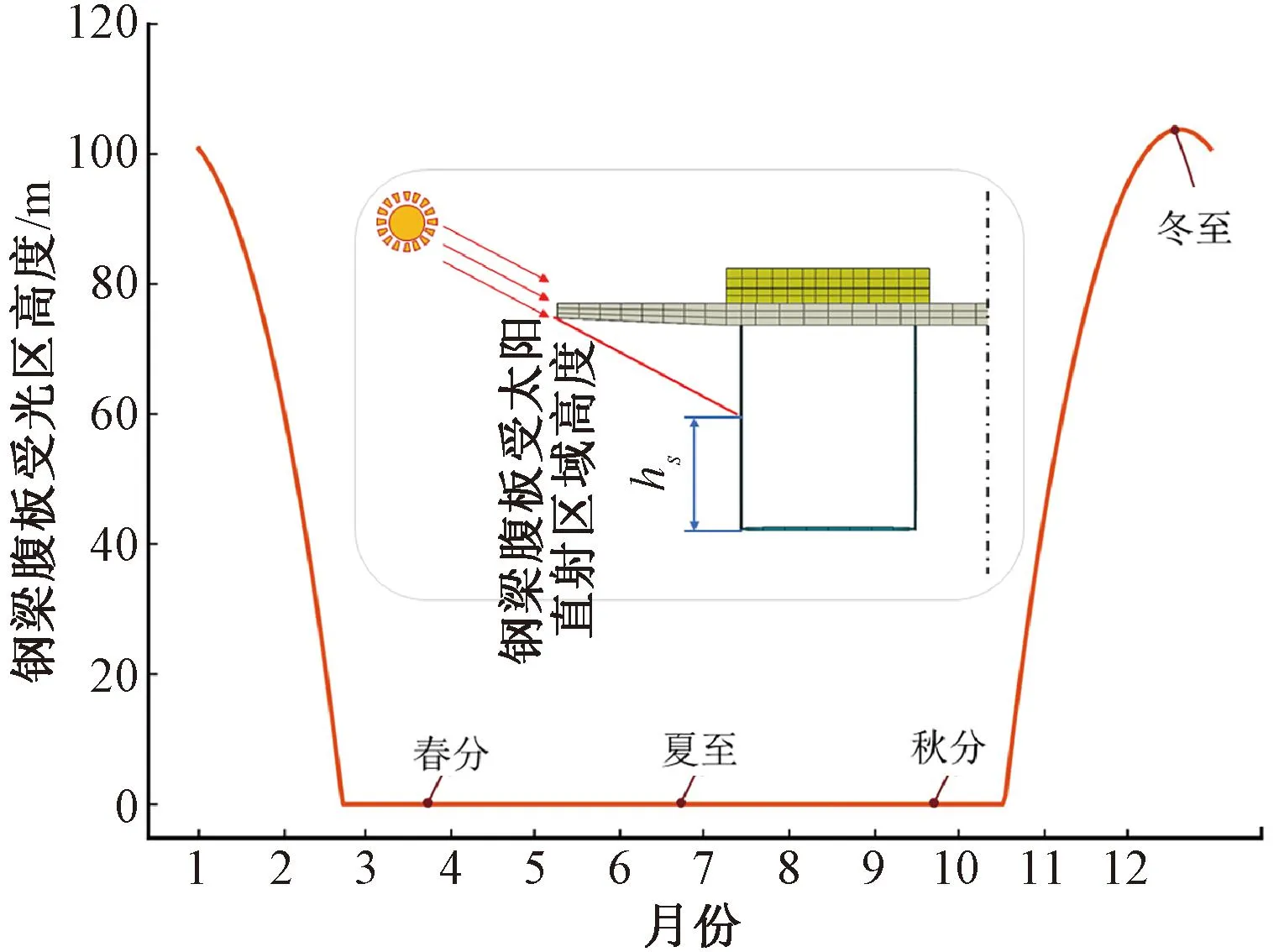
图14 正午12时南侧腹板受太阳直射区域高度时程
进一步研究夏至日混凝土桥面板上表面在典型时间段的温度对比,见图15。结果表明,桥面板上表面受无砟轨道遮挡影响出现横向温度分布不均匀效应,横向温度呈现“凹”型分布规律。在14:00时,桥面板横向最大温差达到了22.3 ℃。
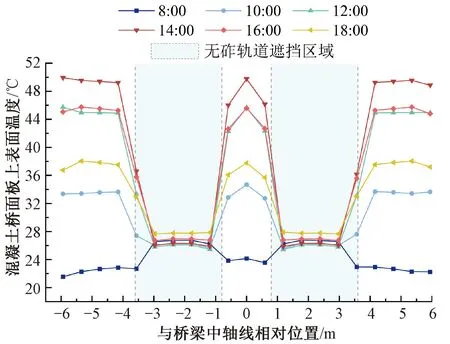
图15 夏至日桥面板上表面典型时刻横向温度分布图
3.3 体系竖向温差分布特征
实际工程设计中更关注结构竖向温差的空间分布特征。为比较不同季节、不同温度提取路径的组合梁桥-无砟轨道体系的竖向温差分布特点,以四季典型日期在14:00、22:00时温度提取路径Ⅰ、Ⅱ的模拟结果为例,分析体系的竖向温差分布特征,见图16、图17。

图16 组合梁桥-无砟轨道体系各季节竖向正温差分布图(14:00时)
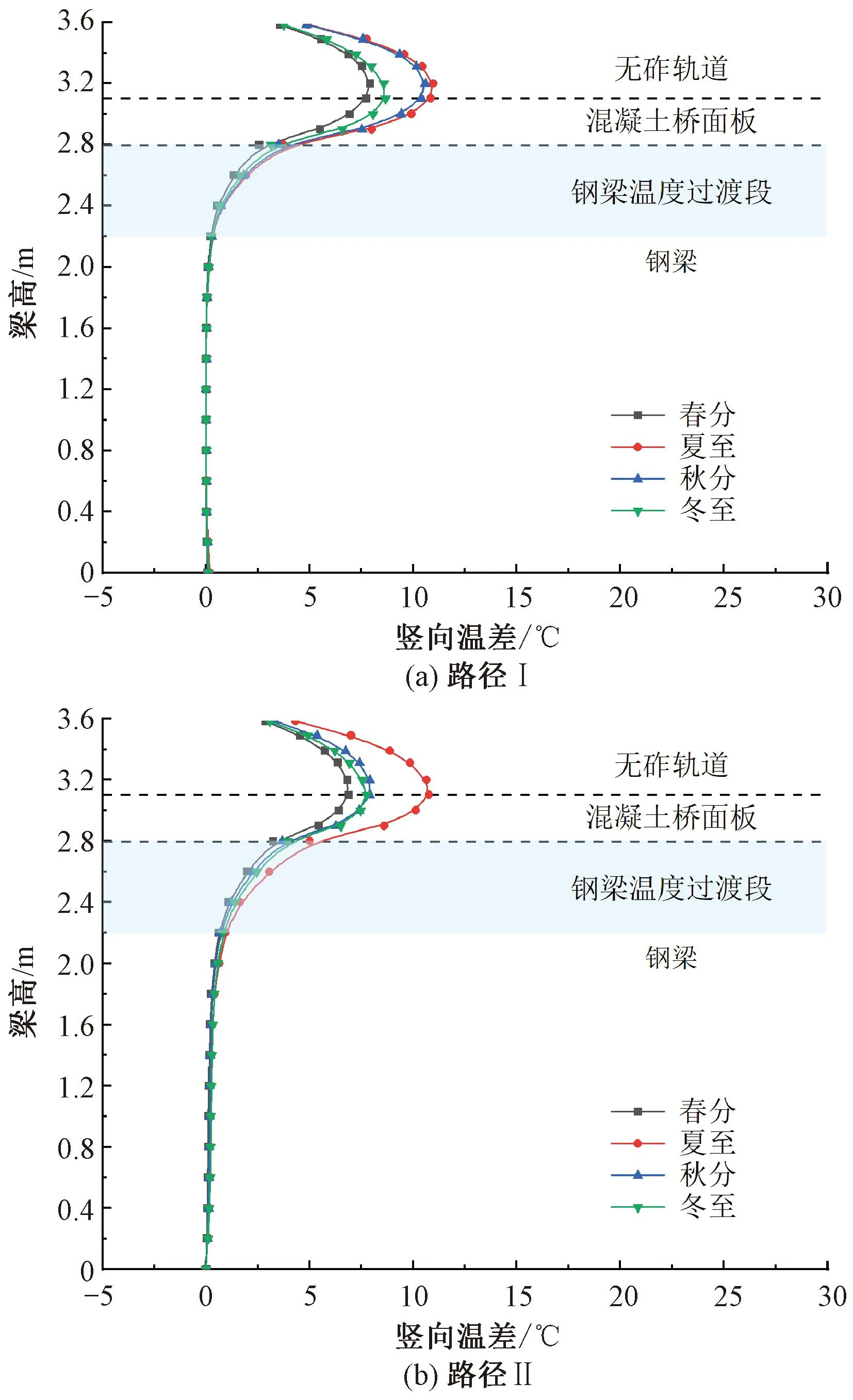
图17 组合梁桥-无砟轨道体系各季节竖向负温差分布图(22:00时)
正温差分布方面,由图16可知,无砟轨道顶部在夏至日的最大正温差可达25 ℃。不同季节的竖向正温差在无砟轨道范围内的斜率变化最大,而在混凝土桥面板范围内处于最低值。
特别地,钢梁局部的竖向正温差最大值出现在路径Ⅰ中冬至日外侧钢梁腹板受太阳直射区域。由于冬季无砟轨道上表面受到的太阳辐射作用减弱,路径Ⅱ中的内侧钢梁在冬至日时的局部竖向正温差最大,此时体系整体的竖向正温差最小。
负温差分布方面,由图17可知,竖向负温差的最大值出现在无砟轨道的底部区域,夏至日的最大竖向负温差可达10 ℃。不同季节、不同路径的竖向负温差分布趋势相同,在内外侧钢梁腹板位置均处于最低值。
竖向温差分布在不同高度处的斜率拐点可以作为典型的竖向温差分布特征。分析图16和图17可知,竖向温差在无砟轨道区域内的斜率拐点距离顶部约为0.3 m,约占无砟轨道高度的3/5。钢梁与混凝土桥面板连接的钢梁顶部形成了温度过渡段,钢梁温度过渡段的高度约为0.6 m,约占钢梁高度的1/5。
根据图16、图17中最不利竖向温差分布特点,参考欧洲规范[28]对组合梁桥温度梯度模式的相关规定和现有文献[6-7,10],本文提出多折线形式的组合梁桥-无砟轨道体系竖向温度梯度模式,以此作为后续竖向温差极值估计的依据,见图18。

图18 组合梁桥-无砟轨道体系竖向温度梯度模式
图18中,H为钢-混凝土组合梁高度,hw为无砟轨道高度,hc为混凝土桥面板高度,hs为钢梁高度。考虑钢梁腹板因太阳直射而产生的内外侧温差,在正温度梯度模式中,温度梯度代表值T′3仅采用南侧受光腹板提取路径Ⅰ的结果,其他代表值采用路径Ⅱ、Ⅲ、Ⅳ的平均值。在负温度梯度模式中,因为夜间钢梁腹板温度与环境温度趋于一致,所以代表值采用4条路径的平均值。
3.4 基于广义帕累托分布的竖向温度梯度拟定
本节基于3.2节中得到的竖向温度梯度模式,采用1.2.1节的广义帕累托分布方法,对全年日温度场模拟得到的竖向温差样本数据进行统计分析,建立温差极值的渐进分布模型,最终得到在不同超越概率下的竖向温差阈值。
以正温度梯度中竖向温差T1为例,首先,将每日温度场模拟过程分为正温度梯度过程(6:00—18:00)和负温度梯度过程(18:00—次日6:00),将各时刻的温差数据作为统计总体,并将每日的极值数据作为样本,以此消除日温度场相关性的影响。其次,对分布的位置参数进行优选,采用式(12)、式(13)计算平均超出量与标准残差,见图19。

图19 升温过程T1温差平均超出量与标准残差随广义帕累托分布位置参数变化曲线
由图19可知,当位置参数过小时,分布的拟合效果不佳;而当位置参数过大时,样本中的超出量个数减少,分布拟合的误差增大。图示升温过程T1温差的优选位置参数区域在23.5~24.5 ℃之间,由此选择标准残差最小的24.18 ℃作为最优位置参数。
在确定最优位置参数后,采用极大似然估计得到分布的尺度参数和形状参数,得到温差极值区域的概率分布拟合结果,见图20。由图20可知,样本累积概率与GPD估计累积概率拟合较好,能够反映温差样本在极值区域的分布情况。
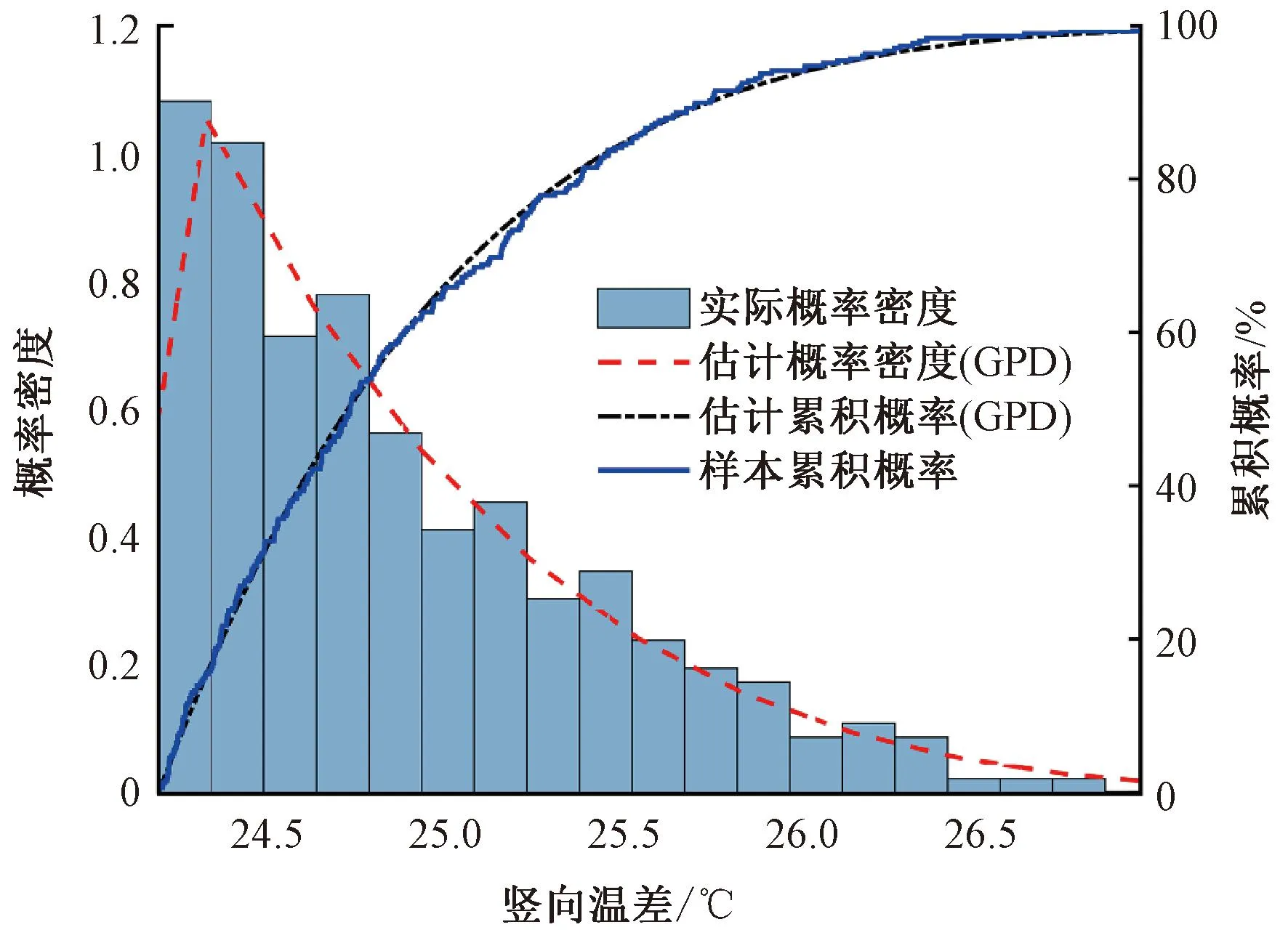
图20 升温过程T1极值温差的广义帕累托估计
依据GB50216—2019《铁路工程结构可靠度设计统一标准》[29],温度作用的代表值可采用其设计基准期内极大值概率分布的某一分位值。采用上述流程和式(13),得到图19中不同位置处的竖向温度梯度作用代表值估计结果(负温度梯度的代表值取相反数计算),见表3。由表3可知,冬季与其余季节的外侧钢梁腹板温差代表值差异(T′3-T3)可达15.38 ℃,表明阴影遮挡效应对钢梁腹板的局部温差影响显著。

表3 竖向温度梯度代表值估计
3.5 高海拔大温差地区与平原地区温度梯度对比分析
将本文归纳的竖向温度梯度与文献[7]提出的平原地区的钢-混凝土组合梁桥竖向温度梯度回归公式进行对比分析(公式中代入本文结构参数)。参考欧洲规范对于温度作用取值的确定方法[28],使用年超越概率为0.02的竖向温度梯度代表值作为本文拟定的温度梯度作用设计值,对比结果见图21。
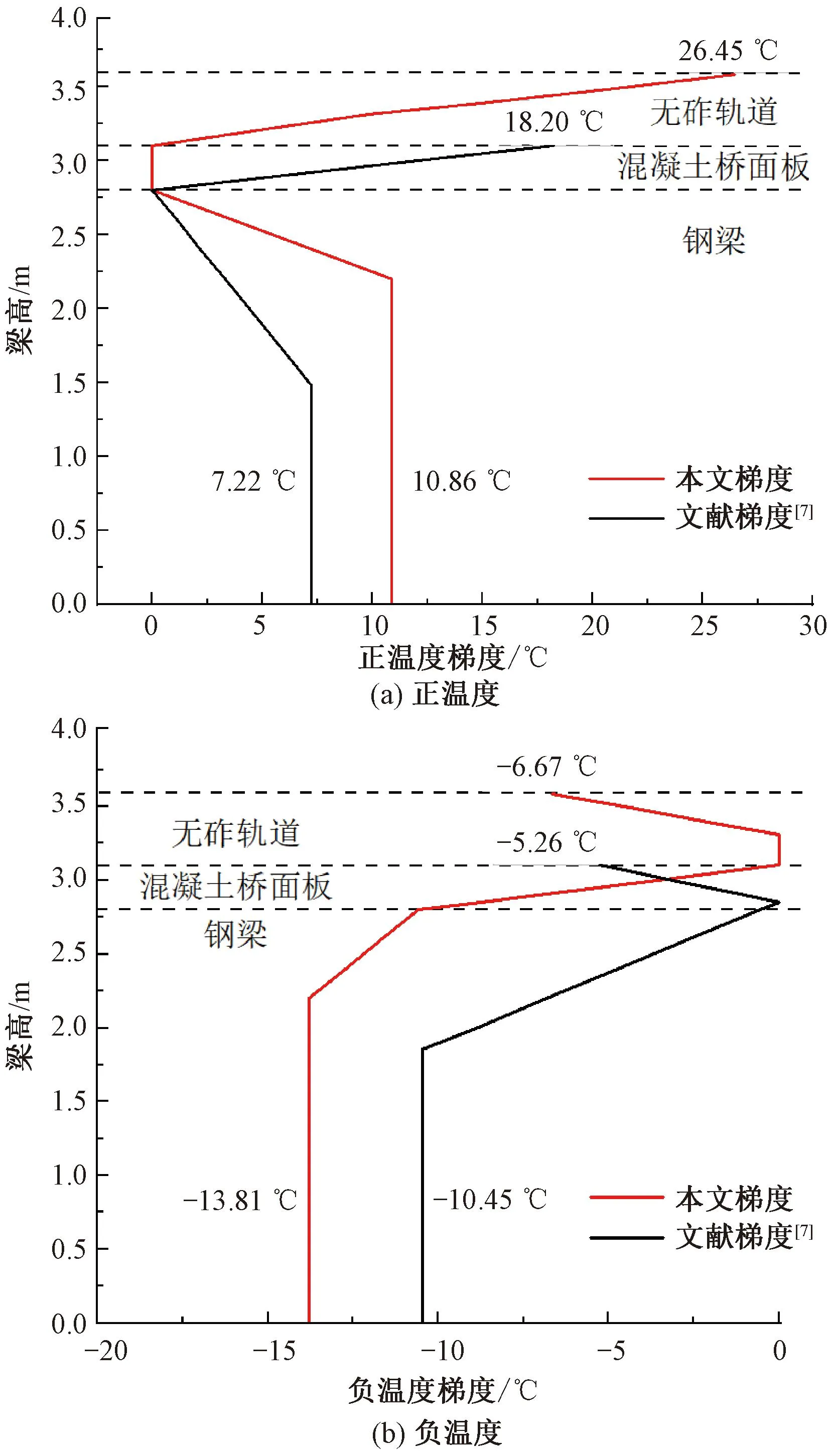
图21 本文梯度与平原地区温度梯度对比
由图21可知,温度梯度极值方面,受强太阳辐射和日温差变化大的影响,高海拔大日温差竖向各位置处的温度梯度极值均高于平原地区。竖向温度梯度分布规律方面,本文钢梁温度过渡段高度小于文献中的结果;由于无砟轨道厚度大于组合梁桥面板厚度,相较于独立的组合梁温度梯度,体系温度梯度曲线整体向上偏移。无砟轨道对于桥面板竖向正温梯度的折减效应显著,并且改变了桥面板负温度梯度的梯度方向。
4 结论
本文以我国高海拔大日温差地区组合梁桥-无砟轨道体系为研究对象,基于实测环境数据建立了考虑阴影遮挡效应与逐时边界条件更新的温度场模型,描述了该地区组合梁桥-无砟轨道体系在日间升温和夜间降温两种模式下的温差分布特征,归纳了温度场的变化规律和最不利竖向温差分布规律。进一步基于多折线形式的竖向梯度模式与极值估计方法,得到了不同超越概率下的温度梯度代表值。主要结论如下:
1)体系竖向正温差的极值出现在13:00至14:00,竖向负温差极值出现时间在22:00至次日2:00。无砟轨道-桥面板区域的温差极值均出现在夏季,钢梁顶部存在与桥面板的温度过渡段,钢梁温差极值出现在冬季受太阳直射影响的南方外侧腹板区域,桥面板上表面受无砟轨道遮挡影响日间横向温度呈“凹”型分布。
2)本文得到的竖向正温度梯度在无砟轨道顶面处的最大值为26.45 ℃,考虑冬季太阳直射影响的钢梁腹板局部正温度梯度最大值为26.48 ℃;竖向负温度梯度最大值为-13.81 ℃。相较于单独的组合梁梯度,体系整体的温度梯度曲线上移,梯度在无砟轨道区域距离顶面3/5轨道高度范围内迅速降低。
3)本文提出的考虑实测环境温度与太阳辐射随机变化的参数化有限元分析方法为拟合组合梁桥-无砟轨道体系温差极值分布创造了良好的统计数据基础,可为本地区桥-轨设计阶段温度梯度值的计算提供参考。
4)随着桥址处监测数据不断更新,可以基于新获取的数据对本文提出的竖向温度梯度进行检验和修正,并进一步开展桥址处多种气象监测数据与结构温度场之间的相关性研究。

