微透镜阵列成像串扰现象分析

张 玉，李武军，焦文龙，郭苗迪

(西安工业大学 基础学院,西安 710021)

微透镜是一种常见的微光学元件,把一系列微透镜规则排列起来就是微透镜阵列[1],作为一种精密光学元器件,它可以在微光学角度实现光的传输、变换、成像等功能,同时具有视角大、像差小、畸变小、时间分辨率高等优点[2],被广泛应用于自适应光学、光信息处理、增强现实和高灵敏度成像等领域[3-4]。使用微透镜阵列较多的领域之一是集成成像,这种成像方式不需要佩戴设备就能观看全视差、彩色、视点无跳变的三维场景,也不需要相干光源[5-8]。相比传统成像,集成成像最突出的优点在于通过一次成像,不仅能够在像面上记录二维位置信息,还能获取不同光线的角度信息和物方的深度信息。经微透镜阵列聚焦后所成的单元图像,对于常用的探测器件(CCD和CMOS)来说,其占有的像元数目反映微透镜阵列成像的空间分辨率,这也直接决定深度分辨率[9],从而影响整体的成像质量。受到阵列自身结构和成像系统的参数限制,可能在像面上出现两种情况,其一是单元图像产生串扰现象,该现象极大的降低微透镜阵列成像的空间分辨率;其二是单元图像分离的较远,此时单元成像面积减小,单元图像占有的像元数目减少,这就会造成探测器件像元的浪费。

针对成像串扰问题,从微透镜阵列成像提出以来发展至今,使用较多的是利用周期性的黑色掩膜消除串扰,但这种方式存在光线利用低的问题,极大地损失了光能量。基于上述原因,文献[10]在2组相邻图像元的位置添加了呈正交排列的偏振片阵列,用于阻挡相邻图像元的串扰光线。文献[11]优化了传统的透镜阵列,采用非球面的微透镜阵列获得了小于0.2低串扰的效果,最终实现桌面自动立体显示。文献[12-13]提出在显示器和微透镜阵列之间插入孔径阵列,孔径阵列中的微孔阻止相邻单元图像的小角度串扰进入阵列中相应的小透镜。文献[14]通过特定参数设计的掩膜板阵列,有效地阻挡了相邻图像元间的光线,消除了视区串扰现象。上述文献均采用在系统中加入阵列结构的方式,阻挡相邻图像元的光线,难免存在器件结构复杂、不易于量产化的问题,同时未考虑到成像系统的参数对图像串扰的影响,无法分析系统的最佳设计参数。本文拟从成像系统的各参数出发,包括微透镜阵列的结构参数和目标物的参数,探讨影响成像空间分辨率的因素,分析调整各参数对单元图像间距的影响,给出避免单元图像产生串扰现象的临界参数,从而提高整体系统的成像质量。

1 微透镜阵列的单元透镜成像特性

对于单元透镜光轴平行的微透镜阵列而言,由于各项参数均相同,将单元透镜的成像过程看作二维并行光路,其光线传输、变换的功能与分立的单透镜相同,不同之处在于单元透镜的空间位置不在微透镜阵列的主光轴上,因此,本文通过物面和像面的坐标变换,分析光线通过任意透镜的变换特性,最终得到微透镜阵列的光学成像性质。

取微透镜阵列的坐标系如图1所示,阵列主光轴z通过阵列中心,单元透镜光轴与主光轴平行,用zi表示,o-x-y和o′-x′-y′分别表示物面和像面,yp1和yp2分别表示透镜阵列的前端面和后端面。

图1 微透镜阵列的坐标系

为了便于研究,取单元透镜的成像关系如图2所示。

图2 单元透镜的成像关系

根据矩阵光学理论,对于一个单元透镜而言,系统的成像矩阵可以表示为

(1)

式中:f为单透镜的焦距,l1和l2分别为物距和像距。根据成像条件存在

(2)

联立式(1)、(2)可得成像系统的放大率为

(3)

阵列主坐标系与单元透镜坐标系之间存在

x=xi+εi

y=yj+υj,

(4)

(5)

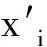
(6)

对于一个有m×n个单元透镜的阵列而言,设两相邻透镜在x和y方向上的中心间距为d,则第(i,j)(i=1,2,3,…,m;j=1,2,3,…n)个微透镜的中心坐标(εi,υj)可以写成

εi=id

υj=jd,

(7)

根据式(4)、式(5)、式(6)可以得到,单元透镜在阵列主坐标系下,像面与物面间的关系满足

x′=Mx+id(1-M)

y′=My+jd(1-M),

(8)

从式(8)可以看出,每一个单元透镜所成图像对应于同一像面上的一个单元图像,单元图像大小相等且相距一定距离,这就是微透镜阵列的单元透镜成像特性。进一步分析可以得出:单元图像在像面上的分布与单元透镜的中心间隔d和放大率M有关,由式(3)可知透镜焦距f和像距l2决定成像放大率M,式(2)给出了清晰成像时物距l1、焦距f和像距l2的关系,也表明焦距f和物距l1决定着成像的放大率M,从而影响像面上的单元图像分布。

2 清晰成像的临界参数分析

2.1 微透镜阵列成像的模拟计算

通过上述对微透镜阵列单元透镜成像特性的分析,根据单元透镜在阵列坐标系下像面与物面间的关系,采用Matlab软件设计程序,模拟计算讨论成像系统中各参数对单元透镜成像的影响。

模拟计算时,取2×2的微透镜阵列进行计算,其中单元透镜阵列正方形紧密排列。物面选取的尺寸为50 mm×50 mm,像素为1 080×1 080。模拟计算得到不同参数下,对应像面上的模拟计算结果如图3所示。其中图3(a)给出的是单元图像出现串扰的情况;图3(b)给出的是各单元图像恰好不产生串扰的情况,即临界情况;图3(c)给出的是各单元图像出现分离的情况。

图3 模拟计算的像面情况

2.2 成像系统的参数对串扰的影响

固定单元透镜中心间距d为10 mm,透镜阵列以正方形紧密排列,取物距l1为50 mm,物面为图3.1中尺寸的物面图像,模拟计算得到的边缘距离b随焦距f的变化情况如图4(a)所示;固定透镜焦距f为5 mm,物距l1为50 mm,对上述同样的物面图像,计算边缘距离b随间距d的变化情况如图4(b)所示;固定单元透镜间距d为10 mm,焦距f为5 mm,物距l1为50 mm,计算获得的边缘距离b随物面尺寸L的变化情况如图4(c)所示;固定单元透镜间距d为10 mm,焦距为5 mm,物面尺寸L为50 mm×50 mm,得到的边缘距离b随物距l1的变化情况如图4(d)所示。

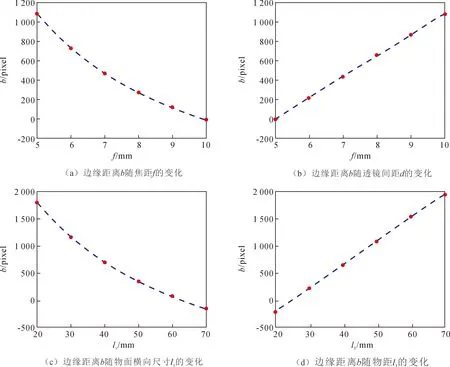
图4 不同参数值下单元图像的边缘距离

从图4(a)可以看出,焦距对单元图像分布的影响是非线性的,b随f的增大而减小,当f较小时,b减小得较快,而f较大时,b减小得慢。对所使用的模拟计算参数,当单元透镜的f为10 mm时,b为0,此时,单元图像恰好不产生串扰。由此可见,当其他参数固定时,选用短焦距的微透镜阵列有利于避免单元图像产生串扰现象。

从图4(b)可以看出,单元透镜的间距对单元图像分布的影响呈线性关系,即随着d增大,b逐渐增大,在选定的参数情况下,当d为5 mm时,单元图像恰好分离,据此,增大单元透镜的间距是提高成像分辨率的有效途径。

为了便于研究,假定仅考虑一维的横向尺寸Lx,从图4(c)可以看出,b随Lx的增大而减小,在选定的参数情况下,当Lx为100 mm时,单元图像恰好不产生串扰。在临界值以内,Lx越小,b增加得越快。据此,减小物面尺寸可避免单元图像间产生串扰。

从图4(d)可以看出,随着l1的增大,b线性增大;且当l1为23 mm,b为0,表明此时单元图像恰好不产生串扰。据此,在其他参数一定时,适当增大物距可以有效避免单元图像间的串扰 。

2.3 临界参数测量实验

采用焦距为7 mm,直径为9 mm的两块微透镜,制作成1×2的微透镜阵列。设计光路如图5所示,实验测量清晰成像的临界参数,选取尺寸为55 mm×55 mm×55 mm的魔方作为成像物,用其中的一个面作为物面进行成像。LED光源发出的白光经物面反射,光线通过微透镜阵列的单元透镜成像在像面上。

图5 微透镜阵列成像的临界参数的实验测量图

分别移动微透镜阵列的位置,即改变物距,并在透镜后方移动像面的位置,寻找成清晰像时,两个单元图像边缘恰好分离的位置,获得的像面图像如图6所示,测量得出当物距为40 mm、像距为8.5 mm时,单元透镜成清晰像且恰好分离。

图6 单元图像恰好分离的实验结果

根据式(2),对于焦距为7 mm的透镜,物距为40 mm,当物面尺寸为55 mm×55 mm时,理论计算给出的像距为8.48 mm,由模拟计算的结果得出,当要成清晰像,单元图像恰好不产生串扰时,单元透镜中心间距的理论值为9.62 mm。对比实验测量方法和结果,表明理论模拟计算值与实验测量结果基本一致。由图6可以看出,实验中采用焦距为7 mm的微透镜,单元图像均存在桶形畸变[15],这是由于随着视场角的增大,透镜各部分的折射作用不同而引起同一色光的像差现象,表现为对同一距离的物体的不同部分的放大率不同而产生变形[16-17]。这种现象不会影响像面的清晰程度,但会影响成像位置的精度,给实验带来误差,并且在两微透镜中心连线上,该畸变产生的误差最小。

3 结 论

针对光学成像系统中的微透镜阵列,根据矩阵光学理论分析微透镜阵列成像的物面与像面关系,并进一步采用数值模拟的计算方法,分析单元图像间距随成像系统各参数的变化规律,得出了清晰成像的临界参数。

通过分析微透镜阵列成像时系统参数、物面尺寸与成清晰像时单元图像间距的关系,计算得出,第一,单元图像间距随透镜焦距和物面尺寸的增大而减小,且该变化规律呈现一定的非线性关系;第二,单元图像的间距随微透镜阵列间距和物距的增加而线性的增大。最后通过设计的1×2的一维透镜阵列进行实验成像,成像结果与理论分析结果一致。结果表明,当采用微透镜阵列成像时,对确定的物面尺寸,减小透镜焦距,增大透镜间距,或增大物距能有效提高单元图像的间距,能够避免单元图像间产生串扰,提高成像分辨率。该结果对设计微透镜阵列的成像系统具有一定的参考价值。