高层六边形网筒结构变形转角计算方法
符子欣,李志军,汤若辰
(西安工业大学 建筑工程学院,西安 710021)
六边形网筒结构的外框筒立面形式是参照自然界中蜂巢的几何形状提出的,高层六边形网筒结构立面形式中没有传统的垂直柱,是通过六边形网格单元围绕在整个建筑周边形成外框筒,并将其转化为斜柱的轴向拉压应力向下层传递,从而抵抗重力、剪切和弯曲作用,具有强大的抗侧向刚度[1]。六边形网筒结构是在斜交网筒结构的基础上进行创新改进而来,目前该结构体系在世界各地已经拥有较少工程的实际应用[2-4],例如中钢国际广场,巴哈尔塔、广州西塔项目等[5]。
为了深入了解网筒结构的受力性能和抗振机理,文献[6-7]对外框筒立面中斜柱角度为变角度的斜交网格筒结构进行了分析,得出当高宽比不大于7时,采用统一角度的斜柱立面形式比变角度的更加经济适用的结论,但未具体分析斜柱角度的变化对结构抗震性能的影响,得出最优角度区间。文献[8]首次基于六边形网格筒结构的力学性能来评估其在高层建筑中的适用性,得出几何参数变化对整体结构性能的影响较为明显,通过改变结构的主要几何参数,评价了几种高层建筑实例的结构方案。文献[9-11]基于推覆和增量动力分析分别研究了33、45和53层三种不同斜柱角度的六边形网筒结构的抗震性能,并在此过程中分析了结构连续抗倒塌性能。目前研究仅分析杆件几何因素对抗侧刚度的影响,对六边形网筒结构进行抗震分析时完全依赖有限元软件,未提出一套变形转角的简化计算方法。文献[12]根据结构斜交网筒结构层间位移确定抗震性能水平划分标准,给出了结构和非结构构件损伤情况与层间位移角的对应关系,文献[13-14]确定了斜交网筒结构抗震性能水平相对应的层间位移角,地震耗能过程主要靠外筒斜柱和内筒联系梁。
层间位移角是反映结构抗侧向刚度和变形能力的重要指标,目前规范对六边形网筒结构的层间位移角限值没有明确规定。因此建立六边形网筒结构变形转角的计算公式,研究不同斜柱角度结构的层间位移角限值对该结构合理的抗震设计有重要意义。本文拟通过考虑结构弯曲变形和剪切变形的影响,推导剪切刚度和弯曲刚度的简化计算式,基于结构腹板角部斜柱的轴向应变与子模块变形转角之间的关系建立六边形网筒结构的结构子模块变形转角计算式,并与有限元模型计算结果进行分析比较。
1 六边形网筒结构的构建
如图1所示,六边形网筒结构是将六节点的六边形网格单元围绕在整个建筑周边形成外框筒,以抵抗重力和侧向荷载。
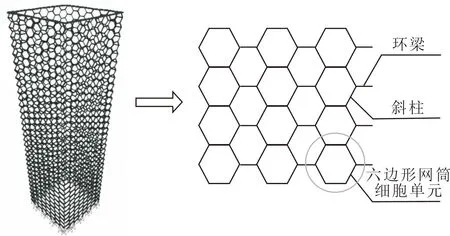
图1 六边形网格筒结构立面示意图
六边形网格单元又可以细分为两种类型:由四个斜柱和两个水平梁组成的水平六边形网格,以及由四个斜柱和两个垂直柱组成的垂直六边形网格。与斜交网格筒结构最大的区别,就是六边形网格筒结构在立面形式中以六边形网格的单元代替了斜柱与水平环梁交叉所组成的稳定“三角形”。六边形网格单元中的斜柱以轴力的形式从上向下传递,从而抵抗重力、剪切和弯曲作用。
文献[15]指出随着建筑高度的增加,斜交网格外筒对整个结构体系抗侧刚度的贡献也逐渐增大,同时内筒剪力墙的抗侧负担也被减轻。文献[16]中指出在六边形网格筒结构中,内部核心筒的侧向刚度仅占结构总侧向刚度的20%~30%。而作为主要抗侧移构件的六边形外框筒,由于斜柱角度对其抗震性能影响较大,且内部核心筒通常仅仅被作为承重构件。
2 变形转角计算
2.1 典型六边形细胞单元剪切刚度简化计算
基于刚性楼板假定,高层六边形网格筒结构外框筒六边形细胞单元在层间剪力作用下的受力分析及变形简化如图2所示。

图2 六边形斜柱单元变形简图
假设构件只承受轴向力,则斜柱抵抗的层剪力与斜柱中轴向力的关系为
V=2nFncosθ,
(1)
式中:V为子模块承受的剪力;Fn为腹板斜柱的轴力;n为主环梁跨数;θ为斜柱和水平方向的夹角。
再假设构件发生线弹性行为,构件的轴力与对角拉伸应变相关,则腹板斜柱轴力和斜柱应变之间的关系式为
Fn=ASδ=ASEεv,
(2)
式中:AS为斜柱的横截面面积;δ为腹板斜柱的应力;εv为腹板斜柱的应变;E为斜柱材料的弹性模量。
其中斜柱其中斜柱应变εv的表达式如式子模块的剪切变形和腹板斜柱的应力应变关系为
(3)
式中:Δh为剪力作用下子模块的层间水平位移;h为子模块的高度;γ为子模块在剪力作用下的层间水平位移角;e为斜柱的变形量;L为斜柱的长度。
将式(3)代入式(2)中,可以得到斜柱轴力Fn为
Fn=ASEεV=ASEγsinθcosθ,
(4)
子模块斜柱所提供的抗剪能力V为
V=2nASEφVcos2θsinθ,
(5)
可得子模块的剪切刚度KV计算式为
KV=2nASEφVcos2θsinθ。
(6)
2.2 典型六边形子模块弯曲刚度简化计算
以主环梁跨数为n=3的六边形网筒结构模型为例推导子模块弯曲转角的简化计算式,子模块在弯矩M作用下的变形如图3所示。

图3 子模块在弯矩M的作用下的变形图
在弯矩M的作用下,中轴线上与环梁相交节点上的斜柱不产生轴向变形,距离中轴线的距离越远,斜柱产生的轴向变形越大,端部的竖向位移为ΔM。
斜柱轴力Fi的表达式为
Fi=ASδi=ASEεi,
(7)
式中:δi为斜柱应力;εi为弯矩M作用下斜柱的应变;E为斜柱材料的弹性模量。
斜柱的轴向变形和斜柱应变之间的关系为
(8)

将(8)代入(7)中可以得到子模块在弯矩M作用下,斜柱的轴力的表达式为
(9)
子模块承受的弯矩M和斜柱轴力关系式为

(10)
式中:F0为翼缘斜柱的轴力F0=ASEΔMsinθ/L;F1,F2,F3为腹板相交于节点1,2,3的斜柱轴力。
弯曲转角φM和子模块端部产生的竖向位移ΔM与的比值为
(11)
可得子模块承受的弯矩M和弯曲转角之间的表达式为
(12)
由式(12)可得子模块的弯曲刚度KM表达式为
(13)
2.3 典型六边形子模块变形转角计算
由式(4)可得剪切转角φV的计算式为
(14)
由式(13)可得弯曲转角的计算式为
(15)
剪切转角与弯曲转角之间的比值为
(16)
文献[17-18]研究表明,受拉翼缘板向着受压翼缘板立面角部斜柱率先出现塑性铰的现象,塑性铰均呈现出沿着受压翼缘板立面集中向结构上部蔓延的趋势。本文变形转角的计算式则基于结构角部斜柱的轴向变形与子模块的剪切转角与弯曲转角之间的关系建立。
子模块变形转角与腹板角部斜柱的轴向应变之间的关系式为
φVhcosθ+2dφsinθ+Δsinθ=LS。
(17)
六边形网筒结构子模块剪切转角计算式为φV=εV/cosθsinθ,弯曲转角计算式为φM=εM/cosθsinθ,子模块的竖向位移为ΔD=FDh/4nASEsin3θ。
由(15)和(16)可得变形转角φ的计算式为
(18)
3 有限元验证
参考国内外已有工程实例,在控制用钢量相等的原则下通过有限元软件,建立48层六边形网格筒结构模型。参考文献[19]所建立的模型,及《钢管混凝土结构技术规范》GB 50936-2014[20]和《混凝土结构设计规范》GB50010-2010[21]中混凝土抗压强度和弹性模量标准相关参数,确定钢管混凝土构件采用Q345钢,默认刚性连接。所有模型层高均为4 m,建筑总高度192 m,结构尺寸平面为36 m×36 m。斜柱的角度分别为33.69°,53.13°,64.43°和69.44°,环梁部分采用工字型钢800×300×40×20截面。模型中斜柱的具体截面尺寸见表1,基于SAP2000的结构有限元模型如图4所示。

表1 高层六边形网筒结构斜柱截面参数
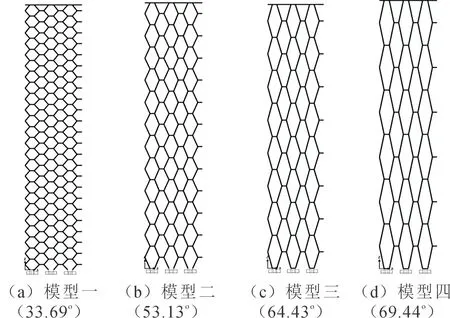
图4 不同斜柱角度的六边形网筒立面
从六边形网筒结构的层间位移角图5可以看出,在顶点集中荷载作用下,当斜柱角度由33.69°增加到64.43°时,结构的层间位移角随着斜柱角度的增加而减小,即抗侧能力逐步增强。当斜柱角度增加至69.44°时,结构的层间位移角随之增大,结构的抗侧能力明显小于其他三种模型。也由此可以得出六边形网筒结构的斜柱角度最优值在33.69°-64.43°之间。因此在设计六边形网筒结构时控制斜柱角度在最优角度范围内,可以达到改善六边形网筒结构抗侧性能的目的。

图5 六边形网筒结构的层间位移角
不同斜柱角度结构底部层间位移角计算结果见表2。通过本文提出的变形转角计算式可以得出模型一到模型四结构底部子模块最大层间位移角分别为1/2336、1/2381、1/2487、1/2070,SAP2000有限元计算结构底部子模块最大层间位移角分别为1/2202、1/2298、1/2489、1/1826,二者的计算误差在6%~13%范围内。
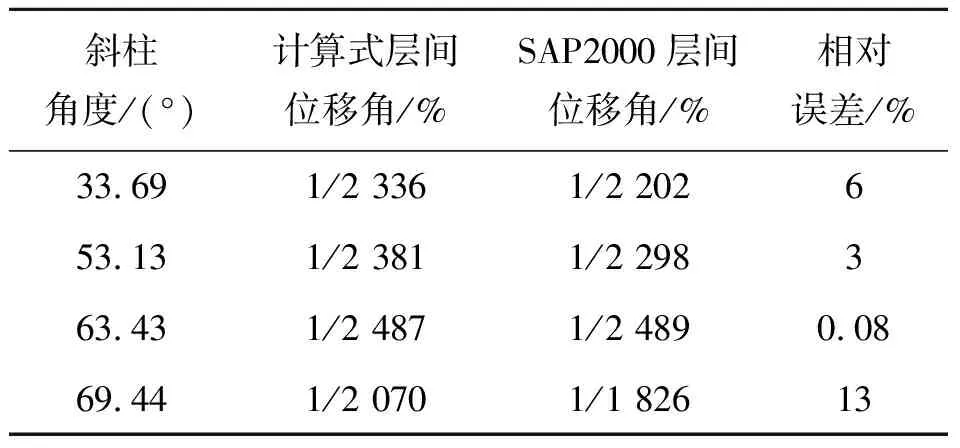
表2 不同斜柱角度层间位移角结果对比
由式(18)可知,子模块所受的剪力和弯矩对变形转角的大小有影响,而结构的侧向荷载分布方式决定结构子模块的剪力和弯矩。对高层建筑结构而言,典型的三种侧向荷载分布形式除了顶点集中荷载外还有侧向均布荷载与倒三角形荷载。当结构底部子模块腹板角部斜柱的轴向应变相同时,六边形网筒结构在三种典型荷载模式下的层间位移角分布图如图6所示,可以得出侧向均布荷载模式下六边形网筒结构的层间位移角最小。
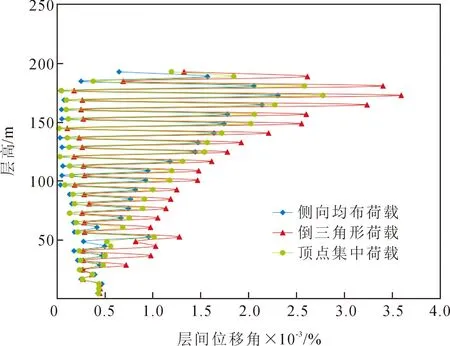
图6 六边形网筒结构三种荷载下的层间位移角
不同荷载模式下结构底部层间位移角计算结果见表3。通过本文提出的变形转角计算式得出,模型一在侧向均布荷载、倒三角形荷载、顶点集中荷载下的最大层间位移角分别为1/2470、1/2189、1/2336。由表3可以得出,SAP2000计算结构底部子模块最大层间位移角分别为1/2356、1/2238、1/2202,二者的计算误差在2%~6%范围内。
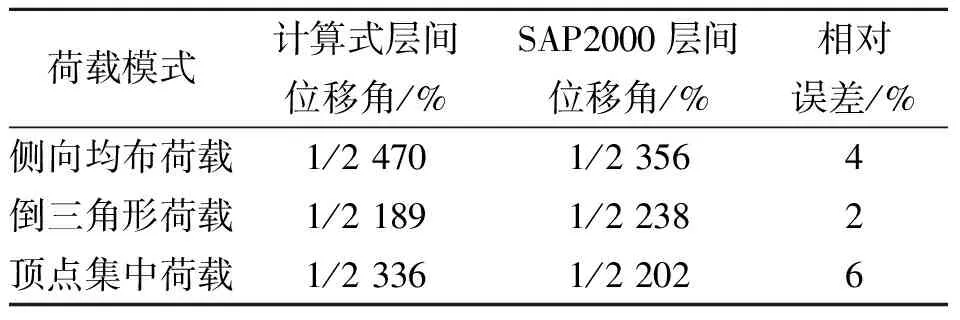
表3 三种荷载模式下层间位移角结果对比
4 结 论
1) 基于六边形网筒结构子模块剪切转角与弯曲转角建立的六边形子模块变形转角计算公式,可以控制该结构的侧向刚度及变形能力。文中推导了六边形网筒结构子模块的侧向刚度、剪切转角和弯曲转角的计算式。通过结构角部斜柱的轴向应变与变形转角之间的关系,建立了子模块变形转角的计算方法,并通过有限元软件进行验证。
2) 在一定范围内六边形网筒结构的层间位移角随着斜柱角度的增大而减小,得出33.69°~64.43°的角度区间为最优角度区间。计算结果表明在不同斜柱角度影响下本文所提结构变形转角简化计算公式结果与有限元模型分析结果误差为0.08%~13%;在侧向均布荷载、倒三角形荷载和顶点集中荷载模式下二者误差为2%~6%。
3) 有限元验证结果表明本文提出的不同斜柱角度和侧向荷载作用下结构子模块变形转角计算方法是比较合理的。高层六边形网筒结构层间位移角受斜柱角度影响较为明显,建议根据结构具体的几何参数,不同斜柱角度的结构应采取不同的层间位移角限值。

