均匀半空间CSAMT折线形线源的场源数值模拟

段跃权,刘云,王紫郡,李雨珊

(云南大学 地球科学学院,云南 昆明 650500)

0 引言

大地电磁测深法(MT)的电磁场频率在音频段(1～104Hz)存在信号弱且易受干扰的缺点,20世纪70年代初,Goldstein等[1]提出人工场源产生音频电磁场以加强天然电磁场,采用MT的测量方式观测音频电磁场。由于所观测电磁场的频率、场强和方向可由人工控制,故称这种方法为可控源音频大地电磁法(CSAMT)。与直流电阻率测深相比,它具有勘探深度大,分辨率高,野外观测系统装置轻便等优点,因此日益受到人们的重视,并且在寻找浅部隐伏金属矿、油气构造勘查、推覆体或火山岩下找煤、地热资源勘查和工程地质勘查等方面,都取得了良好的地质效果[2-11]。

目前,对于CSAMT场源都是基于电偶极子源的假设,并没有考虑有限长电流线源的形态,在地形复杂的地表施工时,非直线型接地电缆源的形态会影响数据处理的结果。针对人工源电磁测深法发射源形态的影响,已有诸多研究成果;其中瞬变电磁法发射源形态的影响研究较为成熟,包括长导线源和回线源形态的影响:陈卫营等[12]阐述了电性源瞬变电磁法发射源形变对观测结果的影响,并且表明发射源的尺寸不能忽略;李展辉等[13]分析了任意形状水平接地导线源对瞬变电磁法计算结果的影响,并表示在垂直于接地导线源方向测量,尤其是进行短偏移距测量时,需考虑到导线源的具体形状,而在轴向方向测量时,在导线形变不大的情况下,可以忽略导线弯曲带来的影响;商天新等[14]考虑了野外实际工作中水平接地导线源形状的任意性,进行了任意形状水平电性源瞬变电磁法全区视电阻率计算;王鹏飞等[15]进行了不规则回线源瞬变电磁法一维正反演研究,通过沿回线积分和时频转换,计算不规则回线内任意一点处的垂直磁场值;李建平等[16-18]进行了任意形状回线源瞬变电磁法研究,提出不管回线源的形状如何,只要将回线的各边看作是多个电偶极子,则回线内任意一点的电磁场均可看成是多个水平电偶极子电磁场的线性叠加,这给本文提供了宝贵的研究思路;然而以上对于发射源形态的影响研究都是基于瞬变电磁测深法展开的。针对CSAMT发射源形态的影响也有很多研究成果,但是都存在一定的局限:刘云鹤等[19]对海洋可控源电磁法发射源姿态的影响做了详细的研究,但研究结果并不能适用于地面可控源电磁法发射源形态的影响;王若等[20]对适合高山峡谷区的CSAMT的观测系统进行了研究,但却只考虑了复杂地形情况下测线的形态,并没有考虑发射源的形态;王艳波[21]对发射源起伏情况下的CSAMT进行了一维正演研究,但着重讨论的是不同收发距下发射源起伏对场值以及视电阻率和阻抗相位的影响;周子琨等[22]讨论了可控源电磁测深法在发射源导线不呈直线的情况下,测点位置视电阻率和电磁场分量的计算方法,利用直角坐标系的平移、旋转,将各个折线段产生的电磁场值转化到同一坐标系中,最后进行积分得到测点位置的总场值,然而该方法的缺陷是当发射源导线的形状较为复杂、折线段数较多时,需要进行多次坐标系的平移、旋转和电磁场分量的计算。此外,张斌等[23]进行了带地形的可控源音频大地电磁法二维正演研究,Xiong等[24]进行了带地形的二维各向异性地层中的线性源CSAMT响应模拟,但是以上学者考虑的都是测区地形起伏对观测结果的影响。目前对于复杂地形CSAMT的研究主要侧重于观测点地形的影响,而对于发射源形态的影响研究并不完善,然而诸多学者研究表明发射源形态的影响不可忽略:陈小斌等[25]在关于人工源极低频电磁波发射源的讨论中提出发射源区大地电流场的流向可能与地表线源的布设路径有关,而不是自动地选择电阻率低的区域流向另一极;刘地渊等[26]实现了任意形状线电流源三维地电场正演,正演结果表明相同模型使用倾斜线源和直线源其地表响应有较大的差别,并且任意形状线电流源更加符合实际应用情况;苏巍等[27]研究发现CSAMT的电场观测数据是由接地两端的传导分量和通电导线感应分量组成,并且感应分量贡献与传导分量贡献相当,因此在数据采集工作中必须考虑导线形状。由此可见发射源形态的影响研究值得重视,并且需要进一步完善,因此有必要进行野外实际CSAMT场源的数值模拟研究。

本文在前人研究成果的基础上,根据电磁场的线性叠加原理推导出任意电流线源激发的电磁场数值计算方法,通过模型计算,分析均匀半空间情况下折线形线源对视电阻率和阻抗相位的影响,为实际工作中的观测结果提供一定的理论指导。

1 均匀半空间线电流源的电磁场

如图1a所示,在均匀半空间地电模型下,当电流线源与测线方向平行时,线源AB在测点P(x,y)处产生的电磁场可以通过电偶极子电磁场积分得到[28]:

(1)

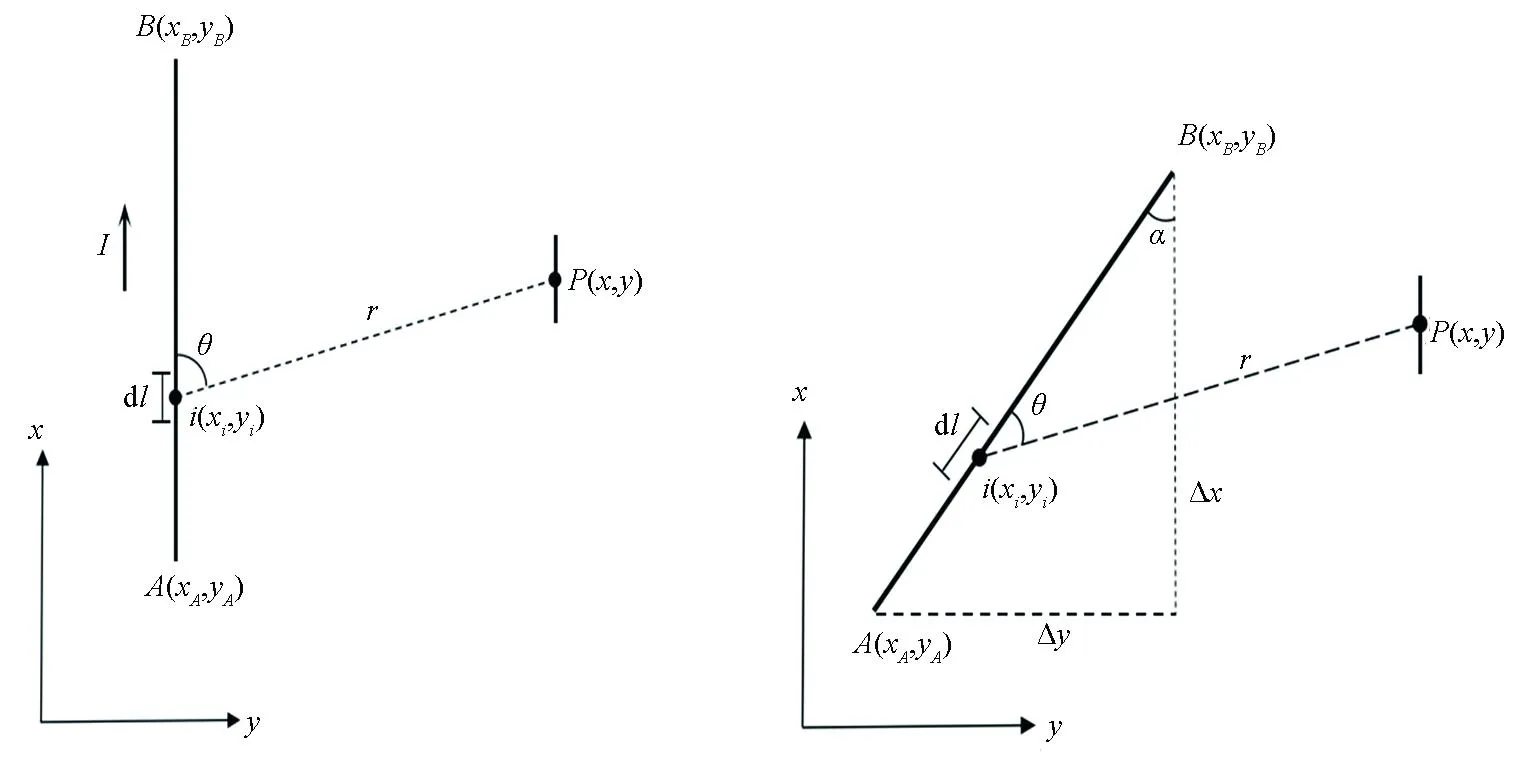
a—线源与测线平行;b—线源与测线呈任意方位角

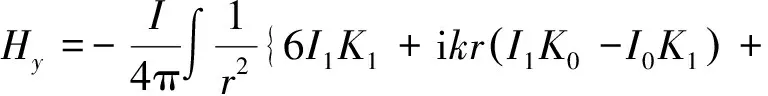
(2)

(3)

当线源与测线呈任意方位角α时,如图1b所示,Δx>Δy,则式(1)和(2)可改写为:

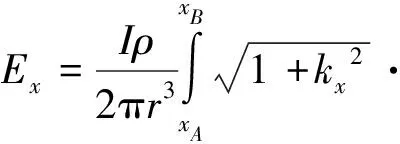
(4)

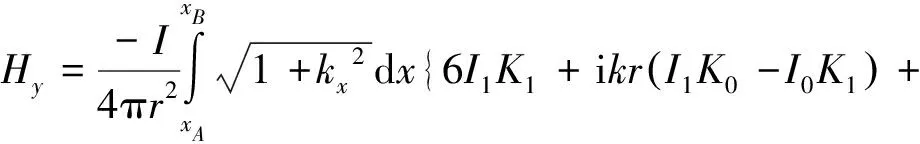
(5)

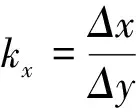
在式(4)和(5)中,需要计算定积分式:

(6)

常规的数值积分法为“5点式”或“10点式”Gauss数值积分法[29]。由于在野外实际中,线源尺寸往往会比较大,“5点式”或“10点式”Gauss数值积分法很难达到较高的计算精度,因此本文采用“n点式”Gauss-Legendre数值求积法[30],其数值滤波计算公式为:

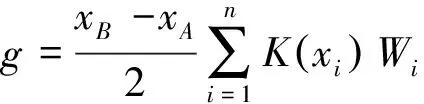
(7)

其中:xB和xA为积分上下限;Wi为第i个滤波系数,xi为Legendre多项式的零点,即线源积分点的横坐标,纵坐标可由式(8)计算得到。n为积分段数,可以根据线源长度任意设定n值大小,选取的n值越大,计算精度较高,则计算耗时较长,具体详见参考文献何光渝等[31]中的数值计算理论和计算程序。

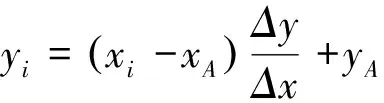
(8)

将线源积分点的坐标(xi,yi)代入到式(3)中,即可求出r和θ。

2 折线形线电流源的电磁场

在实际工作中,由于受到各种条件的限制,很多情况下发射源是任意形状铺设。对如图2所示的任意形状线电流源,可将其近似为M个节点的M-1个折线段构成的折线形线源,每一个折线段可视为如图1b所示的任意方位角线源。此时任意形状电流线源AB在接收点处产生的电磁场可以通过对所有折线段的电磁场线性叠加近似得到[32-33]:

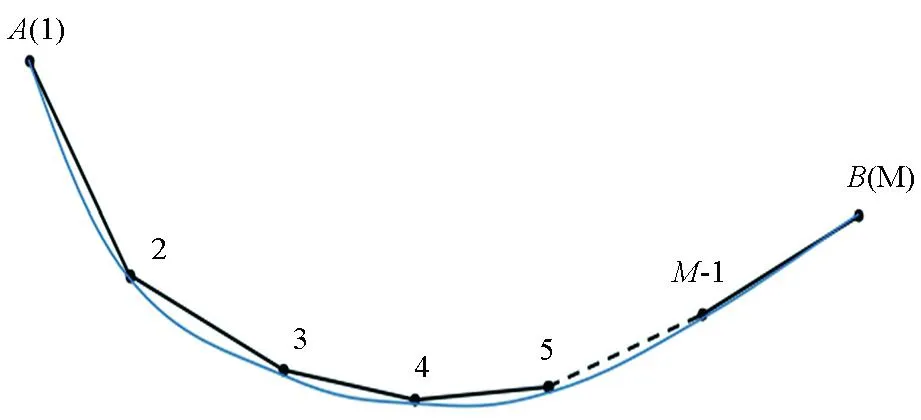
图2 任意形状电流线源剖分示意Fig.2 Schematic diagram of the division of arbitrarily shaped current line source

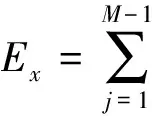
(9)

(10)

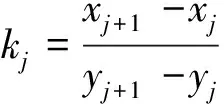
式(9)和(10)分别计算电磁场,利用Cagniard视电阻率计算公式和阻抗相位计算公式即可求得不同频率对应的视电阻率和阻抗相位。用式(11)计算Cagniard视电阻率(下文中简称为视电阻率):

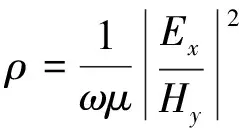
(11)

用式(12)计算阻抗相位:

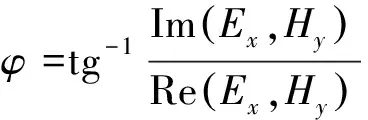
(12)

式中:Re(Ex)和Re(Hy)分别为电场和磁场的实部;Im(Ex)和Im(Hy)分别为电场和磁场的虚部[34]。

3 均匀半空间模型计算

3.1 任意偏角线源的影响分析

在野外进行CSAMT场源布设时,发射源应尽可能平行于测线方向布设,然而实际工作中发射源会与测线方向形成任意方位角。如图3所示,均匀半空间电阻率为100 Ω·m,发射源AB长度为1 500 m,电流强度为10 A,发射源AB与测线方向形成任意方位角α。

图3 发射源与测线呈任意方位角Fig.3 The transmitting source is at an arbitrary azimuth angle to the survey line

定义相对误差的计算公式为:

(13)

其中:f0为方位角α=0°时的计算结果;fα为方位角α>0°时的计算结果。

图4为发射源方位角α从0°～30°时视电阻率和阻抗相位随发射频率的变化特征,收发距为8 000 m。图4a和c分别为视电阻率和阻抗相位随发射频率的变化曲线,图4b为不同方位角α之间的视电阻率相对误差曲线,图4d为不同方位角α之间的阻抗相位绝对误差曲线;其中各误差曲线是以发射源方位角α=0°时的视电阻率和阻抗相位为基准计算得到。从图4中可以看出发射源偏移对视电阻率、阻抗相位曲线的近区和过渡区有较大影响,远区则不受影响,其中近区受到的影响比过渡区大,并且随着发射源方位角α的增大,视电阻率曲线和阻抗相位曲线受到的影响也随之增大;从图4b和d的误差分析中可以看出,当发射源方位角α<15°时,视电阻率相对误差在全频率段小于10%,阻抗相位绝对误差在全频率段小于2°,因此当发射源方位角较小时,由发射源偏移造成的影响可以忽略。

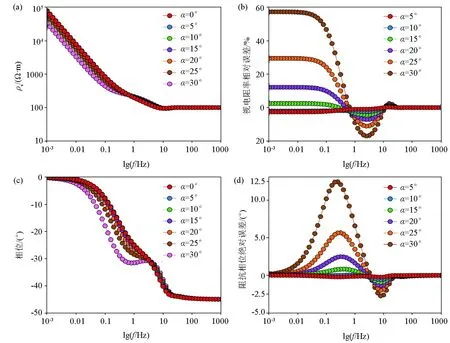
a—不同方位角视电阻率随频率的变化曲线;b—不同方位角视电阻率相对误差曲线;c—不同方位角阻抗相位随频率的变化曲线;d—不同方位角阻抗相位绝对误差曲线

图5为发射源方位角α从0°～30°时视电阻率和阻抗相位随收发距的变化特征,发射频率为1 000 Hz。图5a、c分别为视电阻率和阻抗相位随着收发距的变化曲线,图5b为不同方位角α之间的视电阻率相对误差曲线,图5d为不同方位角α之间的阻抗相位绝对误差曲线;其中各误差曲线同样是以发射源方位角α=0°时的视电阻率和阻抗相位为基准计算得到。从图5看出当r>1 000 m时(r为收发距),发射源偏移对视电阻率和阻抗相位没有影响;当r<1 000 m时,随着收发距减小,测点逐渐靠近场源,视电阻率曲线和阻抗相位曲线出现明显的畸变,此时发射源偏移对视电阻率和阻抗相位的影响较大,即使发射源方位角很小,发射源偏移造成的影响也不可忽略。分析发射源不同方位角对应的视电阻率和阻抗相位随收发距和发射频率的变化特征发现,在远距离进行观测并且发射源方位角较小时,发射源偏移对观测结果的影响可以忽略;然而当发射源方位角较大时,即使是在远距离进行观测,低频段的观测结果依然会受到发射源偏移的影响,因此发射源方位角较大对观测点的影响不能忽略。

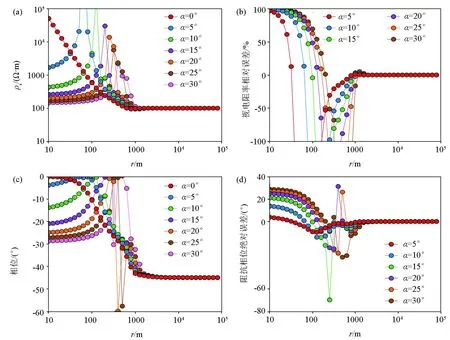
a—不同方位角视电阻率随收发距的变化曲线;b—不同方位角视电阻率相对误差曲线;c—不同方位角阻抗相位随收发距的变化曲线;d—不同方位角阻抗相位绝对误差曲线

3.2 折线形线源的影响分析

折线形线源模型如图6所示,设计了3种发射源模型,保持发射源的长度不变而形态发生弯曲,将其近似为若干个折线段构成的折线形线源,每个折线段与测线方向形成的方位角都为α,其中发射源模型a、b、c的节点数分别为4、5、6。首先计算发射源模型a的折线段方位角α从0°～30°时的视电阻率和阻抗相位;其次分别计算发射源模型a、b、c在折线段方位角相同时的视电阻率和阻抗相位;最后分析折线形线源方位角和节点数(即折线段数)对计算结果的影响。均匀半空间电阻率为100 Ω·m,发射源AB长度为1 500 m,电流强度为10 A,收发距为8 000 m,发射频率为1×10-3～1×103Hz,共61个频率点。

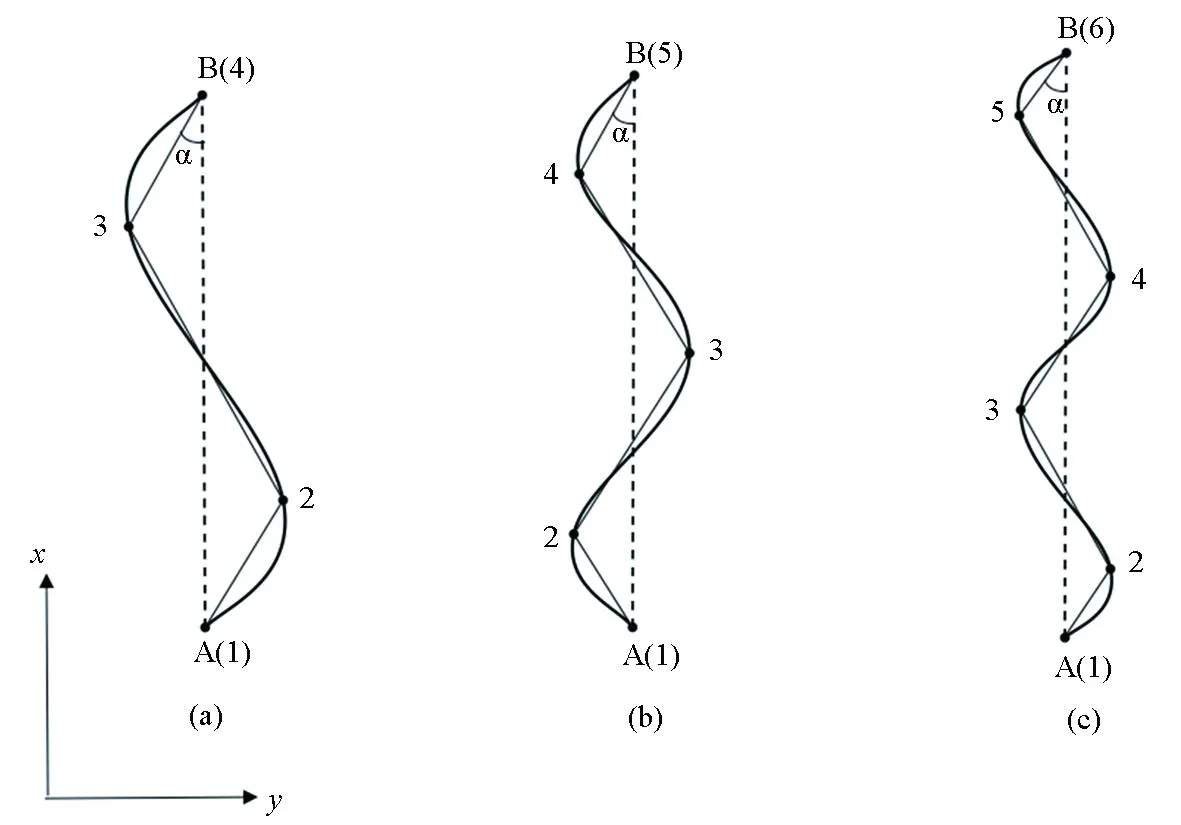
a—发射源模型a,节点数为4;b—发射源模型b,节点数为5;c—发射源模型c,节点数为6

发射源模型a不同折线段方位角对应的视电阻率和阻抗相位计算结果如图7、图8所示。图7a、c为视电阻率和阻抗相位随发射频率的变化曲线,b和d分别为不同方位角之间的视电阻率和阻抗相位误差曲线,收发距为8 000 m;当f>10 Hz(远区,f为发射频率),不同方位角对应的视电阻率曲线和阻抗相位曲线相互重合,且误差值为零,当f<10 Hz时,随着方位角增大,视电阻率曲线的过渡区范围由1 Hz1 000 m时(r为收发距),不同方位角折线形线源对视电阻率和阻抗相位都没有影响,当r<1 000 m时,曲线的变化情况和图7一致。这表明折线形线源只影响视电阻率曲线和阻抗相位曲线的过渡区和近区,对远区则没有影响,这种影响体现为随着折线段方位角增大,视电阻率曲线过渡区和近区的位置向低频处偏移,而阻抗相位曲线在过渡区和近区会出现明显的畸变。

a—折线形线源不同方位角视电阻率随频率的变化曲线;b—折线形线源不同方位角视电阻率相对误差曲线;c—折线形线源不同方位角阻抗相位随频率的变化曲线;d—折线形线源不同方位角阻抗相位绝对误差曲线

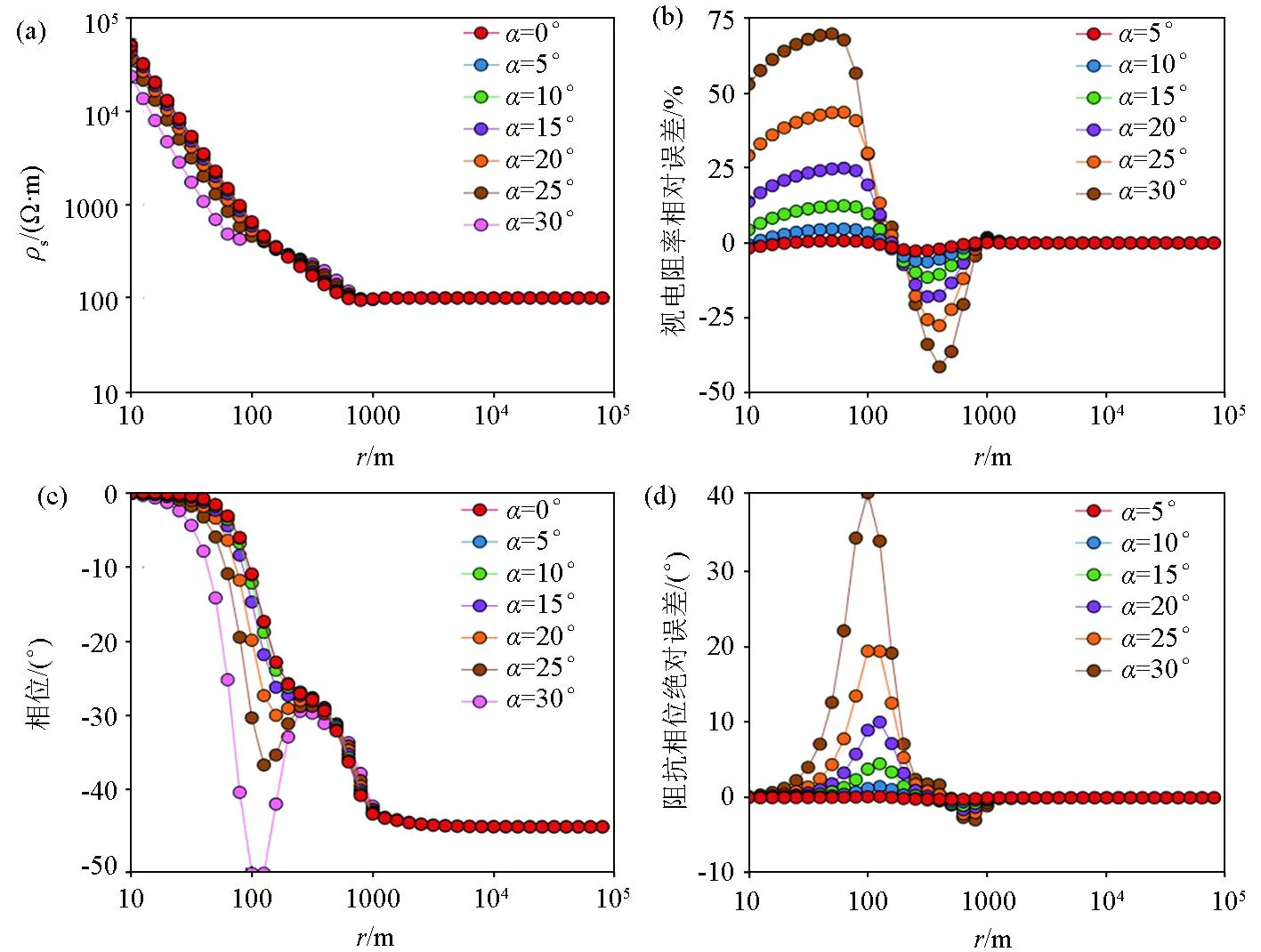
a—折线形线源不同方位角视电阻率随收发距的变化曲线;b—折线形线源不同方位角视电阻率相对误差曲线;c—折线形线源不同方位角阻抗相位随收发距的变化曲线;d—折线形线源不同方位角阻抗相位绝对误差曲线

发射源模型a、b、c在折线段方位角相同时视电阻率和阻抗相位的计算结果如图9所示,从图9中可以看出,在折线段方位角都相同的情况下,3种发射源模型计算得到的视电阻率曲线和阻抗相位曲线一致,远区视电阻率和阻抗相位的误差均为零,近区视电阻率最大误差不超过2%,阻抗相位最大误差不超过0.3°。因此折线形线源对视电阻率和阻抗相位曲线近区和过渡区的影响主要是由各个折线段方位角引起的,与折线形线源的节点数(即折线段数)无关,折线段方位角越小,对测点的视电阻率、阻抗相位的影响越小;当某一个折线段方位角很小时,可以忽略该折线段方位角带来的影响并将其近似为折线段方位角为0°的情况,如图10所示忽略了发射源模型d中折线段方位角α1和α4的影响,只考虑折线段方位角α2和α3的影响,从而将发射源模型d简化为模型e处理,分别计算发射源模型d和模型e对应的视电阻率和阻抗相位,计算结果如图11所示。

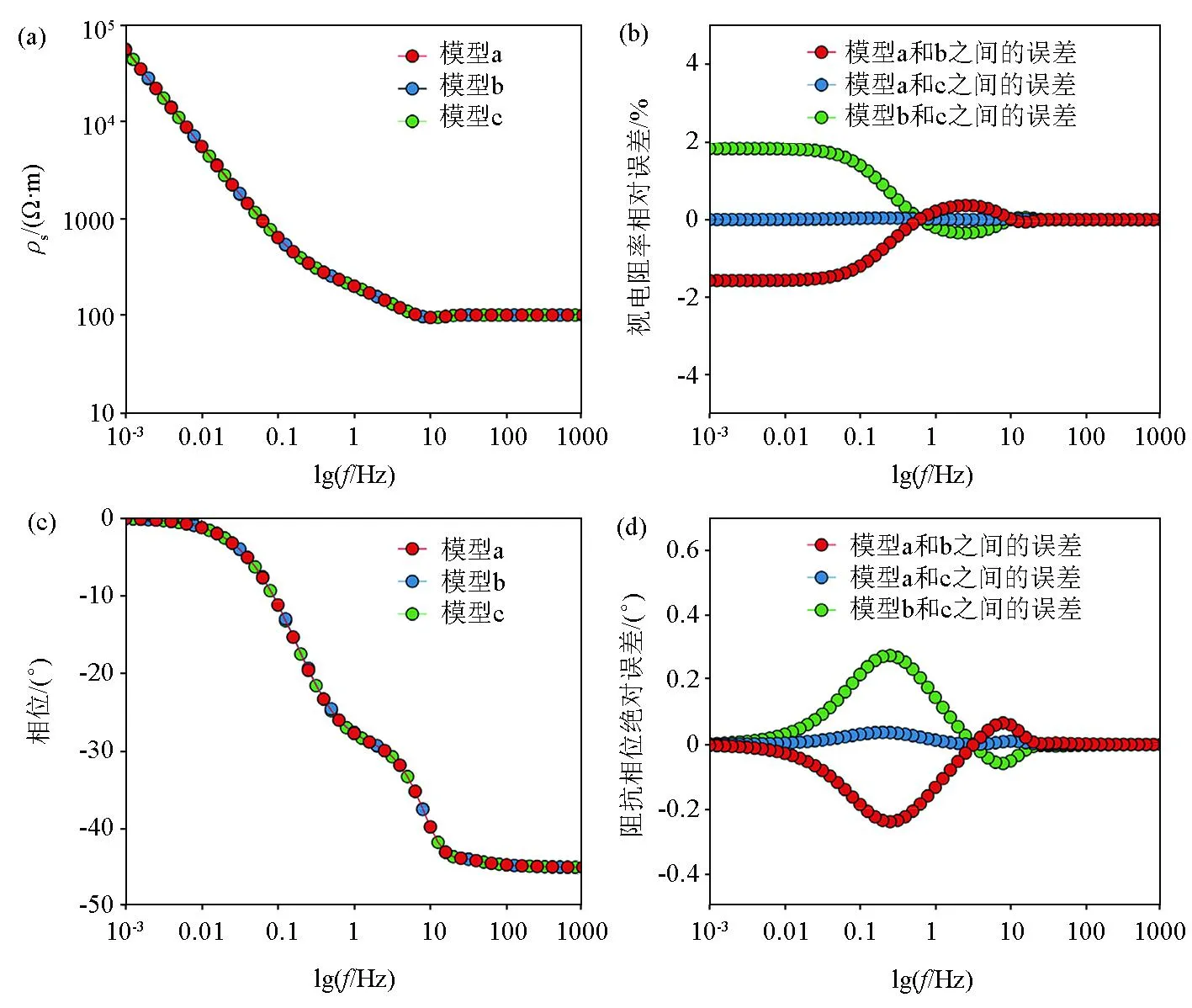
a—发射源模型a、b、c的视电阻率曲线;b—发射源模型a、b、c之间视电阻率的相对误差曲线;c—发射源模型a、b、c的阻抗相位曲线;d—发射源模型a、b、c之间阻抗相位的绝对误差曲线

d—任意形状折线形发射源模型;e—简化后的折线形发射源模型

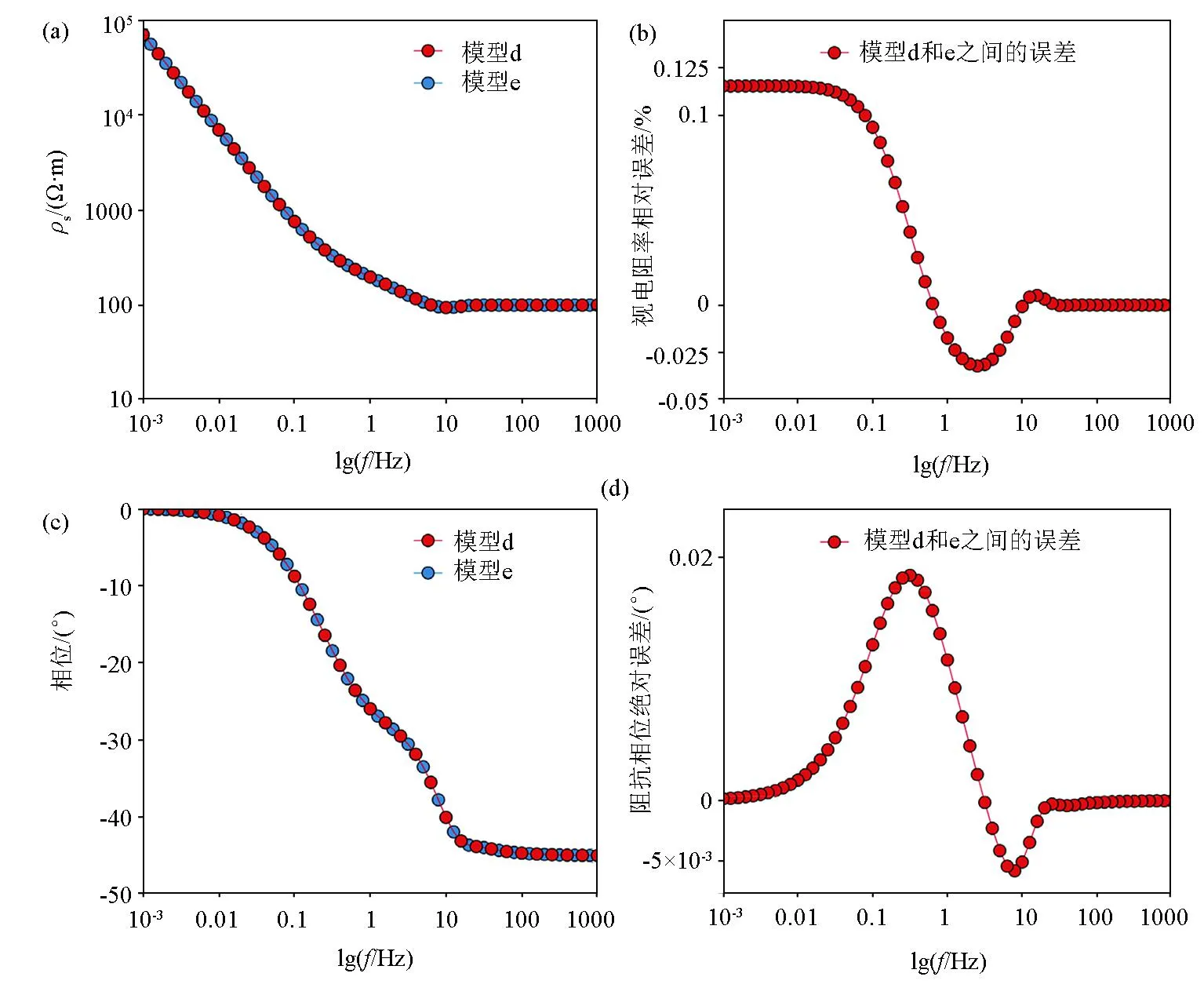
a—发射源模型简化前后的视电阻率曲线;b—发射源模型简化前后视电阻率相对误差曲线;c—发射源模型简化前后的阻抗相位曲线;d—发射源模型简化前后阻抗相位绝对误差曲线

从图11中可以看出发射源模型d和模型e计算得到的视电阻率曲线和阻抗相位曲线相互重合,误差分析显示两种发射源模型计算得到的视电阻率误差不超过0.125%,阻抗相位误差不超过0.02°;因此把发射源模型d近似为模型e是合理的;在野外工作中,需要考虑折线形线源对观测结果的影响,当某一个折线段方位角很小时,可以将其忽略并近似为直线源进行处理,这样既可以充分考虑发射源的形态又可以提高工作效率。

4 结论

本文根据电磁场的线性叠加原理推导出折线形电流线源激发的电磁场数值计算方法;对于任意形状的电流线源,先将其近似为若干个折线段构成的折线形线源,再将每一个折线段剖分为多个电偶极子,最终将电偶极子的电磁场线性叠加。通过对不同的折线形线源模型计算,分析均匀半空间情况下折线形线源对视电阻率和阻抗相位曲线的影响,得到如下结论:①折线形线源只影响Cagniard视电阻率曲线和阻抗相位曲线的过渡区和近区,对远区没有影响,这种影响体现为随着折线段方位角增大,Cagniard视电阻率曲线过渡区和近区的位置向低频处偏移,而阻抗相位曲线在过渡区和近区会出现明显的畸变。②收发距越大,且折线段方位角越小时,观测结果受到的影响越小,因此应该选择合适的收发距,并尽量保持发射源与测线方向平行。③折线形线源对Cagniard视电阻率和阻抗相位曲线的影响主要是由各个折线段方位角引起的,与折线形线源的节点数(即折线段数)无关,当折线段方位角很小时,可以将其忽略并近似为直线进行处理,这样既可以充分考虑发射源的形态又可以提高工作效率。