考虑软矿物纵横比的页岩岩石物理建模及其应用

杨骐羽, 李景叶, 吴凡, 李文瑾, 崔津铭

(1.油气资源与探测国家重点实验室,北京 102249; 2.中国石油大学(北京) 地球物理学院,北京 102249)

0 引言

建立更精确的页岩岩石物理模型,将有助于分析储层物性参数与弹性参数的关系,寻找敏感性参数,开展“甜点”预测等工作。1981年,Jones和Wang[1]提出页岩内部垂直定向排列的裂缝所引起的HTI(horizontal transverse isotropy)各向异性程度远小于由颗粒定向排列导致的VTI(vetical transverse isotropy)各向异性。对于垂向裂缝不发育的页岩储层,通常建立横向各向同性页岩岩石物理模型。

1994年,Hornby等[2]将自相容模型(self compatible model,SCA)和微分等效介质模型(differential equivalent medium model,DEM)推广至各向异性,为各向异性储层岩石物理建模提供理论基础。2007年,原宏壮[3]对Xu-White模型进行改进,将孔隙分为黏土孔隙与砂岩孔隙,建立了各向同性双重孔隙泥质砂岩有效介质模型。Bandyopadhyay[4]、Wu等[5]与胡起等[6-7]分别考虑到页岩储层中有机质的各向异性与孔隙形状对弹性模量的影响,建立页岩岩石物理模型,但均忽略了黏土的各向异性及其形状的变化。2015年,王璞等[8]认为孔隙形状与矿物形状共同影响着岩石的纵横波速度,建立适用于各向同性介质的S-S模型。2019年,张琦斌等[9]基于各向同性假设,将孔隙分为干酪根中存在的有机孔与混合物中的粒间孔,建立了一种考虑含混合流体干酪根的页岩岩石物理模型,该模型的前提假设限制了模型精度。Ruiz等[10-11]通过实验室测量,证明了岩石基质中存在软孔隙(低孔隙纵横比),分别讨论了软孔隙与单一孔隙纵横比对岩石物理建模的影响,研究说明考虑页岩储层中的孔隙变化是有必要的。此后,桂俊川等[12]、张益明等[13]、刘致水等[14]以不同方法精细描述孔隙形状,建立了不同的岩石物理模型。

考虑到页岩储层的各向异性的特征,“甜点”区的孔隙度一般在0.01附近,且矿物形状与孔隙形状共同影响着储层的弹性模量[3]。本文基于页岩储层的实际地质情况,建立了同时考虑孔隙类型、孔隙形状与软矿物形状的横向各向同性的页岩岩石物理模型,基于粒子群法反演输入参数,开展纵横波速度、各向异性参数与岩石力学参数计算的工作,并结合实际资料进行验证。

1 页岩岩石物理建模及参数反演

1.1 储层特征分析

我们针对鄂尔多斯盆地某页岩储层建立岩石物理模型。梁晓伟等[15]对鄂尔多斯盆地页岩储层展开系统研究,其研究区内岩石中存在的主要陆源碎屑矿物成分为石英、长石和黏土矿物,其中石英含量在16.9%～80.4% 之间,斜长石与钾长石的总量一般为 9%～43%,黏土矿物含量在 8%～62% 之间,孔隙度主要介于0.85%～9.57%之间。曹尚等[16]对鄂尔多斯盆地孔隙发育特征展开对比分析,认为页岩储层主要发育着粒间孔、粒内孔和有机孔三类孔隙,其中粒间孔主要发育在黏土矿物与石英、长石等刚性颗粒间,粒内孔主要发育在脆性矿物内,有机孔多发于有机质与黏土矿物的分界面上。

图1为研究工区储层测井曲线,其中,CAL为井径曲线、DEN为密度曲线、CNL为中子孔隙度曲线、GR为自然伽马曲线、RT为电阻率曲线;TOC为干酪根含量曲线;VSH为泥质含量曲线、POR为孔隙度曲线、SW为含水饱和度曲线;图中箭头所指区域为测井曲线指示的“甜点”区。本文选取黑色线框(2 250～2 290 m)区域为研究区进行岩石物理建模。在深度为2 269 m和2 290 m处有明显的扩径现象,可能导致预测精度的降低。目标层内干酪根含量基本高于0.02,具有工业开发价值;孔隙度整体较小,大致在1%附近,含水饱和度较高,大致在99%附近,且变化趋势不大。页岩在微观尺度下黏土、干酪根以及不为球形孔隙的定向排列,使得页岩具有较强的各向异性特征,且页岩储层内部矿物成分和孔隙类型较为复杂。

图1 测井曲线Fig.1 Well logging curve

1.2 岩石物理建模框架及其原理

研究区具有孔隙度低、干酪根含量高、泥质含量高的特征,扁平状孔隙、黏土与干酪根的定向排列均使得页岩具有较强的各向异性特征。若考虑过多因素进行岩石物理建模,必将使得模型的输入参数增加,给正演模拟带来一定困难。

页岩储层矿物成分复杂,本文将固体矿物分为脆性矿物(石英与长石)与软矿物(黏土、干酪根)两类。认为脆性矿物表现为各向同性特征,基于VRH平均模量(式1)计算脆性矿物混合物的弹性模量:

(1)

式中:MVRH为Voigt上限与Reuss下限的算术平均;MV与MR分别为Voigt基于等应变平均提出的Voigt上限模量[17]和Reuss基于等应力平均提出的Reuss下限模量[18],具体形式如下:

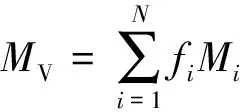
(2)

(3)

式中:fi为各组分的体积含量,Mi为各组分弹性模量。VRH模型将不同组分的矿物均匀混合,通常被用于估算混合物的弹性模量。

考虑黏土与干酪根相互嵌合的实际情况,计算各向异性两相介质混合的弹性模量。对于多相介质混合物, Berryman[19]给出了各向同性多相介质的SCA模型。两相介质混合时,不少学者均发现SCA模型的第二相介质含量需要为40%～60%时,才能保证介质双相流通[3]。因此,SCA模型通常与DEM模型共同使用,建立双相介质;即,先以第二相介质含量为50%利用SCA模型混合,再利用DEM模型调节包含物的含量。参考桂俊川等[12]计算多相介质等效模量的方法,结合各向异性SCA与DEM模型建立黏土与干酪根混合物(介质I),如式(4)和(5)。

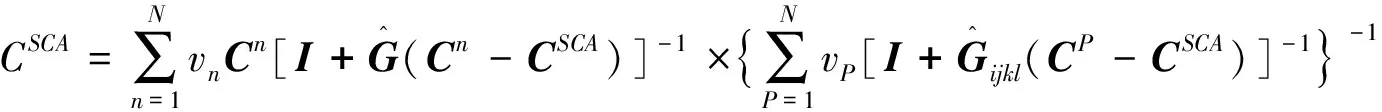
(4)

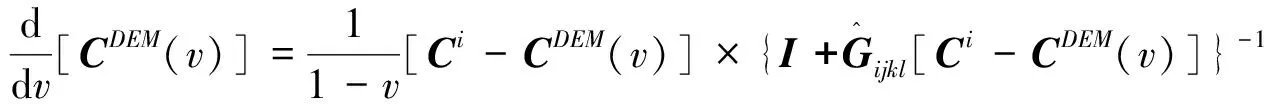
(5)

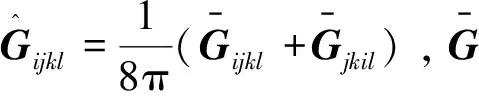
建立矿物混合物后,将储层孔隙按其类型分为脆性矿物中存在的粒内孔、介质I中存在的有机孔以及所有矿物混合物中的粒间孔,并利用各向异性DEM模型添加不同种类的孔隙。最后,基于Brown和Korringa[20]提出的各向异性流体替换模型(式6),得到饱和流体页岩岩石物理模型:

(6)

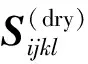
图2 岩石物理建模流程Fig.2 Flow chart of petrophysical modeling

1)选取长石的体积模量为37.5 GPa,剪切模量为15 GPa;石英的体积模量为37 GPa,剪切模量为4 GPa。工区内缺少脆性矿物含量,考虑到石英与长石模型差异不大,基于工区地质背景认为工区内4脆性矿物占比为常数(石英在混合矿物中占比为75%)。利用VRH模型计算得到混合矿物的等效模量,并基于各向同性DEM模型在混合矿物中添加粒内孔将其作为背景介质。

2)选取黏土的体积模量为21 GPa,剪切模量为7 GPa;干酪根的体积模量为2.9 GPa,剪切模量为2.7 GPa。干酪根的弹性模量较小,且实际储层中黏土与干酪根是相互嵌合的。考虑软矿物的各向异性特征,基于各向异性SCA+DEM模型建立介质I,并基于各向异性DEM模型中加入有机孔建立介质II。

3)基于各向异性DEM模型,先后将介质II与粒间孔逐步加入到步骤1)所建立的背景介质中,建立干页岩。

4)考虑工区内含水饱和度较高,基于地质背景认为孔隙内的混合流体为水和天然气。基于Reuss等应力平均模型计算混合流体的弹性模量。最后,利用各向异性流体替换模型(BK)进行流体替换,建立饱和流体页岩岩石物理模型。

1.3 模型参数的确定及其反演

岩石物理模型的输入参数可以分为各组分含量、各组分模量及描述孔隙与矿物几何形状的三类参数,其中各组分含量(干酪根含量、黏土含量、孔隙度等)可由工区测井曲线获得,各组分模量可通过查阅获得(如表1)。因此,本文所建立的岩石物理模型仅剩下3个参数:软矿物纵横比、孔隙纵横比和不同种类孔隙占比,其中,软矿物纵横比与孔隙纵横比均为地层压力、地应力等共同作用的结果,不易通过选取某一常数等效模拟。

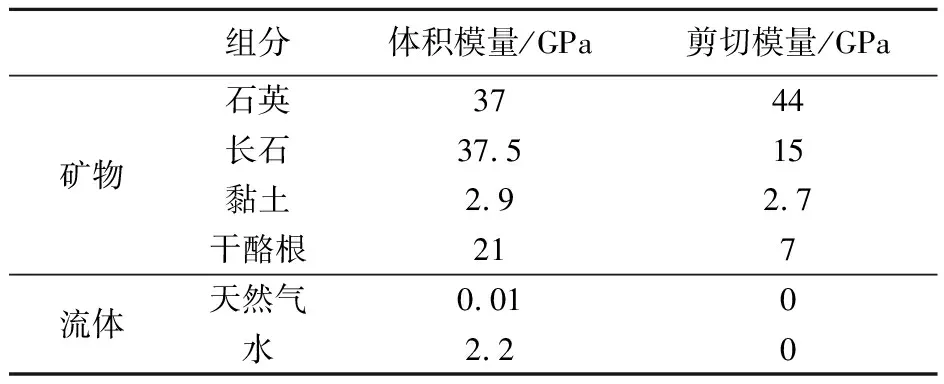
表1 各组分弹性模量[21-22]Table 1 Elastic modulus of each component[21-22]

本文将孔隙细分为粒内孔、粒间孔和有机孔三类。将泥质含量设定为0.4,干酪根含量设定位0.05,含水饱和度设定为0.9,密度设定为2.2 g/cm3,分析仅加入粒间孔与加入三类孔隙对速度的影响,如图3所示。图3中黑线和红线分别为仅加入粒间孔得到的纵波速度曲线与横波速度曲线;带星号的黑线和红线分别为本文所提出的将孔隙细分为粒内孔、有机孔与粒间孔得到的纵波速度与横波速度,且三类孔隙占比为1∶1∶1。将孔隙细分后的速度明显降低;因此,有必要将孔隙按照储层实际情况进行细分。三类孔隙占比对速度的影响如图4所示,其中黑线表示粒内孔、有机孔、粒间孔的占比为1∶1∶1,蓝色星线表示占比为3∶1∶1,红色点线表示占比为1∶3∶1,绿色圈线表示占比为1∶1∶3。当孔隙度小于0.05时,纵波速度与横波速度并未受到孔隙占比的变化,其值基本没有变化;当孔隙度大于0.05时,纵波速度与横波速度随着孔隙占比的变化略微波动,但并不明显。基于上述分析,本文参考Xu-White模型,将各类孔隙按矿物在总矿物中的占比进行分配。

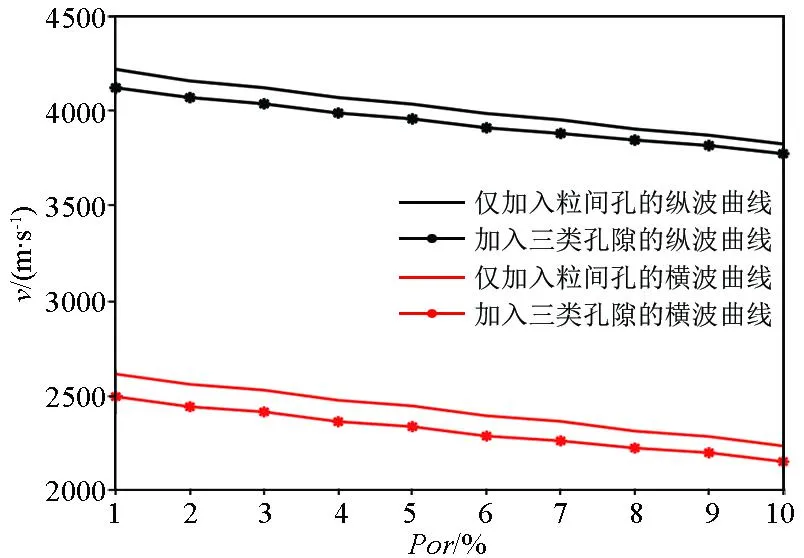
图3 单一孔与三类孔对速度的影响Fig.3 Effect of single hole and three kinds of hole on velocity

图4 不同孔隙占比对速度的影响Fig.4 Influence of different pore ratio on velocity

设定与上文相同参数,分析与形状相关的参数对速度和各向异性参数的影响。三类孔隙的孔隙纵横比均由硬孔隙(孔隙纵横比为1)与软孔隙(孔隙纵横比为0.01)加权得到:

α=Vsoft×0.01+(1-Vsoft)×1,

(7)

式中:α为孔隙纵横比;Vsoft为软孔隙占比。

软孔隙占比越大孔隙越扁平,各向异性越明显。设定软矿物纵横比为0.5,分析软孔隙占比对纵横波速度与Thomsen各向异性参数ε、δ、γ的影响,如图5与图6所示。软孔隙占比小于0.9时,纵横波速度与各向异性参数均对其不敏感;软孔隙占比大于0.9时,纵横波速度与各向异性参数明显降低,即孔隙越扁平,速度变化就越剧烈且各向异性程度越高。

图5 软孔隙占比对速度的影响Fig.5 Influence of soft pore ratio on velocity

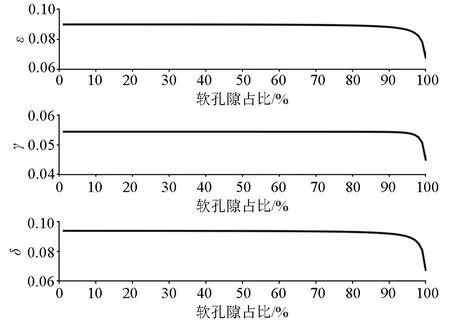
图6 软孔隙占比对Thomsen各向异性参数的影响Fig.6 Influence of soft pore ratio on Thomsen anisotropy parameters

设定软孔隙纵横比为0.5,分析软矿物纵横比对纵横波速度与各向异性参数的影响,如图7与图8所示。软矿物纵横比与速度呈正相关,随着软矿物的增加,横波速度的变化逐渐缓慢;相比于软孔隙占比,速度对软矿物纵横比更敏感。软矿物纵横比与各向异性参数ε、δ呈负相关,与各向异性参数γ呈正相关,随着软矿物的增加各向异性参数的变化逐渐缓慢;相比于软孔隙占比,各向异性参数也对软矿物纵横比更敏感。

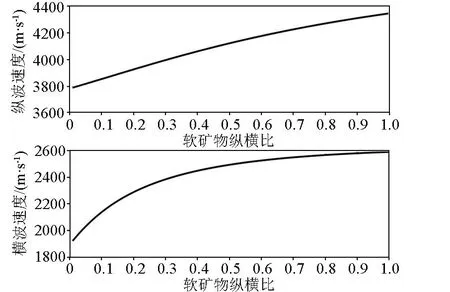
图7 软矿物纵横比对速度的影响Fig.7 Influence of soft mineral aspect ratio on velocity

图8 软矿物纵横比对Thomsen各向异性参数的影响Fig.8 Influence of soft mineral aspect ratio on Thomsen anisotropy parameters

软孔隙占比与软矿物纵横比均对弹性参数较为敏感,在岩石物理建模中不易选取某一常数模拟。本文利用粒子群法反演软矿物纵横比与软孔隙含量,具体流程如图9所示。图9中,a、Vsoft分别为软矿物纵横比与软孔隙占比。首先生成模型输入参数的初始种群,构造的个体最佳适应度与群体最佳适应度更新种群粒子位置,进行粒子群迭代直至满足终止条件,最终输出最佳模型参数软矿物纵横比与软孔隙占比。

图9 岩石物理参数反演流程Fig.9 Inversion flow of petrophysical parameters

2 模型测试与应用

选取工区长7的井资料用于验证岩石物理模型的准确性与适用性。基于粒子群法的模型参数反演结果如图10a、b所示。参考Thomsen 给出的横向各向同性介质弹性参数的表达式(式 8)[23]计算纵横比速度,其结果如图10c～e所示,其中黑色实线与红色点线分别为模型得到的速度曲线和测井得到的速度曲线,图10e中黑色实线与黑色点线分别为模型得到的纵波速度与实际纵波速度的比值和模型得到的横波速度与实际横波速度的比值。由于纵波速度参与构造最佳适应度,模型得到的纵波速度与测井得到的纵波速度基本吻合,其相对误差介于[-0.03,0.03]之间,模型得到的横波速度与测井得到的横波速度吻合度低于纵波速度,但仍具有一定的精度,其相对误差介于[-0.09,0.09]之间。基于Thomsen给出的各向异性参数与等效刚度系数的关系式[20],其结果如图11a～c所示;在测井指示的“甜点”各向异性参数ε、δ明显增加,γ明显降低。基于桂俊川等[24]给出的VTI介质垂直方向与水平方向杨氏模量和泊松比与等效刚度系数的关系式,计算各向异性杨氏模量、泊松比,其结果如图11d、e所示,其中蓝色实线与绿色实线分别为垂直方向与水平方向的岩石力学参数。参考Guo等[25]建立的脆性指数,计算常规基于各向同性假设计算的脆性指数与模型输出的各向异性脆性指数,图11f中黑色实线为各向同性理论计算得到的脆性指数。基于本模型计算得到的各向异性脆性指数与各向同性计算得到的结果具有相同变化趋势,各向异性脆性指数分别从水平方向与垂直方向刻画脆性变化,考虑到储层的各向异性特征使得其具有更多细节变化。

图10 反演曲线与模型得到的速度曲线Fig.10 Inversion curve and velocity curve obtained by the model

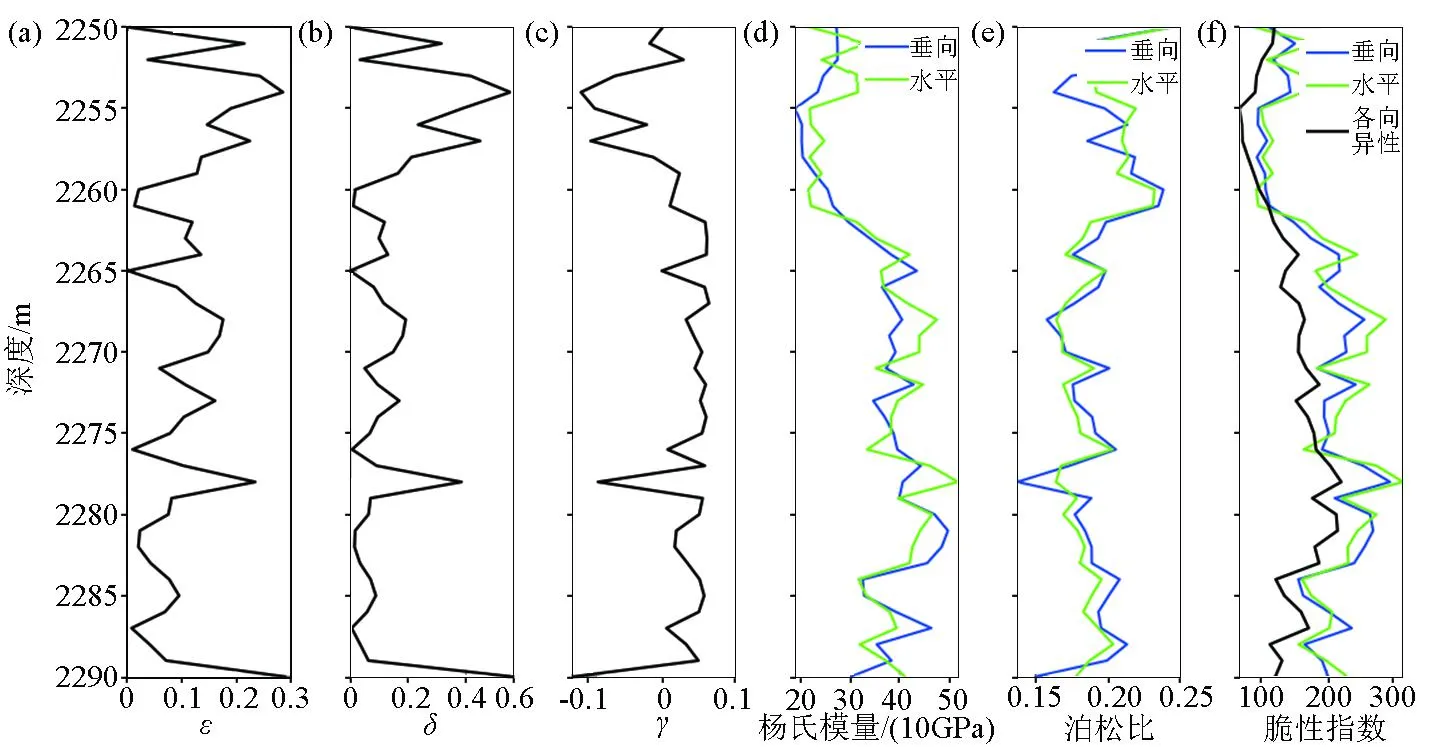
图11 各向异性参数与岩石力学参数计算结果Fig.11 Anisotropy parameter and rock mechanics parameter calculation results

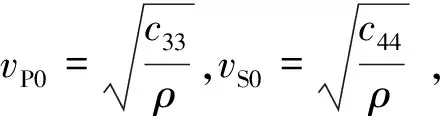
(8)

式中:c*为岩石物理模型输出的等效刚度系数;vP0、vS0为沿对称轴方向传播的纵波速度与横波速度;ε、γ、δ为各向异性参数,ε描述了纵波速度在垂直与水平方向的差异,γ描述了水平方向SH波与SV波速度的差异。

3 结论

本文同时考虑页岩储层孔隙类型、孔隙形状与软矿物形状,利用粒子群法反演主要参数,建立了一种更精确描述页岩储层的横向各向同性岩石物理模型,开展了基于该模型的横波速度预测、各向异性参数与岩石力学参数计算的工作。结合研究区实际测井资料和常规各向同性岩石力学参数计算结果对比验证,模型输出的波速度具有较高精度,各向异性参数与岩石力学参数具有一定的参考价值,本文所提出的模型对页岩储层具有一定的应用性。