基于自适应小波去噪的局部放电超高频信号测量方式

储后广，许广虎，何丹东，韩雪峰

（1.国网新疆电力有限公司电力科学研究院，乌鲁木齐 830000；2.湖南工业大学 电气与信息工程学院，株洲 412007）

局部放电是高压电器设备运行过程中的一种常见现象，其主要是在电场作用下，电力设备导体和接地体之间的绝缘结构受损或者被击穿[1]，导致绝缘劣化压电器设备一旦发生局部放电，会发生不均匀电晕，直接影响脉冲电流[2]，对于电力系统的安全运行存在较大影响[3]。而局部放电超高频信号检测是判断高压电器设备是否存在绝缘缺陷的重要依据[4]，因此，如何可靠完成局部放电过程中高频信号的检测，是保证电网安全运行的基础。

文献[5]为实现局部放电信号的可靠检测，依据光纤传感系统进行信号检测，该方法在应用过程中，具有较好的灵敏度，但是由于超高频信号通常情况下位于气体绝缘组合电器室内，因此其检测结果的精准性会受到影响。文献[6]以采集的信号信息为依据，通过混沌阵子对其进行处理，利用相态判断完成局部放电信号检测，但是该方法在应用过程中采集的信号会存在大量噪声，影响最终的检测结果。

本文为实现局部放电超高频信号测量，提出基于自适应小波去噪的局部放电超高频信号测量方法。

1 局部放电超高频信号测量

1.1 局部放电超高频信号检测方法

本文为实现局部放电过程中超高频信号检测，提出基于自适应小波去噪的局部放电超高频信号检测方法，该方法整体包含3 个模块，分别是信号采集模块、信号处理模块以及信号检测模块，方法整体架构如图1 所示。

图1 局部放电超高频信号检测方法框架Fig.1 Method framework of local discharge UHF signal detection

（1）信号采集模块：该模块主要由局部放电传感器、信号调节单元、开关电路、电源、时间交错模数转换（TLADC）技术等部分组成，其主要作用是采集局部放电信号，为局部放电过程中产生的超高频信号检测提供可靠依据。

（2）信号处理模块：该模块的主要作用是完成采集的局部放电信号的存储和降噪等，主要包含数据库、自适应小波降噪、信号增强等功能。

（3）信号检测模块：该模块作为整个方法的核心模块，同时也是实现超高频检测的模块，其主要以小波降噪处理后的信号为依据，利用Duffing 振子和混沌理论，实现局部放电过程中的超高频信号检测。

1.2 基于TLADC 技术的局部放电信号采集

信号采集模块在理想状态下，采样频率用fs表示，在该频率下，ADC 的信号采集结果与TLADC 集成信号结果一致。在实际应用过程中，每一个ADC的应用性能均会存在一定差异，会导致每个传感器采集通道之间发生失配误差。当不存在误差时，单通道的ADC 信号采集的理想输出结果计算公式为

式中：Ts为采样周期；k 为第k 个传感器通道；yk为采集的数字信号序列；M 为ADC 芯片数量；n 为ADC的分辨率。

在实际应用过程中，考虑失配误差完成ADC 输出的信号采集结果，其计算公式为

式中：gk、tk、ok均为失配误差，三者分别对应通道增益、偏置失配、时延失配。

由于上述误差会影响数据最终的采集效果，因此，分别对3 种误差进行校正，以此保证局部放电信号的采集效果。

1.3 基于自适应小波的局部放电信号降噪处理

采集的局部放电信号传送至信号处理模块中，该模块以小波降噪算法为基础，采用鲸鱼优化算法对其阈值选择以及进行自适应优化后，形成自适应小波降噪方法，用于完成采集的局部放电信号的降噪处理[7]。

基于自适应小波的信号降噪的详细步骤如下所述：

（1）获取小波库中的小波γi，对输入的yk［n］进行第一层小波分解，获取近似系数和细节系数，分别用a1，k和d1，k表示。

（2）计算第一层小波分解后的最优小波选择指标β，获取计算结果中的最大值，将其定义为当前最优小波，并记录该小波结果、近似系数以及细节系数。

（3）由于细节系数dj，k中包含大量白噪声，在对其进行分解过程中，细节系数会逐渐和局部放电噪声信号混合，因此，会导致细节系数dj，k逐渐呈现非噪声特性，对细节系数进行白化检验，并按照式（3）的检验条件进行判断，其公式为

式中：N 为小波系数长度；ρ（i）为信号相关序列。

依据式（3）进行判断后，如果满足该条件，则说明xj是白噪声，记录xj当前的近似系数，并将其作为目标分解信号[8]，并回转至步骤2，如果不满足则进行下一步。

（4）对分解获取细节系数dj，k进行分层处理后，采用鲸鱼优化算法进行最优阈值ψ 的选择，并保留该结果。

（5）将获取的每层最优阈值带入下述公式中，进行所有dj，k的小波降噪，其公式为

式中：si为测量信号；ξ 为决定阈值函数形状的参数；φ（si，ψ）为阈值函数。

（6）利用各层最优小波，对获取的最后一层近似系数和降噪后的dj，k进行小波重构处理，以此获取降噪后的局部放电信号。

1.4 基于Duffing 振子和混沌理论的超高频信号检测方法

依据上述小节完成局部放电信号降噪处理后，采用Duffing 振子和混沌理论完成局部放电过程中超高频信号的检测。在应用过程中，Duffing 振子是利用Duffing 方程完成混沌系统的描述，其公式为

式中：x 为降噪后局部放电时的混沌信号；（-x+x3）为混沌系统的恢复力；ω 为角频率；F 为策动力幅值；b为阻尼系数。

该算法在进行超高频检测过程中，如果混沌系统的阻尼系数值固定，则F 的值会超出设定阈值，以此会导致频率相同的信号之间敏感程度以及免疫特性增加。基于此可直接通过混沌系统的相变程度，检测局部放电过程中的超高频信号。如果混沌系统的相轨迹处于大周期临界状态，则将降噪后的局部放电信号输入混沌系统中，以此获取其初始策动力的信号敏感程度以及免疫水平，再利用相变程度检测局部放电过程中的超高频信号。

2 实验结果分析

以某地区的变压器作为测试对象，该变压器电压等级为360 V，其在运行过程中存在局部放电现象，对于变压器的安全运行造成较大影响。在该变压器上部署传感器采集局部放电信号，采集时间为连续10 天，共采集信号数量10000 万个，并将该信号作为测试信号。

随机获取2 种局部放电信号的采集结果，如图2 所示。依据图2 可知，本文方法应用后能够采集不同类别局部放电信号，并且采集的信号具有较好的连续性，没有发生信号损坏或者中断，信号的完整度较好。因此，本文方法具有信号采集能力，为局部放电过程中超高频信号检测提供数据支撑。

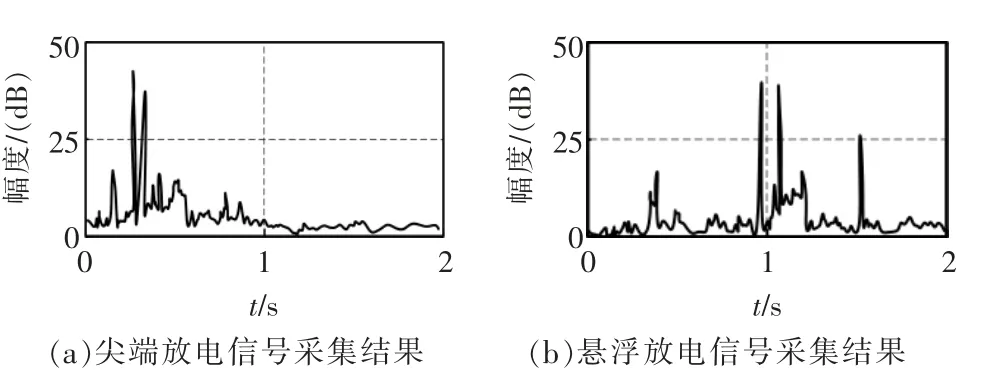
图2 信号采集测试结果Fig.2 Signal acquisition test results

随机选择一段采集的局部放电信号，采用本文方法对其降噪处理，结果如图3 所示。依据图3 测试结果可知，本文方法能够有效完成局部放电信号中噪声信号的处理，降低噪声对于信号的干扰，提升信号的效用率，以此提升超高频信号检测精度。

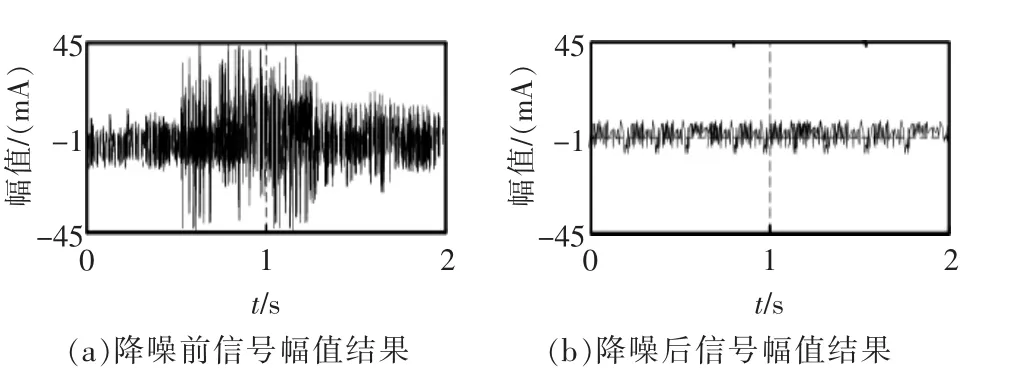
图3 信号采集测试结果Fig.3 Signal acquisition test results

为进一步验证本文方法的局部放电信号降噪效果，采用幅值误差ηi和波形相似度γi作为评级指标，两者的取值在0～1 之间，其值越大表示降噪效果越佳。在不同的局部放电信号数量下，对信号进行降噪处理后，ηi和γi的测试结果如表1 所示。依据1 结果可知，采用本文方法对局部放电信号进行降噪处理后，ηi和γi的结果均在0.927 以上，其中，ηi和γi的最大分别达到0.984 和0.988。

表1 幅值误差和波形相似度测试结果Tab.1 Results of the amplitude error and waveform similarity test

为验证本文方法对于局部放电过程中，超高频信号的检测效果，获取不同类别局部放电信号中超高频信号的检测结果，由于篇幅有限，结果仅呈现2种局部放电的超高频信号检测结果，如图4 所示。依据图4 测试结果可知，本文方法应用后能够精准检测不同类别局部放电过程中的超高频信号，精准呈现超高频信号的波动情况。因此，本文方法具有较好的应用性，满足检测需求。

图4 超高频信号检测结果Fig.4 UHF signal detection results

本文方法在不同的噪声比例下，对4 种局部放电过程中的超高频信号检测检测精度如表2 所示。依据表2 测试结果可知，在不同的噪声比例下，采用本文方法对4 种局部放电过程中的超高频信号检测精度均在92.5%以上，其中最高值达到99.3%，检测精度较高。

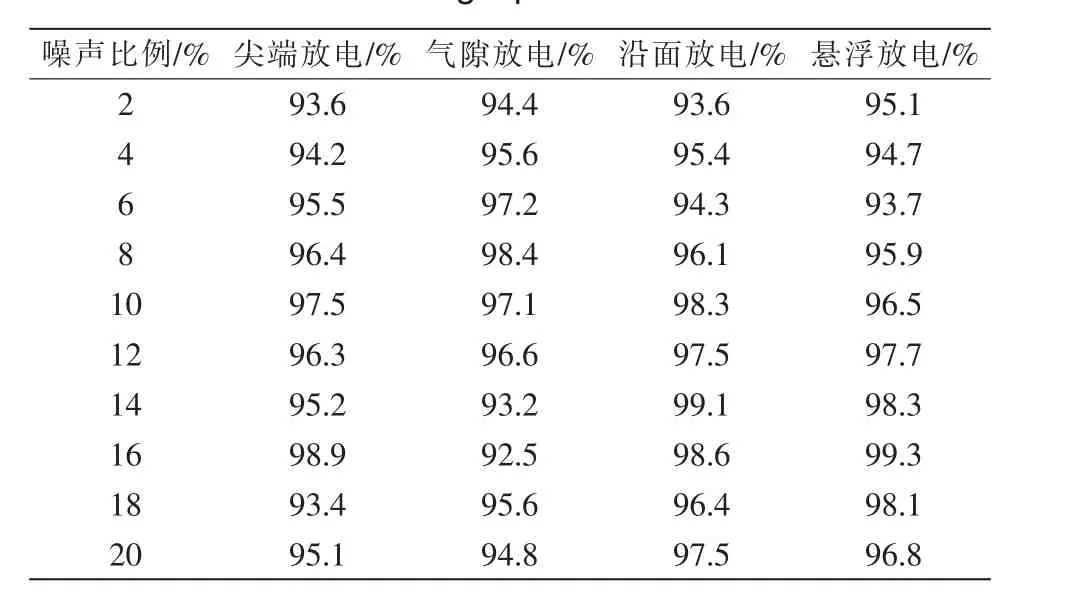
表2 4种局部放电过程中的超高频信号检测结果Tab.2 4UHF signal detection results during local discharge processes

3 结语

高压设备在运行过程中，局部放电会导致设备的绝缘体系受损，形成超高频信号，引起电力设备故障，直接影响电力系统的运行安全。因此为保证电力系统的运行安全，需精准检测超高频信号，判断绝缘缺陷，本文提出基于自适应小波去噪的局部放电超高频信号测量方式，完成超高频信号检测，并且检测精度较高，具有较好的应用性，可为电力系统运行管理提供可靠依据。