氢键流体中Janus粒子的过量熵

陈晴晴，李江涛，黄欣蓉，顾 芳，王海军，2，3

（1.河北大学化学与材料科学学院,2.河北省化学生物学重点实验室,3.药物化学与分子诊断教育部重点实验室,保定 071002）

Janus粒子是一种特殊的Patchy 粒子［1～4］，泛指同时具有两种不同性质的功能区域的胶体粒子.通常，两种功能区域的差异主要表现在几何结构、化学组成、亲疏水性、吸附性质、荷电种类及电负性大小等方面.在实验上，Janus粒子的这些性质可被有效地调控，从而使其在基础研究和实际应用中备受关注.研究表明，Janus粒子因其几何结构和物理化学性质的可控性可呈现出丰富的聚集态结构及相态结构，从而引发了非对称效应（结构和相互作用）在小尺度热力学方面的研究热点.同时，不同类型的Janus粒子在近年来已被广泛应用于油水分离［5，6］、水净化［7，8］、纳米材料［9，10］和催化［11，12］等多个领域，并取得了良好的效用评价［13］.

随着相关研究的不断深入，Janus粒子在溶液中的聚集态和相态结构已经引起了学者们的兴趣.这是因其聚集态和相态结构涉及到组装动力学和热力学、局域结构和整体性质、溶剂化力或排空势（Depletion potential）等［14～20］.这些内容均与溶液中Janus粒子的过量熵（Excess entropy）直接相关.鉴于此，定量化地研究Janus粒子在溶液中的过量熵问题具有重要意义［21～23］.本文以氢键流体中的Janus粒子为研究对象，在极稀溶液条件下，利用经典流体的密度泛函理论［24～32］研究氢键流体在其周围的局部结构，指出Janus粒子及氢键流体的相关特征对流体局域结构的影响.在此基础上，计算了Janus粒子的过量熵，并基于相关结果分析了Janus粒子与氢键流体之间的相互作用、氢键流体分子的官能度、氢键强度及体相密度等因素对过量熵的调控机制.

1 Janus粒子-氢键流体复合体系的经典密度泛函理论

为了探讨Janus粒子周围氢键流体的局部结构及相关性质，考虑Janus粒子与氢键流体混合后的溶液浓度极低，以致于Janus粒子之间的距离对各自周围氢键流体分布的影响可被忽略.这种稀溶液策略也是解释粒子间排空力和组装驱动力的有效途径之一［32～35］.相应地，Janus粒子与氢键流体分子之间的相互作用势［VEXT(r)］构成了流体分子的外势.依据经典流体的密度泛函理论［24～32］可知，体系以氢键流体分子数密度［ρ(r)］为变量的巨势泛函Ω[ρ(r)]可表示为

式中：F[ρ(r)]（J）为系统的内禀Helmholtz自由能；μ（J）为体系中氢键流体分子的化学势.

在式（1）中，F[ρ(r)]与粒子间的各种相互作用直接相关，通常可分解为理想部分FID[ρ(r)]和对应于各种相互作用的过量部分.对氢键流体而言，F[ρ(r)]的形式如下：

式中：FHS[ρ(r)]和FHB[ρ(r)]（J）分别代表粒子间的硬球作用和氢键作用对自由能的贡献.在基本度量理论（Fundamental measure theory，FMT）［23］和改进的基本度量理论（Modified fundamental measure theory，MFMT）［25，26］的框架下，可以明确给出硬球作用的泛函形式FHS[ρ(r)].FID[ρ(r)]和FHS[ρ(r)]的解析表达式已在本文支持信息中给出.

考虑AaDd型氢键流体系统（每个分子含有a个质子受体A和d个质子给体D），若n(r)为位置r处的局域氢键数密度，则氢键作用对自由能的贡献FHB[ρ(r)]为

式中：β-1≡kBT（kB是玻尔兹曼常数，T（K）是绝对温度；pA(r)和pD(r)分别定义为，表示质子受体A和质子给体D在位置r处的成键分数，二者满足描述氢键形成的质量作用定律［36］：

式中：εHB（J）为氢键键能；υ为形成氢键的成键体积参数；gHS[ρ(r)]为硬球流体的径向分布函数［27，37］.由于βεHB可以衡量氢键作用的相对强弱，因此被称作氢键强度参数，对应不同的氢键体系［38］.当体系处于平衡状态时，根据巨势函数最小化原理可得氢键流体分子的平衡密度分布为

式中：ρ为氢键流体的体相数密度；μEX（J）代表因粒子间的硬球作用和氢键作用所致的过量化学势，具体形式详见本文支持信息.

针对Janus粒子与氢键流体组成的稀溶液而言，将Janus粒子视为直径为σJ的球形粒子，同时，将AaDd型氢键流体分子视作直径为σ的球形粒子，且球面上分布着相应的质子受体和质子给体（图1）.

Fig.1 Schematic illustration of a Janus particle with diameter σJ immersed in a hydrogen bonding(HB) fluid of A2D2 type

鉴于Janus 粒子的几何特征，为了方便，在图1中构建了柱坐标系.相应地，直角坐标系中的点r（x，y，z）可转化为柱系坐标点r（q，z，ϕ），其中，.显然，Janus 粒子的柱对称性意味着ρ(r)可以简化为ρ(q，z)同时，将Janus粒子的两个半球面分别称作H 面（z>0）和L 面（z<0），它们的性质差异将依其所提供的外势加以区分.为此，除了考虑Janus粒子与氢键流体之间的体积排斥作用以外，进一步将其H 面和L 面对氢键流体的相互作用势VEXT(r)以Lennard-Jones势分别表示如下：

式中：Δ=(σJ+σ)/2；εH和εL（J）分别为Janus粒子的H面和L面对氢键流体的作用能.

综上，Janus粒子周围氢键流体的密度分布ρ(r)与氢键流体的官能度（a和d）、氢键强度βεHB、体相密度ρ、Janus粒子与氢键流体的尺寸比λ（λ=σJ/σ）、Janus粒子两面与氢键流体的作用强度βεH和βεL等因素直接相关.鉴于Janus粒子的柱对称性，在计算密度分布ρ(q，z)的过程中，首先，将空间变量q和z以σ为单位进行离散化（步长为0.01σ），进而利用标准的Picard迭代方法进行自洽求解，相应的判据为所有位置处的密度ρ(q，z)在前后两次迭代的差值均小于10-5.

在计算过程中，基于氢键作用与色散作用强弱的实际情况，选择εL=0.1εHB，同时将Janus粒子与氢键流体的尺寸比λ固定为2.为了表征Janus两面性质的差异，以H面和L面作用能之比γ（γ=εH/εL）作为参数，并在γ分别为0.5，0，-0.5 和-1 的情形下进行了相关的计算和讨论.显然，相对于L 面而言，参数γ的这些数值依次对应着H面为弱吸引作用、硬球排斥、弱排斥以及强排斥作用的情况.当获得氢键流体的密度分布ρ(q，z)以后，即可分析上述因素对流体局域结构的具体影响，进而计算Janus粒子的过量熵等热力学量.

2 Janus粒子周围氢键流体的局域结构

依据经典流体的密度泛函理论，通过计算不同参数下氢键流体的平衡密度分布ρ(q，z)，即可研究Janus 粒子周围氢键流体的局域结构.结果表明，氢键流体的官能度、体相密度、氢键强度、Janus 粒子与氢键流体分子的尺寸比以及两面的作用能等均可影响流体的局域结构.为了说明问题，图2给出了Janus粒子周围A2D2型氢键流体的密度分布情况（体相密度ρσ3=0.5，氢键强度βεHB=6），其中，Janus 粒子与氢键流体分子的尺寸比为λ=2，且Janus 粒子两面的能量比为γ=0（H 面为纯硬球作用）.

由图2 可见，Janus 粒子外围氢键流体的密度分布表明，H面和L面与氢键流体之间的相互作用差异对流体局域结构的影响非常显著.可以发现，H面外氢键流体的密度峰值明显低于L面上的密度峰值.这是由于H 面与流体分子间仅有硬球排斥作用，而L面与流体分子间还存在着吸引作用，致使氢键流体在L面一侧倾向于聚集.同时，H和L两个面外流体密度分布的振荡范围也明显不同，从而喻示着Janus粒子的两个半球面对流体的作用范围不同.此外，两个面外的氢键流体均呈现出层化（Layering）结构，这主要是因流体分子间的硬球作用和氢键作用的协同效应所致.

Fig.2 Density profile of HB fluid of A2D2 type around a Janus particle calculated under conditions of λ=2,γ=0,ρσ3=0.5 and βεHB=6

进一步选择不同的体相密度和氢键强度进行计算，即可得到相应条件下氢键流体的密度分布情况.与此同时，Janus粒子的作用可以通过改变参数γ进行研究.为此，可将参数γ分别选作-0.5和0.5（二者分别对应H面和L面与氢键流体作用性质的异同）.为了更加直观地说明问题，可以截取相应的密度剖面ρ(0，z)进行分析.基于计算结果，图3给出了氢键流体在不同体相密度时的密度剖面图.

Fig.3 Density profiles ρ(0,z) of HB fluid of A2D2 type around a Janus particle under various bulk density ρσ3

对比图3（A）和（B）的密度分布可见，Janus粒子在两个面上的性质差异可以显著地影响氢键流体的局域结构，具体表现为：（1）两个面外氢键流体的层化结构随体相密度的增加而逐渐明显，这主要是由于氢键作用与集体效应（密度）之间的竞争所致；（2）当γ=0.5 时，在中低范围的体相密度下（ρσ3≤0.6），L面外氢键流体的密度峰值总是高于H面上的峰值.但在较高的体相密度时，这种趋势则会发生逆转.然而，当两个面的相互作用性质改变（γ=-0.5）时，逆转趋势在中等密度时已然出现；（3）当γ=0.5时，H面和L面以外的氢键流体的局域结构基本相似，仅在幅度上存在差别.当γ=-0.5时，氢键流体在两个面外的局域结构（接触密度和峰形）已经明显不同.

鉴于氢键作用完全由氢键强度和官能度共同体现，因此，当固定流体的体相密度而改变氢键强度或氢键官能度时，可以明确氢键作用对Janus粒子球外氢键流体局域结构的调控机制.由于氢键强度和氢键官能度对密度分布的影响结果类似，为了简洁起见，仅给出氢键强度变化时相应的密度剖面ρ(0，z)（图4）.

Fig.4 Density profiles ρ(0,z) of HB fluid of A2D2 type around a Janus particle under various HB strength βεHB

不同氢键强度下的密度分布再次表明了Janus 粒子两面性质差异的显著作用［图4（A）和（B）］.具体表现为：（1）当γ=0.5 时，在中等以上的氢键强度（βεHB≥4）时，L 面外氢键流体的密度峰值总是高于H面的，且峰值差随氢键强度的增加而增加.当作用性质改变（γ=-0.5）时，这种趋势仅在氢键强度较高时才出现；（2）当γ=0.5时，H面和L面以外的氢键流体的局域结构基本相似，但幅度上存在差别.然而，当γ=-0.5时，氢键流体在H面外的局域结构则发生了实质性改变，且氢键强度越高，结构差异越大；（3）氢键流体的层化趋势随氢键强度的增加而逐渐弱化.对比H面和L面外的密度分布即可发现，当γ=-0.5时，层化趋势减弱得尤其明显，这是由于氢键作用与硬球作用的竞争所致.

以上氢键流体在Janus粒子外的密度分布表明，Janus粒子在两个面上的性质差异可以调控其周围氢键流体的局域结构，从而将影响体系在微纳尺度上的热力学性质.根据溶液的Kirkwood-Buff理论［39］可知，体系的一些热力学性质取决于相关物理量的涨落-关联性质（如粒子数涨落、密度涨落和内能涨落等）.在本质上，这些涨落均可通过密度分布或二体分布函数等进行研究.此外，利用氢键流体在Janus 粒子外的局域结构可以探讨Janus 粒子的过量熵、吸附性及其组装驱动力（排空势）等.可以预期，当Janus粒子的浓度增加时，其在氢键流体中的聚集态结构也将依赖于上述因素.

3 氢键流体中Janus粒子的过量熵

统计力学原理表明，熵与能量间的竞争作用是整个系统在相空间中演化的根源.在软物质领域中，有关体系聚集态结构和相态结构的研究已经充分揭示了熵的重要性［21，22，40，41］.如溶液中某些分子藉由排空力（Depletion force）驱动下的自组装行为在本质上是一个熵增过程.在热力学熵的若干贡献中，过量熵与流体局域结构相关，是表征流体或溶液体系局域结构的重要物理量.特别是在介观体系的物理化学现象中，过量熵的作用尤为突出.

当混合物中的化学组分在几何尺寸或相互作用存在明显差异时，过量熵的贡献主要来自两个方面：（1）当大尺寸粒子与小尺寸粒子混合后，体积排斥作用将导致小尺寸粒子运动相空间的显著减小；（2）大尺寸粒子间的有效作用（直接作用和因溶剂所致的间接作用）对流体局域结构范围的调控.因此，当粒子数密度较高（ρσ3>0.7）时，通常需要计算二体以上的相互作用［42～47］，以更加准确地预测体系的相关热力学性质.

对中低等密度的体系（ρσ3≤0.7），单粒子过量熵（S，以kB为单位）在准确到二阶近似时可表示为［40～45］

式中：g(r)表示以目标粒子为中心的二体分布函数（若其具有球对称性，则被称作径向分布函数）.对本文考察的体系而言，Janus粒子的特征决定了g(r)具有柱对称性，即，g(r)=g(q，z).因此，Janus粒子H面和L面的关联函数g(q，z)可依据z值的正负加以区分，由此可得：

在此基础上，结合式（8），并利用式（9）中的关联函数可分别计算H 面和L 面外的过量熵SH和SL以及Janus粒子的总过量熵值S（S=SH+SL），进而阐明相关因素的影响.

根据2 节中氢键流体的局域结构可知，体相密度和氢键强度是影响氢键流体密度分布的重要因素.为了阐明过量熵与体相密度和氢键强度等参数的依赖关系，计算了相关参数变化时的过量熵.为了简洁起见，图5给出了λ=2，γ=-1时的过量熵S.可见，在中低等体相密度的情形下，过量熵随氢键强度的增加而呈现轻微下降的趋势.然而，当体相密度增加时，过量熵则随氢键强度的增加而增加，且密度越高，增加趋势也愈加显著.同时，当氢键强度固定时，过量熵均随体相密度的增加而单调减小，且下降趋势在密度较低时更加明显.

Fig.5 Excess entropy of a Janus particle immersed in a HB fluid of A2D2 type under various bulk density ρσ3 and HB strength βεHB(γ=-1)

由式（6）和式（7）可知，Janus 粒子与氢键流体的相互作用仅在一定范围内影响氢键流体的局域结构，从而导致Janus 粒子的过量熵与其影响范围直接相关.在物理上，将Janus 粒子引入氢键流体以后，其体积排斥作用限制了氢键流体分子在相空间中的运动范围，从而导致了Janus 粒子过量熵的变化.过量熵在固定氢键强度时随体相密度的变化趋势反映了这一事实（图5）.此外，氢键强度对中低等体相密度下过量熵的影响并不明显，而当体相密度较高时却致使其随之增加而增加.这种变化趋势既表明了过量熵的主要贡献源自Janus粒子的体积排斥作用，也喻示了体积排斥作用与氢键作用之间存在竞争.一方面，当氢键流体的体相密度越低时，Janus粒子的体积排斥作用越弱，反之则越强.另一方面，氢键作用将在一定程度上平衡体积排斥作用，从而造成氢键强度越强而过量熵的降幅越小的变化趋势.

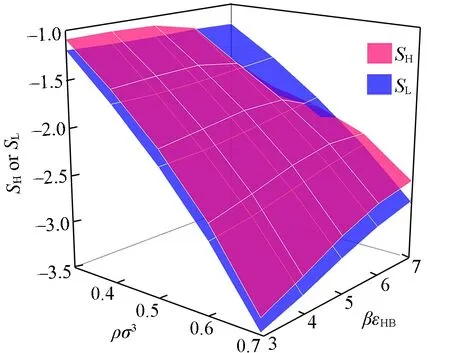
Fig.6 Excess entropies SH(red) and SL(blue) for H and L sides of a Janus particle immersed in a HB fluid of A2D2 type under various bulk density ρσ3 and HB strength βεHB(γ=-1)

为了进一步阐明Janus粒子两个半球面的性质差异对过量熵的具体影响，分别计算了不同条件下H面和L面的过量熵SH和SL.结果表明，SH和SL对各个参数的依赖性也能体现出两个面的性质差异.当两个面与氢键流体的作用性质相同而强度不同时，SH和SL的变化趋势大致相同.而当相互作用性质改变时，SH和SL之间则表现出明显差异.作为代表例证，图6给出了γ=-1时的相关结果.可见，SH和SL均随体相密度的增加而减小，但二者随氢键强度的变化却明显不同.当体相密度较低时，SH与氢键强度的依赖关系并不明显，但在中等体相密度以上，SH则随氢键强度的增强而显著增加.相反，SL在中低等体相密度时均随氢键强度的增加而呈现先增后降的变化趋势，而仅在高密度时随之单调递增.由此表明，Janus粒子两个半球面的性质差异对中低等密度的氢键流体具有明显的调控作用.

对于AaDd型氢键流体，分子间的氢键作用除了与氢键强度有关，也受到官能度a和d的影响.为了说明官能度对过量熵的影响，分别计算了A1D1，A1D2和A2D2型氢键流体相应的过量熵.鉴于官能度对过量熵在各个参数下的影响大致相同，仅给出在λ=2，γ=-0.5 及βεHB=6 的条件下过量熵与体相密度的变化情况，结果如图7 所示.可以看出，官能度越大，过量熵随体相密度增加所致的降幅也越小，这与氢键强度的影响基本类似.

以上结果表明，当在氢键流体中引入Janus 粒子后，将导致过量熵减小（S均为负值），且过量熵的降幅与体系的多个因素相关.当多个Janus粒子在溶液中发生聚集时，由此导致的整体熵变将表现为熵增加.因而，Janus粒子在溶液中的聚集在本质上是由熵所主导的热力学行为，即，熵是其聚集的主要驱动力.事实上，氢键流体中的Janus粒子之间除了直接相互作用，还有以溶剂为媒介所致的排空力（溶剂化力），而其物理实质则源自过量熵.同时，由于Janus的两个面在性质方面存在差异，所以它们对过量熵的贡献也大不相同.

Fig.7 Excess entropy of a Janus particle immersed in HB fluids of A1D1,A1D2 and A2D2 types at various bulk density ρσ3 under βεHB=6,λ=2 and γ=-0.5

4 结论

Janus 粒子在溶液中的聚集态结构和相态结构与Janus 粒子间直接作用和间接作用相关.针对由Janus粒子和氢键流体所形成的稀溶液，基于经典流体的密度泛函理论研究了以Janus粒子为中心的氢键流体的局域结构.作为应用，计算了氢键流体中Janus粒子的过量熵，进而明确了Janus粒子与氢键流体的相互作用、氢键流体的体相密度、氢键强度及氢键官能度等因素对过量熵的影响.计算结果定量地阐明了Janus 粒子两个性质不同的半球面对其过量熵及氢键流体局域结构的调控机制.可以预期，Janus粒子自身的特殊结构也将导致其物理性质方面的差异（如吸附性和排空势等）.在Janus粒子与氢键流体的溶液体系中，Janus粒子在结构和性质方面的对称性破缺可以通过其周围氢键流体的局域结构得以体现.同时，硬球作用和氢键作用等多种粒子间的相互作用也彼此竞争，导致了氢键流体局域结构随之变化.鉴于Janus粒子本身的特征，粒子聚集后能呈现出非常丰富的组装结构（微纳尺度上的多种斑图结构），这与Janus粒子间的有效相互作用直接相关.根据统计力学原理，当Janus粒子之间可以彼此影响或氢键流体的密度较高时，往往需要考虑到高阶相互作用（三体以上的作用）.此时，需要利用BBGKY 的级联方程或Kirkwood 的叠加近似等方法予以处理.因此，本文结果实际上是在中低等粒子数密度下的近似结果，而计入更加复杂相互作用的计算仍有待进行.

支持信息见http：//www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20230443.