坝口河沥青混凝土心墙坝三维地震响应分析

罗 林 范均勇 李金成

(昭通市水利水电勘测设计研究院,云南 昭通 657000)

土石坝地震响应分析方法通常有剪切梁法、集中质量法和数值方法三大类。其中剪切梁法[1]、集中质量法[2]为一维分析方法,前者将土石坝及坝基视为底端固定的变截面梁,采用解析方法获得地震响应,概念清晰;后者将土石坝简化为多质点体系进行分析,计算较为简单。上述两种方法的模型过于简化,对土体模量有限制,无法体现土石坝系统的地震响应。相比于一维简化分析的局限性,数值分析方法(包括二维和三维)能更真实地体现土石坝在地震作用下的响应[3-4]。

目前常用的数值方法有有限元法、有限差分法、边界元法、DDA法等。其中,有限元法能够合理考虑土石坝工程中复杂的边界条件、模拟土石坝工程中材料的力学特性等重要关键问题,处理非线性问题优势大且计算效率较高,在土石坝工程地震响应分析中占主导地位。

本文采用有限单元法对坝口河水库沥青混凝土心墙坝进行三维时程动力分析,以得到坝体在地震作用下的响应。计算中大坝静力计算采用邓肯-张非线性弹性模型,动力本构采用等效线性模型。

1 工程概况

坝口河水库位于云南省昭通市镇雄县东南部镇雄小河上游一级支流一头河干沟河段。大坝最大坝高71.40m,坝顶高程1609.20m,坝顶宽度10.0m,长度158m。按上游至下游的顺序,坝体分区由上游填筑区、过渡层、沥青混凝土心墙、过渡层、下游填筑区、排水棱体组成[5]。

2 计算模型及参数

2.1 软件参数

采用河海大学Autobank_3d[6]软件建立坝口河水库大坝的模型,并进行网格划分,见图1。模型中X、Y、Z三个方向分别为坝轴向指向左岸,顺水流方向指向上游、竖直向上。

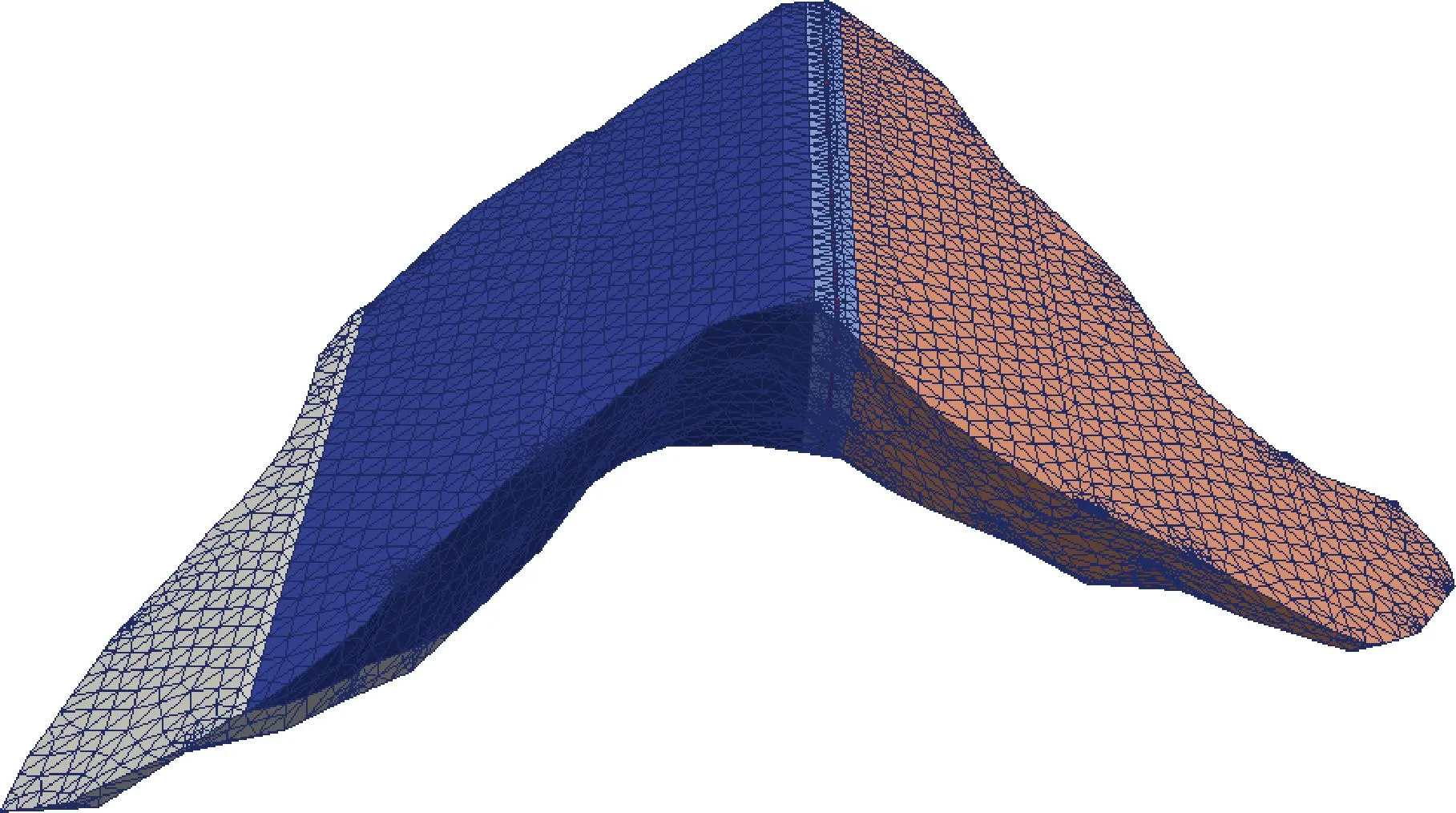
图1 坝体有限元计算模型

坝体动力响应计算工况取坝体正常蓄水位1605m。动力计算包含三个步骤:渗流计算、静力计算和时程法分析。其中静力计算以渗流计算为基础,得到的静力计算结果作为时程法分析的初始状态。渗流计算和静力计算参数根据试验数据确定,见表1。

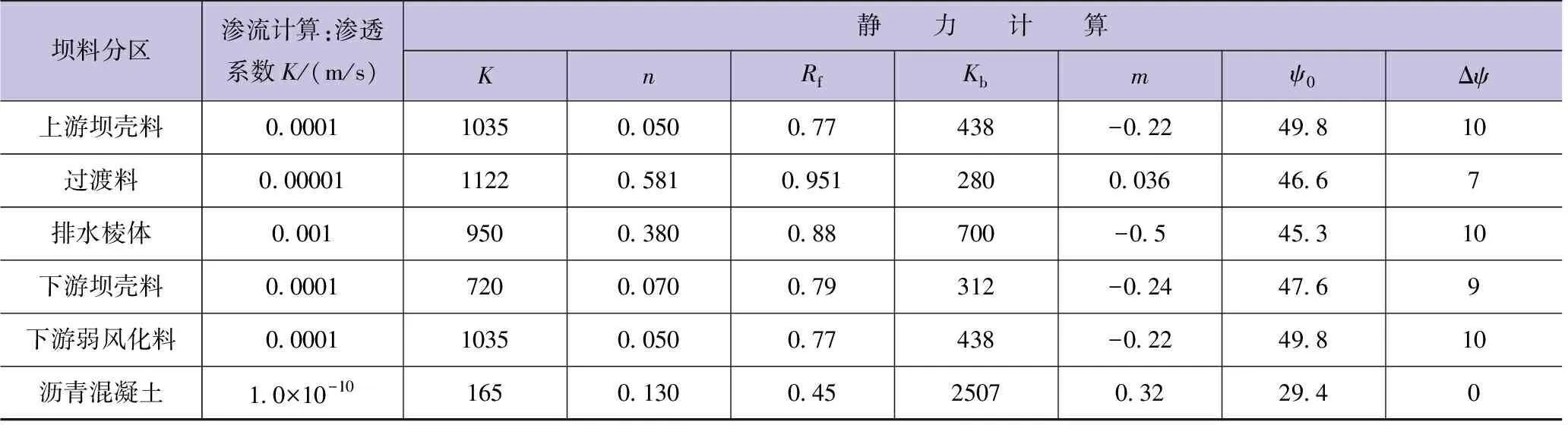
表1 渗流、静力计算参数

2.2 等效线性模型

当前岩土材料的动力本构模型可分为等效线性模型和基于弹塑性理论的真非线性模型[7]。真非线性模型能够合理地反映土体在不同应力状态下的应力变形规律,可以直接获取地震结束后大坝的整体变形,在理论上更为严谨。但真非线性模型的参数较多,试验复杂,计算量大,不利于开展大规模的数值计算。采用等效线性模型时,土体参数较少且获取方便,能够反映土石坝的地震响应规律,虽然不能反映地震过程中土体的变形,但等效线性模型的概念明确、应用简便、精度能够满足工程要求,并且等效线性模型在参数确定和工程应用方面积累了丰富的经验,在目前的土石坝有限元分析中仍最为流行。

等效线性模型通过迭代来近似反映土体的线弹性和非线性,由于每次迭代均为线性迭代,所以这种方法计算效率较高。对于大多数情况,尤其是应变较小(1%～2%),地震加速度小于0.3～0.4g的情况下都能提供较为合理的计算结果。

在等效线性模型中,土体的剪切模量G和阻尼比λ是剪切应变γ的函数,采用沈珠江院士提出的如下模型计算[8]:

最大动剪切模量计算式为

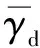
因此,采用等效线性模型计算的动力参数包括K1、K2、n以及动泊松比ν。参考同类工程的相关数据,本次坝口河水库大坝动力计算参数取值见表2。

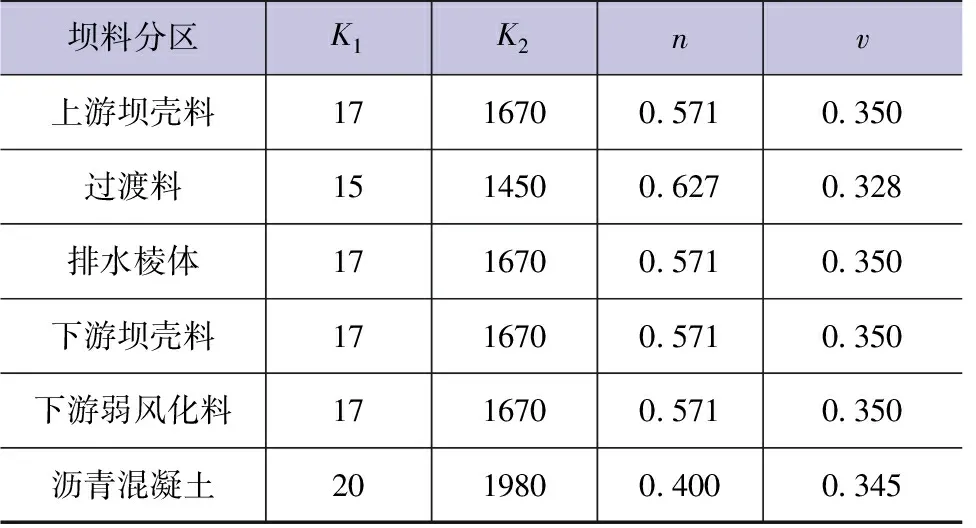
表2 坝体动力计算参数

2.3 地震波

根据《中国地震动参数区划图》(GB 18306—2015),工程区地震基本烈度为Ⅵ度,地震峰值加速度为0.05g,特征周期为0.45s。这里动力计算时将地震峰值加速度增大至0.10g,以探求该沥青心墙坝在地震作用下的响应。选取地震波,其峰值加速度为0.1g,特征周期为0.45s。计算地震波见图2。

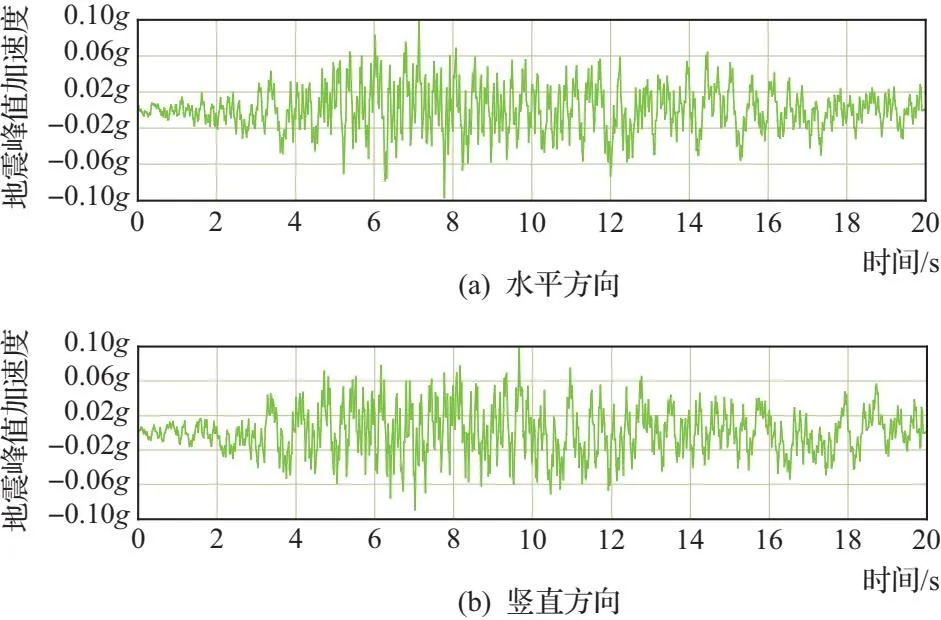
图2 计算地震波时程曲线

3 计算结果及分析

3.1 坝体的渗流及静力计算结果

如前所述,采用时程法计算之前需要得到坝体在正常蓄水位的渗流和静力状态。渗流计算浸润面(水头着色)见图3,上下游堆石体内浸润面几近水平,其消耗水头差较小,绝大部分水头消耗发生在沥青心墙内,符合沥青心墙坝渗流状态的特点。

图3 渗流计算浸润面

图4给出了坝体纵剖面主压应力云图,蓄水后下游侧过渡层底部出现了较大的压应力,整体上压应力成层分布。蓄水期坝体应力水平最大约为0.805,整体而言,蓄水期坝体仍处于三向受压状态。

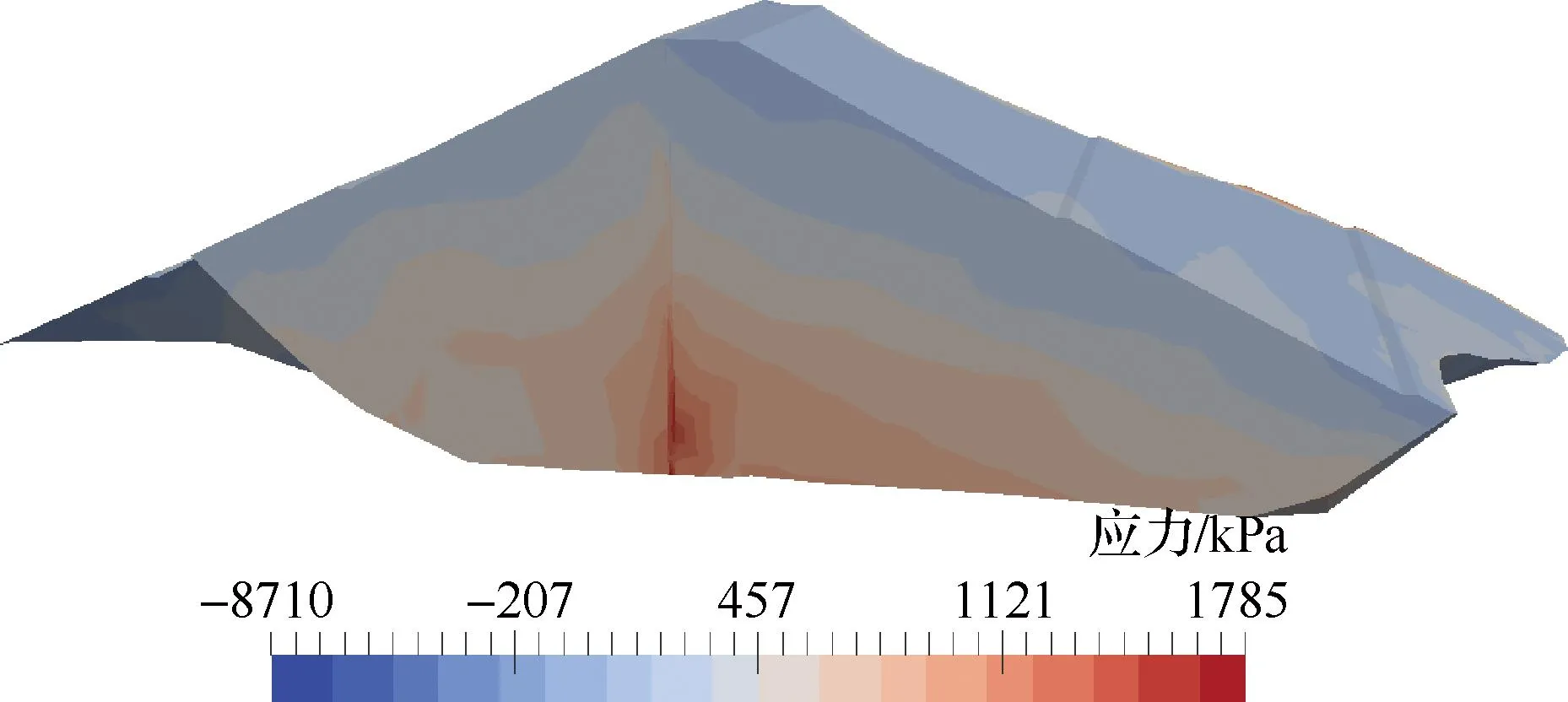
图4 主压应力云图

3.2 坝体的动力响应

3.2.1 模态分析

结构的自振周期反映了结构的动力特性,通常与坝体的体型、材料的刚度有关。采用等效线性模型分析坝体动力响应时,由于坝体的刚度还和振动的强弱有关,因此地震波也对坝体自振周期略有影响。

本文计算得到的一阶振型以顺河向变形为主(见图5),一阶频率为f=2.63Hz,对应周期为T=1/f=0.38s,约为0.53H/100,落在OKamoto给出的经验关系(0.35～0.65)H/100内,计算的结果正常[9]。

图5 坝体一阶振型

3.2.2 加速度

图6给出了坝体在地震荷载下的顺河向加速度最大值分布的平面图和剖面图。坝顶在振动过程中加速度最大值出现在坝顶中部,最大值为0.615g,但分布区域不大,仅在坝顶往下不到5m的区域,见图6(b)。地震过程中坝体顺河向加速度沿坝高放大,在同一坝体横剖面,位置越高,加速度越大,且增加速率明显,具有明显的“鞭梢”效应。由于坝口河水库大坝的地形特殊,坝体振动过程中未呈现明显的加速度在坝内向坝坡方向增大的现象。整体看,坝顶上、下游附近的区域加速度较大,易发生坝料松动,甚至滑落,建议上述区域采用适当的抗震加固措施。

图6 坝体顺河向最大加速度分布

图7给出了坝顶处监测点的动加速度时程线,相比于输入的地震波,坝顶处的加速度从频率上看更为均匀,也显示类似土石坝这样的土工结构在地震过程中有类似滤波器的功能。

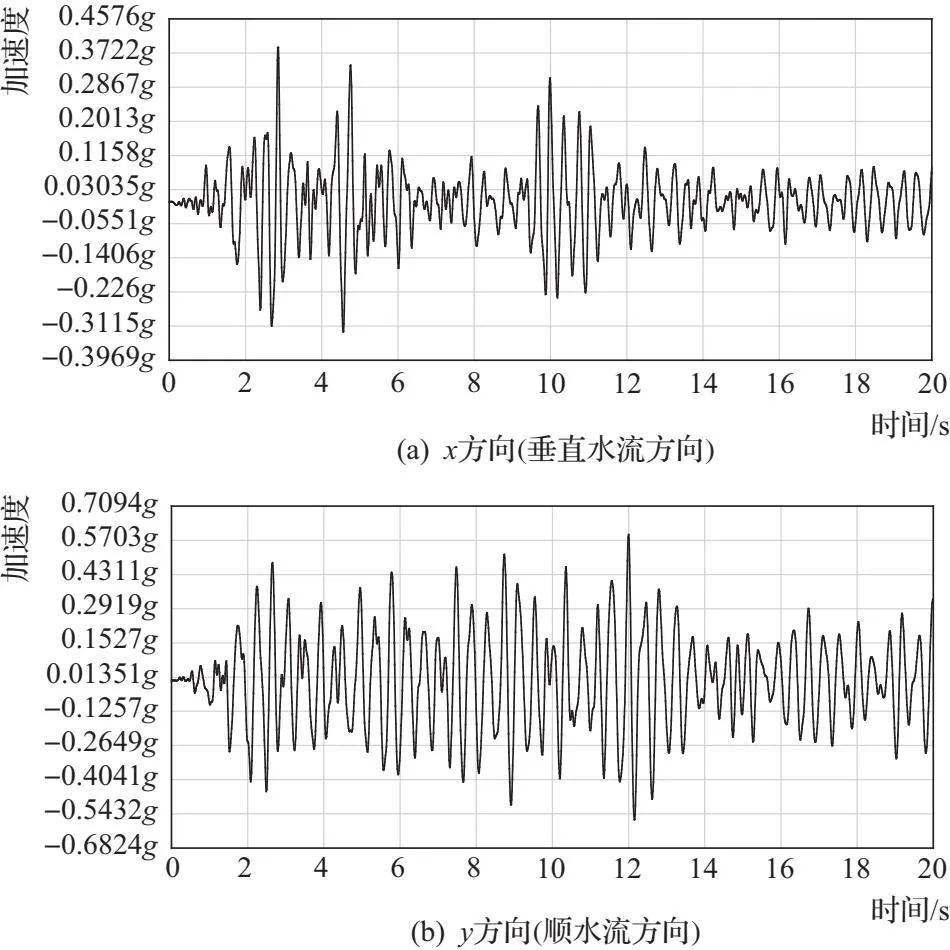
图7 坝顶监测点加速度时程曲线(一)

3.2.3 动位移

图8给出了坝顶监测点的相对动位移时程线。由于坝口河水库大坝体型特殊,振动周期较小,地震过程中坝体的振动幅度不大,相对动位移最大值约为12cm。

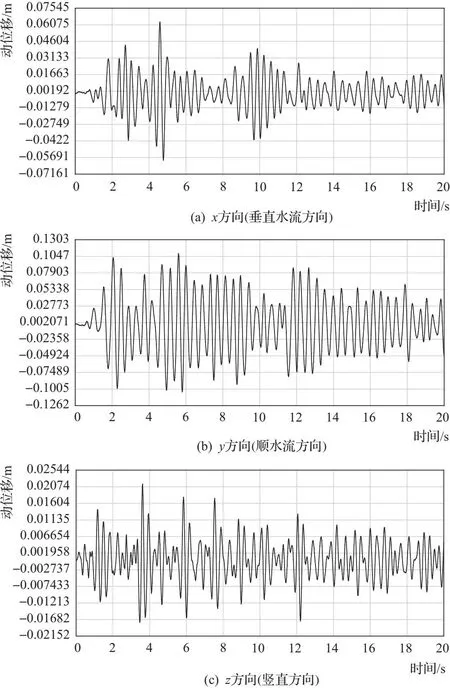
图8 坝顶监测点位移时程曲线

3.3 坝体永久变形

在地震的作用下,土工结构会产生永久变形(即不可恢复的残余变形)。由于土的弹塑性,产生的弹性变形在地震结束后即恢复,但产生的塑性变形在地震后不能恢复,造成坝体的永久变形或残余变形,影响其使用价值和外形美观,因此需要对坝体永久变形作定量分析,为抗震预留坝顶超高提供依据。

利用沈珠江提出的残余应变增量模型可以确定坝体单元各时段内的残余应变增量。模型中给出了残余剪应变增量和残余体积应变增量随振次的关系。

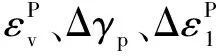
本次坝口河水库大坝的永久变形参数参考同类工程取值(见表3)。计算得到的坝体永久变形结果见图9。震动后坝体的垂直水流方向永久变形有:朝河谷中央方向,最大值为5.77cm;顺水流方向呈现上下游坝坡朝下塌落的趋势,约为13.12cm。竖向永久变形较大,达到24.63cm,出现在坝顶。通过与类似工程的对比分析可见[10],本文计算得到的地震永久变形分布规律、最大值发生的位置及变形值都是合理的,同时满足设计要求的坝体超高计算要求。

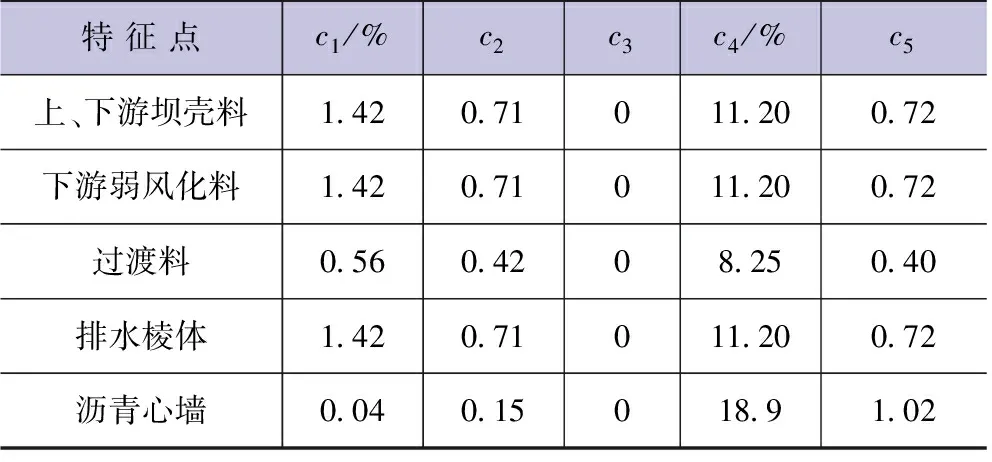
表3 永久变形计算参数

图9 地震永久变形计算结果

4 总 结

采用河海大学Autobank_3d软件对坝口河水库沥青混凝土心墙坝进行三维时程法动力分析,主要得到以下结果和结论:

a.坝体结构的一阶周期为0.38s,一阶振型以顺河向变形为主。

b.坝体顺河向加速度具有明显的放大效应,加速度最大发生在坝顶中部,最大值达到0.615g,但区域较小。此时坝顶上、下游可能出现坝料松动、滑落,建议该区域进行适当的抗震加固。坝体在震动过程中动位移最大值约为12cm。

c.地震后的永久变形以竖直方向为主,最大值约为24.63cm,满足设计预留的坝顶超高要求。

坝口河水库大坝位于河道拐弯处,上下游坝体均偏离坝体中轴线,体型较为特殊,动力计算结果也有其独特之处。本文计算结果可供类似工程参考。