TendiffPure: a convolutional tensor-train denoising diffusion model for purification

Mingyuan BAI, Derun ZHOU,2, Qibin ZHAO

1RIKEN AIP, Tokyo 1030027, Japan

2School of Environment and Society, Tokyo Institute of Technology, Tokyo 1528550, Japan

E-mail: mingyuan.bai@riken.jp; zhouderun2000@gmail.com; qibin.zhao@riken.jp

Received May 31, 2023; Revision accepted Jan.3, 2024; Crosschecked Jan.15, 2024

Abstract: Diffusion models are effective purification methods, where the noises or adversarial attacks are removed using generative approaches before pre-existing classifiers conducting classification tasks.However, the efficiency of diffusion models is still a concern,and existing solutions are based on knowledge distillation which can jeopardize the generation quality because of the small number of generation steps.Hence, we propose TendiffPure as a tensorized and compressed diffusion model for purification.Unlike the knowledge distillation methods, we directly compress U-Nets as backbones of diffusion models using tensor-train decomposition, which reduces the number of parameters and captures more spatial information in multi-dimensional data such as images.The space complexity is reduced from O(N2)to O(NR2)with R ≤4 as the tensor-train rank and N as the number of channels.Experimental results show that TendiffPure can more efficiently obtain high-quality purification results and outperforms the baseline purification methods on CIFAR-10, Fashion-MNIST,and MNIST datasets for two noises and one adversarial attack.

Key words: Diffusion models; Tensor decomposition; Image denoising

1 Introduction

Diffusion models (Dhariwal and Nichol, 2021;Gao et al., 2023) are ubiquitous in the recent three years in text, image, and video generation.They appeal to both academics and practitioners for their mode coverage, stationary training objective, and easy scalability.Among the generative models,compared with generative adversarial networks(GANs),as diffusion models do not require adversarial training, they are able to process a significantly larger range of distributions of features and hence avoid mode collapse.For the same reason, their training process is more stable than that of GANs.In terms of sample quality, diffusion models outperform variational autoencoders (VAEs) and normalizing flows(Ho and Salimans, 2021).They demonstrate strong capabilities as purification methods of removing both noises and adversarial attacks for data preprocessing,followed by the classifiers.

Benefiting from denoising score matching (Vincent, 2011) or sliced score matching (Song Y et al.,2020),diffusion models using score-based generative modeling methods are scalable to high-dimensional data in the deep learning settings.However, they still suffer from low sampling speed,which is caused by the iterative generation process.In specific, for each sampling or generation step,data are iteratively updated following the direction determined by the score until the mode is reached, where the score can be described by a score function.This score function is commonly approximated by a U-Net which is the backbone of a diffusion model.A large variety of data naturally possess multi-dimensional spatial structures, which can be easily neglected by convolution kernels of U-Nets (Ronneberger et al., 2015).U-Nets are the common backbone of diffusion models and in substance enable them to generate highquality images compared with other generative models, where nearly all U-Nets in pre-trained diffusion models have the same number of parameters,except a small number of them,such as U-Nets in denoising diffusion implicit models (DDIMs) (Song JM et al.,2021).Nevertheless, the large number of parameters in U-Nets still prevents diffusion models from achieving efficient generation and purification.

With the purpose of obtaining efficient and highquality purification and generation with diffusion models,a majority of existing solutions are in knowledge distillation (Meng et al., 2023; Song Y et al.,2023).For these methods, the goal is to reduce the number of iterative steps to accelerate the generation process, where the student models are diffusion models.In practice, a limited number of steps in the student models can hardly achieve the same performance as the teacher models (Song Y et al.,2023).These knowledge distillation methods did not consider the number of parameters or the multidimensional structural information in data.Hence,the qualitative performance of compressed models can easily be unrealistic.Besides, LoRA as a finetuning method for pre-trained diffusion models was recently proposed and it relies on matrix factorization, where the number of parameters was reduced and the two-dimensional structural information was tackled (Hu et al., 2022).However, when the pretrained diffusion models are unavailable or when there is complicated multi-dimensional structural information, LoRA will not be so effective and other methods are demanded.

Given the aforementioned problems in the scalability of diffusion models, we propose to compress diffusion models for purification and evaluate their performance on purification tasks.In specific, we design the tensor denoising diffusion purifier (TendiffPure), where we tensorize the convolution kernels in U-Nets using tensor-train (TT) decomposition(Oseledets,2011)as shown in Fig.1,enhancing or at least not jeopardizing the purification quality and reducing the space complexity fromO(N2) toO(NR2) with usuallyR ≤4 as the TT rank andNas the number of channels, especially for noisy or perturbed images (Li et al., 2019).This tensorization for compression distinguishes TendiffPure from knowledge distillation methods for diffusion models.We conduct three experiments on CIFAR-10 (Krizhevsky and Hinton, 2009), Fashion-MNIST(Xiao et al.,2017),and MNIST(LeCun et al.,1998)datasets separately,on two noises and one adversarial attack: Gaussian noises, salt and pepper noises,and AutoAttack (Croce and Hein, 2020).

2 Background

2.1 Diffusion models for purification

Fig.1 A brief summary of TendiffPure

Purification is to eliminate noises and adversarial perturbations in data using generative models before classification.Unlike other defense methods,purification does not assume the forms of noises,adversarial attacks, and classification models.Hence, generative purification models do not require retraining of classifiers and are not trained with threat models.Diffusion models as emerging generative models have been recently scrutinized for purification (Nie et al., 2022) due to their extraordinary generative power.They purify noised or adversarially perturbed data in two phases.First, in the forward process of diffusion models,Gaussian noises are iteratively added to the noised or adversarially perturbed data until they become Gaussian noises as well.Afterwards, in the reverse process, they are denoised iteratively to generate the purified data.Hence, the noises or adversarial perturbations are eliminated.Note that for datasets on which there are diffusion models pre-trained,we can directly use the pre-trained diffusion models for purification,and hence no training process is required.Besides, for those without pre-trained diffusion models, we need to first train diffusion models on clean, i.e., unperturbed, data, and then use these trained diffusion models for purification.

Diffusion models have been the prevalent generative model in recent years.They impress the machine learning and deep learning community with their powerfulness on sample quality, sample diversity, and mode coverage (Ho et al., 2020; Dhariwal and Nichol, 2021; Song JM et al., 2021; Vahdat et al., 2021).Benefiting from these advantages,they become appealing tools for purification, for example, DiffPure (Nie et al., 2022), where noises and even adversarial attacks in the perturbed dataxa∈Rd,xa～q(x) can be removed by diffusion models.The denoised or purified data should be as close to the clean datax ∈Rd,x～p(x)as possible.A typical diffusion model consists of two procedures:forward process and reverse process.The forward process progressively injects Gaussian noises to the data where the perturbed dataxaare diffused towards a noise distribution.For a discrete diffusion model, its forward process is formulated as

Instead of predictingμθ(xt,t), which is a linear combination of∈θ(xt,t) andxt, practically it is common to predict the noise component as part ofμθ(xt,t) using the noise predictor U-Net∈θ(xt,t)(Ho et al., 2020).θis the parameter for describing the mean and variance.The covariance predictorΣθ(xt,t) can be learnable parameters for enhanced model quality(Nichol and Dhariwal,2021).To thoroughly remove the noise or adversarial attack and keep the semantic information,Nie et al.(2022)proposed to add Gaussian noise int*∈(0,T]steps.

2.2 Tensor decomposition

Tensor decomposition and tensor networks are prevalent workhorses for multi-dimensional data analysis to capture their spatial structural information,to reduce the number of model parameters,and to avoid the curse of dimensionality issue, including images (Luo et al., 2022).Here we refer to a multidimensional array as a tensor, where the number of“aspects” of a tensor is its order and the aspects are the modes of this tensor;for example,a 1024×768×3 image is a 3rd-order tensor with the sizes of mode 1,mode 2, and mode 3 being 1024,768, and 3, respectively.The key of tensor decomposition and tensor networks is to dissect a tensor into the sum of products of vectors as CANDECOMP/PARAFAC(CP)decomposition(Carroll and Chang,1970),matrices and tensors as Tucker decomposition (Hitchcock, 1927; Tucker, 1966), small-sized tensors such as TT decomposition (Oseledets, 2011) and tensor ring decomposition (Zhao et al., 2016), and tensor networks such as multi-scale entanglement renormalization ansatz (MERA) (Giovannetti et al., 2008).Among them, TT decomposition demonstrates its prevalence in a number of deep learning models for compression because of its low space complexity and capabilities of improving the performance of deep learning models (Su et al., 2020).In specific, TT decomposition considers aDth-order tensorY ∈RI1×I2×···×IDas the product ofD3rd-order tensorsXd ∈RRd-1×Id×Rd,d= 1,2,···,D, with the rankRdmuch smaller than the mode sizeId:Y=X1×13X2×···×13XD.Here,Xd×13Xd+1is the contraction of mode 3 ofXdand mode 1 ofXd+1.Note that forX1andXD,R0=RD=1.

3 Tensorizing diffusion models for purification

As aforementioned,we aim to compress the diffusion models from the perspective of reducing the parameter size,at least to attain similar performance of the uncompressed diffusion model on image denoising and purification tasks, i.e., using generative models to remove perturbations in data including adversarial attacks.Therefore, we propose Tendiff-Pure which is a convolutional TT denoising diffusion model.

In each step of a generic diffusion model as in Eqs.(1) and (2), the key backbone is the U-Net∈θ(xt,t) in the reverse process.Hence, it provides the potential to compress the diffusion models by reducing the number of parameters of the U-Net.Note that the U-Net at each step of the reverse process shares the same parameters.For the U-Net∈θ(xt,t),we compress it as

For ConvTTUNet(xt,t), each convolution kernel is parameterized using TT decomposition.In existing diffusion models, U-Nets often employ 2Dconvolution kernels,where each convolutional kernel isWi ∈ROi×Ci×Ki×Di, whereOiis the number of output channels,Ciis the number of input channels,Kiis the first kernel size,andDiis the second kernel size.In TendiffPure, we decompose these 4th-order tensors into the following TT cores:

whereU1∈R1×Oi×R1,i,U2∈RR1,i×Ci×R2,i,U3∈RR2,i×Ki×R3,i, andU4∈RR3,i×Di×1as demonstrated in Fig.2.This parameterization follows the standard TT decomposition in Section 2.2, whereR0,i=R4,i= 1.Hence, the space complexity is reduced fromO(N2)toO(NR2).

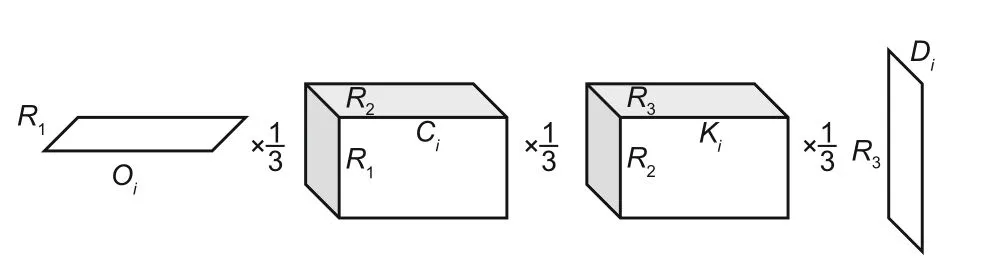
Fig.2 Convolution tensor-train kernels of Tendiff-Pure

Practically,R0,ican equal the number of input channels.Hence, we have parameterization of U-Nets as

whereU1∈ROi×Ci×R1,i,U2∈RR1,i×Ki×R2,i, andU3∈RR2,i×Di×1.We allow for a more generic parameterization,where the convolution kernels are decomposed into two TT cores,i.e.,

withU1∈R1×Oi×Ci×Ki×R1,iandU2∈RR1,i×Di×1.Note that for all three decomposition schemes, the convolution kernelsWiare squeezed to remove the modes with size 1 for programming.We design these three decomposition schemes to enable a wider range of choices of ranks of TT cores, as the performance of the decomposed model can be sensitive to the ranks of parameters, and we aim to attain the optimal ranks.At the end, each convolution operation in the convolutional TT U-Nets is defined as

where“⋆” represents the convolution.

Building on these convolutional TT U-Nets as backbones,the proposed TendiffPure is in substance a convolutional TT denoising diffusion model.We follow the general architecture of the denoising diffusion probabilistic model (DDPM) to remove the perturbations,including the adversarial attacks.Instead of completing the forward process,we add only Gaussian noises until stept*, wheret*＜T, inspired by Nie et al.(2022).Hence, we can control the amount of Gaussian noises added to ensure that the perturbations can be properly removed and that the semantic information is not destroyed in the denoised or purified images.In our case, we use the search methods to find the optimalt*.These search methods include the commonly applied grid search and random search for hyperparameter tuning.For the experiments,we use grid search to seekt*for its simplicity.

Furthermore, we recognize that low rankness might be related to the robustness of diffusion models (Nie et al., 2022).In particular, according to Theorem 3.2 in DiffPure (Nie et al., 2022), thel2distance between the clean dataxand the purified data ˆx0is

4 Experiments

4.1 Experimental settings

4.1.1 Datasets and network architectures

With the purpose of investigating the numerical performance of the proposed TendiffPure, we implement experiments on three datasets: CIFAR-10 (Krizhevsky and Hinton, 2009), Fashion-MNIST(Xiao et al.,2017),and MNIST(LeCun et al.,1998).After conducting the purification or denoising tasks,we intend to investigate if the purified images by the models are close to the clean images enough.Hence,we harness the pre-trained classifiers ResNet56 and LeNet,where ResNet56 is for the CIFAR-10 dataset and LeNet is for the Fashion-MNIST and MNIST datasets.Then we use them to classify the purified or denoised images.If the purified or denoised images can be classified into their original classes by the classifier,it is quantitatively close enough to the clean image.Note that for all the diffusion models in our experiments,we employ the classifier guidance.

4.1.2 Noises and adversarial attacks

We add two different noises,Gaussian noise and salt and pepper noise (S&P noise), and one adversarial attack, AutoAttack, to each of CIFAR-10,Fashion-MNIST, and MNIST datasets.The Gaussian noise level is 51,whereas the proportion of S&P noise added in images is 15%.In terms of the adversarial attack,AutoAttackℓ2threat models are commonly used (Croce and Hein, 2020).Here we use the STANDARD version of AutoAttack.It consists of APGDCE(which does not have random starts),the targeted version of APGD (APGDT) as the difference of logit ratio loss handling a model with a minimum of four classes, the targeted version of the FAB attack (FABT), and the Square Attack as a score-based blackbox attack for norm-bounded perturbations.In practice, the STANDARD version AutoAttack actually makes stronger attacks (Nie et al., 2022).For AutoAttack, we evaluate Tendiff-Pure against theℓ2threat model with∈=0.5.

4.1.3 Baselines

We compare our proposed TendiffPure with two other diffusion models,DDPM (Ho et al.,2020)and DDIM (Song JM et al., 2021), which are the core of nearly all existing diffusion models.Note that we employ two settings of the diffusion timesteps for DDPM and DDIM ast*∈N+(t*≤T) andT, and we present the better results between the two settings.The reason is that we aim to follow the vital diffusion model for purification, DiffPure,where the amount of Gaussian noise is carefully chosen to ensure that the noise or adversarial attacks in the images can be eliminated and that the label semantics of the purified images is not destroyed.As the discrete version of DiffPure is DDPM with the diffusion timestept*,we emphasize DDPM as a discrete DiffPure in the experimental results if its performance under settingt*is better than that underT.

4.1.4 Evaluation criteria

1.Quantitative criterion

The quantitative evaluation metrics are the standard accuracy, which measures the generative power, and the robust accuracy, which shows both the generative power and the robustness of purification models.To obtain the robust accuracy, the perturbed and adversarial examples are the input of purification models.Once the purification models produce the purified data,these purified data are classified by the classification models whose output is the classification accuracy, i.e., the robust accuracy.To obtain the standard accuracy,it follows the same procedure as what is for the robust accuracy,except that the input data of purification models are clean data without adding noises or adversarial attacks.For the quantitative results,we run the experiments multiple times.Then we report the average standard accuracy and robust accuracy with their error bars.We use the aforementioned classifiers to test if TendiffPure is able to sufficiently remove the noises and adversarial attacks and meanwhile preserve the label semantics of images with the reduced number of parameters compared with the baselines.

2.Qualitative criterion

The performance of TendiffPure is also evaluated in the qualitative perspective.Whether as a human we agree the purified or denoised images by TendiffPure to be more realistic than those purified by the baselines is a vital criterion to evaluate the performance of TendiffPure.Hence, we present the purified images by TendiffPure.Those generated by DDPM witht*as discrete DiffPure orTas DDPM of purification are presented,where the images with the higher quality are selected.Note that we decide not to present the results generated by DDIM, because of its incapability of removing the noises and adversarial attacks, even compared with DDPM.This is indicated in the quantitative results.

4.2 Experimental result analysis

4.2.1 Quantitative result analysis

1.Comparison with baselines

To begin with, we scrutinize the quantitative performance of TendiffPure compared with those of the baseline models.As aforementioned, a higher robust accuracy produced by the pre-trained classifier ResNet56 or LeNet indicates that the denoised or purified images are closer to the clean images.Table 1 demonstrates that for the CIFAR-10 dataset,the proposed TendiffPure outperforms the baseline diffusion models on the Gaussian noise, S&P noise,and AutoAttack.It also shows that the TT parameterization in TendiffPure successfully captures the multi-dimensional spatial structural information in images and enhances the performance of diffusion models in denoising and purification tasks, along with the reduction of the number of parameters.We can draw the same conclusions from the results on the Fashion-MNIST dataset(Table 2).However,for the results on the MNIST dataset demonstrated in Table 3, TendiffPure produces the purified images with the highest quality in terms of the classification accuracy, except the robust accuracy under Gaussian noises where DDPM (DiffPure) ranks the first.The possible reason is that tensor decomposition methods prefer spatially complicated data, whereas the MNIST dataset contains only handwritten digits with simple spatial information compared with Fashion-MNIST and CIFAR-10 datasets.

2.Ablation studies

We are interested in the effect of TT ranks,i.e.,Rd,i’s, on the purification or denoising results, because they can reveal how much compression can be beneficial to the purification or denoising performance of TendiffPure.Tables 4-6 indicate that TendiffPure prefers TT parameterization as in Eq.(5)with a smaller number of parameters reduced, in specific, with the compression rates being 44.29%,22.78%,and 22.78%for CIFAR-10,Fashion-MNIST,and MNIST respectively, where the compression rates are computed as the number of parameters of TendiffPure divided by the number of parameters of DDPM (DiffPure).It unveils that in practice,it may not be beneficial to dissect the convolution kernel in terms of the product of the numbers of input channels and output channels,for purification or denoising tasks.We observe that the ranges of thestandard accuracy and the robust accuracy among different TT ranks are larger than the difference between those of DiffPure and TendiffPure with the optimal TT ranks.For all three datasets, TendiffPure has the lowest standard accuracy and robust accuracy at rank(3,3,3)according to ablation studies in Tables 4-6, where TendiffPure performs worse than DiffPure using either DDPM or DDIM.It is possible that the effect of TT parameterization is sensitive to the TT ranks, which can significantly affect the robustness of diffusion models.In specific, the lowest standard accuracy and robust accuracy often occur at the higher TT ranks, which can be an interesting finding about the relationship between low rankness of parameters and robustness of diffusion models.In conclusion, these findings can pave the way for our future study on theoretically analysis of how to decompose convolution kernels using tensor decomposition or tensor networks to compress U-Nets in diffusion models properly.

Table 1 Purification performance of TendiffPure on CIFAR-10 evaluated by the pre-trained ResNet56 classifier

Table 2 Purification performance of TendiffPure on Fashion-MNIST evaluated by the pre-trained LeNet classifier

Table 3 Purification performance of TendiffPure on MNIST evaluated by the pre-trained LeNet classifier

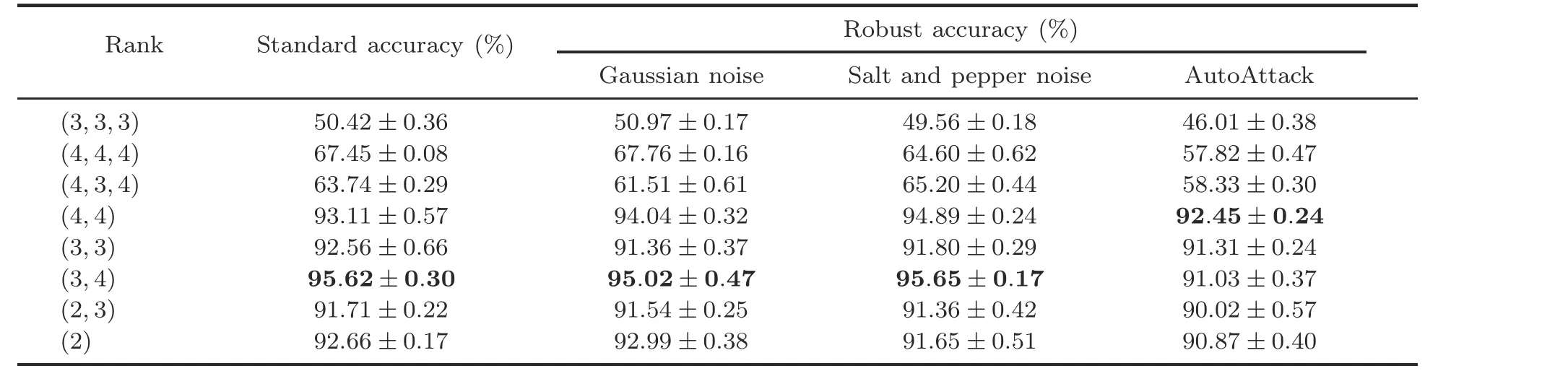
Table 4 Ablation studies of TendiffPure on CIFAR-10 evaluated by the pre-trained ResNet56 classifier

Table 5 Ablation studies of TendiffPure on Fashion-MNIST evaluated by the pre-trained LeNet classifier

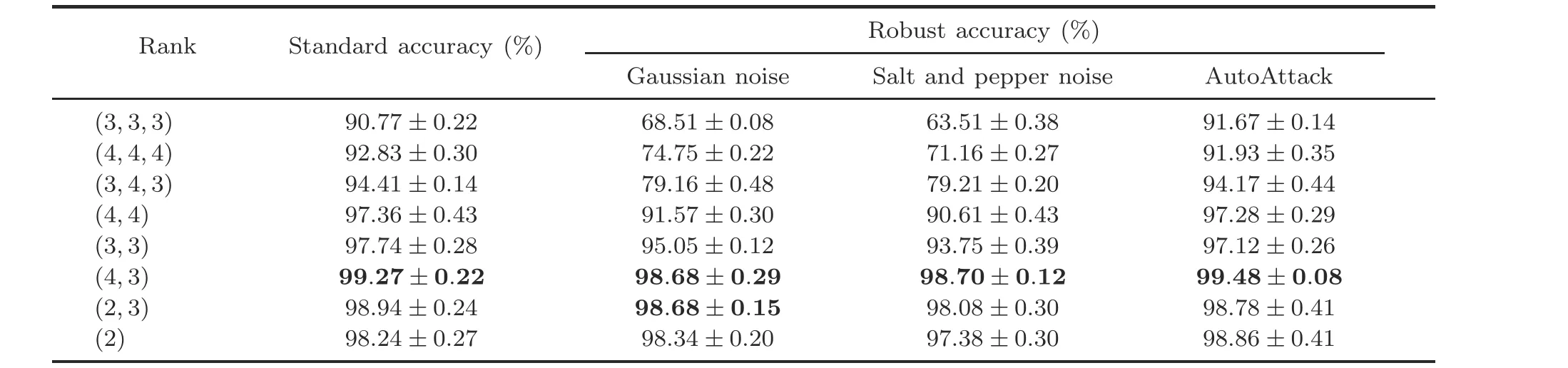
Table 6 Ablation studies of TendiffPure on MNIST evaluated by the pre-trained LeNet classifier

4.2.2 Qualitative result analysis

As for the qualitative performance of Tendiff-Pure, we present the purified or denoised images as a subset of the purified or denoised CIFAR-10 dataset on Gaussian noise, S&P noise, and Auto-Attack.In Fig.3, TendiffPure generates evidently more realistic images which are closer to the original images, i.e., clean images.In specific, DDPM as a discrete DiffPure even produces an image of a dog with two heads in the third row and second column of Fig.3c.For the case with S&P noise as shown in Fig.4, although DDPM (DiffPure) and Tendiff-Pure both demonstrate their limitations on removal of noises added on structurally complicated images such as toads and frogs, TendiffPure still preserves more structural information with a largely reduced number of parameters and possesses more robustness.It is consistent with the qualitative performance of TendiffPure for AutoAttack perturbed on the CIFAR-10 dataset.TendiffPure also eliminates this adversarial attack and generates images with more realism than DDPM (DiffPure) as in Fig.5.

5 Conclusions

Fig.5 Selected purified or denoised images by TendiffPure on the CIFAR-10 dataset with AutoAttack compared with DDPM (DiffPure): (a) original images; (b) AutoAttacked; (c) DDPM (DiffPure);(d) TendiffPure

To enhance the efficacy of diffusion models in purification, we propose TendiffPure as a diffusion model with convolutional TT U-Net backbones.Compared with existing methods,TendiffPure largely reduces the space complexity,and is able to analyze spatially complicated information in multi-dimensional data such as images.Our experimental results on CIFAR-10, Fashion-MNIST, and MNIST for Gaussian and S&P noises and AutoAttack show that TendiffPure outperforms existing diffusion models for purification or denoising tasks,quantitatively and qualitatively.

However, there are still potential limitations of TendiffPure.At this stage, how the TT ranks affect the purification or denoising performance is not theoretically studied.Hence, other than grid search,there is no better method to provide an optimal scheme to decide how to decompose the convolution kernel in U-Nets as backbones of diffusion models using TT decomposition or even tensor decomposition or tensor networks.In the future work, we aim to theoretically analyze the effect of tensor decomposition methods on diffusion models for purification.

Contributors

Mingyuan BAI designed the research.Derun ZHOU processed the data.Mingyuan BAI drafted the paper.Qibin ZHAO helped organize the paper.Mingyuan BAI and Derun ZHOU revised and finalized the paper.

Compliance with ethics guidelines

All the authors declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.