FFT 和MEM 在冲击回波法识别混凝土缺陷尺寸中的对比研究

杨海林

（唐山工业职业技术学院，河北 唐山 063299）

0 研究背景

冲击回波法（IMPACT-ECHO-METHOD）诞生于美国的康奈尔大学(Cornell University)，是Sansalone M 和Carino N J 在大量试验的基础上于1986 年正式命名的一种新型无损检测法，简称IE。IE 法由于自身较强的抗干扰能力和高分辨率，自诞生之日起就引起了工程检测领域广泛的关注，是一种识别混凝土内部缺陷的理想方法，前景广阔。经过多年的发展，冲击弹性波检测仪器目前已经国产化，为混凝土缺陷的识别提供了强有力支撑。冲击回波法有效识别混凝土缺陷的关键在于波形信号的处理，当前流行的信号处理方法有FFT 和MEM。

查阅大量关于MEM 和FFT 应用于冲击回波信号处理的文献，发现当前的研究主要有：柴文浩[1]等建立了有限元模型和物理试验模型，通过冲击回波试验对灌浆缺陷进行了识别，对经过FFT 后的信号进行了分析，发现FFT 可以识别缺陷的特征频率，但抗干扰能力差，信号中的各种特征峰值相互重叠，给缺陷识别带来干扰。舒志乐[2]等针对无砟轨道砂浆层的缺陷进行了有限元仿真和现场试验，应用MEM 对检测信号进行了处理，生成了缺陷云图，比较准确地识别到了缺陷的位置，但研究方法单一，缺少对比验证。黄维[3]以某实际装配式建筑为例，应用MEM 对灌浆套筒的冲击回波信号进行了解析，发现应用MEM 可以得到缺陷附近波速，通过反射波速与标定波速的差值判断灌浆情况，不足之处在于灌浆料强度不足同样会导致波速降低，没有进行FFT 和MEM 的对比分析。姜勇[4]等针对隧道衬砌缺陷进行了冲击回波测试，生成了MEM 云图，发现应用MEM 得到的结果更加直观，能准确反映缺陷的位置，但没有对缺陷尺寸进行定量研究。耿豪[5]等针对单排双排灌浆套筒的内部缺陷进行了冲击回波测试，通过MEM 法获得波速，通过FFT 获得卓越频率，对比分析后准确判定了缺陷的位置，能够有效评估灌浆质量。

信号处理是冲击回波测试的核心问题，查阅文献[6-10]，总结已有的研究成果，发现MEM 和FFT在冲击回波检测混凝土缺陷的信号处理过程中都有应用，但对于两种方法的对比分析研究成果不丰富。基于此，文章对FFT 和MEM 的基本原理进行归纳，对预先设置缺陷的混凝土模型进行冲击回波测试，分析两种方法的测试结果，对检测效果和精度进行分析，为后续研究提供了一定基础。

1 FFT 理论

1.1 傅里叶理论概况

对于冲击回波信号，有时域表示法和频域表示法。时域图中横轴为时间纵轴为幅值，可以用示波器实时记录位移信号随时间的变化，采样完成后进行时域分析。频域图中横轴为频率纵轴为幅值，是时域信号经过傅里叶变换得到的结果，表示频率随时间的变化，求得频谱的过程称为频域分析。由于时域信号较复杂，无法快速获得关键信息，而频谱图中可以展示混凝土结构厚度和内部情况的关键频率，所以处理冲击回波信号的关键在于能否对波形进行时频转换得到频谱，傅里叶变换就是一种可行的手段。

下面以某信号为例详细阐述时频转换，见图1。图1（a）中，能看到波形信号随时间的变化趋势及幅值，但无法直观地提供各个信号分量的信息。图1（b）中，能看到转换后的频域图，从图中可以观察到两个明显峰值，携带的关键信息可以从图中直接观察到，对于检测结果的分析非常方便。

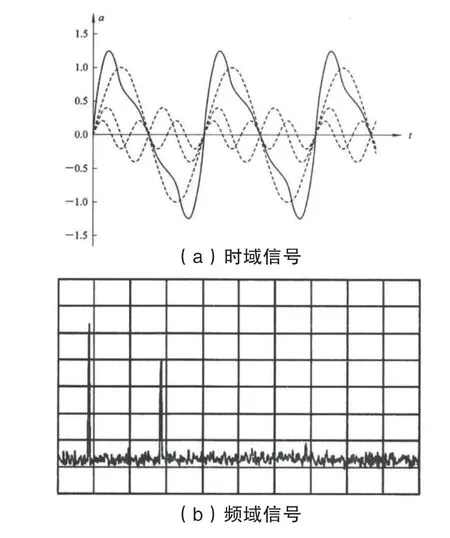
图1 某信号时频转换

既然时域和频域都可以表示同一个信号，那么他们之间是如何转换的呢？这里就要用到傅里叶变换，傅里叶理论认为，波形信号可以看作是由一个或数个频率不等的幅值和相位组成的正弦波，要想完成转换，信号在（-∞，+∞）就必须是完整的，但实际工程中只能进行有限周期内的测量，所以变换结果会产生一定的误差。傅里叶变换既可以表示离散频率也可以表示连续频率，傅里叶逆变换还可以将频谱转换为波形，定义时域和频率对应的表示为傅里叶变换对，其中每个时域只对应一个频域，保证解的唯一性。

1.2 FFT 理论概况

传统的离散傅里叶变换（DFT）可以完成波形信号的数字化，从而得到频域图形，是信号分析领域一种比较常用的方法。通过离散傅里叶变换和离散傅里叶逆变换可以实现时频信号的互相转换，并且其特性和连续傅里叶变换极其接近，为后续处理连续信号提供了基础，但缺点是运算量太大，实际工程中不易实现。假设取样数为N，应用DFT 的运算次数需要达到N2，如此大的运算量即使借助计算机也是很困难的。基于此，就产生了一种依托计算机技术的快速傅里叶变换方法（Fast Fourier Transform，以下简称FFT），FFT 最早于1965 年被J. W. Cooley 和J.W. Tukey 提出，之后得到了快速发展[11]。当取样数为N时，对于FFT 需要的运算次数就变为Nlog2N。

下面以实际数据对DFT 和FFT 的运算效率举例说明，由于计算机执行二进制运算法则，可以假设取样长度为210（即1 024），那么DFT 所需的运算次数为1 0242（即1 048 576），而FFT 只需要达到1 024log21024（即10 240），运算量减少了近一百倍，意味着完成相同的时频转换，FFT 只需要消耗相对于DFT1% 的时间和资源，所以FFT 目前被广泛应用于频谱分析。

FFT 应用较早，是传统的频谱分析方法，计算简单快速。理想状态下FFT 适用于整个时域，但实际检测过程中采样时间是有限的，只截取了部分信号来代表整体，这会导致频谱泄漏和峰值加宽，实际检测中可以通过添加窗函数来减少泄漏，但会降低频谱分辨率。

2 MEM 理论

2.1 MEM 理论概况

求解冲击回波信号的核心包括3 个方面，即存在性、稳定性以及唯一性，3 个条件必须同时满足才能得到准确解，但实际工程中的检测数据通常是不完整的，周围环境也可能存在噪声，经常出现不能满足其中某个条件的情况，把这类情况定义为不适定问题（Ill-Posed Problem）。当求解此类问题时，解通常不唯一，通过统计方法找到可能性最大（即熵最大）的那个解，就是最大熵法（Maximum Entropy Method，以下简称MEM）。MEM 是1967年J. P. Burg 在研究地震波的过程中首先提出的，之后在1971 年被A. van Den Bos 证明了其应用效果[12]。

应用MEM 时要注意以下3 个方面：1）MEM求解时，存在性和唯一性通常能够得到保证，但不能兼顾稳定性；2）如果约束太多，有可能使解不存在，这时就需要减少约束来保证存在性，但会造成解的数量明显增多，可以通过熵最大原则进行最优解的选择；3）上述所说的熵最大是从全局的角度考虑，而不是单独截取的某一段，具有最大熵的解能够满足唯一性。

2.2 MEM 求解不适定问题

为了更加深刻地理解最大熵法，下面以一维频谱为例，对其中涉及的3 种情况进行研究，见图2、图3、图4。

图2 时间域完整且无噪声

图3 时间域不完整但无噪声

图4 时间域不完整且有噪声

对于图2 的情况，时间序列（或时域数据）是完整且无噪声的，经过傅里叶变换后可以得到频域的唯一解。此类问题属于适定问题，不必应用最大熵法就可求解。

对于图3 的情况，时间域数据无噪声干扰，但是不完整，只获得了[-M,M] 的数据，由于未知区间数据的存在，导致变换后的频域解不唯一，一般情况下会产生无限多解。此类问题属于不适定问题，可以应用MEM 求解，即针对每一个解或未知数据外推计算其熵值，在结果中选定熵值最大的解或外推数据。这只是理想情况，实际工程中需要进行无限多次计算，因此这种方法不能应用。可以增加约束后进行求解，这里把数据作为约束进行求解。需要注意，时域中的最大熵和频域中的最大熵不是对应关系，因此产生了两种理论学派，即MEM1 和MEM2，这里不作详细阐述。

对于图4 的情况，时间域数据既有噪声干扰又不完整，在[-M,M]的噪声可能导致解不存在。当噪声强度较高时，即使可以对未知部分进行外推，傅里叶变换后的频谱也可能是负值，这与实际工程是不符的，所以这种情况解不存在。当噪声强度较低时，解虽然存在，但是根据第2 种情况，也会存在无限多个，唯一性不能保证。此类问题也属于不适定问题，可以应用MEM 求解。这种情况在求最大熵时可以不必要求所有数据点都存在约束条件，只需满足[-M,M]上的数据偏差保持在合理范围即可，这样就满足了解的存在性。

在谱分析过程中，应用最大熵法可以处理不适定问题，具有提高分辨率和降噪的作用，目前已经被应用在统计学的多个领域，加以研究后必然能成为冲击回波信号处理领域具有广泛应用前景的一种方法。MEM 的分辨率较高，是通过对已知数据以外的信号进行近似估计，假定未知信号与现有信号具有相同的统计特征，这与实际工程中的情况也相吻合，同时更适用于短信号的识别，目前被广泛应用。

3 现场试验

3.1 检测原理概况

分析冲击回波在混凝土内部的多次反射频率可以实现厚度及缺陷的识别，冲击回波在完整混凝土内部的传播见图5，冲击回波在缺陷混凝土内部的传播见图6。

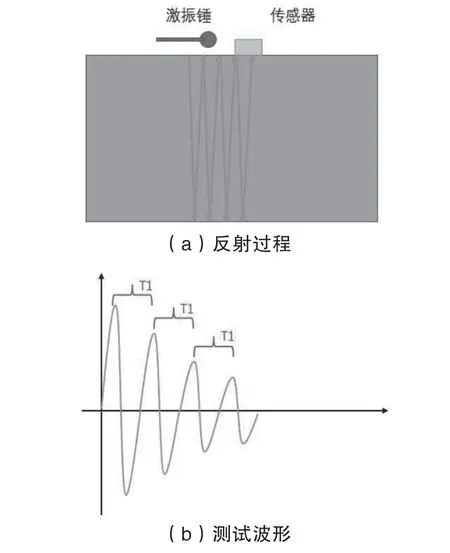
图5 冲击回波在完整混凝土内部的传播

图6 冲击回波在缺陷混凝土内部的传播

观察图5，发现冲击回波往返一次的时间为T1，即一个完整的传播周期，时频转换后的主频为1=1/T1，假设波速为VP，则测试厚度为H1=VP×T1/2=VP/(21)。观察图6，冲击回波遇到缺陷会发生提前反射和绕射，提前反射一次的时间为T2，绕射一次的时间为T3。则时频转换后的提前反射频率为2=1/T2，假设波速为VP，此时提前反射厚度即为缺陷深度H2，H2=VP×T2/2=VP/(22)。绕射后的反射频率为3=1/T3，此时测得的混凝土厚度H3=VP×T3/2=VP/(23)，由于绕射使传播距离增加、传播周期增大，导致计算频率降低，计算得到的厚度要比实际混凝土厚度大，称H3为名义厚度，存在关系H3>H1>H2，T3>T1>T2。

了解冲击回波的传播原理之后，就可以根据反射周期的提前和延后来判断缺陷的具体位置，见图7。图7 中缺陷位于底部正中，水平方向代表卓越周期（单位ms），竖直方向代表测点位置，测点从下到上等间距布置，从右侧图中可以看出：9-11号测点只存在一个明显峰值，说明此区域不存在缺陷，峰值位置即为结构实际厚度；7-8 号测点出现了两个峰值，第1 个不明显的峰值为冲击回波对缺陷的响应，说明测点已接近缺陷，第2 个峰值为结构厚度响应，厚度与之前相比无变化，说明测点没有正对缺陷上方，实际检测过程中需要重点观察附近测点；3-6 号测点出现两个明显峰值，第1 个峰值为缺陷深度的响应，说明测点已位于缺陷边缘，冲击回波能够完成绕射，第2 个峰值为厚度响应，发现厚度反射周期向后偏移，这主要是由冲击回波绕射导致，当出现此种情况时说明测点已经贯穿缺陷，可以进行标记；1-2 号测点只出现一个峰值且明显向后偏移，为厚度响应，说明测点已完全位于缺陷上方，且绕射频率占据主要地位。

图7 通过反射周期识别缺陷位置示意图

3.2 现场试验

试验选用仪器为冲击弹性波无损检测仪（简称PE），主要包括四个部分，如图8 所示。第1 部分为激振锤，用于冲击回波的激发，针对不同检测厚度可以选用不同直径型号。第2 部分为加速度传感器，通过数据线和主机相连，用于拾取冲击回波信号。第3 部分为PE 主机，分别连接电脑端和传感器，作用是将电压信号转换为数字信号，方便计算机进行数据记录，是整个测试流程的中转站。第四部分为便携式电脑端，内部装有PE 数据采集和分析软件，接收主机传来的数据并进行存储，采样完成后可对信号数据进行分析。

图8 试验仪器示意图

试验模型为混凝土材料，厚度0.3 m，尺寸为0.7 m×0.7 m×0.3 m，缺陷设置在正中底部，为了取得更好的测试效果，直接将底部0.1 m 厚位置挖空，尺寸为0.2 m×0.2 m×0.1 m，缺陷设置及测点布置见图9。每条轴布置26 个测点，测点间隔为2 cm，首个测点距模型边缘10 cm。（0.25,0.45），对比发现MEM 的计算结果更接近实际。这主要是由于FFT 算法进行谱估计时引入了数据窗，并没有对窗外数据进行合理的估计，所以造成数据泄露，但MEM 算法避免了这种情况，对窗外数据进行了合理估计，提高了分辨率和检测效果。

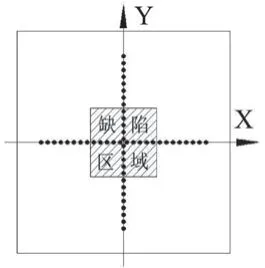
图9 缺陷设置及测点布置示意图

4 结果分析

应用FFT 和MEM 两种方法对采集的数据进行处理分析，通过对无缺陷的混凝土进行测试来标定波速，结果见图10，可知VP=3.809km/s，可用于后续混凝土缺陷的检测。X 轴和Y 轴方向的测试波形见图11，观察图11 发现波形图较复杂，无法直接从中获得关键信息，需要对其进行变换，下面从两个坐标轴方向分别对结果进行讨论。

图10 波速标定计算结果

图11 测试波形图

4.1 X 轴方向结果分析

将X 轴方向波形图应用FFT 和MEM 进行变换，得到的计算结果见图12。图12 中纵坐标代表测点位置编号，与图9 一致，FFT 计算结果中横坐标为频率（单位kHz），MEM 计算结果中横坐标为计算时长（单位ms）。观察图12（a），发现测点8-20位置的频率出现异常，根据频率计算公式，当缺陷出现时冲击回波的绕射会使频率降低，在FFT 计算图中表现为峰值频率提前。观察图12（b），发现测点8-17 位置的卓越周期出现异常，根据应力波的传播规律，缺陷处的绕射导致传播周期变长，在MEM 计算图中表现为峰值延后。

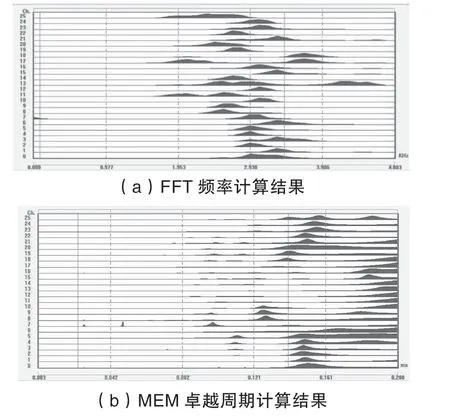
图12 X 轴方向变换结果

为了更加直观地识别缺陷，绘制了X 轴方向检测结果的等值线图，见图13。图13 中纵坐标为测点位置（单位m），FFT 计算结果中横坐标为频率（单位kHz），MEM 计算结果中横坐标为换算厚度（单位m），假设混凝土边缘坐标为0，彩色部分代表能量集中区。观察图13，等值线图可以更直观地标记出缺陷的位置，FFT 的计算结果为（0.30,0.47），MEM 的计算结果为（0.23,0.44），缺陷的实际位置为

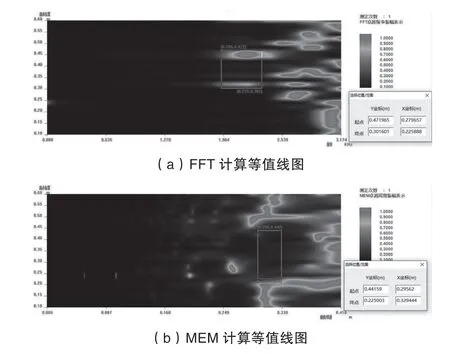
图13 X 轴方向等值线图

4.2 Y 轴方向结果分析

将Y 轴方向波形图应用FFT 和MEM 进行变换，得到的计算结果见图14。观察图14（a），发现测点6-18 位置的频率出现异常，频率提前。观察图14（b），发现测点8-17 位置的卓越周期出现异常，峰值延后。

图14 Y 轴方向变换结果

为了更加直观地识别缺陷，绘制了Y 轴方向检测结果的等值线图，见图15。观察图15，等值线图可以更直观地标记出缺陷的位置，FFT 的计算结果为（0.20,0.45），MEM 的计算结果为（0.24,0.47），缺陷的实际位置为（0.25,0.45），对比发现MEM 的计算结果更接近实际，分辨率更高，检测效果更好。

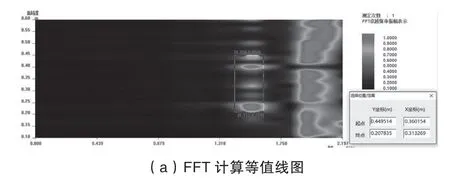
图15 Y 轴方向等值线图

5 结论

运用理论分析和模型试验研究了FFT 和MEM在冲击回波识别混凝土缺陷尺寸中的应用，总结了FFT 和MEM 理论的基本原理，对设置缺陷混凝土模型进行了检测，得出以下结论：1）FFT 算法简单快速，分析过程添加的窗函数会导致频谱泄露和分辨率降低；2）MEM 算法的分辨率较高，可以对已知频谱外的信号进行近似估计，更加适合实际工程检测，尤其对短信号的识别效果更佳；3）频谱图和卓越周期图中可以携带缺陷信息，缺陷在FFT计算结果中体现为峰值提前，在MEM 卓越周期计算结果中体现为峰值延后；4）等值线图可以更加直观地识别缺陷位置，MEM 的计算结果比FFT 计算结果精度更高，是识别混凝土缺陷尺寸的一种理想方法，具有广阔的应用前景。