基于热电效应高倍聚光焦面能流密度测量研究

张肖，刘霜，王亚辉，邱云峰，赫英贤

(1.华润电力投资有限公司沧州分公司，河北 沧州 061758;2.内蒙古工业大学 能源与动力工程学院，内蒙古 呼和浩特 010051;3.中国广核新能源控股有限公司内蒙古分公司，内蒙古 呼和浩特 010000）

0 引 言

为了提高太阳能利用效率，实现能量的梯级利用，太阳能聚光技术得到快速发展[1-3]。高倍聚光器将太阳光汇聚在焦面上，能流密度的分布情况是衡量聚光效果的重要参数，受到聚光器形状误差、反射表面粗糙度和跟踪系统精度等多重因素影响[4]。太阳能聚光热发电中，能量的高效利用取决于接收器最佳接收位置和采光口的能流密度分布[5-6]。因此，聚光焦面上能流密度分布对聚光效果评价和接收转换子系统优化具有重要的指导意义，是研究高倍太阳能聚光光伏发电或热发电系统多物理场耦合的基础。

Elsayed等[7]采用美国Alphatometer型能流密度传感器，对中心平板式聚光集热系统的焦面能流密度进行了测量，为保证传感器的精确定位，设计了软件控制系统，其传感器测试端采光口直径15.8mm，灵敏度为414.94 W/(m2·mV)。王富强等人[8-9]采用法国CapTec公司生产的HT50M20型水冷能流密度传感器对自行研制的多碟聚光器焦面能流密度进行了测量，传感器采光口直径为16mm。白凤武、王志峰等[10]发明了碟式聚光器聚光焦面能流密度测量装置，利用能流传感器分时测量有限点处能流密度值，结合插值算法，绘制出焦面上能流密度的分布情况。能流密度传感器要采用水冷降温，水冷腔造成采光窗口面积较大，而聚光器聚焦焦面面积有限，故直接测量方法传感器布置数量有限，采集精度低，后续数据处理分辨率差。为了进一步增加测试的分辨率和适用范围，研究者提出了间接测量方法。间接测量法是采用光学成像原理对能流密度分布进行测量，在聚光系统的焦平面处安置一个朗伯靶，朗伯靶各向同性反射汇聚来的太阳光束，在聚光系统侧用 CCD 相机拍摄朗伯靶表面上的能流密度场分布图。澳大利亚Johnston等[11-12]在研究White-Cliffs太阳能热电站中碟式聚光系统的焦面能流密度分布时采用了这种测量方法；国内的戴景民等[13-14]和肖君[15]采用该方法进行了高倍聚光器焦面能流密度分布的研究工作。间接测量要利用CCD相机对郎伯靶图像采集，图像灰度值与入射能流间的函数关系需要通过实验确定，缺乏通用性。

本文提出了一种基于热电效应的铠装热电偶间接测量法。当铠装热电偶在聚光器焦面上接受聚光光线照射时，会吸收入射光线能量，达到热平衡后，输出对应的温度值，入射光线能流密度和热电偶输出温度间存在着热力学关系。建立热电偶传热模型，分析其传热过程，得到传热函数，利用其反函数开展焦面能流密度测量。铠装热电偶测量端面直径较小（最小到3mm），可以多点布置，实时测量，精度高，速度快。本文对布置在高倍聚光焦面上的单支铠装热电偶传热模型开展研究，分析环境因素对模型的影响，并通过实验对传热模型进行验证，为后续多点测量传热模型的建立奠定基础。

1 传热模型

1.1 测量原理

选用WRNK―191型铠装热电偶作为研究对象，其实物和结构如图1所示。

图1 铠装热电偶实物及其结构

热电偶由探头、保护套管、电偶丝、MgO绝缘材料和密封胶五部分组成。探头材料为GH3039耐高温合金钢，电偶丝为镍铬―镍硅材料，保护套管为304不锈钢。MgO粉末保证电偶丝与探头之间绝缘，套管内密封胶为灌封黑胶。测量端是指热电偶丝的热端（镍铬电极与镍硅电极的接点处），热电偶输出温度为该点温度。探头处GH3039耐高温合金材料具有较强的抗氧化性和耐高温能力，长时间测量的极限温度为1100℃，短时间测量的极限温度为1300℃[16]。铠装热电偶探头端面直径为4mm，采光窗口小，在焦面上可多点布置提高测试分辨率。

基于热电效应的单支热电偶能流密度测量原理如图2所示（以碟式聚光器为例），热电偶垂直于聚光焦面放置，聚光光线照射在探头端面上，部分光线被端面反射到环境中，剩余部分被吸收，转换为热量传导到其内部和后部。在传热同时探头和套管表面温度不断升高，并通过对流和辐射方式对环境散热。当吸热和散热达到平衡后，铠装热电偶处于稳态传热过程，测量端输出温度的数值稳定，此温度值对应着固定的入射光线能流密度值。传热达到稳态时，热电偶能流如图3所示。

图2 测量原理简图

图3 稳态时铠装热电偶的能流图

通过测量与能流密度有关系的参数来反演得到能流密度值，该方法也是一种间接测量方法。技术关键在于构建铠装热电偶的传热模型，分析输出温度与入射能流密度间的函数关系，进而用其反函数和热电偶输出温度开展聚光焦面能流密度测量工作。

1.2 传热分析

从吸收聚光能流到温度稳定下来，铠装热电偶传热过程十分复杂，为简化模型，做如下假设：

1)铠装热电偶垂直于聚光器焦面布置，与聚光器采光口直径相比，热电偶探头端面直径小得多，故假设聚光后的光线垂直照射在热电偶探头上，不考虑入射角对端面反射率的影响；

2)各种材料间接触良好，且每种材料各向同性；

3)各接触热阻影响较小，在此忽略不计，认为接触良好。

铠装热电偶端面吸收的聚光太阳能能流E为：

式中：I为铠装热电偶接收的聚光太阳能能流密度，kW/m2；A为铠装热电偶端面面积，m2；D为端面直径，m。

少部分聚光太阳能能流被铠装热电偶的端面反射，反射的能流qref为：

式中：β为铠装热电偶表面的反射率。

大部分聚光太阳能能流被铠装热电偶端面吸收，吸收的能流qabs为：

式中：α为铠装热电偶表面的吸收率。

吸收的聚光太阳能能流qabs作为载荷施加在热电偶的端面上产生热传递；达到传热平衡后，流入铠装热电偶的能量（即qabs）等于流出铠装热电偶的能量（即图3中的辐射换热和对流换热）。由稳态导热的控制微分方程及附加的边界条件，该传热模型分析如下：

上式中，x为所在区域边界上的点，边界∂Ω、∂Ω1、∂Ω2分别指铠装热电偶本体、铠装热电偶施加载荷面、铠装热电偶的外表面；T、λ、qv分别是温度场分布函数、导热系数和内热源强度；q是边界∂Ω1上的给定的能流密度，即铠装热电偶端面上施加的载荷；h和Tb分别是边界（铠装热电偶的外表面）上的对流换热系数和环境温度；σ、ε、A分别是斯蒂芬-波尔兹曼常数(为5.67×10-8W/(m2·℃))、边界的辐射率和辐射面积。

该稳态传热为非线性传热，方程(3)至(6)采用数值方法（如有限元方法）进行离散求解时，可以转化为求解热平衡矩阵方程：

其中[K]为传导矩阵，包含导热系数、对流系数和辐射率；{T}为节点温度向量；{Q}为节点热流密度向量，包含热生成。

1.3 参数的设定

1.3.1 导热系数的确定

热电偶丝很细，忽略其对传热的影响，仅考虑其他材料的导热。MgO粉末导热系数随粉末的压实程度增大而增大，在此取17.3 W/(m2·℃)，密封胶为灌封导热黑胶，固化后导热系数为0.6W/(m2·℃)，探头和保护套管材料的导热系数随温度变化较大，其值如表1所示。

表1 两种材料的导热系数

1.3.2 对流换热系数的确定

对流换热系数受热电偶外表面温度、环境温度和空气流速等影响，由下式确定：

式中：h为对流换热系数；λ为已知条件下流体(空气)的导热系数；l为特征长度，这里指铠装热电偶的直径D。

努赛尔数Nu的确定分为以下几种情况：

1) 当Gr/Re2≤0.01时，自然对流的影响相对于强制对流可以忽略不计。此时，铠装热电偶竖壁面和水平壁面实验关联式的形式分别为：

竖直面：

水平面：

2) 当Gr/Re2≥10时，强制对流的影响相对于自然对流可以忽略不计。铠装热电偶竖壁面和水平壁面实验关联式的形式分别为：

竖直面：

水平面：

3) 当0.01≤Gr/Re2≤10时为混合对流，采用下式进行估算：

式中：Gr*=GrNu；NuM、NuF和NuN分别为混合对流时的Nu数、按强制对流和自然对流关联式计算的Nu数；系数C1、C2、C3和指数1、m、n、o为实验确定的常数，其取值参考文献[17]；各关联式的定性温度为tm=(tw+t∞)/2，其中tw为壁温，t∞为环境温度，特征长度为铠装热电偶外径D。

空气的各项参数取标准大气压下干空气的参数值，空气流速取2.6m/s，按上述方式计算铠装热电偶各部分的对流换热系数，计算结果如表2所示。

表2 铠装热电偶各部分的对流换热系数计算结果

1.3.3 反射率及发射率的确定

由基尔霍夫定律可知，物体的吸收率α与发射率ε相等。由于铠装热电偶表面的材料透过率为0，故其反射率β=1−α。

铠装热电偶表面的材料分为两部分，探头表面的材料为GH3039高温合金，套管表面材料为304不锈钢。物体表面的发射率取决于物质种类、表面温度和表面情况。铠装热电偶的表面经过抛光处理，其探头和套管表面的反射率随温度的变化如表3所示[18]。

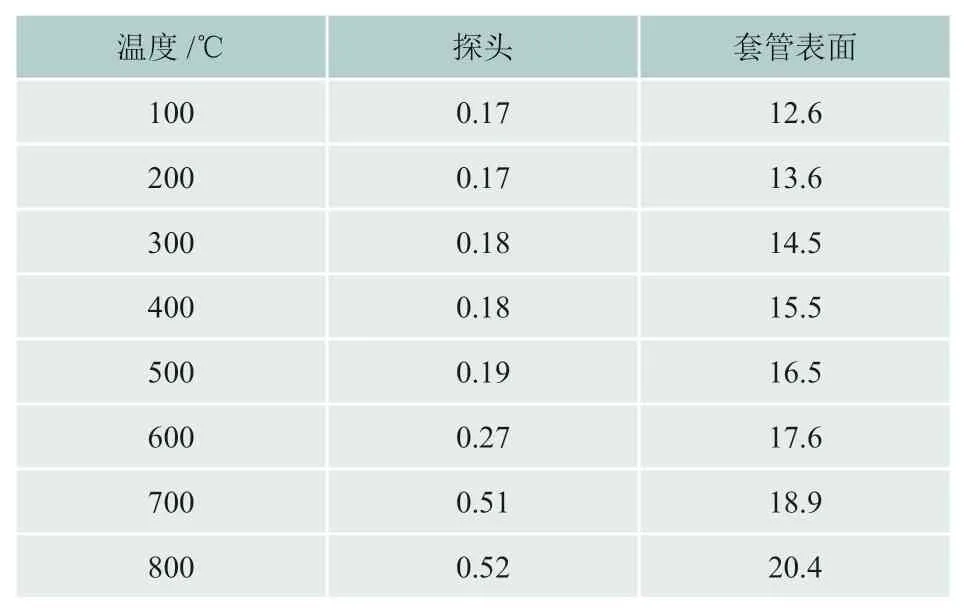
表3 铠装热电偶表面的吸收率

2 仿真分析

2.1 仿真结果

构建铠装热电偶的传热模型后，用ANSYS软件对其进行分析。环境风速和温度分别设定为2.6m/s、22℃，热电偶端面入射能流密度的范围从0到800kW/m2，将导热系数、对流换热系数和发射率等参数作为边界条件输入到软件中，计算铠装热电偶输出温度。热电偶输出温度与入射能流密度间的稳态传热模型结果如图4所示。

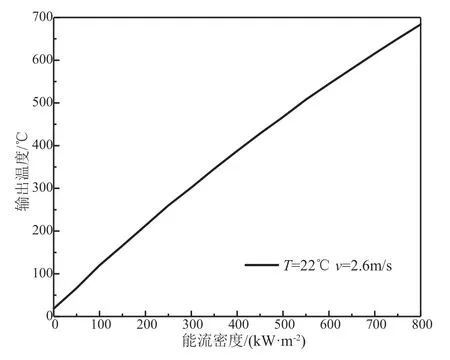
图4 铠装热电偶传热模型曲线

当端面吸收能流为0时，铠装热电偶的输出温度为环境温度22℃。随着能流密度的增大，铠装热电偶的输出温度随之增大，当能流密度达到800kW/m2时，输出温度达到683.76℃，但曲线的斜率随能流密度的增大而减小。端面吸收能流较小时，热电偶的散热以对流换热为主，辐射散热占比小，温度上升幅度大，曲线斜率大；随着端面吸收能流的增大，铠装热电偶外表面温度随之增大，对流换热占比减小，辐射散热占比增大；端面吸收能流较大时，铠装热电偶的散热以辐射散热为主，对流换热占比小，辐射散热量与温度的四次方成正比，输出温度上升幅度变小，曲线斜率变小。

回归分析得到铠装热电偶端面吸收能流和输出温度间的方程式为：

式中：I为入射能流密度，kW/m2；T为铠装热电偶输出温度，℃。

2.2 环境参数对传热模型的影响

铠装热电偶接收聚光能流照射后会迅速升至几百度高温，外部环境（风速、温度）的变化会带来较大影响。环境风速主要影响铠装热电偶的对流换热，在环境温度T=20℃的条件下，风速分别为1.4m/s、2.0m/s、2.6m/s、3.2 m/s、3.8 m/s、4.4m/s时传热模型仿真结果如图5所示。

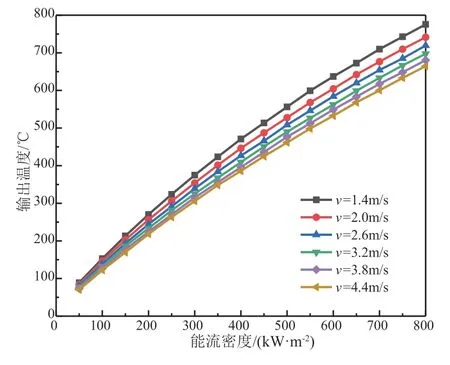
图5 环境风速对传热模型的影响

从图5可以看出，环境风速对传热模型影响较大。随着风速的增加，热电偶外表面与环境对流散热量增大，故端面吸收能流相等时，热电偶输出温度降低，随着能流密度的增加，这种差距愈发明显。当能流密度为800kW/m2时，1.4m/s风速和4.4m/s风速下对应的热电偶输出温度分别为775.66℃和664.53℃，两者相差高达111.13℃，因此在应用中要避免环境风速变化过大。

由各传热方程可知，环境温度对导热、对流和辐射都有影响。在环境风速v=2.6m/s的条件下，分别取环境温度为−20℃、−10℃、0℃、10℃、20℃、30℃进行传热分析。环境温度对传热模型的影响如图6所示。

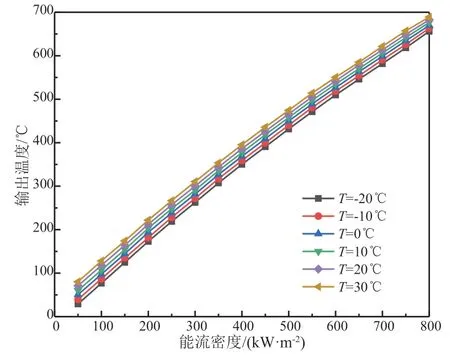
图6 环境温度对传热模型的影响

由图6可知，环境温度越高，传热模型曲线越平缓。随着能流密度的增大，曲线逐渐靠拢，环境温度对传热模型的影响逐渐减小。当端面吸收能流密度为800kW/m2、环境温度为−20℃和30℃时，铠装热电偶输出温度分别为656.32℃和688.9℃，两者相差为32.58℃，小于环境温度变化的差值（50℃）。环境温度对传热模型的影响较小，尤其是能流密度比较高的情况。

实际测量时，热电偶传热达到稳态所需时间较短，此过程中环境温度变化较小，对关系式的影响可以忽略。而环境风速有较大的不稳定性，尤其对于一些多风地区，环境风速变化过大会给测试带来较大的误差。因此，实际测量时需注意风速的变化。若风速变化较大，可以利用图5仿真结果进行修正。

3 验证实验

3.1 实验介绍

为便于操作，采用菲涅尔透镜搭建实验系统，开展实验研究，对传热模型开展验证。实验原理如图7所示，两块同样规格的菲涅尔透镜固定于同一平面上，将能流密度计和铠装热电偶的测量端分别固定在两块菲涅尔透镜的焦点处，同一平面上其能流密度相同，能流密度传感器输出能流密度数值，数据采集仪记录铠装热电偶输出温度。

图7 验证实验系统示意图

菲涅尔透镜的尺寸为15cm×15cm、焦距为18.2cm，能流密度计为EDTHERM公司Gardon64系列圆箔式热流传感器，并配有循环制冷机。台架置于跟踪平台上，对太阳进行实时全自动跟踪。菲涅尔透镜900倍的聚光倍数确保了足够大的测量上限，能流传感器和铠装热电偶可以上下移动，进而调节测量面上的能流密度大小。

3.2 结果分析

于2019年7月15日开展验证实验，测试时间为11∶50―13∶30，期间环境平均风速为2.5m/s，环境平均温度为31.98℃。

测试时，首先铠装热电偶测量端位于菲涅尔透镜焦面位置，然后调整铠装热电偶使其测量端下移1mm，测量范围最大离焦面9mm，共10个位置。每个位置调整时间为5min，保证热电偶达到传热平衡状态（热电偶的响应时间为30s）；测试时间为5min；接着调整测点下移1mm，如此循环，测量铠装热电偶输出温度和能流密度间关系。实验测得数值和模型仿真结果的对比，如图8所示。

图8 仿真曲线与实测数据对比

由于环境参数的变化、跟踪平台的跟踪误差、实验设备的装配误差以及测量过程的操作误差等因素的存在，使得实测数据与计算曲线有一定偏差。能流密度在0～400kW/m2时，实验相对误差为10%左右；随着能流密度的增大实测数据与仿真曲线越来越吻合，入射能流密度在400～600kW/m2之间，实验相对误差在8%以内；入射能流密度在600～800 kW/m2时实验相对误差在5%以内。

实验过程中，通过红外热像仪拍摄铠装热电偶外表面红外图像，利用SmartView软件分析图像，得到铠装热电偶径向温度分布曲线，将其与模型仿真数据对比，如图9所示。

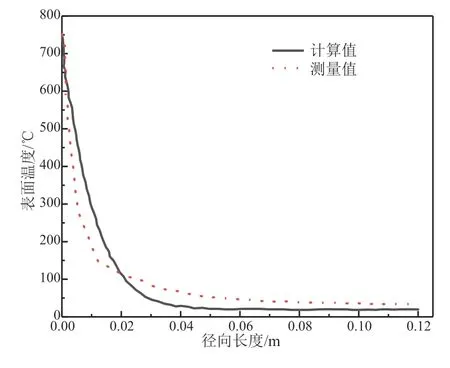
图9 铠装热电偶表面温度分布实测值与计算值对比（E=798KW/m2）

由图9可知，仿真和实测的铠装热电偶径向温度分布有着相近的分布规律。在离测量端0～0.01m的范围内，实测曲线的下降比计算曲线明显；在离测量面0.01～0.05m的范围内，计算值比实测值下降得更快；在离测量端0.05～0.12m的范围内，计算曲线和实测曲线都趋于平稳，温度变化很小，能流密度值越大，这种变化越小。

对比分析可以看出，铠装热电偶和能流传感器的输出数据与仿真曲线有较好的一致性，实测与计算得到的铠装热电偶表面温度分布也有近似的分布规律。由此证明，基于热电效应原理利用铠装热电偶测量能流密度的方法是可行的。

4 结论

提出了一种基于铠装热电偶测量能流密度的方法，建立了铠装热电偶的传热模型，计算得到能流密度与铠装热电偶测温值之间的热力学关系，并针对该函数关系做验证实验，得到以下结论：

1)通过数值分析，得到环境风速为2.6m/s、环境温度22℃时铠装热电偶入射能流密度与输出温度间的传热模型。

2)分析了环境参数对传热模型的影响，环境风速影响明显，环境温度影响较小。此结论为铠装热电偶能流密度测量装置的结构设计提供了依据，结构设计中最好屏蔽环境风速的影响。

3)开展验证实验，实测数据与仿真曲线吻合度较好，能流密度大于600kW/m2时，相对误差在5%以内；仿真和实测不同能流密度下铠装热电偶表面温度分布规律一致性较好，为实际测量提供了理论支持。