广播星历旋转误差对低轨星载BDS-3/GPS实时精密定轨影响分析

李 敏, 王煜斌, 李文文,2, 蒋科材, 陈 国, 赵齐乐

(1.武汉大学卫星导航定位技术研究中心,武汉 430079;2.香港理工大学土地测量与地理资讯学系, 香港)

0 引言

随着低轨卫星在大气掩星观测、地形形变监测及低轨导航增强等领域的应用,其对在轨轨道处理的精度和时效性要求越来越高;另外,低轨卫星的自主运行同样需要低延时甚至实时的卫星位置及速度信息[1-3]。星载GNSS (global navigation sate-llite system)技术具备观测精度高、全球覆盖广及成本低等优势,在低轨卫星的实时轨道确定方面得到了大量的研究和应用。

GNSS广播星历能够在不依赖地面的情况下实时更新,可充分满足星载GNSS实时定轨对实时性与自主性的要求,因此被广泛应用。广播星历误差是限制星载GNSS实时精密定轨精度的主要因素。通常采用空间信号测距误差(signal in space ranging error, SISRE)[4]来描述广播星历中的轨道和钟差误差的综合影响。Galileo卫星由于使用了具有高稳定度的原子钟且更新间隔仅10 min,其SISRE可达0.3 m 以内,是目前所有 GNSS 星座中精度最高的[4-5]。得益于国产高稳星载原子钟和星间链路技术的应用,北斗三号广播星历中地球轨道(medium Earth orbit, MEO)卫星轨道均方根(root mean square, RMS)误差和钟差标准差分别达到0.5 m和1.8 ns,其SISRE对应在 0.5 m水平,仅为北斗二代卫星的一半[6-9]。GPS的SISRE 在0.7 m 水平,分别是BDS-3和Galileo卫星的1.4倍和2.3倍。

为了提高实时定轨精度,Montenbruck等[10]最早提出将相位模糊度参数化为随机游走过程以吸收广播星历SISRE,Gunning等[11]则提出在实时定轨直接基于伪距和相位观测值估计GNSS星历SISRE。考虑到伪距观测的权重通常较小,这两种方法基本等价。GRACE和Swarm多颗低轨卫星在轨实测GPS数据的解算结果显示,该方法的三维定轨RMS误差能分别达到0.5 m和0.28 m水平[10,12-13]。基于该方法,国产资源三号、海洋二号卫星的实时定轨精度也从0.8～0.9 m提升至0.3～0.5 m量级[14-16]。另一方面,得益于更优的 SISRE 性能,利用 Galileo 和 BDS-3 可以显著提高实时定轨精度。以Sentinel-6A卫星为代表的星载Galileo实时定轨精度可以达到0.1m量级[17],而国产HY2D卫星基于BDS-3新频点信号B1C/B2a观测值也实现了0.2 m量级的实时定轨精度[18]。

然而,由于使用的地球定向参数(Earth orientation parameter, EOP)误差、动力学模型误差以及参与解算的地面站分布不均匀等因素,GNSS广播星历轨道存在着显著的星座整体平移、旋转和尺度误差。对于北斗系统广播星历,其尺度误差较小可以忽略,平移误差主要在Z方向并可以通过经验拟合较好地修正。广播星历旋转性误差主要是受到EOP误差的影响。北斗系统由于EOP更新较慢,其旋转误差最为突出,其RMS在X,Y,Z方向甚至达到2.0 mas量级[19]。广播星历整体旋转误差一方面影响GNSS轨道精度,通过改正旋转误差后BDS-3 倾斜地球同步轨道(inclined geostationary satellite orbit, IGSO)卫星的广播轨道RMS误差水平由0.7 m提升至 0.4～0.5 m,MEO由0.43 m提升至0.2 ～0.3 m[19-20];而另一方面,由于不同系统的星历旋转误差并不一致,多系统联合时旋转差异难以参数化吸收。利用BDS-3广播星历进行精密单点定位(precise point positioning, PPP)时,旋转性误差对定位结果的影响甚至达到10 cm[20-21]。

现有的基于星载GNSS的实时定轨并未充分顾及到广播星历中的整体旋转误差的影响。陆地探测一号(LUTAN-01)是中国资源卫星数据应用中心研制的L波段合成孔径雷达(synthetic aper-ture radar, SAR)卫星星座,用于监测地质环境、滑坡和地震灾害。LUTAN-01星座由两颗低轨卫星组成。其中,LUTAN-01A(LT-01A)卫星于2022年1月26日发射,其携带的GNSS 接收器和天线可以同时跟踪机载 GPS 和 BDS-3 信号。本文收集了2023年1月10日～2月4日期间LT-01A卫星的星载GPS与BDS-3观测数据,基于自主开发的星载GNSS实时定轨软件,分析广播星历旋转误差对基于BDS-3/GPS的低轨星载GNSS实时定轨的影响。

1 方法与数据

1.1 实时精密定轨模型方法

为了消除电离层延迟的影响,本文使用无电离层延迟组合观测值作为实时定轨的几何模型,如式(1)所示。

(1)

本文使用简化动力学方法进行低轨卫星实时定轨,该方法在动力学模型中添加经验加速度吸收卫星动力学模型误差,不易受动力学模型误差和几何测量误差的影响[22]。若星载GNSS观测值出现中断或质量过差,可利用轨道积分预报轨道,具有较高的稳定性[23]。为了更好地满足星载平台对计算效率、空间占用及数值稳健性等指标的要求,实时定轨软件采用平方根信息滤波(square root information filter, SRIF)[24]进行参数估计。低轨卫星动力学轨道通过轨道状态矢量表征。因此,滤波器中所有待估参数的状态矢量可表示为

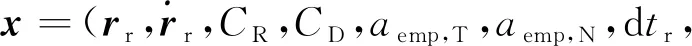
(2)

将上述无电离层组合观测值进行线性化,结合低轨卫星运动方程,构建滤波器的函数模型为

(3)

其中,i为历元;Φ为状态转移矩阵;W为过程噪声;z为观测值;A为观测值线性化的测量矩阵;v为测量噪声。

SRIF过程分为时间更新和测量更新。基于先验状态信息,通过数值积分预报当前历元低轨卫星的位置与速度及其方差信息,实现时间更新。利用预报的参数矢量线性化测量方程,再通过正交变换更新信息矩阵并转换为上三角阵,最后直接逆序求解参数完成测量更新过程[24-25]。

1.2 广播星历旋转误差提取及修正

广播星历旋转误差参数通过赫尔默特相似变换提取,以武汉大学解算的事后多系统精密轨道为参考,对广播星历轨道进行相似转换。具体的转换方程如下

rpre=rbrd+D+Rrbrd+Srbrd

(4)

根据上述方式提取GPS和BDS-3卫星旋转参数RX,RY,RZ。定轨计算时,式(1)中由广播星历计算得到的GNSS轨道按照式(5)改正整体星座旋转误差, 从而可分析广播星历旋转误差对低轨卫星实时定轨的影响。

(5)

1.3 数据

LT-01A卫星于2022年1月26日发射,位于高度600 km、倾角97.8°的近太阳同步轨道上。它携带一套 GNSS 接收器和天线,可以同时跟踪机载 GPS 和 BDS-3 信号。为了进行星上性能比较和相互备份,LT-01A卫星配备了两台独立双模GNSS接收机,能够同时跟踪GPS和BDS多频信号。星载接收机能跟踪所有 GPS 卫星的 L1 C/A、L2 P(Y) 频点信号和除北斗地球静止轨道卫星外所有 BDS-2 和 BDS-3 卫星的B1I、B3I 频点信号以及BDS-3卫星的B1C、B2a 频点信号。

收集了LT-01A卫星2023年1月10日～2月4日期间共25天的星载GPS和BDS-3观测值用于实时定轨分析,也对应收集了该时段内的GPS和BDS-3广播星历和精密星历用于分析广播星历旋转误差,从而验证其对LT-01A卫星的实时定轨精度的影响。

2 广播星历旋转误差

2.1 旋转误差参数

图1显示了所选择25天内的GPS和BDS-3广播星历与事后精密星历进行相似变换的三轴旋转参数序列。可见,GPS三轴旋转参数的变化幅度较小,基本上在±2 mas范围之内变化。然而,该时段内BDS-3广播星历的旋转误差呈现较大的变化幅度。年积日2023/12天RX,RY和RZ3个旋转参数都接近于0,表示该天旋转误差较小;自此开始,RX和RY均呈现显著线性下降趋势,RY下降趋势最为显著,在2023/24天幅度最大达到-8.7 mas,RX最大降至-3.6 mas;RZ则呈现先上升然后下降的趋势,在2023/20天达到最大值7.4 mas。直至年积日2023/27天,3个旋转参数均减小至0附近,并在之后又开始逐渐增大。

图1 BDS-3和GPS旋转参数序列

文献[20]显示了RX和RY旋转误差和广播星历所采用的EOP误差呈现线性相关性,具体地,RX和Y轴极移误差相关,而RY和X轴极移误差相关。由于EOP预报误差随时间增大,受此影响,广播星历旋转误差也随即增加。BDS-3系统进行EOP预报模型更新周期一般在7天左右[20,27]。结合所选时段内BDS-3广播星历旋转参数及EOP误差的变化趋势,可判断年积日2023/12～2023/27天内BDS-3应未更新EOP预报模型,导致其旋转误差呈现较大的变化幅度。由于GPS采用美国国家地理空间情报局(National Geospatial-Intelligence Agency, NGA)每天更新的EOP预报模型[26-27],其整体误差较小,因此旋转误差相比BDS-3小且变化较为稳定。

表1中对所选时段内GPS和BDS-3广播星历旋转参数的RMS误差进行了统计。GPS广播星历X、Y、Z3个方向旋转RMS误差分别为1.17,1.09,1.17 mas,BDS-3则分别为1.76,4.81,2.45 mas。整体而言,BDS-3的旋转误差是GPS的2.5倍左右。

表1 BDS-3和GPS旋转参数统计

2.2 对广播星历精度影响分析

为了进一步分析GPS和BDS-3各自的广播星历旋转误差造成的轨道精度损失,图2显示了GPS和BDS-3广播星历在旋转误差改正前后的误差统计时序,即按天统计所有卫星广播星历在切向、法向和径向上的RMS误差。旋转造成的轨道位置误差与轨道高度直接有关;1 mas的旋转误差会导致MEO上约12 cm的位置误差, IGSO由于轨道更高,其影响量级约在20 cm左右[20]。因此,图2中BDS-3 IGSO和MEO两类卫星分别统计。

图2 添加旋转改正前后的GPS与BDS-3卫星广播星历轨道误差

显然可见,GPS广播星历由于整体旋转误差较小在1 mas左右,其改正前后轨道精度基本上没有变化,其切向、法向和径向轨道误差基本上分别在40,20,10 cm量级变化。BDS-3卫星则呈现显著的与旋转误差趋势和量级相对应的轨道误差。在年积日2023/20天BDS-3星历Z轴旋转误差达到最大,对应的BDS-3 IGSO和MEO在该天法向的误差达到最大,分别为54.1 cm和42.1 cm;而在2023/24天Y轴旋转误差达到最大为-8.7 mas,该天BDS-3 IGSO和MEO的切向误差分别为63.8 cm和43.2 cm,也是所选时段内最差的。BDS-3卫星广播轨道经过旋转修正后改进明显。整体而言,年积日2023/12～2023/27天在未修正旋转误差时,BDS-3 MEO卫星切向和法向误差保持在较高的水平,达到30 cm左右;进行旋转改正后,均降低至10 cm量级。对于BDS-3 IGSO卫星,其改进效果更大,切向和法向可以从40～60 cm改进至10～20 cm水平,最大降幅甚至超过50 cm。另一方面,由于旋转并不会改变位置矢量的长度,BDS-3 MEO和IGSO的径向误差并不受到旋转误差的影响,均在5 cm水平,比GPS高约1倍。

表2则对GPS、BDS-3 IGSO和MEO三类卫星在旋转改正前后的轨道误差进行统计。GPS整体改进不到1 cm,其切向、法向和径向误差平均为42.2,24.7和8.9 cm。BDS-3两类卫星均显示出显著改进。BDS-3 IGSO卫星的切向误差从31.5 cm降低至11.3 cm,法向从28.0 cm降低至12.9 cm,降幅分别达到64.0%和53.8%。BDS-MEO卫星切向和法向则分别从25.0 cm和20.0 cm降低至11.9 cm和8.7 cm,降幅分别为52.4%和57.1%。径向误差为导航系统空间信号精度的最主要的贡献分量,BDS-3 IGSO和MEO径向误差分别为6.3 cm和4.2 cm,比GPS分别小29.7%和53.3%。

表2 添加旋转改正的GPS和BDS-3广播星历轨道误差RMS统计值

3 LT-01A实时定轨

3.1 定轨策略

本文采用简化动力学方法进行实时定轨,实时定轨策略如表3所示,主要包括卫星动力学模型、观测模型及参数估计模型三大类信息。动力学模型方面,由于低轨星载平台算力有限、内存资源紧张,实时定轨的动力学模型相对于事后精密定轨需要进行简化,重力场模型仅采用静态场,海潮摄动仅为5×5 阶次。根据已有的星体几何模型信息构建了简易的Box-wing模型以计算大气阻力、太阳辐射光压等非保守摄动力;由于星体受照面和迎风面计算需顾及姿态,本文采用星载星敏传感器提供的姿态四元数数据计算LT-01A卫星姿态。本文采用简化动力学方法进行实时定轨,因此在切向和法向添加经验加速度补偿动力学模型中的误差。

表3 LT-01A实时定轨策略

实时定轨的观测模型如式(1)所示,采用基于BDS-3 B1C/B2a及GPS L1/L2的双频无电离层组合观测值,定轨弧段为2023年1月10日～2月4日。参数估计方面,实时定轨采用SRIF作为参数估计器,待估状态量如式(2)所示。其中,大气阻力系数、太阳光压系数、接收机钟差、广播星历误差吸收参数及切向/法向经验加速度作为随机游走参数估计,模糊度参数作为常量估计。

3.2 定轨结果

根据上述方法,本文采用自主开发的星载GNSS实时定轨软件对2023年1月10日～2月4日的LT-01A星载GPS与BDS-3观测值进行模拟星载实时定轨处理,包括基于GPS、BDS-3及GPS/BDS-3观测值的实时定轨。为了分析广播星历旋转误差对实时定轨精度的影响,所有实时定轨处理均包括不考虑旋转改正和添加旋转改正等两组处理结果。为评估实时定轨精度,采用武汉大学事后精密轨道钟差产品计算了LT-01A精密轨道,其6 h重叠弧段精度优于1 cm,具有较好的轨道一致性,可以作为参考值。

图3显示了基于星载GPS、BDS-3、GPS/BDS-3观测值的实时定轨在旋转误差改正前后的切向、法向和径向定轨误差单日RMS统计时序。由于GPS广播星历整体旋转误差较小且旋转改正前后的广播星历轨道精度基本不变,基于GPS的实时定轨精度在添加旋转改正前后基本没有变化,其切向、法向及径向误差分别在 20～40,10～20和10～15 cm内变化。

图3 LT-01A卫星实时定轨误差单日统计(黑色:旋转改正前;红色:旋转改正后)

基于BDS-3的实时定轨则显著表现出与旋转误差趋势对应的定轨误差变化。在年积日2023/18～27 天BDS-3广播星历Y轴与Z轴旋转误差增大时,实时定轨的切向与法向误差也出现了明显增大的趋势。当年积日2023/20天BDS-3广播星历Z轴旋转误差及广播星历轨道法向误差达到最大时,实时定轨的法向误差最大,为24.0 cm。当年积日2023/26天BDS-3广播星历轨道切向误差最大时,基于BDS-3的实时定轨切向误差也达到最大,为31.1 cm。添加旋转改正后,基于BDS-3的实时定轨误差在旋转误差较大的年积日2023/18～27时段内显著降低,切向定轨误差从30 cm量级降至20 cm量级,法向定轨误差从 20 cm量级降低至 15 cm以下。其中,年积日2023/23天时切向定轨误差改善最大,为13.8 cm;年积日2023/20天时法向定轨误差改善最大,为11.6 cm。由于卫星轨道径向基本不受旋转误差的影响,基于BDS-3的实时定轨径向误差基本不受旋转改正的影响。

基于GPS/BDS-3联合观测值的实时定轨误差与基于BDS-3的实时定轨误差量级与变化趋势基本一致,该现象与文献[16]中基于星载GPS/Galileo的Sentinel-6A实时定轨结果类似。显然,旋转改正也显著提升了旋转误差较大时段的联合实时定轨切向与法向精度,切向精度提升最高为13.9 cm,法向精度提升最高为11.2 cm。添加旋转改正后的基于BDS-3的实时定轨与基于GPS/BDS-3的实时定轨的切向误差为20 cm量级,而基于GPS的实时定轨的切向误差仅为30 cm量级,比前二者差约33%。

表4统计了整个定轨弧段内的基于GPS、BDS-3、GPS/BDS-3的实时定轨在旋转改正前后的切向、法向、径向的误差RMS统计。由于GPS星历在旋转改正前后差别不超过1 cm,因此基于GPS的实时定轨基本不受广播星历旋转误差的影响。基于BDS-3的实时定轨精度在旋转改正后明显改善,切向误差由 24.7 cm降至21.0 cm,法向误差由15.7 cm降至10.7 cm,三维误差由31.9 cm降至26.7 cm,降幅分别为15.0%,31.8%及16.3%。基于GPS/BDS-3的实时定轨也显示出明显改进,切向、法向、径向和三维误差在改正前精度分别为22.4,14.5,11.3,和29.2 cm,改正后分别为19.4,10.7,11.2和25.0 cm,在切向、法向、三维分别提升了13.4%,26.2%及14.4%。得益于BDS-3广播星历较低的SISRE,单BDS-3定轨、GPS/BDS-3联合定轨的精度均优于单GPS定轨,未改正旋转误差时前二者总体定轨精度比后者分别高3.2 cm和5.9 cm,改善幅度分别为9.1%和16.8%,改正后则定轨精度提升更为显著,分别达到7.8 cm和9.5 cm,改善幅度达到22.6%和27.5%。由于冗余观测更多,联合定轨相比单BDS-3的实时定轨三维精度在旋转改正前后也分别提升了2.7 cm和1.7 cm,分别改善8.5%和6.4%。

表4 LT-01A定轨精度统计

4 结论

本文通过研究,得到如下结论:

1)BDS-3广播星历的X,Y,Z三轴旋转误差分别为1.76,4.81,2.45 mas,GPS广播星历的三轴旋转误差仅为1.17,1.09,1.17 mas。BDS-3广播星历的旋转误差约为GPS广播星历的2.5倍。

2)GPS广播星历轨道精度基本不受广播星历旋转误差的影响,而BDS-3广播星历轨道精度受广播星历旋转误差影响显著,且与卫星轨道高度直接相关。添加旋转改正后, BDS-3 IGSO卫星广播星历的轨道误差在切向、法向、径向分别为11.3 cm,12.9 cm,6.3 cm,相比于旋转改正前切向与法向误差降低了64.0%和53.8%。BDS-3 MEO卫星广播星历的轨道误差在切向与法向也降低了52.4%和57.1%,表明旋转改正可以有效消除旋转误差带来的BDS-3广播星历轨道精度损失。

3)由于GPS广播星历旋转误差量级较小,基于星载GPS的LT-01A卫星实时定轨精度基本不受旋转误差影响,其切向、法向、径向和三维定轨误差分别为29.2,13.2,12.3及34.5 cm。基于星载BDS-3以及BDS-3/GPS联合的实时定轨精度受BDS-3星历旋转误差影响严重,且主要作用于切向和法向。考虑旋转改正后,单独BDS-3实时定轨在切向、法向、径向RMS分别为21.0 cm,10.7 cm及11.2cm,其切向和法向精度比改正前分别提升15.0%和31.8%,总体三维精度则由31.9cm提高到26.7cm,改善幅度达16.3%;GPS/BDS-3联合定轨在切向、法向、径向精度分别为19.4 cm,10.7 cm和11.2 cm,切向和法向精度比未旋转改正时分别提升13.4%和26.2%,总体三维精度则由29.2 cm提高到25.0 cm,改善幅度为14.4%。得益于BDS-3广播星历较高的精度,单BDS-3以及BDS-3/GPS联合的实时定轨精度均优于单GPS定轨,未顾及星历旋转改正时前两者定轨精度比后者分别高9.1%和16.8%,添加旋转改正后精度提升幅度更加显著,分别达到22.6%和27.5%。

本文基于LT-01A的星载实测BDS-3/GPS数据验证了星历旋转误差对于低轨实时精密定轨的影响。由于旋转参数需通过广播星历与事后精密星历进行相似变换获取,后续将继续研究在实时定轨实施过程中同步估计星历旋转误差以满足实时在轨处理要求。