一种结合角距特征的改进栅格星图识别算法

徐俣长,张 扬,叶志龙,谢凤英,臧云朝,杨 光,袁 洪

(1. 中国科学院空天信息创新研究院,北京 100094;2. 中国科学院大学电子电气与通信工程学院,北京 100094;3. 上海交通大学电子信息与电气工程学院,上海 200240;4. 上海航天控制技术研究所,上海 201109;5. 北京航空航天大学宇航学院,北京 100191;6. 哈尔滨工业大学空间光学工程研究中心,哈尔滨 150001)

0 引言

天文导航是一种自主性强、隐蔽性高、不易受外界干扰且可以提供高精度姿态信息的自主导航方式[1],广泛应用于卫星、飞机及导弹等飞行器,同时也是深空探测领域中一种有效的自主导航方案[2]。星图识别是天文导航中的关键技术之一[3],主要完成对观测星图中的星点提取及识别,根据星图识别确定的星图坐标及其对应导航星的天文坐标即可得到星敏感器的姿态,因此星图识别成功率及准确率将直接影响飞行器导航定位及姿态确定性能。由于星图识别算法在天文导航应用中发挥着重要作用,因此得到了学者的广泛研究。

目前针对星图识别的研究主要集中在子图同构和模式识别两类算法及其改进方面。子图同构类算法是在观测星图中选定多颗恒星星点,基于星点几何分布构造匹配特征,并在导航星库中进行特征匹配实现星图识别[4]。子图同构类算法中三角形算法[5]最具代表性,该算法的优点是可靠性高、工程应用广泛[6],但算法识别特征维度低、计算冗余度高,且识别成功率易受噪声影响。模式识别类算法是分别构造观测星和导航星的模式向量,并根据两者的模式向量匹配结果完成星图识别。栅格算法[7]是一种典型的模式识别类算法,通过对星图划分栅格,根据栅格中是否存在星点构建特征模式,应用模式识别进行导航星匹配。栅格算法相较于三角形算法等子图同构类算法具有存储空间需求小,运行速度快等优势,但易受邻域星点分布的影响导致识别率下降甚至误匹配[8],且主要适用于大视场星敏感器中的星图识别。近年来对于栅格算法的改进研究不断深入,钱华明等[9]提出了一种扩充栅格算法并将算法的应用推广至观测星点数目少的小视场星敏感器中;为了提高星图识别的准确性,钱华明等[10]提出了通过构建特征模式的度量函数来反映栅格算法特征模式的内在相似程度,从而减小位置误差对星图识别的影响;李立宏等[11]针对栅格算法应用时观测星需求大的问题,提出了主星的概念并减少冗余模式,提高了算法的鲁棒性和实时性。

本文聚焦于大视场星图识别中栅格算法对近邻星依赖性较强、易受邻域星点分布影响等问题,提出了在栅格算法的基础上引入星角距特征对受近邻星影响的观测星进行再识别的改进方法,进一步提升算法的星图识别率,并且由于结合了栅格算法的高效性和角距特征的可靠性,改进算法具有更佳的综合性能。

1 改进栅格算法原理

改进栅格算法是一种在原栅格算法的基础上,通过设计和应用星角距识别模式对栅格识别模式的失效场景进行再识别的方法。

1.1 栅格模式构建流程

栅格算法是通过对星图划分栅格来构造主星唯一的模式向量以实现星点的匹配识别,其实现流程包括参考基准统一、栅格模式构建、栅格模式匹配三部分内容。

1.1.1 参考基准统一

由于导航星和观测星所处的坐标基准不同,在使用栅格算法时首先需要进行参考基准统一,先通过坐标转换和投影及平移变换将导航星位置矢量由天球坐标系(记为i系)转换到星敏感器成像平面坐标系(记为p系)。天球坐标系到星敏感器坐标系(记为s系)的姿态转换矩阵Tsi如式(1)所示

(1)

其中,(α0,δ0)为选定作为星敏感器视轴指向的导航星赤经、赤纬,且设定滚转角为0°。星敏感器坐标系s系到p系的投影和平移变换如式(2)所示

(2)

式中,(xp,yp)表示p系下的星点坐标;f表示焦距;a表示像元大小;(Xs,Ys,Zs)表示s系下的星点坐标;(x0,y0)表示星敏感器成像平面中心点的位置;m×n表示星敏感器成像平面的分辨率。通过计算式(1)和式(2),即可得到由i系转换到p系下的导航星的坐标。

1.1.2 栅格模式构建

在将导航星和观测星位置矢量统一到p系后,即可进行观测星和导航星栅格模式的构建,具体构建流程如下:

1)以模式构建对象为主星,确定主星模式半径pr(pattern radius)范围内的邻域星点;

2)将主星及其邻域星点进行平移,移至主星位于视场中心,根据缓冲半径br(buffer radius)确定近邻星;

3) 以主星为中心,主星和近邻星连线作为坐标轴旋转星图,至该坐标轴与x轴重合;

4)在星图中划分g×g栅格,栅格中若存在邻域星点则记cell(i,j)=1,反之则记cell(i,j)=0,根据g2个栅格的标记构造主星的特征模式向量p,具体表示为p=[c1,c2,…,ck,…,cg2-1,cg2],其中ck可由式(3)得到

(3)

其中,(i,j)表示栅格位置坐标,i∈[1,g],j∈[1,g];ck表示向量p的第k个元素值;k与i,j的关系式为k=(i-1)×g+j。整个构建过程如图1所示。

(a) 确定主星邻域星点范围

1.1.3 栅格模式匹配

在分别构建导航星和观测星模式向量后,即可计算导航星与观测星的模式匹配结果,如式(4)所示

(4)

其中,pi表示观测星模式向量;pj表示导航星模式向量;M(pi,pj)表示一对观测星与导航星模式匹配结果。最终匹配结果是找到各观测星与导航星特征模式向量按位求与所得结果的最大值,即确定与观测星模式最接近的导航星结果。以观测星1为例,其最佳匹配导航星计算过程如式(5)所示

M(p1,pm)=max(M(p1,pj)),j=1,2,…,n

(5)

式中,m表示与观测星1最佳匹配的导航星下标;n表示导航星数目总数。

1.2 栅格算法性能影响因素及失效场景分析

由1.1节可知,影响栅格算法性能的关键参数包括:栅格数目g、模式半径pr以及缓冲半径br。栅格数目g过小,则易出现多颗恒星位于同一栅格之中,导致模式特征数量减少;当栅格数目g过大,则无效模式特征维数增加,从而增加额外的运算时间。模式半径pr决定了恒星邻域的范围,一般为了增加邻域星点的数目,选取1～2倍星敏感器视场半径作为pr的值[10-11]。缓冲半径br主要用来确定近邻星的位置,由于观测星图中存在噪声星点,因此易导致观测星图和导航星图中的近邻星选择不一致,则两图旋转后的星图不一致,从而造成匹配失败。

基于上述分析,栅格算法失效主要包括以下三种情况:一是位于星图边界的星点,这些观测星的邻域星点数目较少,因此可能由于特征维数小而导致误匹配;二是近邻星选择错误,则导致旋转后的模式结果与匹配导航星模式结果不一致使得该星对无法匹配;三是由于栅格划分不当使得多颗邻域星点位于同一栅格,从而导致特征向量维数低,与匹配导航星模式不匹配。栅格算法各影响因素与其失效场景的对应关系图如图2所示。

图2 栅格算法影响因素与其失效场景的对应关系图

上述三种栅格算法失效的情况在模式识别过程中的表现为在遍历导航星库后,观测星的最大特征匹配值相较于正常观测星的匹配值低。从栅格算法原理可知,观测星的特征模式图一般是对应匹配导航星特征模式图的子图,一颗观测星的理论最大匹配值应与其邻域星点数目一致。考虑到实际情况中可能存在缺失星、伪星等影响匹配星点数目的因素,因此本文将观测星邻域星点数目的1/2作为临界条件,当观测星的最大特征匹配值大于临界值则说明匹配成功,反之则认为是上述三种匹配失效的情况,需再进一步识别。角距特征按照几何原理进行匹配,不易受邻域星点分布、近邻星位置以及特征维数的影响,因此将角距特征引入再识别过程,可以有效解决上述三种引起栅格算法失效的问题,接下来介绍星角距模式的特征向量构建。

1.3 星角距模式特征向量构建

星角距模式是以角距为分量的星点特征模式,其构建过程如图3所示。首先以主星为中心,以模式半径pr为半径确定主星的邻域星点;然后依次将主星和邻域星点组成星对,计算星对角距值记为d,并依次记录整理成一维向量v=[d1,d2,…,dn],其中n表示邻域星点数目;最后对向量v的元素进行排序得到主星的星角距模式,其模式特征向量的表达式pi为

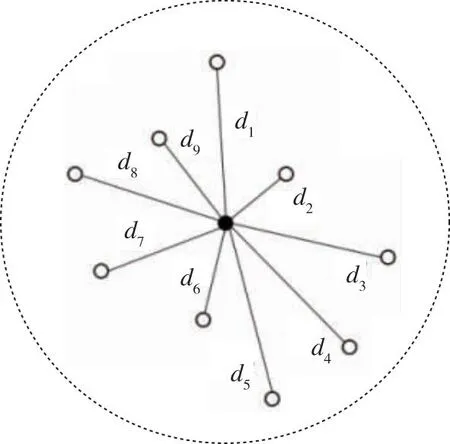
图3 星角距模式特征向量构建图

pi=[di1,di2,…,din]

(6)

其中,din表示第i颗主星与第n个邻星之间的角距。

角距匹配条件如式(7)所示,其中ε表示角距阈值,符合式(7)则认为观测星角距与导航星角距匹配。星角距模式匹配过程则是对星角距模式向量中的匹配角距元素计数,取与观测星元素匹配数目最多的导航星作为匹配导航星。

(7)

(8)

其中,si和sj为导航星在天球坐标系下的位置矢量,计算公式为

(9)

其中,(α,δ)为导航星的赤经、赤纬。

观测星星对角距计算公式为

(10)

其中,cm和cn为观测星在星敏感器成像坐标系下的方向矢量,计算公式为

(11)

在1.2节栅格算法性能下降的场景下,引入星角距模式对判定为栅格算法失效的观测星遍历匹配。在栅格算法的基础上进行角距匹配,可以大量减少待匹配观测星即减少比较匹配过程,在不显著增加时间消耗的同时提高了算法的识别率,同时可以提高算法的可靠性。

2 改进栅格算法的流程

改进的栅格算法以传统栅格算法为基础,通过对栅格算法失效场景引入星角距模式进行再识别来提高算法的识别率,算法流程如图4所示。在栅格模式下的星点匹配过程中,遍历比较各导航星的模式匹配值找到观测星的最佳匹配结果,若栅格模式下最佳匹配结果的最大特征匹配值大于观测星邻域星点数目的一半则视为匹配成功,反之则进入星角距模式进行再识别。在星角距模式下的星点匹配过程中,先将角距模式向量中的角距进行排序,再查找匹配角距,具体过程为将导航星和观测星的模式向量中的角距作差,若其差值小于角距阈值则认为角距匹配成功,最后选择匹配角距数目最多的导航星作为匹配结果。改进栅格算法的结果由两部分组成:对于有效的栅格算法保留其匹配结果,对于判断为失效的栅格模式下的观测星将进行角距模式再识别,记录角距模式下的结果,两者共同组成观测星图的星点匹配结果。

图4 改进栅格算法流程图

改进的栅格算法综合了栅格算法的快速性和角距类算法的稳定性,同时又规避了由栅格数目、近邻星选择不当等引起栅格算法误识别的问题,提高了算法的识别率。

3 算法试验及性能分析

3.1 试验设计

为了系统评估本文改进栅格算法的性能,分别设计了改进栅格算法识别效果测试试验、算法性能对比测试试验和算法环境适应性测试试验。其中改进栅格算法的识别效果测试主要是通过开展传统栅格算法和改进栅格算法的星图识别试验并对识别结果进行对比分析,以检验改进栅格算法的有效性和相较于栅格算法的识别能力的提升效果;改进栅格算法性能对比测试是从识别效率、存储容量和识别率等性能指标出发,进行改进栅格算法与三角形算法[5]、径向模式算法[12]、改进的对数极坐标变换(log-polar transformation, LPT)算法[13]以及星辐射模式匹配识别算法[14]等的星图识别试验和性能对比分析;算法环境适应性测试是通过在测试星图中考虑位置噪声、缺失星和伪星等干扰因素,从识别率的角度分析改进栅格算法的环境适应性及算法鲁棒性。

试验测试星图采用不同视轴指向下的仿真星图,其中星图仿真参数设置信息如表1所示,星表选择第谷2导航星表(Tycho-2)提供的导航星信息。

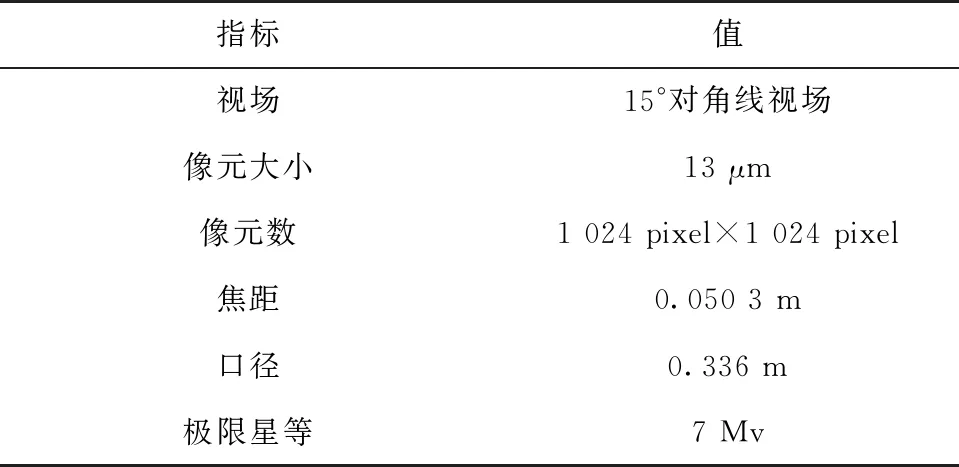
表1 仿真星图基本信息

改进前后栅格算法参数设置如表2所示。

表2 仿真试验中算法参数设计

3.2 试验结果分析

3.2.1 改进栅格算法识别效果分析

随机选取同一张仿真星图,分别应用传统栅格算法和改进的栅格算法进行星图识别处理。使用传统栅格方法得到的邻域星点分析结果如图5所示。其中图5(a)表示以观测星邻域星点数目的一半作为判断阈值时输出的匹配成功的星点数目,由图可知该条件可以有效地将栅格算法是否失效的观测星区分开,证明了阈值设置的合理性。图5(b)表示各观测星的邻域星点数目和使用栅格算法得到的最大匹配值的对应关系,图中点状标记表示匹配失败的星点,表明栅格算法失效的观测星点多为最大匹配值较小且与邻域星点数目差异较大的观测星点。

(a) 判断条件与匹配结果关系图

改进前后的栅格算法星图匹配结果如图6所示。图6(a)为传统栅格算法的匹配结果,图6(b)为改进栅格算法的匹配结果,其中红色星点表示正确识别结果,白色星点则表示误匹配结果。由图可知,由于边界星点在构造栅格模式时邻域星点分布集中在一侧,易导致匹配失败,而这些星点经过改进算法中的角距匹配后,在图6(b)中可全部得到正确匹配。表明采用本文改进的栅格算法有利于边界星点的识别,增加了星图中星点正确识别的数目、扩大了星点正确识别的星图范围。

3.2.2 算法性能测试结果对比

在不考虑环境干扰的情况下,基于仿真星图进行改进栅格算法与三角形算法等5种典型星图识别算法性能对比试验。其中测试环境为:硬件平台性能为(CPU:Intel(R) Core(TM) i5-9300H,8 GB),软件平台为MATLAB 2018。识别时间、空间占用及识别率统计结果如表3所示。对比表中的算法识别率可知,本文提出的改进的栅格算法的识别率可达98.88%,优于其他几种典型星图识别算法,其中高出原栅格算法7.87%;在识别效率和存储消耗方面,改进栅格算法由于增加了角距模式构建和角距识别环节,识别时间和空间占用均稍高于原栅格算法,但显著低于三角形算法。

表3 不同星图识别算法性能对比

3.2.3 算法环境适应性试验结果分析

在仿真星图的星点上叠加方差为0～0.5像素的位置偏差来模拟位置噪声,开展考虑位置噪声干扰下的算法识别率性能测试,识别结果如图7所示。由图可知,在不同位置噪声的干扰下,改进后的栅格算法识别率保持在95%以上,均显著高于原栅格算法,且随着位置噪声的增加,改进后的栅格算法相较于角距类算法星图识别率变化幅度更小,说明改进栅格算法抗位置噪声影响能力更强,鲁棒性更佳。

图7 位置噪声影响下的星图识别率

不仅如此,由于星点的位置误差直接影响着角距的结果,因此三角形算法等角距类星图识别算法识别率波动较大,但如栅格算法等模式识别类算法由于是根据一定角距区间内是否存在星点而构建模式特征进行识别,识别率受位置噪声影响较小。本文改进的栅格算法具有栅格算法的优势,在位置噪声影响下具有较好的性能结果,并且还通过角距二次识别提高了算法的识别率。

在仿真星图中随机去除1～5个已成功提取出的星点,来模拟缺失星存在的情况,开展考虑缺失星干扰下的算法识别率性能测试,识别率结果如图8 所示。由图可知,改进的栅格算法在存在不同数目的缺失星条件下识别率变化趋势平缓,下降率较低,在1～5个缺失星下识别率均可达到95%以上,相较于原始栅格算法及其他算法性能较优。

图8 缺失星影响下的星图识别率

此外,整体而言,相较于栅格算法,角距类算法受缺失星影响较小。主要是由于缺失星使得栅格算法的模式特征维数下降,导致误匹配增加,识别率会随着缺失星数量的增加而显著下降。本文改进的栅格算法由于加入了星角距识别模式,可以充分利用角距类算法的优势对受缺失星影响而匹配失败的星点进行再匹配,因此算法的鲁棒性和识别率均处于较高水平。

在仿真星图中随机添加1～5个不存在的星点,来模拟伪星干扰场景下的星图结果,开展考虑伪星干扰下的算法识别率性能测试,算法识别结果如图9所示。由图可知,改进的栅格算法在伪星干扰下识别率始终高于原栅格算法和三角形算法,但识别率受伪星数目增加的影响较大。主要是由于改进的栅格算法结合了角距类算法和栅格算法的特点,其中伪星会影响角距特征向量构建从而影响星点的识别,同时会使得栅格模式向量中不匹配星对的匹配维数增加从而引起误匹配。因此改进栅格算法的识别率虽优于三角形算法和原栅格算法,但伪星仍然对算法识别率有一定的影响,且在稳定性方面略低于径向模式算法。对于这一问题,在实际应用改进栅格算法时,可以在星点提取环节中采用多帧对比的方法滤除伪星点[15],以减小伪星对星图识别算法识别率的影响。

图9 伪星影响下的星图识别率

4 结论

本文提出的结合角距特征的改进栅格算法,通过引入星角距模式对栅格算法误匹配的观测星进行再识别,解决了栅格算法识别率易受观测星邻域星点影响的问题,主要结论如下:

1)改进的栅格算法识别率可达98.88%,相较于传统栅格算法的识别率提升了7.87%;

2)在考虑位置噪声、缺失星和伪星等干扰条件下,算法识别率均高于原栅格算法且鲁棒性更强,体现出了很好的环境适应性。

下一步将围绕算法轻量化及高效性等方面进行数据处理流程和参数优化设计,以适应航空航天等平台应用的资源约束。