基于动态经济调度及无功调度的协同优化

许金炬

（国网江苏省供电公司江阴市供电分公司）

0 引言

电网调度对保障电网运行安全、降低电网运营成本、提升末端供电质量有积极帮助。随着智能电网覆盖范围的增加，对电网调度也提出了更高的要求。传统的电网调度只针对特定时段调度（即静态调度），无法解决发电机功率分配不合理的问题，实用性较差。本文基于不平衡功率分配方法，对传统的MHBA 算法进行了改良，运用该算法可实现全天候的动态经济调度和动态无功调度。运用该协同优化策略，不仅能避免以往电网调度中功率失衡等问题，而且还能改善电压质量、降低发电成本，对提升电力企业的经济效益有积极帮助。

1 动态经济调度数学模型的构建

经济调度的目的是在满足约束条件的前提下，使电网的发电成本最低、排放的污染气体最少。这里的约束条件包括2 项，其一是功率平衡等式约束，可表示为：

式中，Pi，t表示在t时刻第i个发电机的有功功率，Pd，t表示在t 时刻电网负荷，Ps，t表示t时刻的功率损耗。其二是发电机有功功率不等式约束，可表示为：

式中，和分别表示第i 个发动机输出的最大和最小有功功率。为了量化表示电网运行中发电成本和污染气体的排放量，设计目标函数：

式中，DFc（P）表示发电机在某个时间段（D）内的发电成本函数，对于火力发电机来说，特指燃料成本；DFe（P）表示某个时间段内污染气体排放函数。N表示发电机数量，ai、bi、ci分别是第i个发电机的成本系数，相应的xi、yi、zi为第i个发电机污染气体排放系数。本文把1h作为1个调度区间，一天内有24个调度区间，故T取值为24［1］。

2 动态无功调度数学模型的构建

无功调度的目的是合理分布无功潮流，达到降低线路功率损耗、保证电网运行安全的效果。与动态经济调度一样，动态无功调度的约束条件也分为等式约束和不等式约束。仅考虑无功功率的情况下，等式约束可表示为：

式中，Qi表示第i个发电机的无功功率；QDi表示节点i处的无功负荷；Gij和Bij表示节点i与j之间的电纳和电导。不等式约束条件有多种类型，如发电机电压约束、变压器抽头约束、无功补偿容量约束等［2］。这里以变压器抽头约束条件为例，不等式约束可表示为：

式中，t 表示变压器数量，Tt表示变压器交换头位置。为了量化表示动态无功调度效果，本文选取了“功率损耗”指标，并建立了目标函数，函数式如下：

式中，DFL（V）表示在某个时间段内的功率损耗函数，N表示线缆数量，gk表示第k条线缆的电导，Vi，t和Vj，t分别表示在t时刻节点i和节点j的电压幅值，λi，t和λj，t则为t 时刻对应节点的电压相角，这里的T同样取24。

3 动态经济调度和无功调度的协同优化策略

3.1 动态电网调度的协同优化模型

将前文所述的动态经济调度模型与动态无功调度模型相结合，构建动态电网调度协同优化模型，表示为：

式中，DFc、DFe、DFl的含义和表达式见上文，不在赘述。协同优化策略如下：

步骤1：结合电网参数，在发电机完成初始化后获取电压值V。根据V优化经济调度，计算出发电机的有功功率P和发电成本Fc。

步骤2：根据P，优化无功调度，计算出无功调度后发电机的电压值V1和功率损耗Fl。

步骤3：将V1作为经济调度的输入值，继续优化经济调度，求得新的P´、Fc´。

步骤4：将P´作为无功调度的输入值，继续优化无功调度，可以得到新的V1´和Fl´。

步骤5：重复上述步骤，直到满足条件［3］。

该协同优化策略可通过MHBA 算法（多目标混合蝙蝠算法）实现，从应用效果来看能够加快收敛速度、达到多目标优化目的。但是MHBA 算法通常适用于静态电网调度，如果将其直接运用到动态电网调度中，容易出现功率失衡、功率分配不均等问题，协同优化效果不理想。基于此，本文提出了一种改进的MHBA算法。

3.2 基于改进MHBA算法的协同优化

本文在传统MHBA 算法的基础上，用不平衡功率分配法对其进行改进，实现方法为：

步骤1：获取当前发电机的有功功率P，根据上文介绍的功率平衡等式求得不平衡功率，以error表示。

步骤2：设定一个阈值δ，并将error 与δ 对比，判断不平衡程度。如果存在error＞δ，则根据发电机数量（N）计算error的平均值，即error/N。

步骤3：把均分后的error 至分配给每一台发电机，此时发电机获得新的有功功率，记为Pi。

步骤4：重复步骤1～3，持续迭代，直到迭代次数m达到最大值（mmax），算法结束［4］。

改进的MHBA算法流程如图1所示。

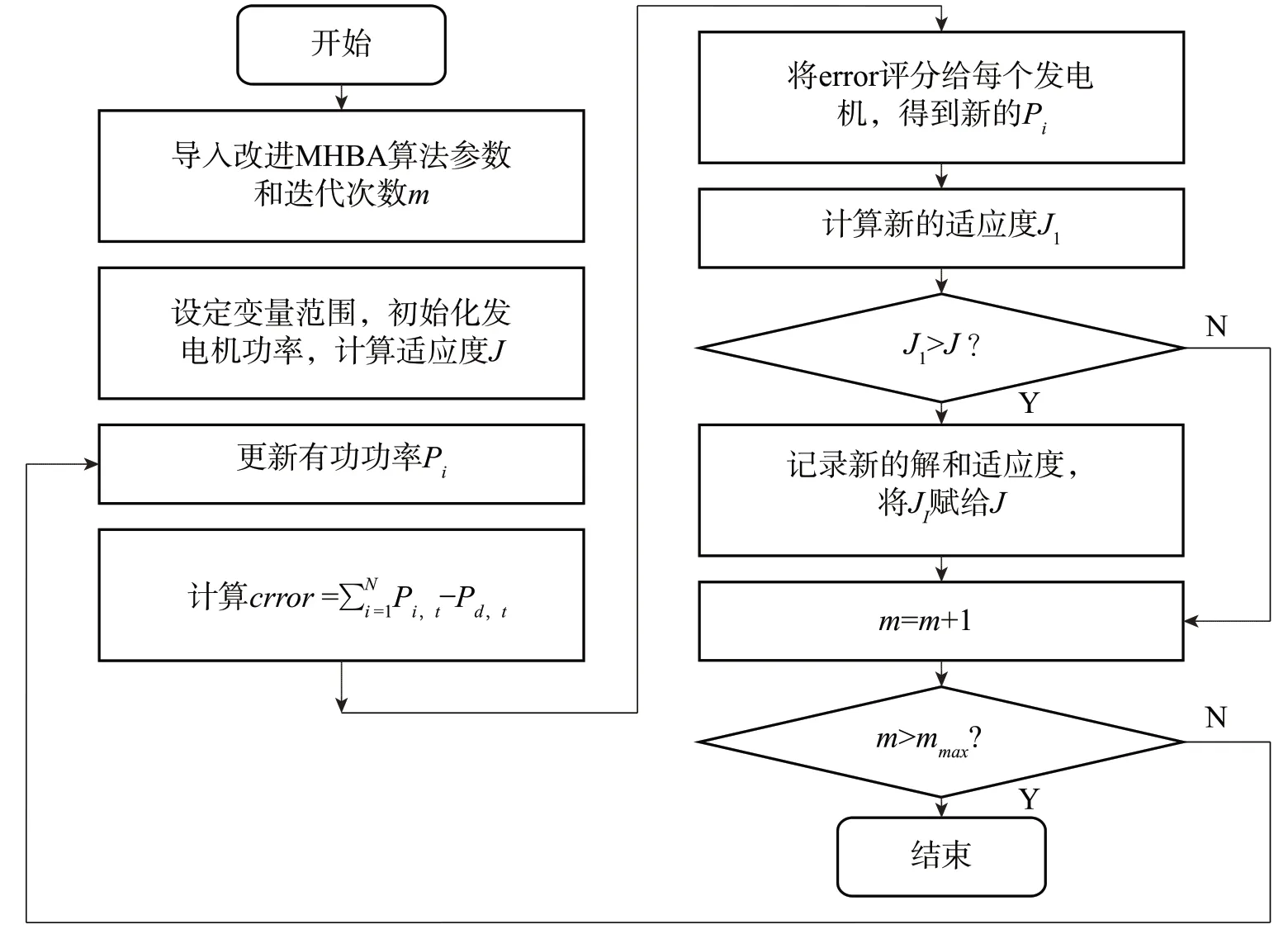
图1 基于改进MHBA算法流程图

4 基于协同优化策略的电网调度仿真分析

4.1 仿真实验设计

为了验证上文设计的基于改进MHBA 算法协同优化策略的应用效果，在Matlab R2020上进行了仿真实验。运行环境为：

操作系统Windows10； CPU： 3.12GHz Intel Core i7处理器；内存：16GB。

在仿真实验中，选择“发电成本”和“功率损耗”两项指标，评价传统MHBA 算法协同优化策略与改进MHBA 算法协同优化策略，在电网调度中的应用效果［5］。为了消除无关因素干扰，仿真实验中模拟了某电力系统在一天内各个时段的真实负载变化情况，如表1所示。

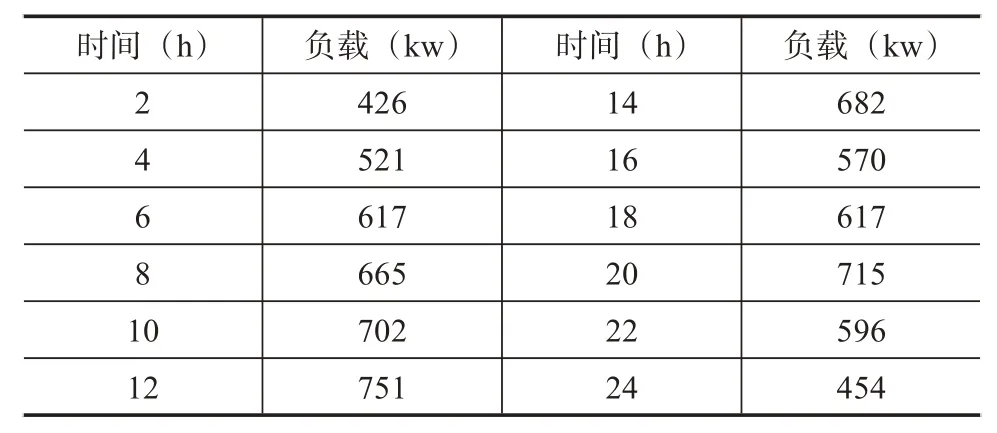
表1 某电力系统24 h负载记录表

4.2 仿真实验结果

仿真实验结果如图2所示。

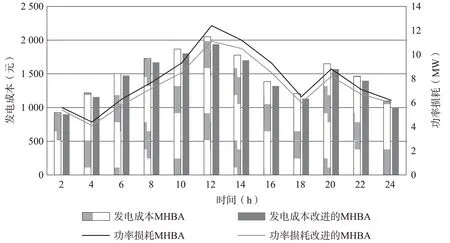
图2 两种算法协同优化下发电成本和功率损耗对比结果图

结合上图可知，在“发电成本”一项中，相比于传统MHBA 算法，使用改进MHBA 算法进行动态经济调度和动态无功调度的协同优化，电力系统每天的发电成本有明显的降低。在2h 时两者差异最小，为24 元；在14h 两者差异最大，为77 元。使用改进MHBA 算法协同优化策略后，该电力系统每天可节约发电成本（以平均值计）为：35748-34128=1620 元。在“功率损耗”一项中，相比于传统MHBA 算法，使用改进MHBA 算法进行协同优化后，电力系统的功率损耗也有一定程度的下降。在2h 和24h，两者功率损耗差异最小，为0.2kW；在12h 两者功率损耗差异最大，达到了1.3kW。使用改进MHBA 算法协同优化策略后，该电力系统每天降低的功率损耗（以平均值计）为：189.6-176.0=13.6kW。

根据仿真实验数据可知，本文提出的基于改进MHBA 算法的动态经济调度和动态无功调度协同优化策略，能够让电力系统的发电成本和功率损耗得到不同程度的降低，对降低电力企业的运维成本和提高供电质量有积极帮助。

5 结束语

在电力系统的运维管理中，电网调度是一项重要操作。随着电网智能化的成熟发展，将人工智能技术应用到电网调度中，在解决复杂调度问题和优化调度效果方面发挥了重要作用。在构建动态经济调度和动态无功调度协同优化模型的基础上，利用改进的MHBA 算法对目标函数求解，在人工智能技术的支持下进行多次迭代运损，逐步逼近最优解，保证了约束条件的最优化。在此基础上进行电网调度，显著降低了发电成本和功率损耗，在满足用户用电需求的同时，也达到了电力企业的预期。