数据挖掘和神经网络技术在电力工程造价领域的运用

刘乃新

（天津送变电工程有限公司）

0 引言

电力工程数据有着较高的复杂性，且数据量普遍较大，想要在前期实现更为精准的造价预测，以此为工程造价管理工作的高质量展开提供参考与指导，就需要形成一种能够在海量复杂数据中提炼、分析与处理有价值数据的方法，而应用数据挖掘和神经网络技术就能够达到上述目标。

1 数据挖掘和神经网络技术在电力工程造价领域的具体应用思路

1.1 使用数据挖掘算法收集与整理历史数据

应用数据挖掘方法，在海量电力工程数据内提炼出有价值数据信息，为提升整个数据提取的效率以及实效性，需要保证数据挖掘过程的完整性，如图1 所示。

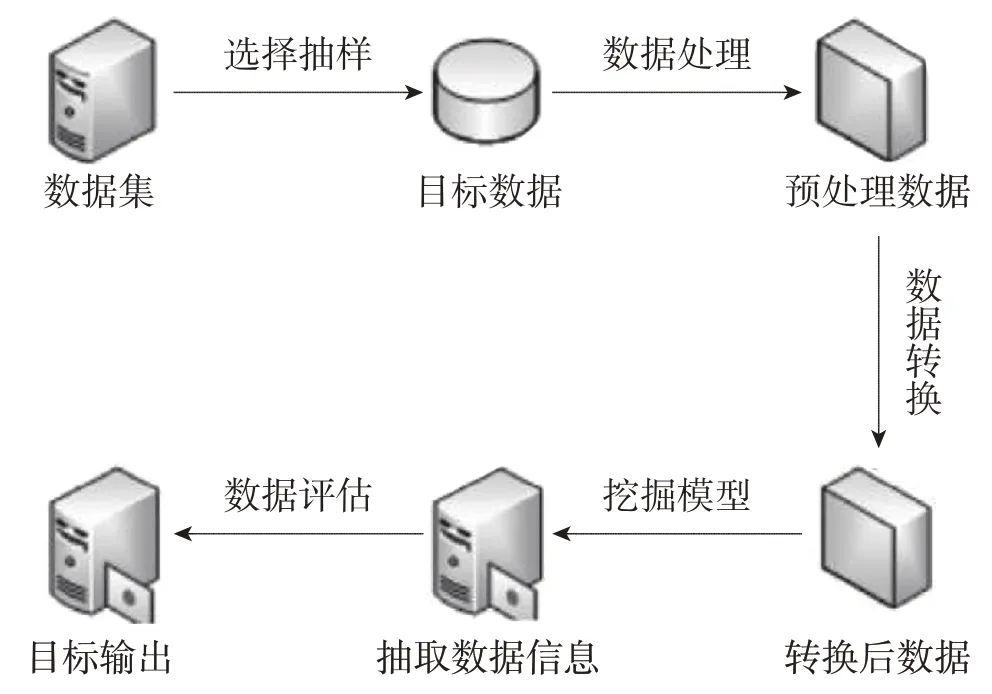
图1 数据挖掘流程安排

在当前的实践中，更常使用如下几种方法完成数据挖掘与处理，包括决策树法、统计分析法、神经网络法、遗传算法、模糊逻辑法等等［1］。相比较而言，由于模糊神经网络算法兼顾神经网络法以及模糊逻辑法的优势性，所以更适合在电力工程数据处理、工程造价预测方面应用。在此过程中，需要重点完成对模糊系统参数的获取以及模糊规则参数的识别。实践中，依托聚类法的利用，将数据空间划分为多个模糊数据集，并进一步结合训练得展开，形成隶属度函数，在此基础上获得所需要的输出数据。简单的模糊神经网络模型如图2 所示。

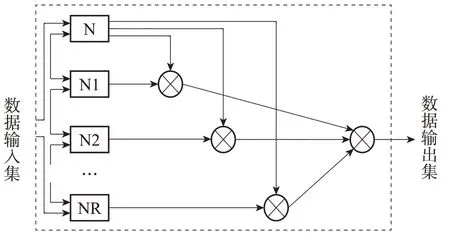
图2 简单的模糊神经网络模型图

在该模型图内，N1，N2... 代表着不同数据集的神经网络系统，其中，神经网络的主要功能在于，针对各个子网络的隶属参数进行精准辨识。各个子网络所代表着的模糊规则有所不同，在完成所有的子网络训练后，可以结合对应的权重，实现对网络最终输出的确定与形成［2］。

1.2 实施数据预处理

分析与处理电力工程造价数据期间，需要在较短时间内完成大量数据的有目的筛选，并在尽可能保持原始数据信息的基础上，确定出可以代表电力工程数据属性的数据集合［3］。一般而言，电力工程造价数据主要以数值的形式保存，所以可以应用贝叶斯分类器作为评价函数，假设S 为数据集，样本属性设定为X1，X2... ；使用C1，C2...表示现有数据种类；对于一个新的样本数据而言，其属于某一类C 的概率可以用下式确定：

式中，带宽使用h 表示；样本数使用nCj表示。

使用高斯分布函数对贝叶斯分类算法进行改进，得到的后验算概率计算公式如下所示。

式中，数据分布概率的高斯密度函数使用g 表示，均值为0，方差为1。以某电力工程造价数据为例，展开对100 个数据节点的评估，并在此基础上针对节点所对应着的数据属性进行规律汇总，所得到的电力工程输入数据集与输出数据集属性如下所示。

在输入集内，包含的属性有电力工程的电压属性、线路回路、地形系数、运输距离以及线路长度。在输出集内，包含的属性有运输工程造价、基础工程造价、架线工程造价、附件工程造价。

1.3 依托神经网络算法建立预测模型

结合前期对电力工程数据的分析能够了解到，受到输入与输出工程数据多元的影响，数据分析的本质可以理解为非线性映射问题。基于此，在选定分析与处理算法时，可以将电力工程造价数据处理的核心算法设定为模糊神经网络算法，并以此为基础落实对电力工行造价估算模型的构建［4］。

综合使用常规神经网络算法与模糊神经网络算法，兼顾模糊系统的推理功能以及数据学习功能，不仅可以获取到数据规则，还能够显现出更为强大的网络容错能力，在复杂性相对较强的非线性数据处理与分析方面可以发挥出更为理想的作用与优势。使用神经网络算法建立预测模型的主要流程安排如图3 所示。

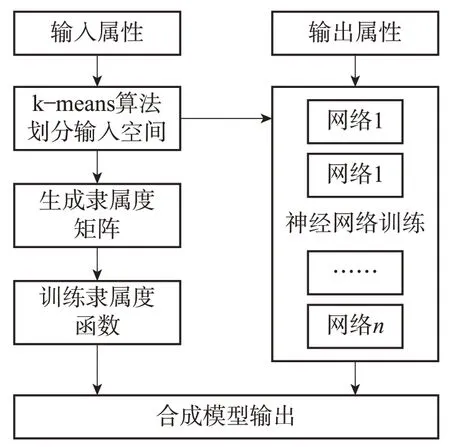
图3 使用神经网络算法建立预测模型的流程图

2 数据挖掘和神经网络技术在电力工程造价领域的应用实例分析

2.1 样本与案例的选择

选定经过数据预处理后的200 条历史数据作为电力工程数据的处理原始数据，输入数据内含5 种属性、输出数据内含4 种属性，主要如下所示（节选）：

样本1，输入属性集内含：电压等级为110kV，线路回数为1，运输距离为20km，地形系数为1，线路长度为200km；输出属性集内含：运输工程5.89 万元/km，基础工程2.36 万元/km，架线工程14.2 万元/km，附件工程0.89 万元/km。

样本2，输入属性集内含：电压等级为110kV，线路回数为2，运输距离为10km，地形系数为1.2，线路长度为250km；输出属性集内含：运输工程4.33 万元/km，基础工程3.56 万元/km，架线工程9.11 万元/km，附件工程0.15 万元/km。

样本3，输入属性集内含：电压等级为220kV，线路回数为2，运输距离为15km，地形系数为2.2，线路长度为300km；输出属性集内含：运输工程4.52 万元/km，基础工程8.98 万元/km，架线工程9.36 万元/km，附件工程0.47 万元/km。

样本4，输入属性集内含：电压等级为220kV，线路回数为2，运输距离为16km，地形系数为2.2，线路长度为300km；输出属性集内含：运输工程4.55 万元/km，基础工程8.78 万元/km，架线工程22.3 万元/km，附件工程5.66 万元/km。

样本5，输入属性集内含：电压等级为220kV，线路回数为2，运输距离为24km，地形系数为1，线路长度为300km；输出属性集内含：运输工程5.66 万元/km，基础工程7.41 万元/km，架线工程30.8 万元/km，附件工程1.23 万元/km。

2.2 实例分析方案与过程

针对上述电力工程数据，应用K-means聚类法展开进一步聚类处理，得到的分类结果如下所示：

在聚类1内，对象数目为30，输入属性聚类中心值内含：X1为199.7，X2为130.1，X3为14.26，X4为0.9，X5为0.61；输出属性聚类中心值内含：Y1为2.22，Y2为1.95，Y3为1.887，Y4为7.84。

在聚类2内，对象数目为30，输入属性聚类中心值内含：X1为265.7，X2为133.5，X3为0.68，X4为2.5，X5为0.13；输出属性聚类中心值内含：Y1为4.53，Y2为2.25，Y3为12.5，Y4为4.12。

在聚类3内，对象数目为30，输入属性聚类中心值内含：X1为304.2，X2为156.5，X3为12.1，X4为2.4，X5为0.33；输出属性聚类中心值内含：Y1为2.14，Y3为12.5，Y3为2.68，Y4为21.3。

在聚类4内，对象数目为30，输入属性聚类中心值内含：X1为203.1，X2为145.2，X3为11.5，X4为1.3，X5为0.22；输出属性聚类中心值内含：Y1为1.24，Y2为3.25，Y3为1.24，Y4为2.25。

在完成电力工程数据的分类后，使用模糊神经网络调整隶属度函数，在整个计算过程中，主要将选定的样本划分为3 部分，其中，训练集内包含的样本数量为120个；测试集内包含的样本数量为40个；验证集内包含的样本数量为4 个。进行500 次迭代后即可停止运算，以此获取到规则隶属度。进一步针对结果的相关性展开验证，确定出基于神经网络算法的输出结果以及实际网络输出结果之间存在着的相关性，如下表所示：

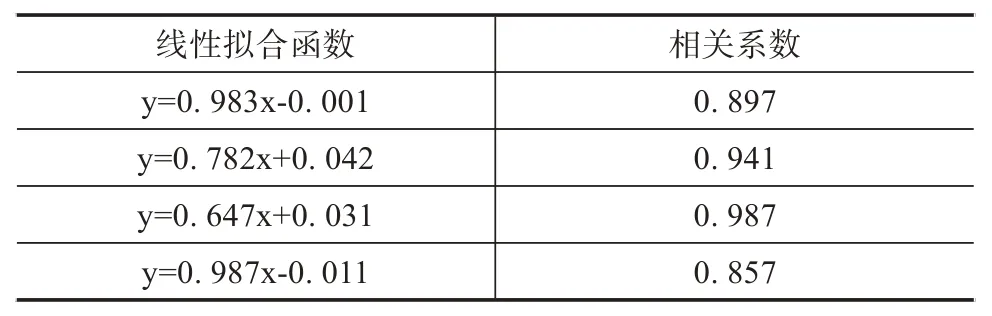
表1 网络N的回归分析结果汇总

2.3 分析的结果与结论

结合上述分析能够了解到的是，通过综合使用数据挖掘技术与神经网络技术，能够完成对电力工程造价数据的处理与分析，并在一定程度上，可以结合对模糊神经网络的使用获取到数据规则，以此为基础预测电力工程造价水平。使用模糊神经网络，针对选定的200 组历史数据展开数据规则的提取，并针对特定电力工程实施造价预测，所得到的仿真模拟分析结果如下所示：

模型1，得到的实际值包括：运输工程4.44 万元/km，基础工程5.54 万元/km，架线工程25.5 万元/km，附件工程0.57 万元/km；模糊神经网络预测值包括：运输工程4.25 万元/km，基础工程5.41万元/km，架线工程24.6 万元/km，附件工程0.46万元/km。

模型2，得到的实际值包括：运输工程4.53 万元/km，基础工程4.87 万元/km，架线工程15.2 万元/km，附件工程0.14 万元/km；模糊神经网络预测值包括：运输工程3.56 万元/km，基础工程4.25万元/km，架线工程14.2 万元/km，附件工程0.13万元/km。

模型3，得到的实际值包括：运输工程2.53 万元/km，基础工程1.65 万元/km，架线工程22.2 万元/km，附件工程0.15 万元/km；模糊神经网络预测值包括：运输工程2.45 万元/km，基础工程1.56万元/km，架线工程19.6 万元/km，附件工程0.15万元/km。

模型4，得到的实际值包括：运输工程5.65 万元/km，基础工程5.25 万元/km，架线工程14.2 万元/km，附件工程0.26 万元/km；模糊神经网络预测值包括：运输工程5.46 万元/km，基础工程5.33万元/km，架线工程15.2 万元/km，附件工程0.27万元/km。

模型5，得到的实际值包括：运输工程4.57 万元/km，基础工程4.25 万元/km，架线工程12.5 万元/km，附件工程0.24 万元/km；模糊神经网络预测值包括：运输工程4.33 万元/km，基础工程4.25万元/km，架线工程13.2 万元/km，附件工程0.28万元/km。

实际值与模糊神经网络预测值的平均相对误差为：运输工程0.074 万元/km，基础工程0.044 万元/km，架线工程0.0689 万元/km，附件工程0.094万元/km。

综合仿真模拟分析结果可以明确的是，基于上述方法所得到的预测值以及实际值的平均相对误差均保持在低于0.1 的水平，满足电力工程实际应用需要。这表明，综合使用数据挖掘与神经网络这种算法对于不同的电力工程造价数据均具备一定的分析应用能力，能够达到分析、预测电力工程造价数据的效果，并结合对历史数据的应用，向相关人员提供更具合理性的参考值，为电力工程造价数据处理以及工程实际应用提供有效指导与有价值参考。

3 结束语

综上所述，结合仿真模拟分析结果能够明确的是，通过使用数据挖掘算法收集与整理历史数据、实施数据预处理、依托神经网络算法建立预测模型，能够实现对复杂电力工程数据的分析与处理，所得到的预测值以及实际值的平均相对误差均保持在低于0.1的水平，满足电力工程实际应用需要；综合使用数据挖掘与神经网络这种算法对于不同的电力工程造价数据均具备一定的分析应用能力，能够达到分析、预测电力工程造价数据的效果。