基于MPMR方法的电力市场日前电价预测方法

胡如乐 郑 瑛 张建中

（南方电网数字电网研究院有限公司）

0 引言

在传统的电力行业垄断体制下，电价主要由政府机构制定，市场中的价格波动相对较小且较为稳定。然而，随着电力市场的自由化和市场竞争的推进，电价开始受到多种因素的影响，包括供需关系、燃料成本、天气条件、输配电网状况等。这使得电价表现出更高的变动性和不确定性。伴随着电力市场的开放和市场化改革，电力市场的参与者需要更好地了解和应对市场价格的波动。准确预测电价有助于市场参与者进行市场交易、电力规划和运营决策等，提高其竞争优势。而电价预测为电力市场参与者（如发电商、电力交易商、消费者等）提供了重要的信息和依据，有助于他们制定合理的电力市场策略和决策。准确的电价预测能够帮助市场参与者进行优化的运营调度、风险管理以及市场交易等，提高其商业竞争力。同时，电价预测对于实现电力供需平衡和电力市场资源配置的均衡也具有重要意义［1］。通过准确预测电价，可以为供应商和消费者提供合理的市场参考价格，鼓励资源配置的有效性和经济性，避免供需失衡和能源浪费。因此，许多相关学者对电力市场的电价预测进行研究，如：牛元有等人基于二次分解特征矩阵和PCNN-BiLSTM，研究短期电价预测［2］。采用完全集合经验模态分解的方法，将归一化后的原始电价/负荷数据分解成一系列分量。然后，我们使用变分模态分解得到模态分量。然后，利用第一次和第二次分解得到的所有分量构建了一个包含两个通道的输入特征矩阵。采用PCNN 法提取各种特征，并将这些特征融合在一起。最后，我们将融合后的特征输入到BiLSTM 预测结构中，以预测电价。郑宏等人基于LSTM 与XGBoost 组合模型研究电价预测［3］。选用法国电力市场2019 年1 月1 日至2020 年12 月31日的电价数据为训练集训练模型，对2021 年1 月1日不同模型预测的结果与实际电价值进行对比分析。但是上述方法缺乏一定的稳定性，长期运行中不能保证预测精度。

通过对历史数据的分析和建模，MPMR 方法能够提供相对准确的电价预测结果，并且在长期运行中能够保持一定的稳定性。对此，本文提出基于MPMR 方法的电力市场日前电价预测方法。

1 基于GCA 的周期性电力特征选择

GCA 方法可以更准确地捕捉电力市场的周期性变化模式。将这些特征作为输入，结合MPMR方法进行分类和回归分析，可以构建更准确和可靠的日前电价预测模型，帮助电力市场参与者做出更好的决策和规划［4］。灰色关联分析的关联性越高，表明两个数据序列更加接近，相关性更强因此，选择GCA 对电价数据进行周期性重要样本和重要特征选择。GCA 算法基本计算流程为：

（1）将输入样本集设定为一个矩阵D，即为比较序列：

式中，λn(k)表示输入样本数据第k个样本的第n个特征。

（2）若目标序列表示为λ0，其表达式为：

（3）对输入数据进行标准化后，即可采用式（3）计算出D和λ0间的灰色关联度，具体表示为：

式中，Δmin和Δmax分别表示各列差值的最小值和最大值，Δoi(t)表示参考序列与第i个比较序列差值的绝对值；ξ表示分辨系数。

（4）由此得到最终的灰色关联度表达式为：

基于上述灰色关联度计算结果根据关联度高低进行序列删选和保留。

2 基于MPMR 方法的电力市场日前电价预测模型构建

基于上的获取的周期性电力特征，采用MPMR方法创建电价预测模型［5］。该方法的核心思想是构建一个二元分类器，以确定输入数据点属于哪个类别，二元分类器的形式如下：

合适的γ值能够使得分类器更准确地进行分类，对电价预测模型的质量起到积极影响，通过求解最优化问题的数值方式，可以得到γ：

利用式（7）得出bc的数值，确定合适的bc值可以使模型输出更准确地反映电价预测结果：

通过分析最小最大概率回归，可以构建MPMR方法的框架。通过应用这个框架，可以将原始训练样本数据集F 划分为两种类型的数据，从而有助于在回归模型中提取有效的特征信息，从而更精确地进行电价预测，两种类型数据的表达式为：

通过确定两个点集，利用式（6）可以获得这两个点集的Rd+1值。根据Rd+1可以得到两类电极ui、vi分类面，进一步优化分类结果，使分类面能够更好地区分出不同类别的数据点：

计算符合式（9）的回归模型输出值，这些输出值可以作为电价预测的结果。其中z=（ŷ，x1，x2，…，xd）。即zj=uj（i=1，2，…，N）。为了避免使用非线性优化技术，通过式（9）来求解ŷ。在这个求解过程中，我们需要限定核函数Kc(zi，z)满足特定条件：

公式Kc(xi，x)=ϕ(xi)ϕ(x) 符合mercar 条件和函数。如此一来，求解最优γ值问题便可以变换成为线性最小二乘问题：

F∈R2N×(2N-1)为正交矩阵。将最优值问题转换为线性最小二乘问题，并得到正交矩阵。这有助于简化模型的求解过程，并帮助提高模型的计算效率和鲁棒性。基于上述流程实现电力市场日前电价预测。

3 实例分析

3.1 实验环境

为验证构建的电价预测模型是否可行，实验仿真平台选用MATLAB R2016a。实验配置为Inel（R）Core（TM）i5-4210U CPU@1.70GHz，64 位，内存大小为128G。为取得更好的实验效果，实验选择某电力市场2020~2022 年不同时间段20 种类型的电价特征共计55000 个。

3.2 实验指标

为更好地对模型预测效果进行评估，实验选择平均绝对预测误差为评价标准进行对比测试，表达式为：

式中，n表示含有n个预测电价。Y、Yi代表预测范围实际电价与预测电价。

3.3 实验结果

基于上述实验环境与实验指标的设置，采用本文方法、文献［2］方法与文献［3］方法进行对比测试，结果如下图2 所示。

根据图1 可以看出，本文方法的电价预测误差最高仅为0.02，对比方法的电价预测误差最高分别为0.34、0.41，由此可见，本文方法的电价预测误差明显低于对比方法，说明本文方法的电力市场日前电价预测性能较高。

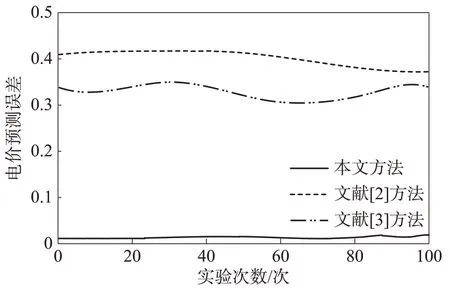
图1 电价预测误差对比结果

为进一步验证设计方法是实用性，进行电价预测时间的实验测试，测试结果如下表1 所示。

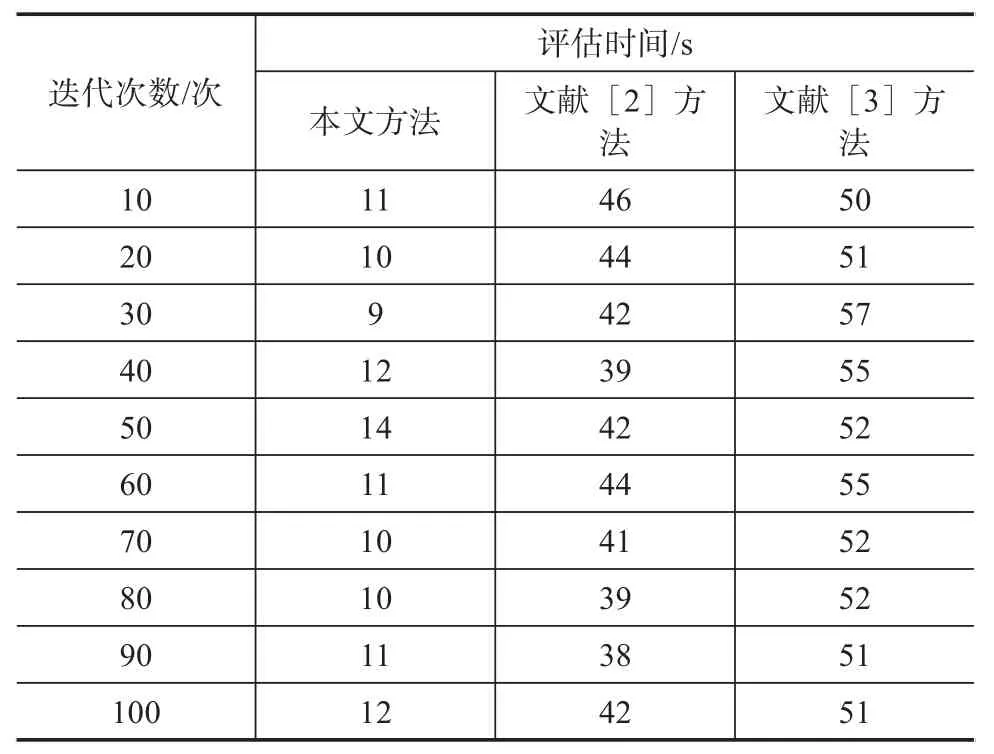
表1 三种方法的电价预测时间结果

根据上述表格可以看出，本文方法的电价预测时间最高为14s，对比方法的电价预测时间最高分别为46s、57s，由此可见，对比方法的电价预测时间明显高于本文方法，由此可见，本文方法的电价预测效率较高，能够为日后的电价预测提高帮助。

4 结束语

伴随着电力市场的开放和市场化改革，电力市场的参与者需要更好地了解和应对市场价格的波动。准确预测电价有助于市场参与者进行市场交易、电力规划和运营决策等，提高其竞争优势。设计方法首先通过计算灰色关联度来量化电价数据与其他特征之间的关联性，选取与电价具有较强相关性的特征。然后，基于获取的电价特征利用MPMR 方法构建电力市场的日前电价预测模型。实验结果表明：本文方法的电价预测误差最高仅为0.02，本文方法的电价预测时间最高为14s，说明设计方法的电价预测误差较低且预测时间较短，有助于提升电力市场的运行效果和决策质量。