电力负荷需求与经济指标的相关性分析

杨耿琦

（国网孝感供电公司变电运检分公司）

0 引言

近年来，学术界对电力与经济发展的相关性展开了深入的研究，也取得了一定的成果。大部分研究结果表明电力与经济具有紧密的联系。电力是经济发展的基础，而经济发展又是电力发展的主要动力，两者都具有自身的发展规律，但又具有相辅相成的关系，从而形成了一个极为复杂的体系。

文献［1］通过协整分析检验了国内生产总值和电力消费间的长期稳定均衡关系，同时探讨了对这一均衡关系的具体影响因素。文献［2］探讨了我国电力和经济之间的单向关系，并探讨了具体的预测方法。文献［3］通过构建系统动力学的状态空间模型，分析了电力需求和国内生产总值增长率的具体关系，利用计量经济模型对电力需求增长率进行了预测分析。文献［4］基于低碳经济目标下，以国内生产总值、单位生产总值碳排放量以及人口和单位生产总值能耗为变量，通过回归分析法对具体条件下的电力需求进行了预测分析。文献［5］通过构建偏最小二乘回归模型，以固定资产投资、生产总值以等为相关指标，对某地区的电力需求进行了预测。文献［6］通过协整分析与向量误差校正模型，对我国电力需求和人口、GDP 以及固定资产投资等之间的长期均衡关系进行了分析，并利用Granger 因果关系检验了我国电力需求与各项指标之间的因果关系。文献［7］采取实证分析与统计分析的方式，分析了产业结构对电量需求的具体影响。

在当前的经济发展新常态下，我国的经济增长发生了较大的变化，从而也影响到了各地的用电需求变化。对此，我国政府必须要在宏观层面对电力进行科学规划，以此确保电力行业的可持续发展。而科学规划首先就需要准确的预测电力需求，正确认识电力需求与经济发展之间的相关性。基于此，本文以某省为例，通过主成分分析法对该省的电力负荷需求与经济指标的相关性展开分析，为电力需求分析预测提供理论依据。

1 理论基础

1.1 回归分析法

回归分析法指的是利用数理统计法，根据所掌握的大量数据，以此构建因变量和自变量之间的回归方程式，是对信息的分析和预测。根据所研究的因果关系涉及到的自变量数量可以分为一元回归分析和多元回归分析两种，即自变量为一个时则为一元回归分析，多个自变量则为多元回归分析；而按照描述自变量和因变量因果关系的函数表达式性质可以分为线性和非线性两种。为了确保回归方程尽可能的符合实际情况，要准确判断自变量的数量与具体种类，同时根据事物的发展规律定性判断定性回归方程的类型。

1.2 多元统计分析法

多元统计分析法实际上就是一种综合分析方法，目前还没有明确的概念和具体的分类，其可以对多组变量进行同步分析及处理，能够对事件的特征及发展规律进行总体概括，核心内容为修正与统计推断总体参数估计，主要体现在各种统计方法的应用上面，包括典型相关分析、判别分析、主成分分析、聚类分析等，是深层次经济分析的一种有效工具。

2 电力需求与GDP的相关性分析

回归分析法是电力系统负荷预测常用的一种预测方法，从可持续发展角度来看，一个地区的电力需求受到当地经济环境直接的影响，而GDP 又是体现该地区经济发展水平的主要依据。本文收集某省2013-2022 年这段时期的年总用电量与GDP 相关数据资料，以此进行相关性分析，结果显示该省GDP 与电量值的相关系数为0.993，也就表示该省电力需求与GDP 具有相关性，可以作为回归分析当中的回归因子。因此，通过深入分析GDP 水平对电力需求的具体影响，明确该省电力需求与经济发展之间的相关性，为当地电力需求分析及预测提供参考依据。首先，对相关数据进行常规处理，消除异方差的影响，确保原序列单调性质的稳定性，减少原序列中信息量的损耗。

如图1 所示，从2013 年-2022 年某省用电量增速与GDP 增速变化曲线可以看出，该省的用电量与GDP 呈正比关系，即用电量随着GDP 的增长而增长，具有极强的关联性。针对该省的用电量Load以及GDP进行线性回归分析，具体如下：

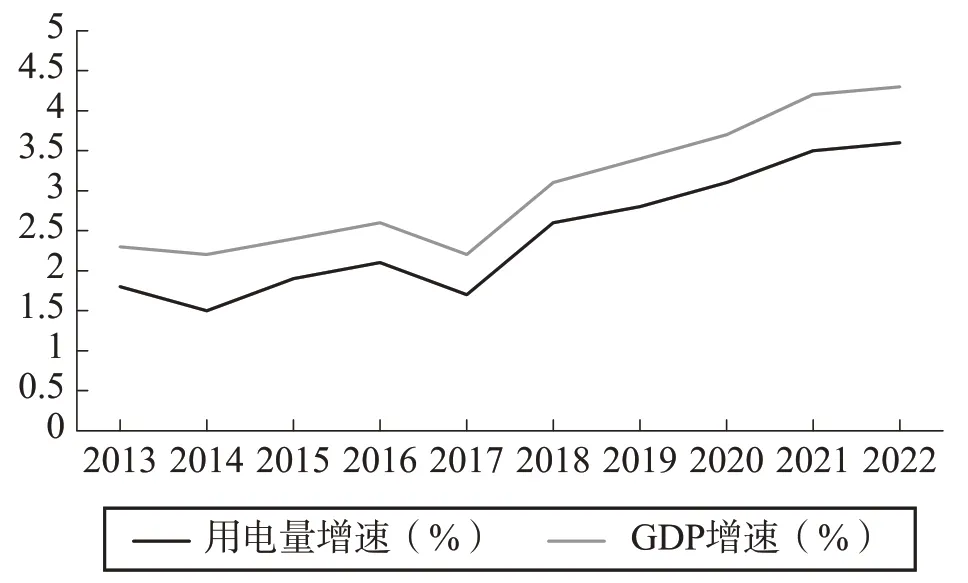
图1 某省用电量与GDP 变化曲线

得出该方程的拟合优度2R 值是0.9862，F 检验值是1142.450。

3 电力需求多影响因素分析

3.1 分析步骤

（1）收集整理P维随机向量X= (x1，x2，...xp)的n个样品x1= (xi1，xi2，...xip)，以此建立观察资料矩阵X= (xij)n*p；

（2）对样本阵当中的原始资料进行预处理，即将原始数据转换成正指标，对数据进行标准化处理，以此构建标准化矩阵；

（3） 对以上矩阵的样本相关系数矩阵R进行测算；

（4）对样本相关系数矩阵R的特征方程进行解析，以此获得P个特征值；

（5）获得主成分。

以上具体流程如图2所示。

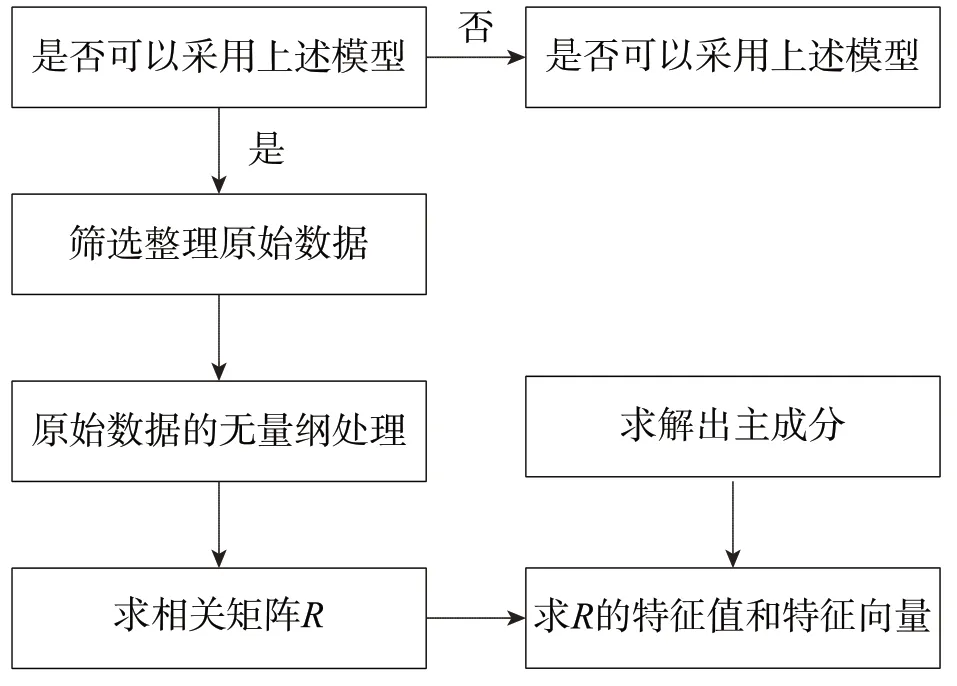
图2 主成分分析流程图

3.2 计算步骤

按照主成分的基本特征，其具体计算步骤如下：

（1）首先在下列公式中输入样本的观测值：

（2）根据式（3）、（4）对相关指标的样本均值以及样本标准差进行计算：

（3）对Xij进行标准化处理，对样本相关矩阵进行计算：

因为rii= 1，其rik=rki，故由此可知，R 为对称阵，所以，其对角线当中的元素均为1，需要对以下三角阵进行计算：

（4）对R的特征值和特征向量进行计算，若是可以通过正交换Q得出以下矩阵：

即R 的P个特征值则为λ1，λ2，...，λp。

假定λ1≥λ2≥... ≥λp> 0，那么，Q 的各列lj=也就是与λj对应的正规化特征向量。

（5）构建主成分

式中，Y1，...，YP为标准化指标变量。

（6）对前k个主成分样本值进行计算：

由此获得样本值(Zij)n×k，以此进行统计分析。

3.3 算例分析

为进一步明确各相关因素对电力负荷需求的具体影响，采取主成分分析方式对电量和相关影响因素展开分析，具体结果如表1所示。

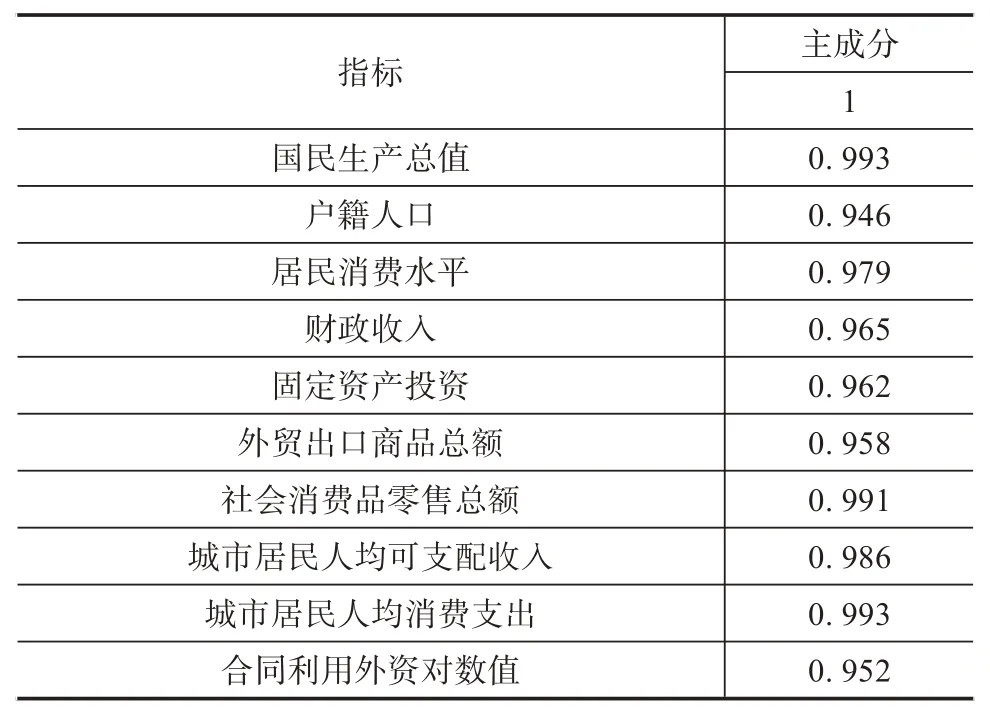
表1 主成分矩阵

有1 个主成分的特征值大于1，对总方差的累计贡献率达到了94.751%，选取1 个主成分，应用主成分分析法明确电量值最大影响因素。具体表达式如下：

式中，X1表示国民生产总值，X2表示年末户籍人口，X3表示居民消费水平，X4表示财政收入，X5表示固定资产投资，X6表示外贸出口商品总额，X7表示社会消费品零售总额，X8表示城市居民人均可支配收入，X9表示城市居民人均消费支出，X10表示合同利用外资对数值。由此得知主成分的代表范围为94.751%，所占比例较大，即主成分比较可以体现出综合经济指标列的具体情况，可以作为原本指标的影响因素进行分析。

通过主成分分析得出，该主成分和电量之间的相关系数为0.974，通过统计分析获得该省的电量值和该主成分因子的二次曲线回归关系，具体如下所示：

式中，Y表示的是该省的电量对数值，F1表示的是第一主成分因子。

根据主成分分析结果显示：该省的国民生产总值、社会消费品零售总额以及城市居民人均消费支出的相关系数均大于0.99，也就表明这三个因素是影响该省电力负荷需求最大的因素。

4 结束语

本文以某省为例，深入分析了该省电力负荷与经济指标的相关性及具体的影响因素，通过回归拟合结果显示：该省的电力负荷需求与经济指标之间具有较强的内在关联。同时，本文通过构建多元回归分析模式得知，国民生产总值、社会消费品零售以及城市居民人均消费支出是影响该省电力负荷需求的主要因素。