高压输电线路电场强度及磁通密度的计算

邓峰利

（广西绿能电力勘察设计有限公司）

0 引言

输电线路电压值过高导致了明显的电场强度增大，高压架空输电线路产生的电场强度存在许多问题，如应满足的规定参考值、导致交流电晕放电的问题等。当由于输电线路导线表面的电场强度较高，周围的空气被电离时，就会发生交流电晕。当架空输电线路导线表面的电场强度超过周围空气的击穿强度时，就会发生电晕放电，这种电场强度称为交流电晕起始电场强度［1-2］。在高压架空输电线路上发生交流电晕有几种影响，其中包括一些问题，如音频噪声和光效应，会给人带来不适，而另一方面，电磁干扰和电晕功率损失是技术问题。为了更好地了解这些过程，确定架空输电线路导体表面电场强度以及电晕起始电场强度的准确值很重要。

1 计算分析

本文中提出的电场强度计算是使用CSM 方法进行的，而磁通密度计算是使用基于BS 定律的方法进行的，这两种方法的二维算法最常用于计算架空输电线路产生的电场强度和磁通密度。下面将介绍这两种计算方法。

1.1 CSM计算

根据CSM 方法，电场强度源是假想的点电荷，每个导体可以由至少一个假想的点电荷表示，当导体用大量的假想点电荷表示时，可以获得更准确的结果。在计算导体表面的电场强度时，假想点电荷的数量尤其重要，这是考虑电晕现象所必需的，虚拟点电荷的相位可以根据其几何位置和相应的电势相量通过以下方程确定：

式中，q1⋅⋅qn是虚点电荷相量；ψ1⋅⋅ψn是对应于每个假想点电荷的电势相量；P11⋅⋅Pnn为势能系数；n表示虚拟点总数。

势能系数可由以下方程式确定：

式中，ζ0表示空气的介电常数；(xi，yi)是第i 个假想点电荷坐标；(xj，yj)表示第j个计算点的坐标。

一旦通过求解方程（1）计算出假想点电荷相量，在任意计算点的电场强度相量的矢量分量可以根据以下方程确定：

式中，Ex(x，y) 和Ey(x，y) 是电场强度相量的矢量分量，qi是第i个假想点电荷相量。(xi，yi)表示第i个假想点电荷的坐标；(x，y)分别是电场强度计算点的水平坐标和垂直坐标。

任意计算点的电场强度均方根（RMS）值定义如下。

1.2 BS计算

磁通密度计算采用基于BS 定律的方法。类似于使用虚拟点电荷作为电场强度源的CSM 方法，基于BS 定律的方法使用电流点源来确定磁通密度，增加布置在架空输电线路导线上的电流点源的数量可以得到更准确的磁通密度计算结果。根据先前所述，放置在第k个导体上的第j个电流点源的电流强度定义为：

式中，Ij是第k导体上的第j个电流源的电流强度，Ik表示第k导体的电流强度；ns是第k个导体上的点电流源的数量。

输电线路附近任意计算点的磁通密度相量的空间矢量分量由以下方程定义：

式中，坐标为(x，y) 的任意计算点处的磁通密度相量的空间矢量分量由Bx(x，y) 和By(x，y) 表示，ν0是空气的磁导率，Ii表示第i个电流点源的相量，(xi，yi)是第i个点电流源的坐标，n为电流点源总数。

任意计算点处的磁通密度的RMS 值可以通过以下等式来确定：

处理束导体时，通常将每个束导体视为放置在等效导体中心的一个假想点电荷或电流点源。通过分别利用更多的虚拟点电荷和点电流源，提高了电场强度和磁通密度的计算精度。为了获得更精确的电场强度和磁通密度计算结果，本文通过用几个虚拟的点电荷和点电流源表示每根绞线来进行计算。虚拟的点电荷和电流点源均匀地分布在每个绞线上以中心点为圆心的圆上。当处理电场强度计算时，区分虚拟点电荷位置和计算点位置是十分重要的，假想点电荷放置在半径为rc= 0.75·rw的圆上，中心位于绞线中心，其中rw是绞线的半径。另一方面，计算点被放置在半径等于绞线半径rt=rw的圆上，这使得在计算电势系数时以及在计算架空输电线路导体表面上的电场强度时能够克服奇点问题，在计算磁通密度时，电流点源的放置方式与计算电场强度时的计算点相同。

2 实验分析

将上述方法应用于220kV架空输电线路变电站产生的电场强度和磁通密度的计算。仿真计算了电场强度和磁通密度，并与现场测量结果进行了比较，进行现场测量时，测量所有架空输电线路导线的高度，电场强度和磁通密度的测量是在地面以上1m 的高度，在横向剖面上进行的。

在测量过程中，从SCADA 系统获得了线间电压和相电流强度的实际RMS 值，分别为226kV 和85.7A，该线间电压与相电流强度用于电场强度和磁通密度的计算。跨中附近横向剖面上的电场强度和磁通密度计算结果与现场测量结果的比较如图1 所示。此外，所考虑的横向剖面上所有点的计算结果和测量结果之间的绝对误差如图2 所示。由于所考虑的横向剖面末端的值较低，特别是在磁通密度的情况下，绝对误差被用作计算值和测量值之间偏差的度量。从图1 和图2 中可以注意到，计算和测量的电场强度和磁通密度结果之间存在微小的偏差。

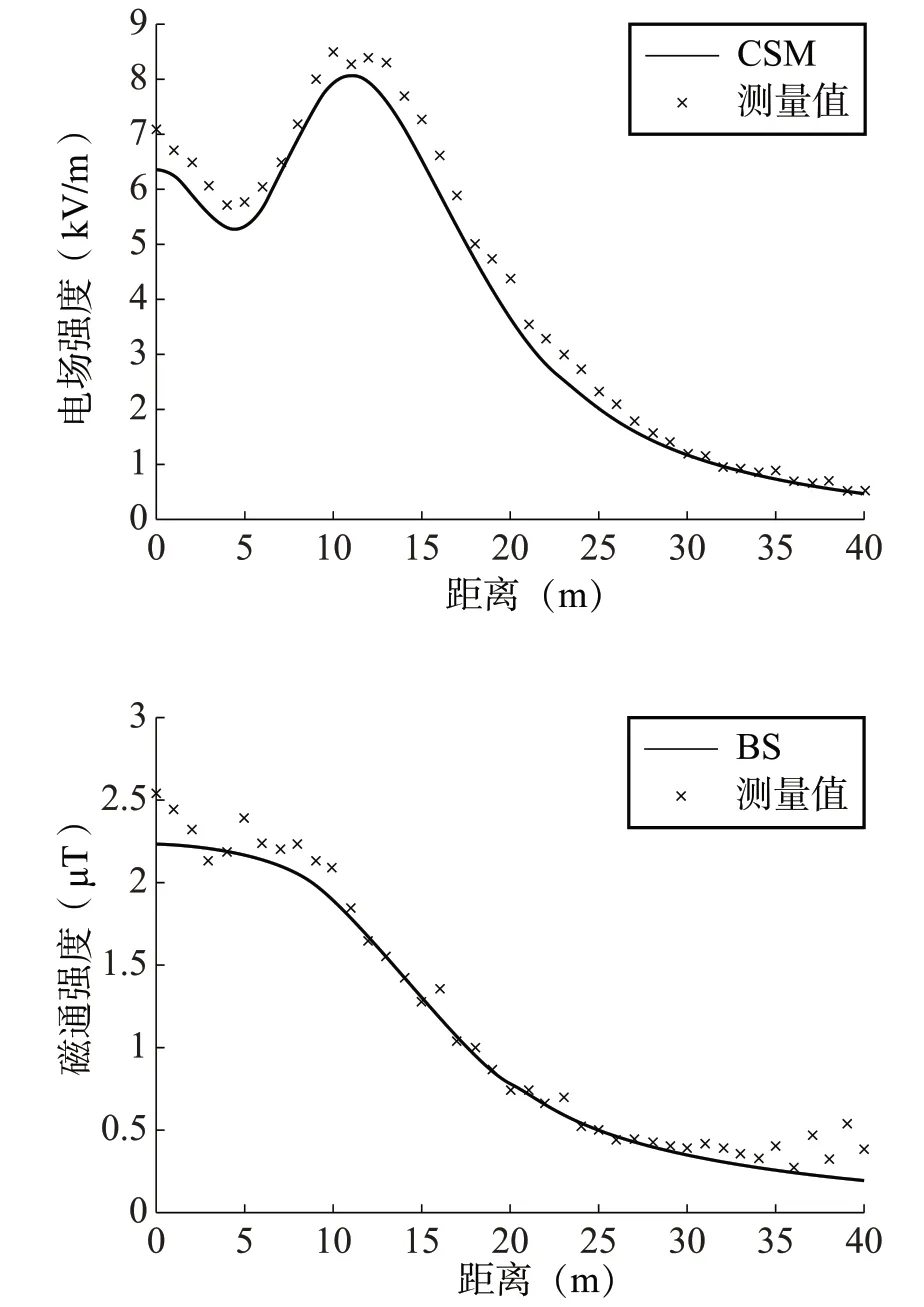
图1 横向剖面计算和测量结果的比较

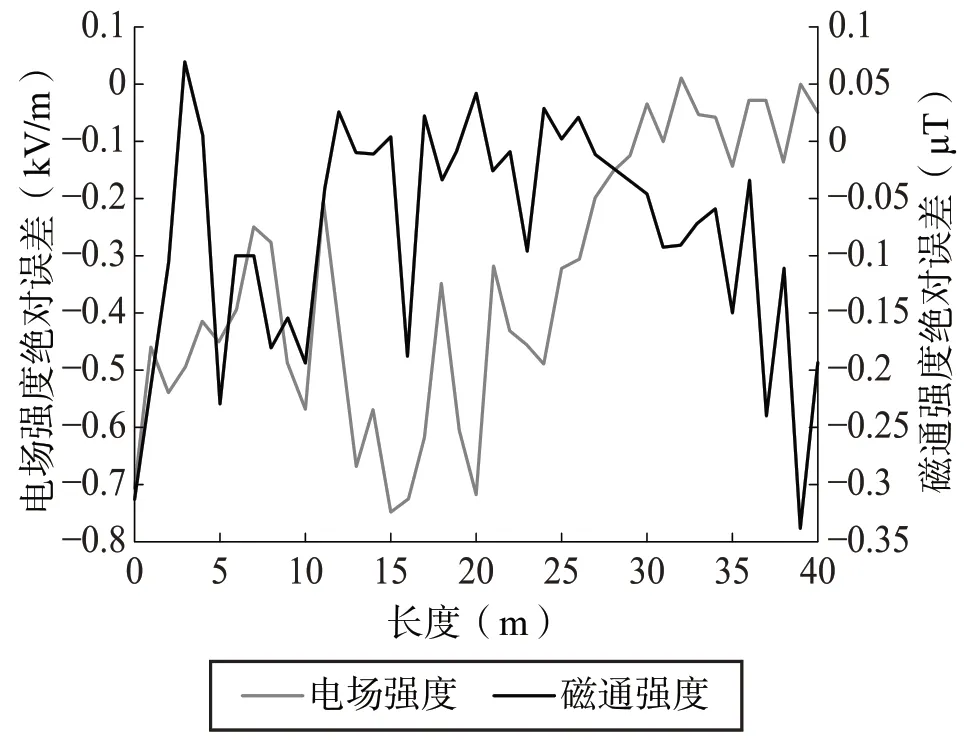
图2 计算结果和测量结果之间的绝对误差

针对分析的架空输电线路，计算了导线附近和导线表面上的电场强度。对于现场测量期间记录的实际环境压力和温度，还计算了交流电晕起始电场强度。

在图3 中，将导体表面附近的电场强度与交流电晕起始电场强度进行了比较。通过分析可以得到，导体附近的电晕放电条件得到满足，即实际电场强度超过交流电晕起始电场强度，考虑到在现场测量过程中记录了电晕放电的存在，计算结果达到预期效果。

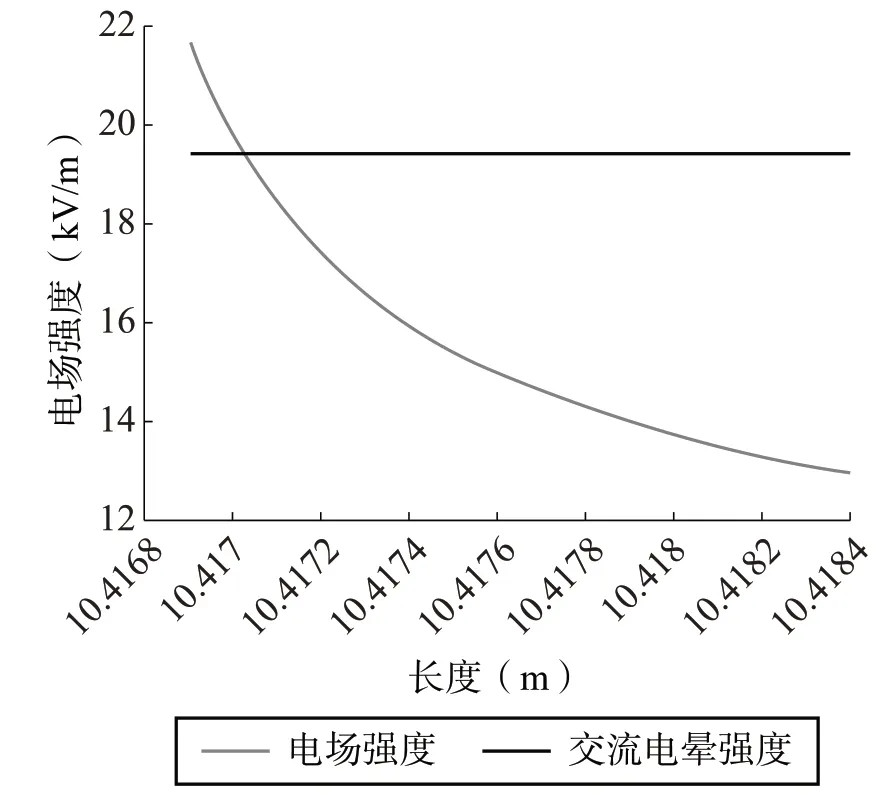
图3 导体附近的电场强度分布

导体表面上的电场强度分布如图4 所示。从图4中可以看出，导体表面上的电场强度分布可能会显著变化，这取决于导体表面上观察点的位置。

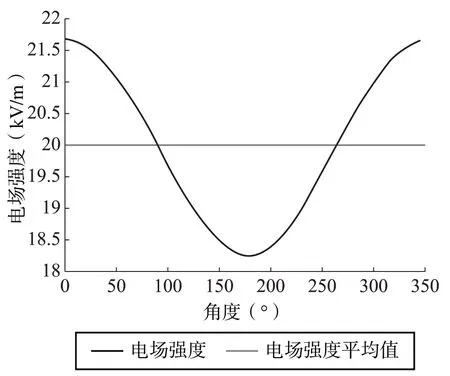
图4 导体表面的电场强度分布

3 结束语

本文考虑了架空输电线路产生的电场强度和磁通密度的计算方法。所提出的方法基于CSM 和BS定律方法的更精确的二维算法，这需要在每条绞线上使用几个假想的点电荷和电流点源。使用所考虑的方法能够更真实地表示束导体，并避免电场强度计算中的奇异性问题。由于高压架空输电线路面临电晕放电问题，本文还研究了导体表面附近电场强度的计算，并考虑了交流电晕起始电场强度的计算，将计算结果与220kV 架空输电线路横向剖面的现场测量结果进行了比较。结果表明，所考虑的计算方法可用于准确计算架空输电线路产生的电场强度和磁通密度。