基于特征点动态选择的三维人脸点云模型重建
陈素雅 何宏

收稿日期:2023-06-09;修回日期:2023-08-07 基金项目:国家科技部资助项目(G2021013008);上海市科学技术委员会资助项目(18070503000);上海理工大学医工交叉重点资助项目(1020308405,1022308502)
作者简介:陈素雅(2000—),女,安徽滁州人,硕士,CCF会员,主要研究方向为人工智能、人机交互系统;何宏(1973—),女(通信作者),四川人,教授,博导,博士,主要研究方向为医学人工智能、人机交互系统、医疗大数据分析(hehong@usst.edu.cn).
摘 要:針对典型的点云配准方法中伪特征点过多导致配准效率低和配准结果不精确的问题,提出一种基于特征点动态选择的三维人脸点云模型重建方法。该方法在粗配准阶段,采用动态特征矩阵求解法获取粗匹配特征变换矩阵以避免伪特征点的干扰。在精配准过程中,采用二次加权法向量垂直距离法在人脸流形表面选择更有效的特征点以减少伪特征点的数量,并采用基于特征融合与局部特征一致性的迭代最近点方法进行精配准。经过对比实验验证了算法的可行性,实验结果表明,该算法能够实现高精度且快速的三维人脸点云模型重建,且均方根误差达到1.816 5 mm,相较其他算法,其在模型重建精度和效率方面都有所提升,具有良好的应用前景。
关键词:三维人脸点云模型重建; 动态特征矩阵; 二次加权法向量垂直距离; 特征融合; 局部特征一致性
中图分类号:TP391.41 文献标志码:A
文章编号:1001-3695(2024)02-047-0629-06
doi:10.19734/j.issn.1001-3695.2023.06.0279
3D face point cloud model reconstruction based ondynamic selection of feature points
Chen Suya, He Hong
(School of Health Science & Engineering, University of Shanghai for Science & Technology, Shanghai 200093, China)
Abstract:Aiming at the problems of excessive pseudo feature points can lead to low registration and imprecise registration results in typical point cloud registration methods, this paper proposed a 3D face point cloud model reconstruction method based on dynamic selection of feature points. This method used the dynamic feature matrix solving method to obtain the coarse matching feature transformation matrix during the coarse registration phase, which avoided the interference of false feature points. In the fine registration process, it used the second-order weighted normal vector perpendicular distance method to select more effective feature points on the face manifold surface to reduce the number of false feature points. And it also used the iterative closest point method based on feature fusion and local feature consistency for fine registration. Comparative experiments verified the feasibility of the algorithm. Experimental results show that the proposed method can achieve high-precision and fast reconstruction of three-dimensional face point cloud model. And the root mean square error reaches 1.816 5 mm. Compared with other algorithms, the proposed algorithm can improve the accuracy and efficiency of model reconstruction, and has good application prospects.
Key words:3D face point cloud model reconstruction; dynamic feature matrix; quadratic weighted normal vector vertical distance; feature fusion; local feature consistency
0 引言
三维人脸因具有良好的成像不变性质,被广泛应用于人脸识别[1]、头位姿估计[2]以及智能医疗辅助诊断[3]等领域。根据数据来源的不同,可以将三维人脸重建分为两类:a)基于二维数据的三维人脸重建[4,5],直接从二维图像中提取人脸信息进行重建,然而这种方法往往依赖于先验知识,存在重建结果精度低、缺乏真实感和适用范围有限等问题;b)基于多视角RGB-D图像的三维人脸重建,利用深度相机采集多个角度的彩色图像和对应的深度图像,通过提取人脸点云的关键信息,融合多个角度的点云来实现三维人脸點云模型的重建。这种方法在二维图像的基础上引入了深度信息,增加了信息维度,使得重建后的三维人脸具有更高的精度、真实感及适用范围。目前,基于多视角RGB-D的三维人脸重建方法已成为主流方法之一。
基于多视角RGB-D的三维人脸点云模型重建主要是以不同帧下的公共区域为基础,将不同空间、时间下获取的各角度人脸深度信息整合到同一坐标系下。其中,最经典且应用最广泛的是Besl等人[6]提出的迭代最近点(iterative closest point,ICP)算法,然而,该算法只适用于处理小规模的点云数据,对点云初始位置依赖性强,易陷入局部最优,并且伪特征点过多易导致配准效率低、产生误匹配和配准结果不够精确。针对ICP算法易陷入局部最优的问题,研究人员通过粗配准为精配准提供良好的初始位姿。针对ICP算法因伪特征点过多导致配准效率低和配准结果不够精确的问题,研究人员通过提取对象表面的几何特征[7~9]或纹理特征[10~12]来减少伪特征点的数量,再使用ICP算法及其变体进行点云模型重建。黄际玮等人[7]提出基于几何特征内部形态描述子提取特征点进行粗配准,再采用法向量夹角约束改进的ICP算法完成精配准。单丽杰等人[8]提出基于几何特征法向量夹角提取三维空间关键点实现精配准。张泽鹏等人[9]提出基于快速特征点直方图提取点云特征实现重建。针对ICP算法因伪特征点易产生误匹配的问题,研究人员提出基于法向量夹角约束[7]、边长比例关系约束[13]等方法剔除误匹配点对。然而,上述方法仍存在伪特征点过多导致配准效率低和配准结果不够精确的问题,无法实现高精度且快速的三维人脸点云模型重建。
针对上述问题,本文提出了一种基于特征点动态选择的三维人脸点云模型重建的方法。特征点能够更好地代表人脸曲面特征变化,其选择的准确性直接影响三维人脸点云模型重建的精确度,大量的伪特征点会增加计算量,并导致重建后的人脸失真。因此为避免伪特征点的干扰,本文采用动态特征矩阵求解法完成粗配准,然后采用二次加权法向量垂直距离法精确地选择人脸流形表面更有效的特征点,并基于特征融合与局部特征一致性约束的迭代最近点方法实现精配准。通过减少伪特征点的数量,降低伪特征点对配准精度和效率的影响,从而实现高精度且快速的三维人脸点云模型重建。
1 算法整体设计
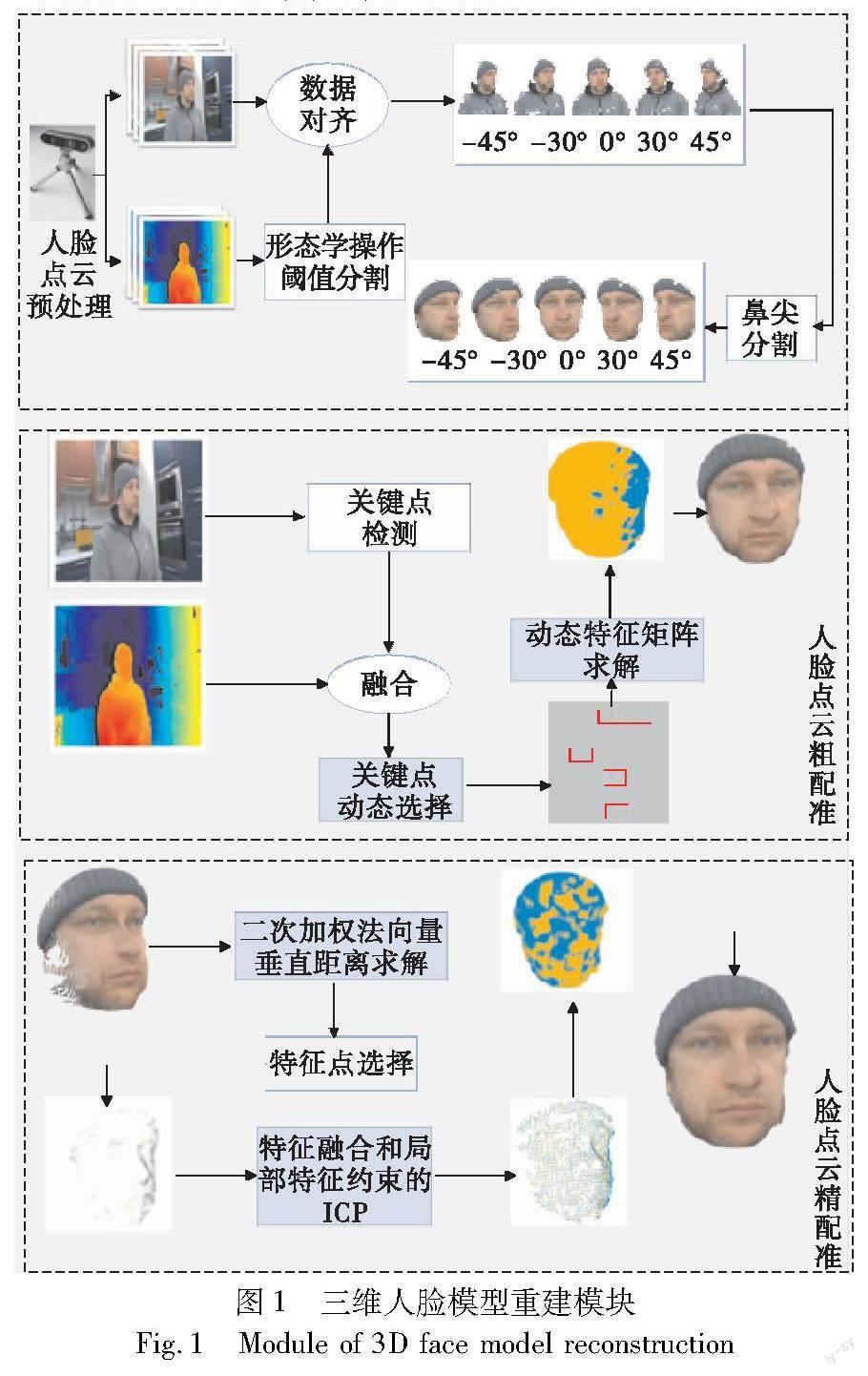
基于多视角RGB-D的三维人脸点云模型重建主要包括粗配准和精配准两个过程。为解决现有方法中伪特征点过多导致配准效率低和配准结果不精确的问题,提出了一种基于特征点动态选择的三维人脸点云模型重建的方法(DSFP),整体模块如图1所示。首先,对数据进行预处理,采用形态学操作、阈值分割和鼻尖点分割法,分割出人脸区域。接下来,采用动态特征矩阵求解法动态选择部分人脸关键点,通过多次迭代获取最优点以求解初始特征矩阵,有效避免伪特征点的干扰,实现较高精度且较快的粗配准,为精配准提供良好的初始位姿。然后,在精配准阶段,提出二次加权法向量垂直距离法来精确提取人脸流形表面更有效的三维特征点,通过减少伪特征点的数量,降低伪特征点对精配准的影响,在保证配准精度的同时,提高配准效率。为了弥补三维特征点提取过程中部分特征点丢失和存在误匹配点对的问题,采用基于特征融合与局部特征一致性的迭代最近点方法,将二维特征关键点和三维特征点深度融合,同时利用颜色一致性约束进行局部交叉验证,实现高精度且快速的三维人脸点云模型重建。
2 人脸点云粗配准
针对传统的粗配准算法因伪特征点过多导致配准效率低和冗余计算的问题,提出了基于动态特征矩阵求解(DFMS)的人脸点云粗配准方法。DFMS能够避免伪特征点的干扰,同时保证粗配准的精度、减少计算量、提高配准效率,为后续的ICP精配准算法提供良好的初始位置,避免其在迭代过程中陷入局部最优。
2.1 人脸关键点检测
首先,采用梯度提升决策树算法检测人脸二维关键点;然后创建一个与原始彩色图像相同大小的掩膜mask,将人脸关键点对应的目标区域的像素值设置为白色,非关键点区域设置为黑色;接着,将原始彩色图像与掩膜mask进行按位与操作,以提取出人脸关键点;最后结合对应的深度信息,将其映射到世界坐标系中。该过程如图2所示。
设二维关键点集为H∈{h1,h2,…,hn},对应的深度信息为Fdepth,生成的三维空间关键点集为O∈{o1,o2,…,on}。
O∈{o1,o2,…,on}=fgbdt(H;Fdepth)(1)
其中:fgbdt代表基于梯度提升决策树算法检测的人脸二维关键点结合深度信息生成的三维关键点。基于深度信息映射为三维空间关键点集,其本质是坐标系的转换,即像素坐标系转换为世界坐标系,变换的约束条件是相机内参。
根据小孔成像原理,世界坐标系中的点[xw,yw,zw]T转换为像素坐标系中的点[u,v]T,其变换公式如下:
zcuv1=fx0cx0fycy001RT01xwywzw1(2)
则像素坐标系中的点[u,v]T映射为世界坐标系中的点[xw,yw,zw]T。
xw = zc×(u-u0)×dxfyw =zc×(v-v0)×dyfzw=zc(3)
其中:fx、fy、cx、cy的单位为像素;(fx,fy)为相机焦距;(cx,cy)及(u0,v0)均为深度相机的光学中心。
2.2 基于动态特征矩阵求解的人脸点云粗配准
为避免传统的粗配准算法因人脸伪特征点过多导致配准效率低和冗余计算的问题,提出动态特征矩阵求解法求解粗配准初始变换矩阵。DFMS动态地选择人脸关键点,通过对关键点集多次迭代得到最优点集,其中每次选择的关键点数量可以不同,构造并求解动态协方差矩阵,最后选择配准点对集最小平均绝对误差对应的变换矩阵作为粗配准最终的输出初始变换矩阵。
设粗配准的源点云和目标点云的关键点集分别为Euclid Math OnePApEuclid Math OneCAp、Euclid Math OneQApEuclid Math OneCAp,动态源点集和目标点集分别为pc、qc(pc∈Euclid Math OnePApEuclid Math OneCAp、qc∈Euclid Math OneQApEuclid Math OneCAp)。求解粗配准的输出变换矩阵T0的步骤如下:
a)计算粗配准源关键点集和目标关键点集的质心和。
=1n∑Ni=1pci(4)
=1n∑Ni=1qci(5)
其中:pci和qci分别表示粗配准的动态源点集和目标点集中的第i点;n表示点集中点的数量。
b)计算协方差矩阵H。
H=1n∑Ni=1(pci-)T(qci-)T(6)
c)分解协方差矩阵奇异值,得到旋转矩阵R0及平移向量t0。
H=UΣVT(7)
R0=VUT(8)
t0=-R01n∑Ni=1pci(9)
其中:U和V分别是矩阵H的左奇异向量和右奇异向量;Σ是奇异值矩阵。
d)求解初始变换矩阵T0。
T0=R0t001(10)
e)计算该变换下的平均绝对误差E_error。
E_error=1n∑Ni=1pciT0-qci(11)
循环上述步骤,直至达到循环次数阈值停止迭代,选择配准点对集最小平均绝对误差对应的变换矩阵作为粗配准最终的初始变换矩阵T0的输出。
多角度人脸点云基于DFMS粗配准的结果如图3所示。
3 人脸点云精配准
基于DFMS粗配准获取初始变换矩阵对源人脸点云进行变换计算使其具有良好的初始位姿,然而未进行处理的人脸点云仍可能存在密度不均匀和伪特征点过多的问题。此外,标准ICP算法因全部点云参与迭代,相邻点的局部特征差异较小,对过量的伪特征点进行特征提取和特征匹配会导致收敛速度慢,并产生大量的误匹配结果,最终导致人脸点云配准失败。
3.1 基于二次加权法向量垂直距离的人脸三维特征点提取
为解决未进行处理的人脸点云仍可能存在密度不均匀和伪特征点过多的问题,首先对人脸点云进行滤波预处理,以去除噪声点并降低点云复杂度。接着,结合混合搜索算法(RKNN),提出基于二次加权法向量垂直距离法,以进一步筛选局部空间几何变化明显,且位于重合区域内概率较大的有效三维特征点。通过减少伪特征点的数量,保证配准的精度,同时减少计算量。
3.1.1 点云滤波
1)统计滤波
统计滤波[14]是一种基于统计学理论的点云滤波方法,用于去除点云中的离群点和噪声。通过计算点云中每个点的邻域点的统计属性,如平均值、标准差等,来判断该点是否为离群点或噪声,并进行相应的滤波处理。本文首先对每个点的邻域进行统计分析,设点云中的第n点坐标为Euclid Math OnePApn(Xn,Yn,Zn) ,则该点到任一点Euclid Math OnePApm(Xm,Ym,Zm)的距离为
Si=(Xn-Xm)2+(Yn-Ym)2+(Zn-Zm)2(12)
计算遍历每点到任意点之间距离的平均值和标准差:
μ=1n∑ni=1Si(13)
σ=1n∑ni=1(Si-μ)2(14)
设标准差倍数为std,算法实现过程中仅需输入k和std两个阈值,当某点的k个临近点的平均距离在标准范围(μ-σ×std,μ+σ×std)内时,保留该点,不在该范围内则定义离群点剔除。
2)体素滤波
经统计滤波处理后的人脸点云仍存在数据量庞大的问题,本文结合体素滤波下采样点云,降低点云复杂度,同时保留人脸几何特征。体素滤波是一种点云降采样技术,通过将点云空间划分为一系列体素,对于每个体素计算其中所有中心点坐标,然后将所有中心点作为新的稀疏点云,以减少点云数据量和噪声。
3.1.2 特征点选择
经点云滤波预处理后的人脸点云降低了复杂度,并有效地保留了人脸特征,但仍存在部分伪特征点,影响配准效率和重建精度。因此,本文提出二次加权法向量垂直距离法,进一步提取人脸流形表面局部空间几何变化明显且位于重合区域内概率较大的三维特征点。设经点云滤波得到的人脸点云为Euclid Math OnePApEuclid Math OneCAp′,Euclid Math OnePApEuclid Math OneCAp′中的任一点pi二次加权法向量垂直距离的均值Di为
Di=1k∑kj=1e-dij×e-dic(15)
其中:dij是利用RKNN算法得到的k個和查询中心点距离小于给定半径的近邻点到局部平面Ωp的中心点pi法向量的均值垂直距离,也代表点pi处的曲面变化程度;dic是任一点pi到点云质心pc的距离。局部平面Ωp可以通过基于局部拟合的法向量估计求得:
Ωp(n,d)=argmin(n,d)∑ki=1(n×pi-d)2(16)
dij=1k∑ki=1|pij-pi|(17)
其中:n为平面的法向量;d为到坐标原点的距离;e-dij作为权重函数,用于增加偏远邻近点的比重,易于关键点的筛选。然后再利用特征值分解求解点云质心pc并求解dic, e-dic作为二次权重函数用于进一步筛选出位于重合区域内概率较大的三维特征点,如式(19)所示。
pc=1k ∑ki=1pij(18)
dic=1n∑ni=1|pi-pc| 0≤i≤n(19)
然后利用求得的二次加权法向量垂直距离Di,提出了精确关键点选择的约束条件,设Euclid Math OnePApEuclid Math OneFAp为基于二次加权法向量垂直距离法提取的三维人脸关键点集。
Euclid Math OnePApEuclid Math OneFAp∈{pcf1,pcf2,…,pcfn} if Di>ε(20)
其中:ε为设定的阈值参数。当Di小于阈值ε,剔除该点;反之,则保留该点作为关键点。经二次加权法向量垂直距离法提取的人脸三维特征点如图4所示。
3.2 基于特征融合与局部特征一致性约束的ICP精配准
为解决在提取人脸三维特征点集的过程中可能存在特征点信息丢失的问题,进一步将人脸的二维关键点和三维特征点融合,构建精配准的人脸初始点集。然而,精配准的源初始点集和目标初始点集仍可能存在部分误匹配的点对,因此,通过结合K最近邻快速搜索,提出基于颜色一致性约束的局部交叉验证方法来剔除誤匹配点对,增加特征匹配的准确性,实现最终的最优变换关系估计。
3.2.1 人脸特征融合
为了弥补在提取三维特征点过程中可能存在的特征点信息丢失,通过融合人脸二维关键点补充人脸特征信息,构造精配准点集。设人脸二维和三维特征点融合后的源特征点集和目标特征点集分别为Euclid Math OnePApEuclid Math OneFAp_f和Euclid Math OneQApEuclid Math OneFAp_f。
Euclid Math OnePApEuclid Math OneFAp_f=PF+PC(21)
Euclid Math OneQApEuclid Math OneFAp_f=QF+QC(22)
3.2.2 初始点对集求解
将人脸特征融合后的源点云和目标点云的三维特征点集作为精配准的基础点集,根据每个点的FPFH特征,结合K最近邻快速搜索源特征点云距离目标特征点云的最近点,计算每个点到最近邻点的欧氏距离,并构造对应点对的人脸初始点对集合,设人脸初始点对集为Euclid Math OnePApEuclid Math OneQAp{Euclid Math OneFAp_init 。对于每个源特征点集Euclid Math OnePApEuclid Math OneFAp_f中的点pfi,其在目标点云Euclid Math OneQApEuclid Math OneFApEuclid Math OneFAp_f找到它最近的点qfj,即
qfj=argminqcfk dist(pfi,qfk)(23)
其中:dist(pfi,qfk)为(pfi,qfk)之间的距离度量。本文采用欧氏距离作为度量方式,则人脸点云初始点对集合为
Euclid Math OnePApEuclid Math OneQApEuclid Math OneFAp_init={(pfi,qfj)|pfi∈Euclid Math OnePApEuclid Math OneFAp_f,qfj∈Euclid Math OneQApEuclid Math OneFAp_f}(24)
3.2.3 误匹配点对剔除
针对K最近邻得到的关键点对集PQEuclid Math OneFAp_init仍可能存在误匹配点对,影响人脸点云模型重建结果的问题,本文提出基于颜色一致性约束的局部交叉验证方法剔除误匹配点对,可获得更精确的关键匹配点对,进而提高重建精度。假设对于初始点对集Euclid Math OnePApEuclid Math OneQApEuclid Math OneFAp_init,它们分别包含n和m点,源特征点云Euclid Math OnePApEuclid Math OneFAp_f中的点pfi颜色为pci,目标特征点云Euclid Math OneQApEuclid Math OneFAp_f中点qfj颜色为qcj,本文基于颜色一致性保留颜色标签相同的对应点对,剔除伪特征点对。
Cd=argmincd∑ni=1minmj=1‖pci-qcj‖2(25)
Euclid Math OnePApEuclid Math OneQApEuclid Math OneFApC={(pfi,qfk)|Cd<δ}(26)
其中:‖pci-qcj‖2表示点pfi对应的颜色pci与点qfj对应的颜色qcj之间欧氏距离的平方;设置阈值δ,保留小于该阈值的点对;Euclid Math OnePApEuclid Math OneQApEuclid Math OneFApC表示保留所有源特征点云Euclid Math OnePApEuclid Math OneFAp_f 和目标特征点云Euclid Math OneQApEuclid Math OneFAp_f中颜色标签相同的点对,即{(pfi,qfk)}。
基于颜色一致性约束剔除部分错误点对后,可能存在源特征点云中多个点的最近邻点对应目标特征点云中的同一点qfj,本文提出基于局部交叉验证,进一步剔除存在歧义的误匹配点对,只保留一对对应点。假设源特征点云中点pfi的最近邻点为目标特征点云中的点qfj,源特征点云中点pfk也与qfj匹配,其中i≠k。如果pfi与 qfj的欧氏距离小于pfk与qfj距离,则将pfk与qfj的匹配剔除。
具体地,设dist(pfi,qfj)表示点pfi和qfj之间的欧氏距离,dist(pfk,qfj)表示点pfk和qfj之间的距离,则使用式(27)剔除多余的点对。
(i,j)∈M(k,j)∈Mdist(pfi,qfj)≤dist(pfk,qfj)(i,j) keptdist(pfi,qfj)>dist(pfk,qfj)(i,j)removed(27)
其中:M表示匹配对应关系集合;(i,j)表示源点云中的点pfi与目标点云中的点qfj匹配。如果(i,j)被保留,则将(k,j)从M中移除;如果(i,j)被剔除,则将(i,j)从M中移除。最后,M中剩下的匹配对应关系即为保留下来的对应点对。
3.2.4 最优变换关系估计
基于特征融合与局部颜色一致性约束获取最终参与精配准的点对集,采用ICP点云配准算法实现人脸点云精配准。设最终参与精配准的点对集为Euclid Math OnePApEuclid Math OneQApfiner,作为ICP算法的初始输入,通过对应关系计算源点云和目标点云之间的旋转矩阵R与平移向量构成的变换矩阵T,将源点云中的所有点pfi通过变换矩阵T进行变换,得到更新的点云,直到目标函数式(28)收斂,进而完成人脸精配准。
E(R,t)=argmin(R,t)1n∑ni=1(R×pfi)+t-qf 2j(28)
其中:点pfi与qfj是对应的匹配点对。
4 实验结果与分析
4.1 数据集及评价指标
为了验证实验,本文选用两个RGB-D人脸数据集进行测试。英特尔D435深度相机采集的连续多帧多角度的人物数据集,包含107帧彩色图像和对应的深度图像,图像分辨率为1 280×720。Biwi Kinect Head Pose Database数据集[15]采用Kinect深度相机采集的24个男性和女性的RGB-D图像,分辨率为640×480。
三维人脸点云模型重建的结果采用均方根误差、平均绝对误差以及XYZ各轴方向的旋转误差5个指标来衡量。
a)均方根误差(RMSE),用于衡量测量值和真实值之间的偏差。
RMSE=∑ni=1(Xi-X^i)2n(29)
其中:n为对应点对的数量;Xi为配准后对应点之间的欧氏距离;X^i为对应点之间欧氏距离的真值。
b)平均绝对误差(MAE),可以更好地反映预测值误差的实际情况。
MAE=1n∑ni=1|Xi-X^i|(30)
c)XYZ三轴方向的旋转误差,用于判断配准后和真值间的旋转误差。其中,Ti,j代表变换矩阵T的第i行第j列的元素。
Rx_error=arccos((T1,1+T2,2)/2)(31)
Ry_error=arccos((T0,0+T2,2)/2)(32)
Rz_error=arccos((T0,0+T1,1)/2)(33)
4.2 数据预处理
针对英特尔D435深度相机采集的连续多角度的人物数据集进行实验,为了获取较为干净的深度图像和点云数据,对彩色图像和深度图像进行预处理,整体的处理流程如图5所示。首先,采用形态学操作和阈值分割去除复杂背景,以获取较为干净的深度图像,再将彩色图像和深度图像进行数据对齐生成点云,最后基于鼻尖分割获取人脸点云数据。
因人物每个视角数据都存在部分缺失点云(图6),所以需要将各个角度的人脸点云进行配准。根据经验,本文选择了五个角度的人脸数据作为算法的输入,这五个角度分别是-45°、-30°、0°、30°、45°。这样的选择在数据分布上是均匀的,并且包含了完整的人脸信息。为了确定最佳的测试数据数量,进行可靠性考量实验,在实验中,分别选取RGBD-Integration-2020数据集中的3张、5张以及7张多角度人脸数据,并使用文献[7~9]以及DSFP算法进行测试。基于DSFP算法的实验结果如表1所示。根据表1中的结果得出结论:选择5张多角度人脸数据进行三维人脸点云模型重建是最优的。因此,本文选择-45°、-30°、0°、30°、45°五个角度的人脸数据作为后续消融实验和对比实验的基础测试集。
4.3 消融实验
4.3.1 基于动态特征矩阵的消融实验
为了验证动态特征矩阵求解实现粗配准的有效性,进行了相关消融实验,相关实验结果如表2所示,并将结果可视化,如图7所示。由图7结果发现,传统基于几何特征进行的粗配准效果较差,本文提出的动态特征矩阵求解法在粗配准过程中动态选择部分人脸关键点,通过对关键点集多次迭代得到最优点集,避免伪特征点的干扰,实现粗配准变换矩阵的动态求解。其中RMSE达到了2.687 3 mm,仅用时6.275 8 s,相比其他算法,配准精度分别提高了59.155%、65.974%、69.065%,在保证配准精度的同时,减少了计算量。
4.3.2 基于二次加权法向量间垂直距离的消融实验
为证明提出的二次加权法向量垂直距离法(QWNVD)提取人脸流形表面三维特征点的有效性,进行了相关消融实验,实验结果如表3所示。
分析表3的结果可以发现,基于QWNVD的重建结果优于文献[9]等算法。另外,由于在粗配准过程中通过DFMS动态选择关键点求解粗配准初始变换矩阵,使得结合了DFMS和QWNVD算法的重建效果优于QWNVD等其他算法,仅用时6.785 7 s便实现了三维人脸重建,各轴方向的旋转误差也低于其他算法,RMSE相比其他算法分别下降了42.581%、35.599%、29.546%、17.239%,在保证配准精度的同时,减少了计算量。
4.3.3 基于局部特征一致性约束与特征融合的ICP消融实验
基于特征融合与局部特征一致性约束的ICP相关消融实验的结果如表4所示。其中DFMM和QWMM分别表示CFICP融合了DFMS和QWNVD的算法。由于DFMS在粗匹配過程中动态选取关键点进行动态特征矩阵求解和QWNVD提取有效关键点的优势,使得基于特征融合与局部特征一致性约束的ICP在DFMS和QWNVD的基础上实现了良好的重建性能,整体上优于列举的对比算法。DSFP算法实现三维人脸重建仅用时6.875 0 s,MAE 达到了2.410 8,RMSE相比其他算法分别下降了35.856%、41.046%、8.9565%、7.656%、2.705%,同时提高了配准效率。
4.4 对比实验
本文算法是在自带NVIDIA GeForce RTX 3060显卡的Windows 11系统上实现的,基于数据集RGBD-Integration-2020中的-45°、-30°、0°、30°、45°五个角度的人脸RGB-D数据与ISS-ICP [7]、ANGLE-ICP [8]、FPFH-ICP [9]等算法进行重建对比测试,重建结果如表5所示,并将重建结果可视化,如表6所示。
表5报告了基于数据集RGBD-Integration-2020的对比实验的结果。本文DSFP算法得益于DFMS、QWNVD和CFICP的优势,在性能上优于其他算法,三维人脸点云模型重建仅耗时6.875 0 s,RMSE达到了1.816 5 mm。DSFP算法的重建时间比文献[7]多花费了
0.184 3 s,可能的原因是ISS-ICP仅在粗配准过程中采用ISS提取特征点,直接采用传统ICP算法进行精配准,减少了数据融合和误匹配点对剔除的时间,但是重建时间相较于ANGLE-ICP、FPFH-ICP算法,分别减少了9.622 5 s、5.926 3 s。DSFP算法的RMSE性能相较于其他算法,分别下降了40.101%、47.724%、53.150%,各方向上的旋转误差也远小于其他算法。DSFP算法在保证配准精度的同时,减少了计算量,验证了其有效性。
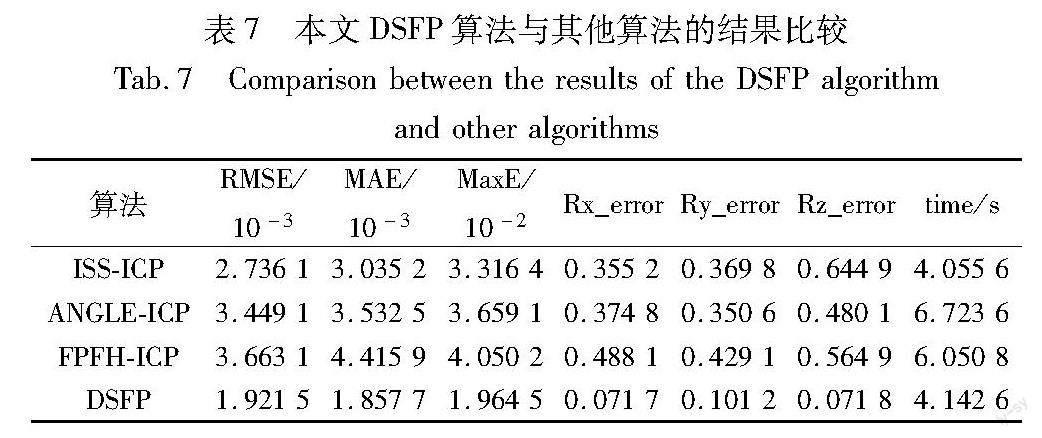
为了进一步验证本文DSFP算法的优越性,基于数据集Biwi Kinect Head Pose Database[15]进行相关对比实验,结果如表7所示。表7报告了基于该数据集的对比实验结果,可以看出本文DSFP算法在该数据集上也有很好的应用效果。在精度上明显高于经典的ISS-ICP、ANGLE-ICP和FPFH-ICP算法,各方向上的旋转误差基本可以忽略,配准RMSE较ISS-ICP算法减少了30.101%,较ANGLE-ICP降低了约44.290%,较FPFH-ICP降低了47.538%,重建时间相较于ANGLE-ICP、FPFH-ICP算法分别降低了2.581 0 s和1.908 2 s。
5 结束语
本文提出了一种基于特征点动态选择的三维人脸点云模型重建方法,可以根据不同的人脸图像进行自适应处理。通过在二维和三维空间进行特征点有效提取并采用动态选择策略,有效减少了伪特征点的数量,从而降低伪特征点对重建效率和精度的影响,避免了因伪特征点过多导致的人脸点云模型重建失真的问题。为了验证本文DSFP算法的有效性,进行了相关消融实验和对比实验, RMSE达到了1.816 5 mm,与其他算法相比,其RMSE分别降低了40.101%、47.724%、53.150%。实验结果证明,DSFP算法能够实现高精度且快速的三维人脸点云模型重建,具有良好的应用前景。下一步,将致力于研究人体全身三维模型的重建。
参考文献:
[1]Liu Feng, Zhao Qijun, Liu Xiaoming, et al. Joint face alignment and 3D face reconstruction with application to face recognition[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2020,42(3): 664-678.
[2]Khan K, Ali J, Ahmad K, et al. 3D head pose estimation through facial features and deep convolutional neural networks[J]. CMC-Computers, Materials & Continua, 2021,66(2): 1757-1770.
[3]Mao Xiaoyan, Li Xiaojian, Jia J, et al. Validity and reliability of three-dimensional costal cartilage imaging for donor-site assessment and clinical application in microtia reconstruction patients: a prospective study of 22 cases[J]. Clinical Otolaryngology, 2020,45(2): 204-210.
[4]Tran L, Liu Xiaoming. On learning 3D face morphable model from in-the-wild images[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2019,43(1): 157-171.
[5]Feng Yao, Feng Haiwen, Black M J, et al. Learning an animatable detailed 3D face model from in-the-wild images[J]. ACM Trans on Graphics, 2021,40(4): article No.88.
[6]Besl P J, McKay N D. A method for registration of 3D shapes[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 1992,14(2): 239-256.
[7]黃际玮, 陆安江. 基于特征点与改进ICP的点云配准方法[J]. 微处理机, 2022,43(6): 38-42. (Huang Jiwei, Lu Anjiang. A method of point cloud registration based on feature points and improved ICP[J]. Microprocessors, 2022,43(6): 38-42.)
[8]单丽杰, 岳建平, 钱炜. 基于特征点的ICP点云配准算法[J]. 甘肃科学学报, 2022,34(4): 1-4,19. (Shan Lijie, Yue Jianping, Qian Wei. ICP point cloud registration algorithm based on feature points[J]. Journal of Gansu Sciences, 2022,34(4): 1-4,19.)
[9]张泽鹏, 赫森奥, 张明哲, 等. 基于FPFH-ICP的三维工件点云配准方法研究[J]. 信息与电脑: 理论版, 2022, 34(13): 54-57. (Zhang Zepeng, He Senao, Zhang Mingzhe, et al. Research on 3D artifact point cloud registration method based on FPFH-ICP[J]. Information & Computer: Theory, 2022,34(13): 54-57.)
[10]Ahuja Y, Nitharwal T, Sundriyal U, et al. Depth reconstruction based visual SLAM using ORB feature extraction[J]. Journal of Image and Graphics, 2022,10(4): 172-177.
[11]Jung S, Song S, Chang M, et al. Range image registration based on 2D synthetic images[J]. Computer-Aided Design, 2018,94(12): 16-27.
[12]Zhe Ji, Fan Zhou, Xiang Tian, et al. Probabilistic 3D ICP algorithm based on ORB feature[C]//Proc of the 3rd International Conference on Information Science and Technology. Piscataway, NJ: IEEE Press, 2013: 300-304.
[13]Choi S, Zhou Q Y, Koltun V. Robust reconstruction of indoor scenes[C]//Proc of IEEE Conference on Computer Vision and Pattern Re-cognition. Piscataway, NJ: IEEE Press, 2015: 5556-5565.
[14]Rusu R B, Marton Z C, Blodow N, et al. Towards 3D point cloud based object maps for household environments[J]. Robotics and Autonomous Systems, 2008,56(11): 927-941.
[15]Fanelli G, Dantone M, Gall J, et al. Random forests for real time 3D face analysis[J]. International Journal of Computer Vision, 2013,101(3): 437-458.

