突发性公共事件下应急物资分级协同配送研究

柳虎威, 周 丽, 杨江龙

(北京物资学院信息学院，北京 101149)

0 引言

突发性公共卫生事件越来越多地引起社会各界的关注，尤其是“新型冠状病毒”的肺炎疫情爆发以来，其超强的传染性导致数以万计的人感染，世界卫生组织宣布，疫情构成全球突发公共卫生事件。随着疫情的不断发展，受灾严重地区出现医疗物资严重不足，居民的生活物资紧缺等现象。因此，如何将应急物资及时、高效地调度到受灾区域已成为广泛关注的焦点问题，这也是应急物资管理一个重点研究问题。

突发事件的频繁发生，推动了应急物流的发展，而应急物资调度是应急物流的一个重要环节。应急物流具有突发性、急迫性、特定性、缺乏计划性、作业量不均衡等特点。当突发事件出现时，需要在短时间内将应急物资调配到灾区，降低损失。多仓库应急物资分级协同配送，能够合理调度应急物资，实现各部门协同配合，快速、精准调拨分配应急物资，以最快的速度提供援助，尽快做出救援响应，使得各项救援工作能快速、有序、高效展开，并能保障各环节无缝连接。在出现异常时快速反应、及时调整，合理调配有限的物流资源，实现救灾效果最大化目标，提高整体的救援效率，保证应急物流系统稳定性。因此，研究多仓库应急物资分级协同配送具有重要意义。

针对应急物资配送问题，考虑将应急物资按照重要程度分级，并在多仓库间实现协同配送，从而构建了应急物资分级协同配送模型，并在改进LSTM 网络的基础上结合遗传算法的理论框架，设计了针对该模型的求解算法。最后，进行模型算例仿真，验证模型的有效性，为应急物资配送活动提供一定的参考和借鉴。

应急物流是应对突发事件的非常态物流，重大灾害事件的发生，推动了应急物流研究的发展。应急物流领域的相关研究主要包括应急物资分级管理、应急物资协同配送以及应急物资的储运协同等方面。

在应急物资分级管理方面，丁斌和王鹏[1]通过建立应急物资模糊综合评价模型，结合层次聚类方法对数据分析，确定不同种类应急物资的储备模式；Ruan 等[2]考虑了在灾害应对中，应急决策者通常会考虑多个因素向紧急分配点分配救援物资，提出一种比较三角模糊数的新方法；Afshar 和Haghani[3]提出建立综合物流模型应对自然灾害，通过供应链从货源中获得救济品并送到接受者手上，该模型不仅考虑了诸如车辆路径和取货或交货等细节时间表，也考虑仓库和运输系统的容量限制；Akbarpour 等[4]针对药品项目综合救灾网络设计问题，提出的双目标模型考虑了药品的易腐性、救济的移动性设施，并针对需求不确定性，研究了模型的鲁棒性。

在应急物资协同配送方面，王妍妍和孙佰清[5]以物资短缺的延迟损失最小化与物资分配的总成本最小化为目标构建考虑多集散点、多配送中心和多受灾点的三级配送网络的应急物资动态多阶段分配模型，并设计了目标转化与线性近似相结合的模型求解方法；冯春等[6]在考虑应急物资分类与分批配送的基础上，建立了效率目标与公平目标相结合的多周期应急物资分批配送模型，并设计了针对多目标优化模型求解Pareto 解集算法；陈业华和马晓玉[7]以串联式需求系统修复的时间最短及成本最小为目标，分别构建了纵向配送的应急物资调度模型和纵向配送与横向转运相结合的应急物资协同调度模型，并通过遗传算法对两种模型进行求解；朱佳翔等[8]针对应急物资配送过程中救灾信息具有鲁棒不确定性特点，构建应急物资配送多阶段多目标鲁棒优化模型，研究了外部不确定输入扰动和内部不确定性扰动的情况；王海军等[9]考虑模糊需求下应急物资的需求分配与网络配流问题，建立了以最小总配送时间为目标的网络流模型，设计了基于双边约束的重力模型算法和凸组合算法；Sakiani 等[10]提出的特定库存路径模型体现了救济品分配的公平性，并采用模拟退火算法进行计算，使再分配能显著提高救灾行动的绩效；Davis 等[11]提出了协作仓库网络中定位和分布的随机规划模型，以便更有效地预先安排供应，为其在业务层面的分配做好准备；Najafi 等[12]提出了一个多目标、多模式、多商品、多周期的物流管理随机模型，根据层次目标函数设计求解算法，并应用于救灾物资的分配过程中；Dou 等[13]针对应急物资协同调配效率低下的现实问题，分析了影响效率提高的关键因素，通过研究表明决策者的协调能力和信息传递效率是影响效率的重要因素；D’Uffizi 等[14]使用离散事件模拟作为决策支持，规划适用于紧急情况和风险情况的行动，仿真结果表明，在紧急情况下能够有效地分配不同的资源，并选择特定时间内可用的最佳解决方案；Chen 等[15]提出了疫情演化与资源需求预测模型，通过模型可以估计不同的演化阶段以及每个阶段所需的医疗资源；Wang 等[16]提出了应急物资调运模型，针对物资运输多目标、时间最短、成本最小进行优化，并对理想点算法结合蚁群算法进行比较，通过实验验证了模型和算法的合理性。另在应急物资储运协同方面，近年来相关研究乏善可陈。

综上所述，在应急物流方面，主要分析应急物流的特点类型，为应急物流系统的配送研究奠定基础；在应急物资分级管理方面，通过建立不同的应急物资评价模型，确定不同种类应急物资的管理方式，运用不同的数据分析方法，有层次聚类方法、Vague 集和信息熵、动力演化算法等；在应急物资协同配送方面，依据物资需求、时间、成本、物资库存以及应急物资的分类等情况，构建配送模型并运用目标转化与线性近似相结合的方法、遗传算法、重力模型算法、凸组合算法、蚁群算法和径向基神经网络结合的方法以及模拟退火算法等求解模型；在应急物资储运协同方面，主要包括建立储运管理信息网络体系，构建储运安全管理运行机制的建构，以及国家、行业、企业多层面协同运作等内容。

故本文以物资分级和协同运输为研究视角，充分考虑突发公共事件下对不同重要程度的物资进行分级，为节约运力最大程度地减少运输距离，在优先配送重要物资的前提下，构建多种物资协同配送模型，丰富了突发公共事件下物资配送的研究内容。在模型求解方面，基于进化机制和神经网络结构设计了LSTM-GA 算法，以GA 的进化机制辅助LSTM 网络迭代寻优。这一算法改进了传统优化算法侧重优化具体方案的特点，主要针对神经网络构成的策略机制进行优化，使得该算法更能适应动态变化的问题特性和前提条件，并能在神经网络端到端的作用机制下实时做出动作决策。

1 应急物资分级配送模型假设

关于不同类型的公共事件，比如由传染性疾病引发的公共卫生事件、由自然灾害引发的公共突发事件、由暴力冲突引发的公共安全事件等。不同类型的公共事件下应急物资的分级与协同配送是不同的。例如，突发公共卫生事件下医药物资和防护物资的重要级别高于其他物资，自然灾害引发的公共事件下急救物资和生活必须品的重要级别高于其他物资，自然灾害及其它突发公共安全事件下协同配送很可能由于交通堵塞导致物资难以运抵目标地点。故在仿真分析中加入了对不同物资种类情况的讨论，论证模型的适用性。

所谓应急物资的分级，是指根据突发公共事件下的应急需求，对各类物资的供应进行轻重缓急的区分。如突发公共卫生事件下医疗物资的重要的程度最高，其次是生活必须品，再次是普通生活用品。如果是突发传染性疾病，那么医疗物资中的防护用品和急救药物的重要级别更高，而治疗其他普通病症的药物则重要程度相对较低。在供应各类物资时，将其进行不同重要等级的划分，有利于合理利用有限的运输力量，有限满足重大且急需的社会需求。

假设突发事件爆发区域内，需要配送的应急物资按照重要程度分为n个级别(1 为最高，n为最低)，存在m个仓库，且区域内物资供需状态St，随着配送活动的进行而不断变化。在初始状态S0下，第i个仓库warehousei各类物资的存储量可分别表示为：，则在系统状态为St时，所有仓库各类物资的储量可用矩阵Ot表示如下

其中i=1,2,···,m,j=1,2,···,n,t ≥0 且为整数。∑

设第k个需求点中第j类物资完成配送的时间为Tkj，Tmax 为整个区域的全部配送过程结束时，最后一次针对某需求点某类物资的配送任务完成时间。当供不应求时，即所有仓库应急物资已配送完，但仍有需求点存在尚未满足的需求，则将相应尚未满足需求的需求点中，相应种类物资配送完成时间设为：2·Tmax。另设变量Tsum 记录整个系统状态变化经历的总时间，由于配送活动和时间的变化成正比，假设运输车辆形式单位距离耗费1 个单位的时间成本，则将配送距离与配送时间等同考虑。

设共有g辆运输车负责整个区域的配送任务，每辆车的最大载重量为Gmax，所有车辆均可混合装载不同类别的物资，并且可将各不同仓库的物资，在整个区域范围内配送到所有需求点。第h辆运输车vehicleh在系统状态为St时，装载第j级物资的重量为Gthj，则有

所有运输车辆系统状态为St时，载重量情况可以表示为矩阵Gt，则有

其中h=1,2,···,g，各运输车辆初始状态S0的装载量为0，即G0hj=0。

此外，仓库与仓库之间，需求点与需求点之间，以及仓库与需求点之间的距离可表示为矩阵D，则有

2 应急物资分级配送模型构建

由于是分级配送应急物资，应尽量保证重要程度较高的物资优先得到配送，并且用尽可能短的时间完成所有物资的配送。换句话说，要构建的模型应使重要物资的配送时间尽可能短，且总配送时间也尽可能短，这样获得的收益越大。因此，本研究考虑将配送时间最小化的研究思路，转换为总收益最大化的角度进行分析，构建如下目标函数

其中重要级别系数Pj−1远远大于Pj，Pj远远大于Pj+1，即P1≫P2≫···≫Pj ≫···≫Pm。

另外，整个区域内的应急物资是多仓库分级协同配送，可以看作贯序决策过程。通过进一步分析可知，决策系统不同状态的信息及其状态转移规则，并需要将不同状态下的决策原则与决策空间进行说明。

对于整个区域内，多仓库应急物资分级协同配送系统的状态信息包括：

1) 不同状态下各仓库的物资存储信息为Ot；

2) 各需求点对不同类别物资的需求信息，即为Qt；

3) 当前状态，各运输车辆混合装载各类物资的数量，即为Gt；

4) 所有仓库和需求点两两之间的距离信息，即为D；

应急物资分级协同配送的系统状态信息，可以用集合St表示如下

应急物资多仓库分级协同配送系统，不同状态下的决策以及状态转移规则如下：

4) 通过车辆不断将仓库存储的货物运输到各需求点，直至所有仓库的存储量均为0，即

或者所有需求点的需求量全部满足，即

时，整个配送过程结束。

整个区域内，应急物资多仓库分级协同配送的具体贯序决策过程如下：

1) 确定系统的初始状态。初始状态Tsum=0，所有仓库物资存储量为初始值，所有需求点的需求量为初始情况，所有车辆当前载重为0，所有车辆当前所处的位置为其所在的仓库，要前往的下一结点也初步设置为所在仓库本身，则所有车辆到下一个结点的距离为0，系统整体的初始状态可表示为S0={O0,Q0,G0,D,E0}；

2) 对所有仓储的所有运输车辆，装载当前该最重要的物资，直至每辆车装载数量为Gmax 使其达到满载，或仓库的物资全部装载完毕，则停止装载活动。对当前装载量大于0 的所有车辆进行配送任务指派，指明各自的目标需求地。此时更新系统状态信息，由于本研究仅考虑货物配送所耗费的时间，暂时忽略货物装载时间，因此Tsum 并未发生变化，仍然为0，但仓库的当前存储量，运输车当前载重量，运输车下一目标结点，以及距离下一目标结点的距离均已发生变化，系统状态更新为S1={O1,Q1,G1,D,E1}；

3) 确定E1中，最小的distance ari1h值累加到Tsum 值上，令其他的distanceari1h值减去这一最小值，将这一最小值对应的运输车辆物资类型和载重量与相应的目前需求点信息进行对照，同时更新车辆载重信息和目标需求点的需求信息，然后更新系统状态为S2={O2,Q2,G2,D,E2}；

通过以上对于突发事件区域内应急物资配送过程分析，建立应急物资多仓库分级协同配送的贯序决策模型，针对该模型需进一步设计算法进行求解。

3 分级协同配送模型算法设计

本研究根据应急物资多仓库分级协同配送过程的特点可知，任一车辆在任一装载和配送过程中的微小变化，都会对其他车辆的装载和配送产生重要影响。因此，通过改进人工智能算法中的LSTM 网络，并将其与遗传算法的理论框架相结合，设计了求解该问题针对性更强的LSTM-GA 算法。

在该算法的具体设计过程中，将LSTM 网络的输入与输出结构进行改进，使其允许输入数据的维度不断变化，且输出数据的维度能够根据输入数据维度的不同相应变化。因此，在时序决策过程中，每个决策步骤所针对的状态集合的元素个数是可变的，增加了决策状态信息的丰富性，使本算法可以解决更为复杂的时序决策问题，并且较好地解决了时序决策过程中已选项重复出现的问题，一定程度上代替了指针网络的时序决策机制，具体算法过程如图1 所示。

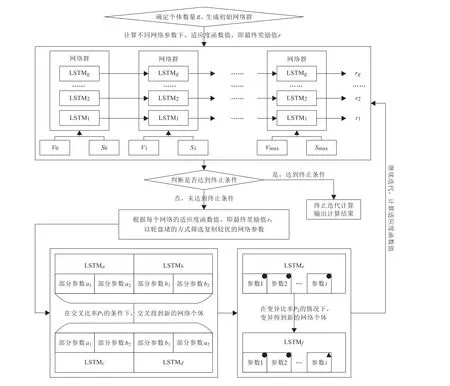
图1 LSTM-GA 算法示意图

基于改进LSTM 网络与遗传算法相结合的算法求解步骤如下：

1) 确定个体数量，生成初始的LSTM 网络群，用于时序决策过程中分别对分级协同配送车辆进行任务指派，计算不同网络参数下的适应度函数值，即奖励值r；

2) 本模型针对的节点及其之间的距离，并非采用坐标形式计算出直线距离，而是采用实际距离矩阵的方式进行表示。因此，采用V1到Vm+e表示每个节点的位置特征，具体内容为每个节点到其他节点以及其他节点到该节点的距离向量，即距离矩阵D的一行一列的信息放到一起组合成一个节点的位置特征向量；

3) 根据系统状态St(t=0,1,2,···)，判断LSTM 网络的输入。将向量V0到Vm+e分别与系统状态信息St一起合并输入网络。此处由于改进了LSTM 网络结构，能够在不同情况下依次为车辆指派下一个目标节点，直至整个过程结束；

4) 时序决策过程中下一动作的做出，即为当前distance ari 为0 的车辆指派下一目标节点，需要根据当前网络状态，输入不同规模的向量信息，根据改进的LSTM 网络输出，决定当前应采取的具体动作；

6) 结合遗传算法框架，针对适应度函数值采用轮盘赌的方式，进行网络参数复制，并按照一定的交叉率和变异率对群体中的网络参数进行交叉和变异操作，从而得到新的网络群体，然后进行迭代计算，直至达到预先设定的终止条件，停止计算并输出最终结果。

4 分级协同配送模型算例仿真

采用随机生成方式，获得算例数据。将算例规模设置为3 个仓库，3 类物资，20 个需求点，5 辆运输车，每辆最大载重10 单位，车辆初始位置随机分布于各个仓库。由于供需不相等的运输配送问题，可以较为容易地转换为供需相等的问题，所以只考虑供需相等的情况。采用实际距离的方式表示各节点间的距离，随机生成各节点间的距离矩阵和车辆的初始位置信息。设定任意两节点间的距离服从1 到10 的均匀分布，即D～U(1,10)，任意需求点的初始需求量服从1 到5 的均匀分布，即Q0～U(1,5)。由于物资是分级配送，且第1 类物资的重要程度远远大于第2 类物资，第2 类物资的重要程度远远大于第3 类物资，因此优先运送高一级重要程度的物资。

运用Python 语言编程，改进LSTM 网络并与遗传算法结合。其中，改进LSTM 网络的参数Hidden Size 设为64，NumLayers 设为4。另外，根据本算例的具体情况，将奖励值函数设为r= 1−(Tsum/300)。由于本算法采用遗传算法的框架对改进的LSTM 网络参数进行优化，可以通过数值实验的方式确定初始网络群中的网络个数以及交叉变异率，如图2 和图3 所示。在数值实验的过程中，分别将网络群体中的个体数量设置为10、20、30、40 和50，将交叉率与变异率设为相等(统称为交叉变异率)，且均从0.05 开始以步长为0.05 的方式递增，增至上限0.95 时停止。同时，将不同个体数量下适应度函数值的均方差，以及不同交叉变异率下的适应度函数均值，分别作为个体数量与交叉变异率的寻优程度指标。由图2 可知，个体数量为20 个时，即可达到较高的优化程度；由图3 可知，交叉变异率越高，则响应的适应度函数值优化程度越高，但要防止当群体个数较少且交叉变异率较高时，迭代计算时无法保留上一次迭代的最优网络。因此，综合上述因素并结合实验数据，将个体数量参数设为20，交叉变异率设为0.8。

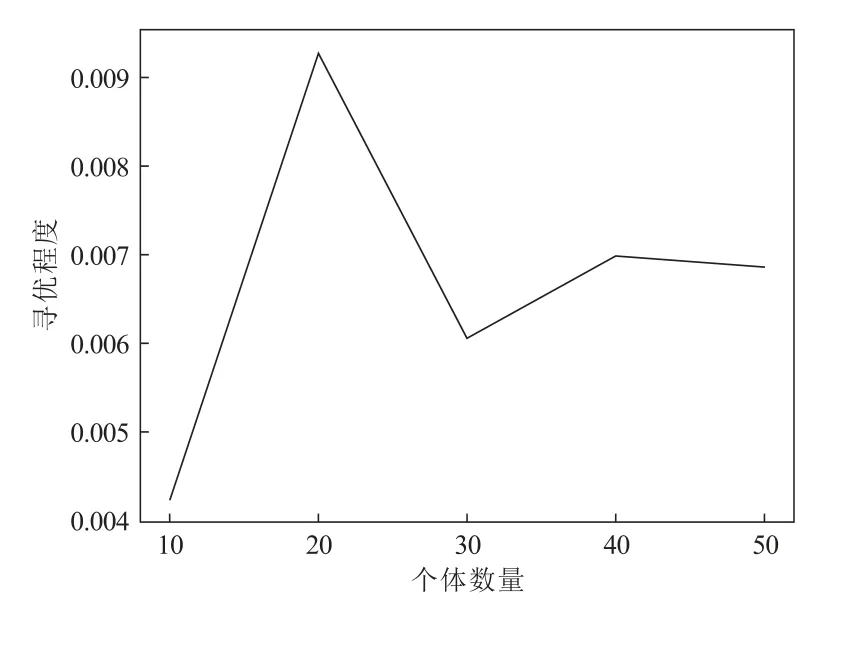
图2 不同个体数量下的寻优程度

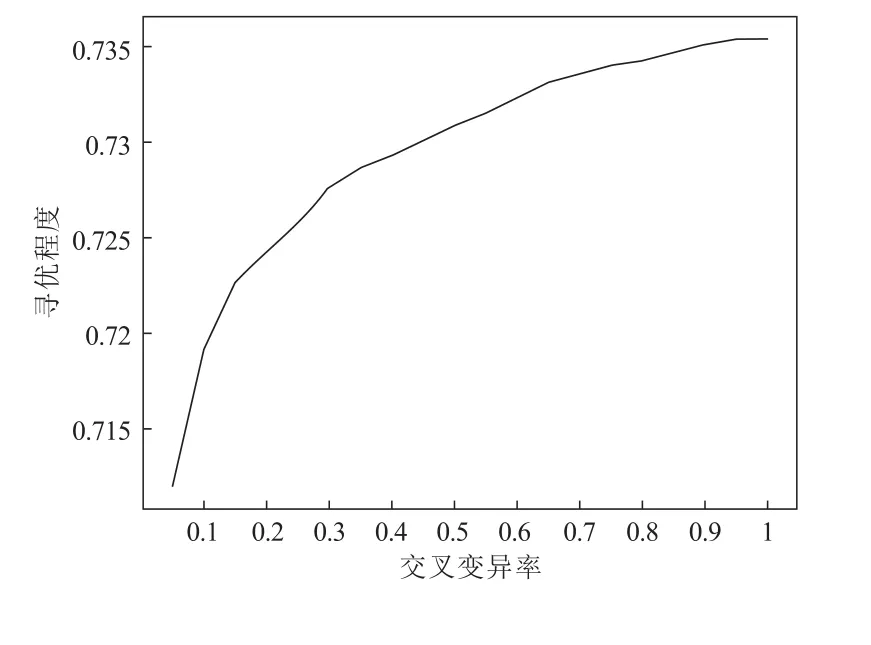
图3 不同交叉变异率下的寻优程度

根据设定好的各项参数指标，进行算例模拟。为了使求解结果达到较高的优化程度，将最大迭代次数设定为100 次，得到的算例结果如图4 和图5 所示。其中，图4 显示在使用改进的LSTM 网络与遗传算法的理论框架结合后，所设计的算法使求解过程具有较快的收敛速度，且收敛过程更加稳定。根据应急物资分级协同配送模型的求解结果，可以到整个区域内各仓库与需求点之间具体的协同配送方案，如图5 所示。在图5 中，方框代表仓库，其编号为0 至2；圆圈代表需求点，其编号为3 至22；箭线代表车辆行驶路线，箭线上的数字代表车辆编号，其编号为0 至4。根据计算结果，可以得到时序决策过程中，每次决策的细节信息，包括分级协同配送过程中，每辆运输车每次到达哪个仓库或需求点，分别装载或卸载各种应急物资的数量等，为整个区域内应急物资的调配提供切实可行的优化方案。

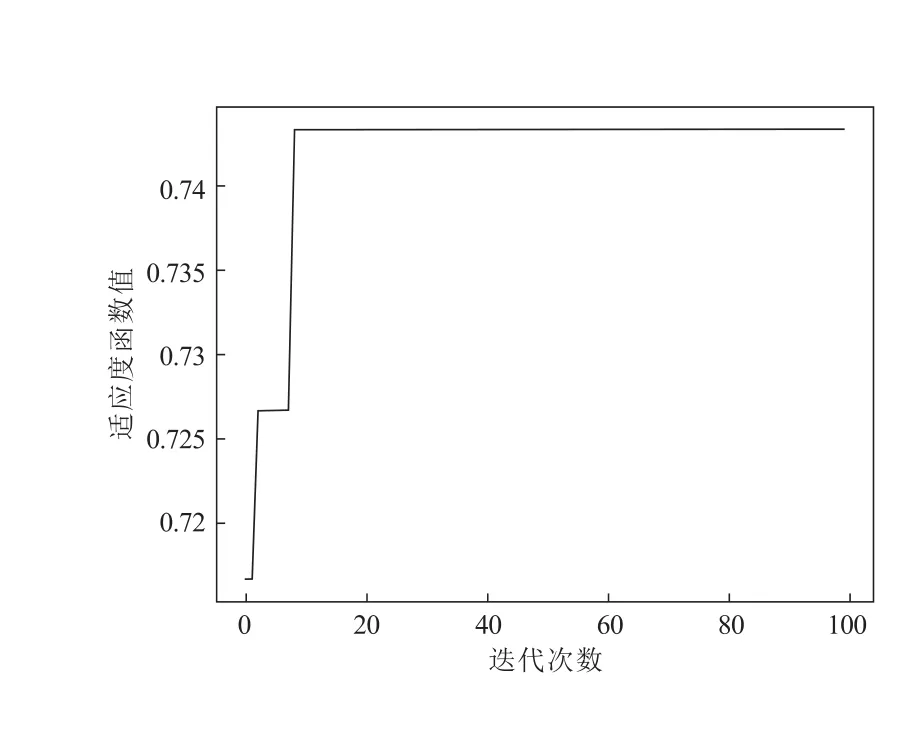
图4 算例迭代计算适应度函数值

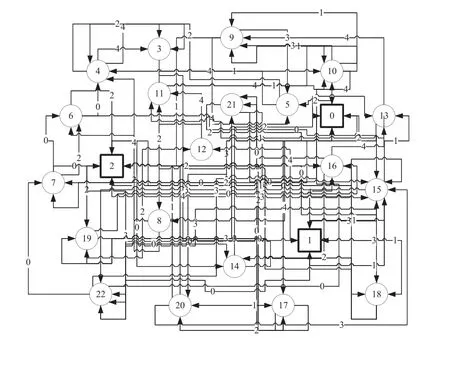
图5 协同配送算例仿真路线示意图

为了进一步深入研究不同情况下的物资调配情况，将影响物资调配方案的各种约束条件进行分类。主要分为相对固定的优化条件(短期内不易改变)与动态变化的优化条件(短期内可以改变)。其中，相对固定的优化条件包括：仓库数量、需求点数量、运输车最大载重量、节点距离；动态变化的优化条件包括：物资种类、运输车数量、需求点需求量。

将前面的基础算例作为算例1，并将其作为参照算例。本文中将相对固定的优化条件的取值和算例1 相同，短期内可出现较大变化的动态条件分别设置较多和较少两种情况。如表1 所示，物资种类较少的情况为3 种，较多的情况为9 种；运输车辆较少的情况为5 辆，较多的情况为10 辆；需求点的需求量较少的情况服从1～5 的均匀分布，较多的情况服从5～10 的均匀分布。

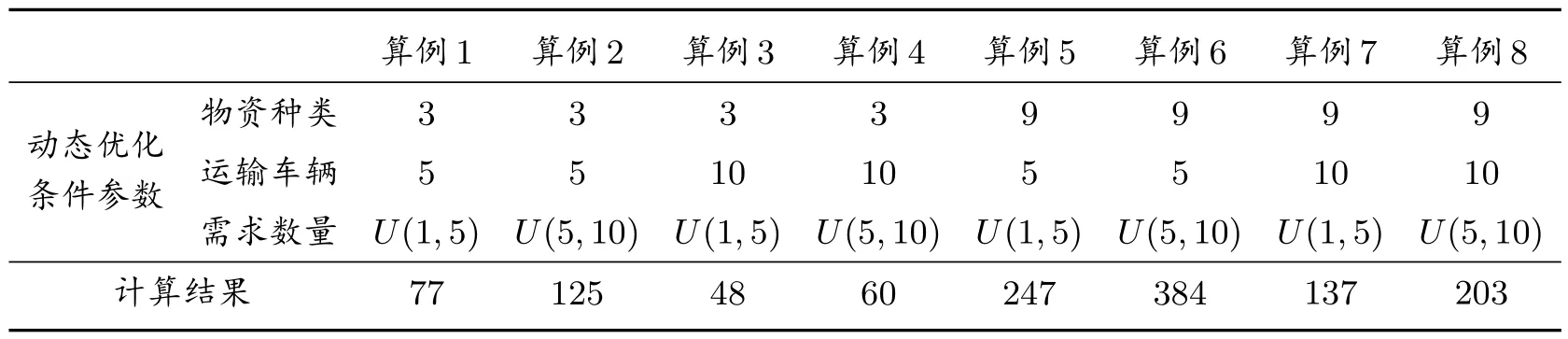
表1 不同动态优化条件的参数设置和算例结果

参照前面基础算例(即算例1)的算法超参数取值，得到算例2 至算例8 的计算结果，如表1 所示。各算例的计算迭代过程，如图6 所示。

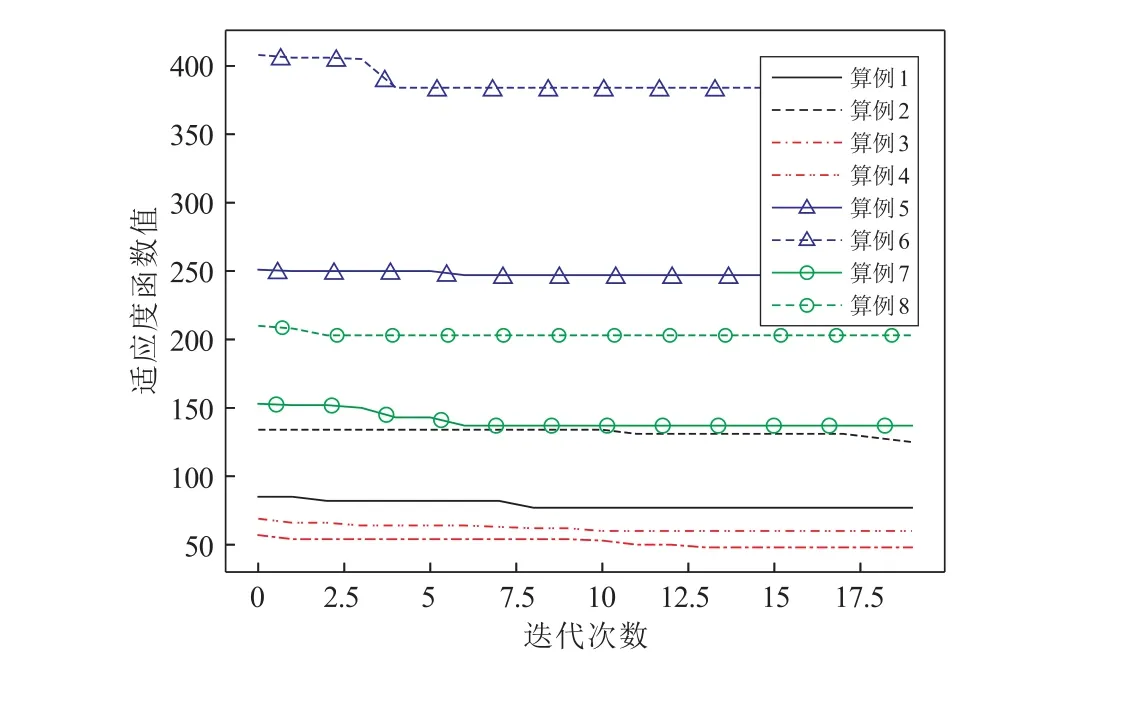
图6 动态优化条件不同参数设定算例结果对比

进一步对比分析不同算例之间计算结果的差异，将三种动态条件中的两种条件相同且第三种条件不同的情况进行划分，如表2 所示。其中，针对物资种类、运输车辆和需求数量的情况1 至情况4 具体内容不同，例如，针对物资种类这一动态条件，情况1 是指运输车辆较少且需求量较少的情况；针对运输车辆这一动态条件，情况1 则是指物资种类较少且需求数量较少的情况，其他情况具体见表2。

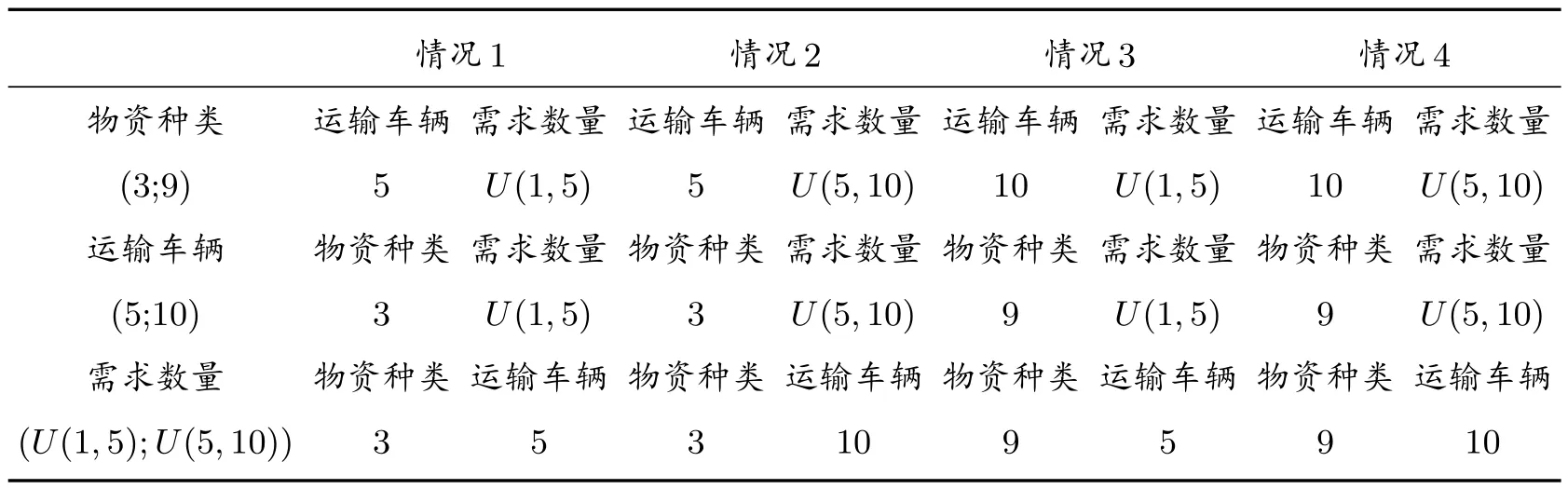
表2 两种动态条件相同一种不同的情况划分

在表2 不同类型的4 种情况基础上，分别对比不同情况下每种动态条件变化的结果增减比例程度，如表3 所示。由表3 可知，针对物资种类变化的情况3，当运输车辆较多且每个需求点需求量较少时，物资种类的增加导致运输距离的增加程度明显小于其他情况下的物资种类增加；针对运输车辆变化的情况2，当物资种类较少且需求点需求量较多时，车辆数量的增加导致运输距离减少的程度明显高于其他情况下运输车辆增加的影响；针对需求点需求数量变化的情况2，当物资种类较少且运输车辆较多时，需求数量的增加导致运输距离的增长幅度最小。

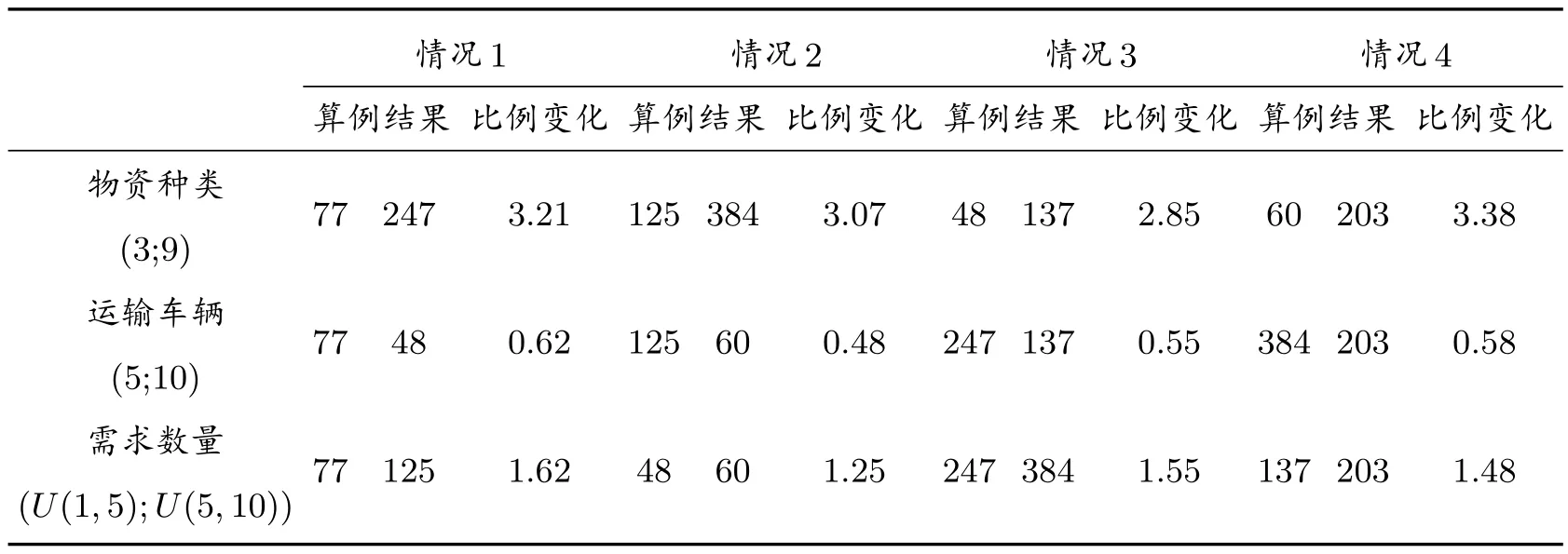
表3 不同情况动态条件下的算例结果变化

5 结论

针对突发性公共事件导致的应急物资调配问题，本文在综述前人相关研究的基础上，将研究的关键点聚焦于应急物资的分级协同配送，并建立时序决策模型，设计了改进LSTM 网络与遗传算法框架结合的求解算，并进行算例模拟验证了算法的有效性。具体内容主要包括以下几个方面：

1) 前人在研究物资调配的问题时，较少考虑物资的分级问题，但是面对不同类型的具体公共突发事件，应急物资的重要程度是不同的。因此，在本文的研究中，将应急物资按照重要程度进行了分级，并设定了优先运送重要物资的原则；

2) 关于协同配送的问题，由于企业各自为政的现象较为普遍。因此，在普通物资的流通领域并不常见，但在应急物流领域这样的特殊情况，协同配送是建立应急物资统一供应体系的必然举措。本文针对这一问题建立了协同配送模型，使运输车辆及各类应急物资，能在整个区域内进行整合优化；

3) 在模型构建方面，将协同配送与时序决策结合起来，将多辆运输车之间的协同配送，转换为时序决策的模型，这样以来降低了多智能主体多任务指派问题的计算复杂程度，使得在大规模问题的情况下，针对时序决策模型的算法依然能够适用；

4) 在算法设计方面，本研究改进了LSTM 网络结构，结合该网络结构设置了状态生成、状态转移及奖励值计算函数，实现了LSTM 网络接收和输出信息维度的可变性，并将该网络与遗传算法框架相结合，使LSTM-GA 算法的收敛速度与稳定性得到改进，一定程度上拓展了LSTM 网络的适用范围。