铝/不锈钢双金属管爆炸焊接数值模拟

缪广红,马秋月,胡 昱,周大鹏,孙志皓, 刘自伟,马宏昊,沈兆武

(1.安徽理工大学 力学与光电物理学院, 安徽 淮南 232001;2.安徽理工大学 土木建筑学院, 安徽 淮南 232001;3.中煤科工集团淮北爆破技术研究院有限公司, 安徽 淮北 235000;4.中国科学技术大学 中国科学院材料力学行为和设计重点试验室, 合肥 230027)

0 引言

金属的爆炸焊接是介于金属物理学、爆炸以及焊接工艺之间的一门交叉学科,它的优点是制造大面积的任意组合、任意形状、任意尺寸和多种用途的双金属或多金属复合材料[1]。爆炸焊接除了可以进行板、板之间的焊接外,还可以进行各种金属之间的搭接焊、点焊、缝焊以及金属复合棒材、复合管等焊接。双金属爆炸焊接复合管是由2种不同材质和性能的金属管通过爆炸焊接方法复合而成,由于其兼具基管和复管材料的各自优势,因此具有广阔的应用前景[2]。爆炸焊接制备金属复合管,能够制造出耐磨损抗烧蚀的小型装甲车辆用速射炮的内膛,承压设备中输送气体的错复合管、核电用内铝-钢复合管、加速器真空箱壁用的大口径的铜-钢复合管等。且生产成本低,复合质量高,不存在焊缝和电位腐蚀,弥补了传统焊接方法的缺点。

近年来,关于金属管材的爆炸复合也有了很多实验研究。Tian等[3]采用水下爆炸焊接工艺制备了铜/钢复合管;Ren等[4]进行了不同爆炸载荷下的爆炸焊接试验,获得了30CrMnSi/钨合金复合材料棒材。张龄匀等[5]采用套娃式新型爆炸焊接法一次试验高效制备出以Q235钢为基管、T2紫铜为覆管的Q235/T2 复合管及以1060工业纯铝为覆管、T2紫铜为基棒的1060/T2复合棒各一件。邓伟等[6]通过在粉状乳化炸药中添加不同比例密度调节剂得到不同的炸药爆速,进行了铝/不锈钢复合管爆炸焊接实验,以确定该复合管合理的炸药爆速范围。但由于爆炸焊接过程具有瞬时性,直接对过程进行测试费时费力,且具有一定的危险性。而采用数值模拟的方法,不仅能直观地反映出爆炸焊接过程中基复管之间的碰撞情况,而且还能减少试验次数、有效降低成本,不失为研究爆炸焊接过程的一种行之有效的方法。

目前常用的模拟分析方法基本可分为有网格和无网格2类,如经典的网格随体坐标移动的拉格朗日法和无网格的光滑粒子流体动力学(SPH法) 等,拉格朗日法的优点在于结构划分简单,对于微小变形的问题能够提供精确的模拟结果,但当模拟对象出现大变形情况则网格较容易发生畸变导致计算无法继续进行;SPH法具有较强的自适应性,能够很好地处理不同介质的交界面并避免极度大变形导致的网格扭曲,较为适合用于求解高速冲击碰撞问题,缺点是当设置高求解精度时需要较大的计算内存且求解时间极长[7]。

本研究中主要基于 ANSYS/LS-DYNA软件,以文献[6]中的试验为基础,建立了铝/不锈钢双金属管爆炸焊接模型,分别采用SPH-FEM耦合法和拉格朗日法,对复合管爆炸焊接过程进行了分析,并研究了不同爆速下复合管的复合情况,为爆炸焊接过程中炸药爆速的合理选择提供了一种有效方法。

1 爆炸复合窗口

对于2种不同金属的爆炸焊接,通过实验和理论计算确定的爆炸焊接可焊参数的范围就称为爆炸焊接窗口[8],如图1 所示。爆炸焊接参数极限主要有:流动限、声速限、上限以及下限[9-10]。基于文献[6]中的爆炸焊接试验,本研究中爆炸焊接窗口的材料参数如表1所示。

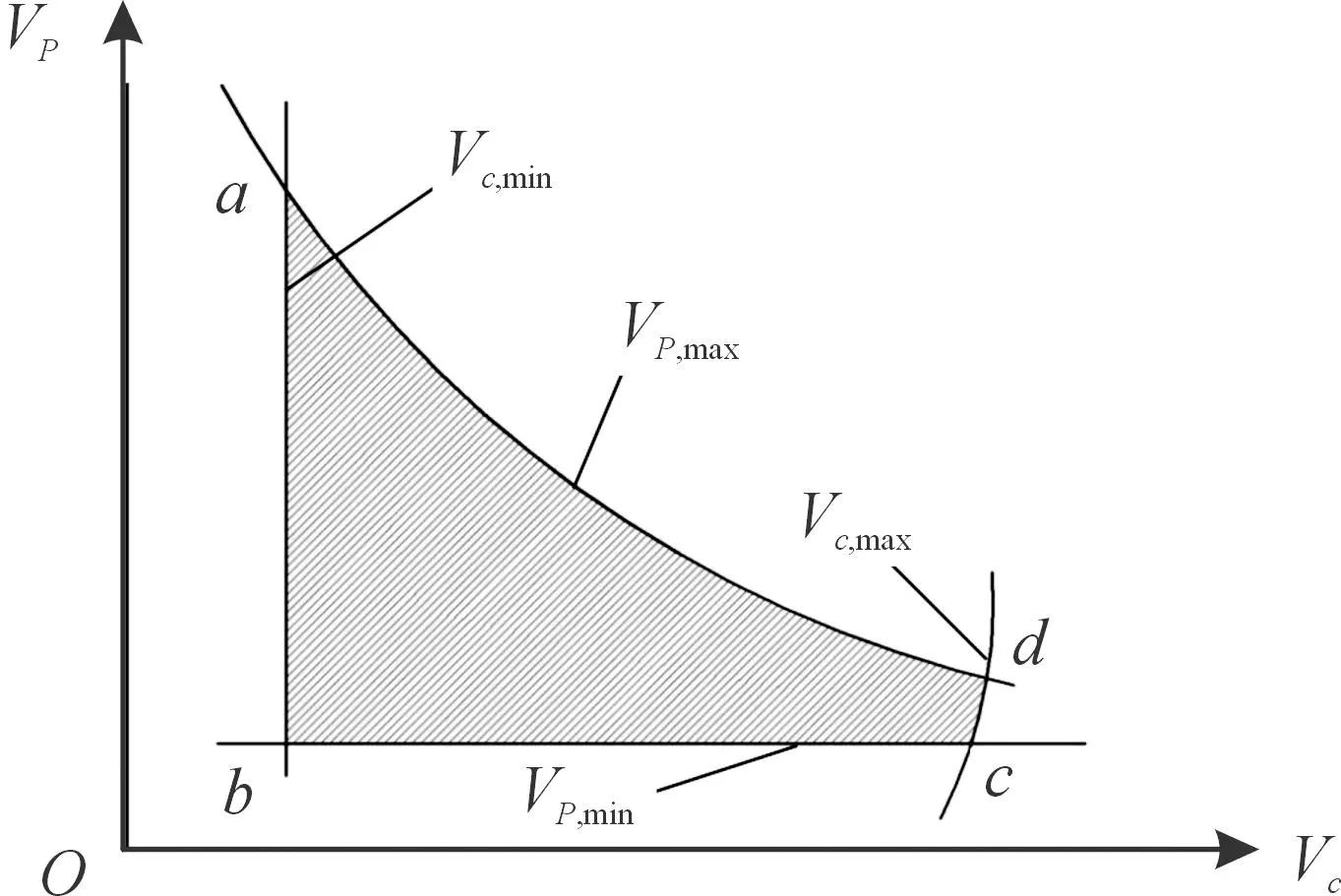
图1 爆炸焊接窗口

表1 材料参数

1.1 流动限

流动限是保证射流产生以及撞击点最小的移动速度,当撞击点移动的速度达到Vc时,金属表面开始出现射流,Vc是使待结合面产生射流的临界撞击点速度[11]当撞击点移动速度小于Vc时,碰撞点压力小于材料动态屈服极限,则不能产生射流,从而不能实现焊接。因此,撞击点移动速度应该大于临界撞击点移动速度Vc[8]。临界撞击点移动速度Vc,min,采用Erza提出的公式:

(1)

式(1)中:σ为基复板中较高一方的屈服强度,MPa;ρ为基复板中较小一方的密度,g/cm3;结合表1中的参数可得,撞击点最小的移动速度为:Vc,min=1 881 m/s。 在平行法爆炸焊接中,碰撞点的移动速度即为炸药的爆速[12],所以炸药的爆速应大于1 881 m/s。

1.2 声速限

爆炸焊接的声速限是为了保证形成射流,而对基复板最大碰撞速度做出的限制。一般来说,碰撞点的移动速度必须小于材料的声速,才有可能形成射流,因此双金属爆炸的声速限公式为[13]:

Vc,max=C0min

(2)

式(2)中:C0min为基复板2种材料中声速的最小值;由式(2)求得Vc,max=4 569 m/s,平行法爆炸焊接中碰撞点移动速度应等于炸药爆速,即炸药的爆速应小于4 569 m/s。

1.3 下限

爆炸焊接下限是对爆炸焊接最小能量的限制,也是射流形成的条件[14]。复板相对基板的碰撞速度要达到一定程度,形成的高压才能使基复板间产生射流。复板与基板最小的撞击速度叫做爆炸焊接的下限,单金属爆炸焊接下限Vp,min可由以下经验公式[8]求得:

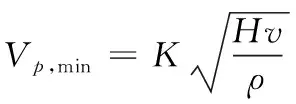
(3)

式(3)中:Hv为材料的维氏硬度;K为常数,取0.6;该公式作为单金属射流形成条件是比较准确的,但公式中只有一种金属的性能参数,对于双金属爆炸焊接来说不够准确[15]。双金属爆炸焊接需要使2种材料中较硬的材料产生塑性变形。所以在计算双金属爆炸焊接下限时,可以先利用式(3)分别计算出基复板2种金属能够产生射流的最小碰撞速度Vp,min,然后再分别计算出2种金属的最小可焊压力Pmin1、Pmin2为:

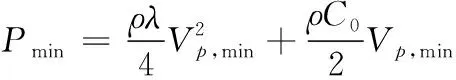
(4)

式(4)中:C0为材料声速;λ为材料的线性系数;取两者最大值作为双金属的最小可焊压力,表示为:

Pmin=Max(Pmin1,Pmin2)

(5)

再分解求出2种金属的碰撞速度u1、u2为:

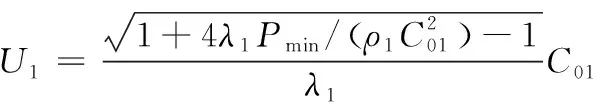
(6)

(7)

可求得最小碰撞速度为:

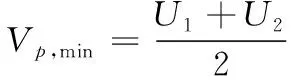
(8)

可以计算出碰撞速度下限Vp,min=491.69 m/s,即复板的碰撞速度必须大于491.69 m/s。

1.4 上限

爆炸焊接常被归类为固相焊[11]。复板与基板撞击速度太大,将导致结合界面产生熔化。因此在进行金属板爆炸焊接时,界面熔化可能导致在结合界处产生脆性金属间化合物,损害界面结合强度。为了避免界面出现熔化,复板和基板最大撞击速度Vp,max,可用以下经验公式[11]确定:

(9)

式(9)中:ρ1、ρ1分别为复板和基板的密度,g/cm3;CP1、CP2分别为复板和基板的比热,J/(kg·k);α1、α2分别为复板和基板的热扩散率,m2/s;Tmp min为复板和基板两者中熔点较低值,K;C01、C01分别为复板和基板的声速,m/s;N为理论常数,一般取0.039;tmin为反射稀疏波达到界面的最短时间,s;tmin=min(2d1/C01,2d2/C02);Vc为碰撞点的移动速度,m/s;通过计算可以得到Vp,max=1 041 m/s,即复板的碰撞速度必须小于1 041 m/s。

2 计算模型及参数选取

2.1 计算模型

基于文献[6]的基础,选取不锈钢管(316L)为基管,纯铝管为复管。基复管间隙为1 mm,炸药为乳化炸药,起爆方式为点起爆,起爆位置为炸药端部中心。利用 LS-DYNA 软件建立爆炸焊接三维模型,基复管模型参数如表2所示。SPH-FEM耦合模型建模过程中,将炸药生成SPH光滑粒子,对基复管均采用有限元网格划分,SPH-FEM 耦合模型示意图如图2所示。拉格朗日模型建模过程中炸药与基复管材料均选用3D Solid164 实体单元,采用更为精准的六面体映射网格对整体进行划分,拉格朗日模型示意图如图3所示。计算中忽略空气作用,考虑到模型的对称性,为了提高计算效率,只取1/4模型进行计算,模型中单位制为cm-g-μs,于模型整体的X、Y边界加设对称边界条件,基管外表面施加位移约束。

表2 基复管模型参数

图2 SPH-FEM 耦合模型示意图

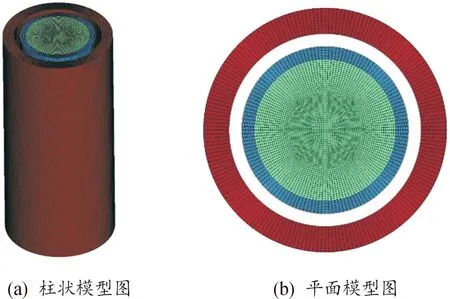
图3 拉格朗日模型示意图

2.2 参数选取

2种算法在计算过程中各材料的模型参数选取一致,炸药采用高能燃烧模型和 JWL状态方程[16-18],JWL状态方程的表达式为:

(10)

式(10)中:A、B、R1、R2和ω为材料参数;P为爆轰产物压力(GPa);E0为初始比内能(GPa);V为爆轰气体产物的体积比(常数);乳化炸药的JWL状态参数见表3所示。

表3 乳化炸药的JWL状态参数

在数值计算时,基、复板均采用Mie-Gruneisen状态方程和Johnson-Cook材料模型[19]Johnson-Cook 材料模型的形式为:

(11)

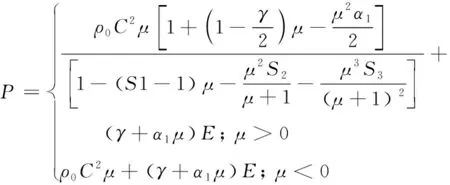
(12)

式(12)中:μ=ρ/ρ0-1;E为金属材料的内能;γ为Gruneisen常数;ρ0为材料密度;α1为对γ的一阶修正系数;S1、S2、S3为Vs-VP曲线的斜率系数;C为Vs-VP曲线的截距(声速);316L与1060Lv的Johnson-Cook材料模型参数和Gruneisen材料模型参数如表4和表5所示。

表4 Johnson-Cook材料模型参数

表5 Gruneisen材料模型参数

3 模拟结果分析

炸药爆炸速度是爆炸焊接的重要工艺参数,炸药爆速直接影响着金属管爆炸焊接的质量好坏[1]。试验的5种爆速下复合管内表面及剖面图如图4所示[6],Tube1表面出现了大面积破裂和损伤、Tube2表面出现部分烧伤、Tube3未发现明显缺陷但内表层附有大量爆炸产物、Tube4和Tube5试样焊接质量较好,复合连接区的焊缝完整,这表明铝/不锈钢复合管爆炸焊接的合适爆速为1 950～2 150 m/s,但爆速2 150 m/s时复合管内表面爆炸产物残留过大,影响后续使用[6]。本文中对相同条件下的金属管进行模拟来分析爆速对铝/不锈钢复合管结合质量的影响,化炸药参数如表6所示,模型A、B、C、D和E,分别对应Tube5、4、3、2和1。

图4 复合管内表面及剖面图

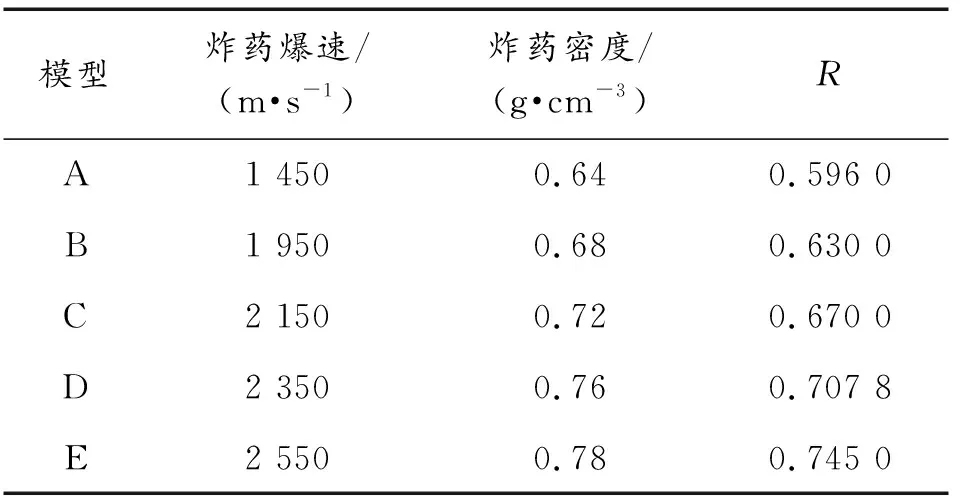
表6 乳化炸药参数

3.1 模拟过程分析

SPH-FEM 耦合算法和拉格朗日算法下,爆速为1 950 m/s,装药密度0.68 g/cm3条件下的复合管爆炸焊接过程,如图5和图6所示。模拟时,SPH-FEM 算法的耗时比拉格朗日法久。2种算法下基复管的复合情况大致相同:炸药爆炸后驱使复管均匀地向基管撞击,复管的运动碰撞状态与流体化的金属材料相似,碰撞过程中复管牢牢地结合在基管表面,没有出现拉断、碎裂、鼓包等不良现象,复合管的结合质量较好。

拉格朗日法中炸药网格在爆炸焊接过程中会产生较大程度的畸变,这是模型在计算过程中产生负体积问题的重要原因之一,严重情况下还会导致计算无法继续。而SPH-FEM 法中并不存在网格随炸药流动而变形的情况,因此能够有效避免负体积问题,并能够较为形象的模拟出炸药爆炸的飞散路径[20]。

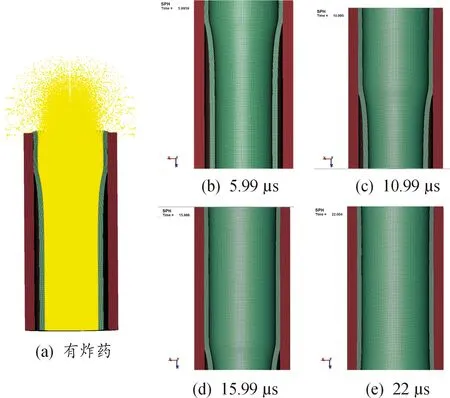
图5 SPH-FEM 耦合算法复合管爆炸焊接过程

图6 拉格朗日算法复合管爆炸焊接过程

3.2 复管碰撞速度分析

为了探究炸药爆速对复板碰撞速度的影响,在5组模型复管表面的前中后分别选取1个特征单元(Element207601、Element227901、Element246101),特征单元选取示意图如图7所示。

图7 特征单元选取示意图

并导出不同算法下的特征单元速度-时间曲线变化,如图8所示,SPH-FEM 耦合算法和拉格朗日算法下特征单元碰撞速度如表7和表8所示。复管在爆轰作用下发生变形,进而产生瞬时峰值,与基管碰撞后运动速度快速减小,呈现“几”字形。随着炸药爆速的增加,复管的碰撞速度不断增大且单元取得最大速度的加速时间逐渐缩短。

图8 不同算法下速度-时间曲线

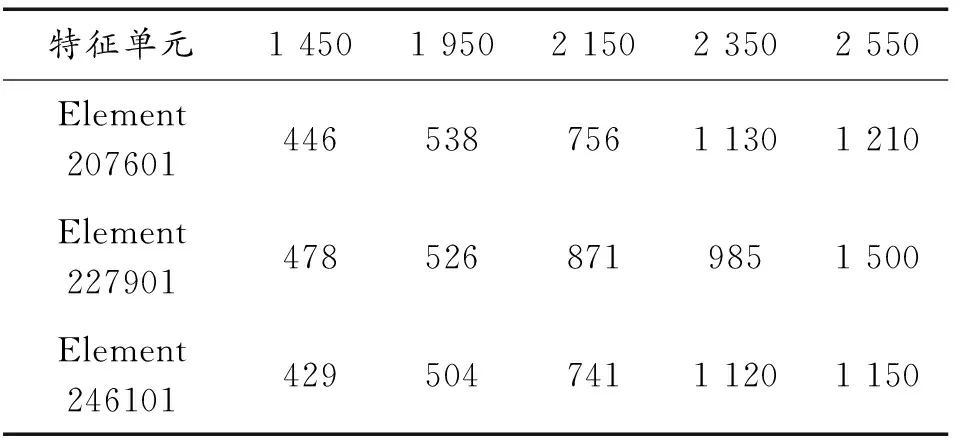
表7 SPH-FEM 耦合算法下特征单元碰撞速度

表8 拉格朗日算法下特征单元碰撞速度 Table 8 Collision velocity of feature element under lagrange algorithm (m·s-1)

结合前期计算的爆炸焊接窗口490 m/s

利用Gurney推广公式计算复管的碰撞速度:

(13)

式(13)中:R为炸药比;Vd为炸药爆速;γ为炸药的多方指数;求得炸药爆速为1 950 m/s时的复管碰撞速度为516 m/s,由SPH-FEM耦合算法计算的特征单元(Element207601、Element227901、Element246101)碰撞速度分别为538、526、504 m/s,与理论速度之间误差分别为:4.3%、1.9%、2.5%;由拉格朗日算法计算的特征单元碰撞速度分别为544、550、554 m/s,与理论速度之间误差分别为:5.4%、6.6%、7.4%。以此推断2种算法中SPH-FEM 耦合法所得的动态参数精度较拉格朗日法高。

3.3 塑性变形分析

为了更清楚地观察不同炸药爆速下复合管的结合效果,给出2种算法下20 μs时刻基复管的塑性变形云图,图9 (a)—图9 (e)分别对应模型A、B、C、D和E。2种算法下的基复管塑性变形情况大致相同:复管的塑性变形远大于基管,基管的塑形变形只发生在贴近界面的薄层中;随着炸药爆速的增加,基复管上的塑性变形也在增大。

A模型由于炸药爆速过小,塑性变形小,且主要集中在复管的起爆端,基复管结合较差。SPH-FEM 耦合算法下的D模型基复管结合处管壁出现了一处破裂,E模型基复管结合处管壁出现了多处破裂,这是由于炸药爆速较大,爆轰压力过高,碰撞速度过大,碰撞时产生的强大冲击和快速变形导致基复管来不及形变而产生了破断缺口,导致管壁出现破裂,如图9(e)所示,使得复合管质量不能满足使用的要求。因此若要获得结合质量较好的复合管,应设置炸药爆速在1 950～2 150 m/s左右,这与试验所得结论一致。

拉格朗日算法下的E模型,由于炸药爆速过大,复管变形较大,网格畸变严重,致使计算提前终止,从而无法输出20 μs时刻基复管的塑性变形云图。这表明在处理大变形的高速爆炸冲击问题时,SPH-FEM 耦合算法较拉格朗日算法更合适。

图9 塑性变形云图

4 结论

1) 利用ANSYS/LS-DYNA有限元软件结合SPH-FEM耦合法和拉格朗日法对铝/不锈钢双金属管爆炸焊接过程进行爆炸焊接模拟均是合理可靠的。

2) 炸药爆速对基复管的塑性变形和复管碰撞速度影响较大,塑性变形和复管碰撞速度过小或过大均不能实现良好结合。结合复管的最佳碰撞速度和基复管的塑性变形情况,炸药爆速为1 950～2 150 m/s左右时,基复管结合质量较好,这与试验所得结论一致。

3) 拉格朗日法建模快捷,且比SPH-FEM 算法耗时短;拉格朗日法中炸药网格在爆炸焊接过程中会产生较大程度的畸变,SPH-FEM 法中并不存在网格随炸药流动而变形的情况,且能较为形象地模拟出炸药爆炸的飞散路径。

4) 2种算法下复管特征单元的碰撞速度与理论速度之间存在1.9%～7.4%的误差。其中SPH-FEM 耦合法的误差较小,利用 SPH-FEM 耦合法能够得到最为精确动态参数。对于大变形的高速爆炸冲击问题,选择SPH-FEM耦合算法较为合适。