炮口振动特性对自动炮射击精度的影响研究

王二亮,刘 丹,王宏金,高 英,任弘毅

(西北机电工程研究所, 陕西 咸阳 712099)

0 引言

研究火炮结构振动对射击精度的影响,可以从结构层面上为火炮的射击提供良好的外弹道炮口扰动初始条件,从而提高射击精度[1]。炮口振动是影响自动炮射击精度的一个重要因素[2],在不考虑武器和弹药自身的内弹道和外弹道的设计精度影响,连发射击精度主要取决于火炮系统的安装间隙、摇架间隙、后座长度和后座轴向精度、载体和托架等刚强度等。因此通过优化火炮系统的结构设计,改善弹丸出炮口一致性,可以有效控制火炮系统的射击精度。许多科研人员考虑了身管柔性、结构非线性等因素对火炮射击时的炮口振动特性进行研究[3-6],以期提高火炮系统的射击精度。

火炮作为一个结构复杂、运动自由度多的机械系统,传统的动力学分析方法已经远不能满足对其进行振动分析的需要。随着科学技术的发展,多体动力学已成熟应用于汽车、机床、兵器等机械工程领域[7-9]。许多科研人员将火炮发射动力学与多体动力学相结合,用于研究火炮射击振动特性。王德石等[10]研究了火炮系统的冲击响应规律及固有振动特性,获得了火炮振动与其结构参数的内在联系,有效改善了火炮的振动性能。张世明等[11]建立了中口径自动炮非线性动力学有限元模型,能够有效地反应火炮射击时的振动特性,为中口径埋头弹火炮武器系统射击密集度优化提供参考。Jie等[12]分析了影响射击密集度的浮动机构参数,建立了刚柔耦合多体动力学模型,对某榴弹机枪系统的二十发射击过程进行了仿真分析。王红岩[13]则考虑了底盘振动对射击精度的影响。笔者为了进一步探究火炮结构振动对射击精度的影响,在火炮发射动力学理论的基础上,考虑自动炮各部件之间的约束关系及身管柔性,建立了刚柔耦合自动炮虚拟样机模型,并进行发射动力学仿真,初步计算了射击密集度,为自动炮优化设计提供参考依据。

1 自动炮虚拟样机建模

1.1 基本假设及系统拓扑结构分析

根据自动炮的结构特点及射击过程各部件的运动规律,在不影响模型合理性的前提下,为便于理论分析,作如下假设:

1) 除火炮身管外,炮塔及武器系统中各构件均作刚体处理;

2) 忽略车体及地面的影响,自动炮底座直接固定在台架上;

3) 考虑身管与火炮前支撑架间隙和摩擦非线性因素的影响;

4) 不考虑供输弹机构的影响,连发射击时,每发弹丸已输送到射击位置;

5) 射击时受到主动力为火药气体压力、缓冲弹簧提供的后坐阻力和复进力,不考虑自动机工作时自动机零部件间接触/碰撞的能量损耗,自动机作为后坐部分参与运动。

火炮射击时,击针击发底火后,火药气体压力推动弹丸向前运动,同时作用在炮闩底面,使自动机闩体、炮尾、身管等部件沿着摇架导轨一起后坐,同时受到缓冲弹簧阻力的作用,后坐到位后,在缓冲弹簧复进力的作用下完成复进运动。后坐力通过摇架、缓冲弹簧作用在自动炮架座上,并传给固定台架。图1为主要部件间的约束关系。

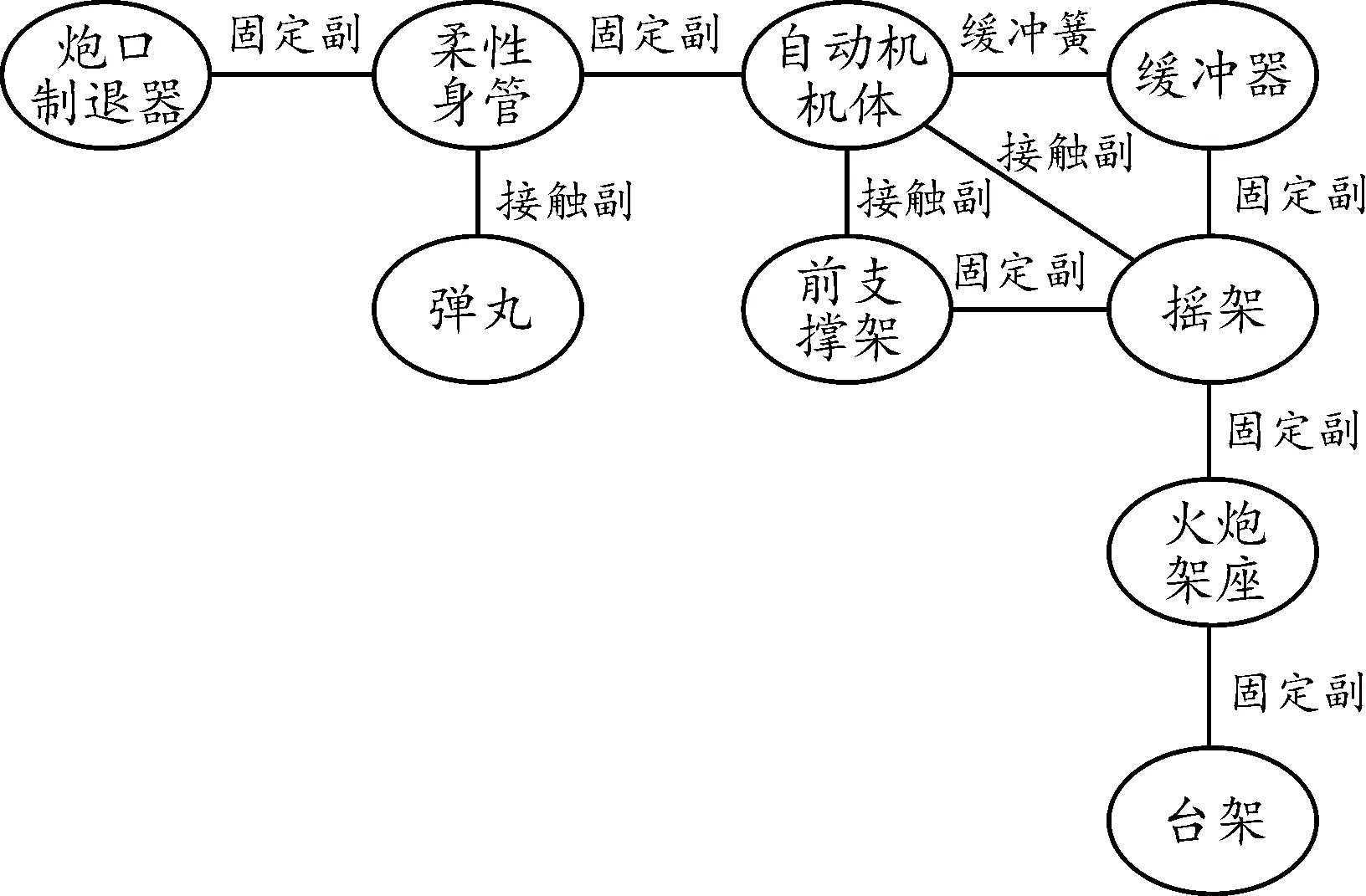
图1 自动炮主要部件间的约束关系

1.2 动力学特性仿真模型

三维实体模型的作用是为动力学分析提供各零部件的几何形状、装配关系、全炮的质量、质心位置和转动惯量等。由于自动炮系统各零部件外形比较复杂,文中利用三维建模软件建立其实体模型,将各零部件进行装配,获得装配模型,再根据系统仿真模型的约束关系,将各子部件以动力学软件能识别的格式导出,并建立动力学特性仿真模型。

根据假设,建模时将自动炮身管为柔性体。火炮射击时身管会产生较大的变形,建立柔性体模型可分析身管的弹性变形对射击精度的影响。

基于模态集成法建立身管柔性体模型。模态集成法将柔性身管看作是有限元模型的节点集合,其相对于局部坐标系有小的线性变形,局部坐标系可以有大的非线性整体平动和转动。每个节点的线性局部运动近似为模态振型或模态振型向量的线性叠加。本文中采用模态集成法在ANSYS/Workbench软件中生成零部件的柔性体中性文件流程如图2所示,图3是基于该方法建立的身管有限元模型。模型共有115 200个节点、66 569个元素,建立了6个外部节点与自动机机体和炮口制退器相连。

将身管底部、前支撑面等部位固定,分析身管在约束条件下的模态,部分频率的下振型如图4—图6所示。各阶模态信息如表1所示。

图2 运用ANSYS生成MNF文件流程图

图3 身管有限元模型

图4 第1阶模态振型

图5 第4阶模态振型

图6 第8阶模态振型

表1 身管前10阶模态信息

将建立的自动炮系统三维实体模型和身管柔性体模型导入动力学软件中,为各刚体零部件设定所用的材料属性,使其自动获得质量和转动惯量等物理信息,也可使用各零部件质量和转动惯量的测试数据,直接定义其物理属性;根据图1的系统动力学拓扑结构,定义零部件之间的运动副和运动约束。关于载荷的定义如下:

1) 自动机受到的炮膛合力通过内弹道计算得到的离散数据点,将离散数据拟合成样条曲线,以力的形式添加到自动炮后坐部分上(自动机机体尾部)。弹丸受到的弹底合力也采用同样的方法施加。

2) 在自动炮后坐部分和摇架之间添加螺旋弹簧(图7所示),设置刚度为800 N/mm,弹簧预压力为28 400 N,后坐阻尼系数40 N·s/mm,复进阻尼系数1.4 N·s/mm。

图7 缓冲弹簧添加位置

最后,根据实体模型与约束载荷等参数建立自动炮动力学特性仿真模型,如图8所示。

图8 自动炮发射动力学特性仿真模型

1.3 模型的验证

自动炮动力学仿真步长设置为一个射击循环,在实际射击过程中,后坐力是一个非常重要的参数,后坐力直接影响各个机构件的运动行程以及射击时传递的载荷大小,因此可以通过火炮水平射击时后坐和复进时后坐力及后坐位移曲线,来验证模型的准确性。模型验证以及后续计算分析的边界条件设定为:高低、方向射角0°,常温穿甲弹射击。图9和图10分别为后坐力和后坐位移的试验值和仿真值曲线。

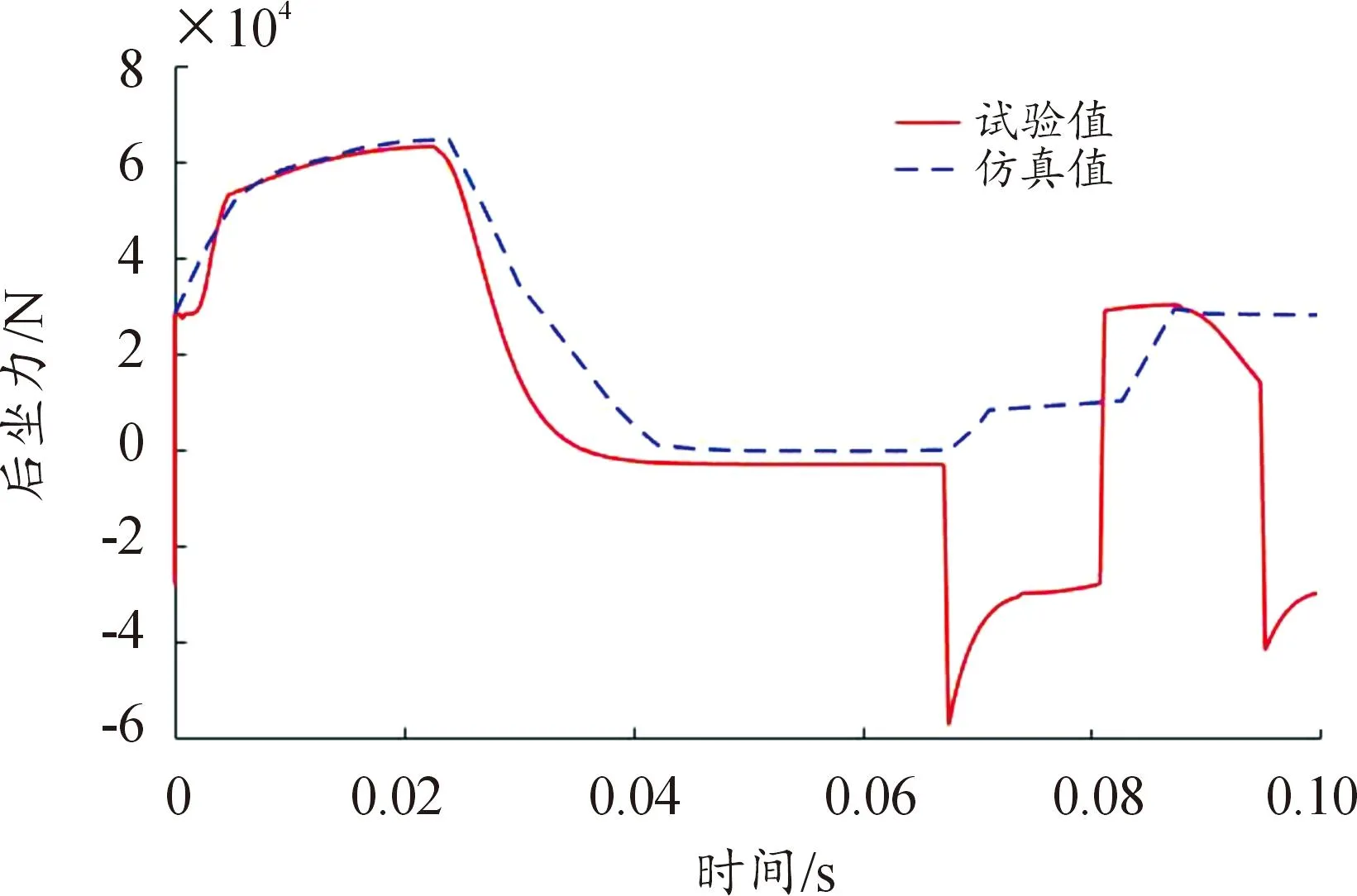
图9 后坐力仿真值与测试值对比图

图10 后坐位移仿真值与试验值曲线

经过计算,后坐阻力相关系数89.3%,而后坐速度相关系数为87.1%,从数据上看出,后坐阻力和后坐位移曲线重合度比较高,说明自动炮发射动力学特性仿真模型有较高的可信度。

2 炮口振动仿真结果

2.1 单发射击仿真结果

对建立的自动炮动力学特性仿真模型进行数值仿真计算,仿真工况为:高低射角和方向射角均为0°。下面给出弹丸出炮口瞬间及单发射击循环周期内的弹丸及炮口动态特性仿真结果。

2.1.1弹丸出炮口瞬间仿真结果

弹丸出炮口瞬间仿真过程如图11所示,由图11可看出,击发后4.2 ms,弹丸已到达炮口位置,这与内弹道计算结果基本吻合。仿真结果显示,弹丸出炮口时,运动为位移2.59 m,速度为1 352.75 m/s,内弹道计算结果分别为2.615 m和1 388.8 m/s,两者计算结果基本一致。另外,从仿真结果可知:本文中计算的自动炮为滑膛炮,弹丸出炮口的速度很高,弹丸质心在高低向和方位向的振动位移、速度及角位移、角速度等物理量都很小,此处不再给出仿真数据。

图11 弹丸出炮口瞬间仿真过程

炮口高低向及方位向振动位移曲线如图12所示,炮口高低向及方位向振动速度曲、线度曲线如图13所示,炮口高低向及方位向振动角速度曲线如图14所示。设置炮口扰动参数:弹丸出炮口瞬间,炮口高低向和方位向的振动位移分别为0.106 7 mm和-0.113 4 mm,振动速度分别为-332.7 mm/s和-21.25 mm/s,振动角速度分别为46.79 deg/s和-179.98 deg/s。根据炮口扰动参数,可估算出弹丸的落点偏差,从而计算火炮射击密集度。

图12 炮口高低向及方位向振动位移曲线

图13 炮口高低向及方位向振动速度曲线

图14 炮口高低向及方位向振动角速度曲线

2.1.2单发射击循环周期内炮口振动仿真结果

炮口高低向及方位向振动位移曲线和振动速度曲线分别如图15、图16所示。

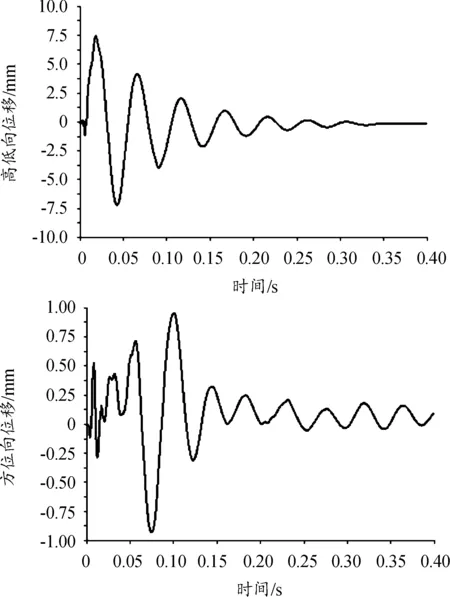
图15 炮口高低向及方位向振动位移曲线

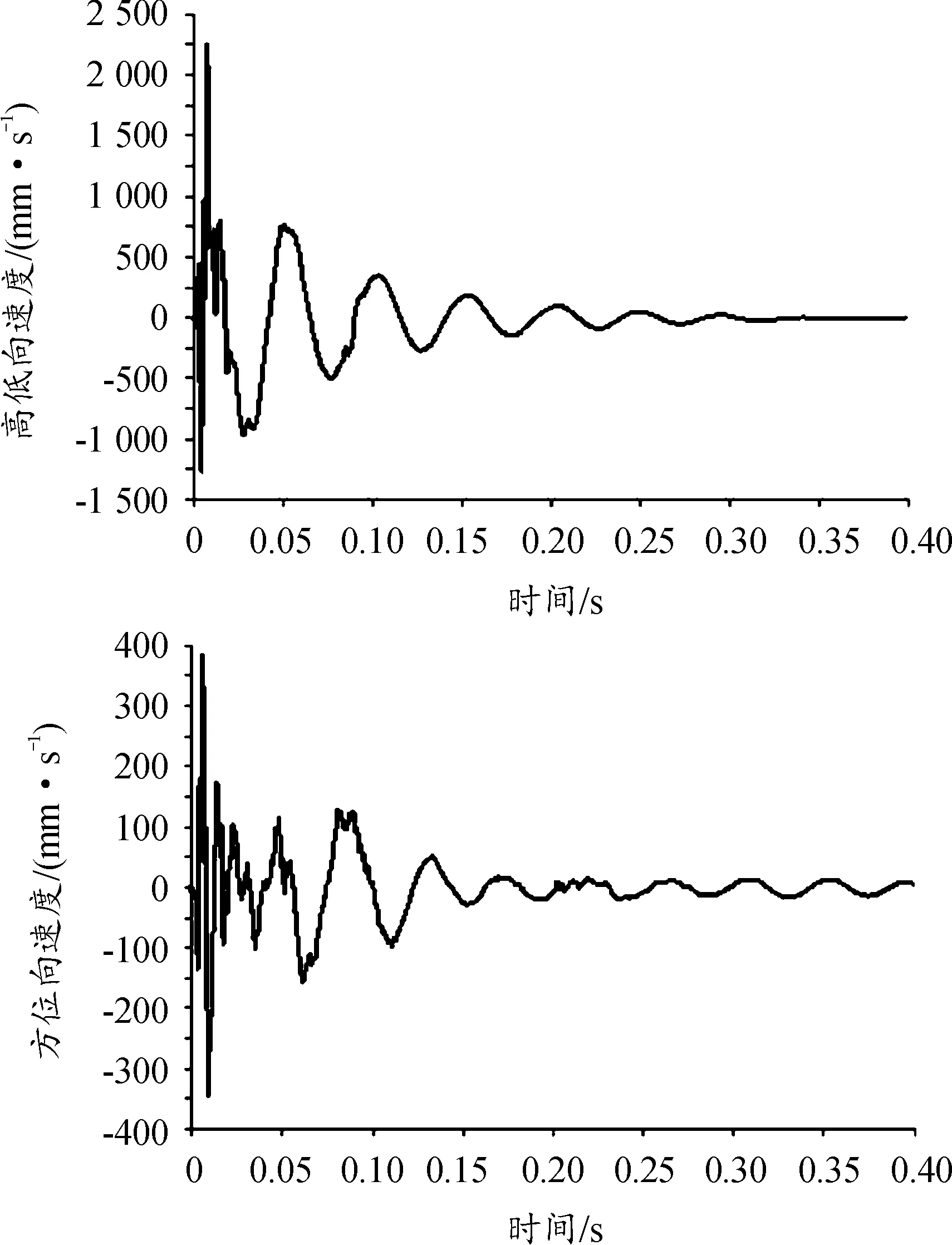
图16 炮口高低向及方位向振动速度曲线

从图15、图16可知:在一个射击周期内,炮口高低向的振幅和振动速度大于方位向,但高低向振动在下一个射击周期开始前能趋于稳定,方位向的振动在下一个射击周期开始前没有完全恢复,前一发弹的射击对下一发弹产生一定的影响。

2.2 连发射击仿真结果

对上述自动炮动力学特性仿真模型进行连发射击数值仿真计算,仿真工况为:高低射角和方向射角为0°,射频为150 rounds/min,5连发穿甲弹射击,仿真时采用变步长方法,各发弹丸内弹道时期,取计算步长为0.000 1 s,其他时期步长为0.01 s。

图17—图22为5连发射击过程中,炮口高低向和方位向振动特性图。

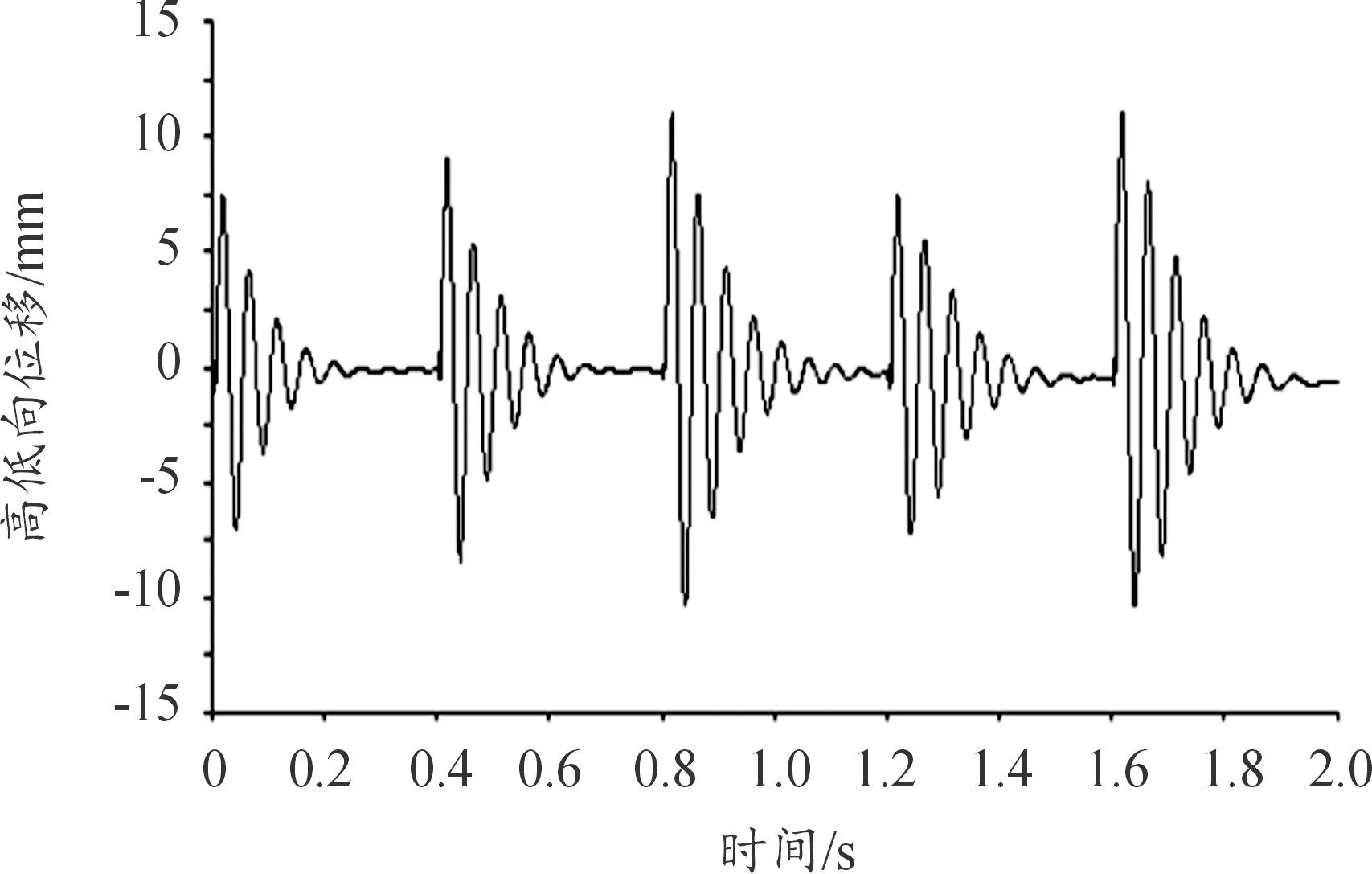
图17 炮口中心点高低向振动位移曲线

图18 炮口中心点方位向振动位移曲线

图19 炮口中心点高低向振动速度曲线

图20 炮口中心点方位向振动速度曲线

图21 炮口中心点高低向振动角速度曲线

图22 炮口中心点方位向振动角速度曲线

由图17—图22可看出:连发射击时,前一发弹丸射击后炮口中心点高低向和方位振动在下一发弹丸射击时没有完全恢复初始状态,身管振动将产生叠加现象,对下一发弹的射击将产生影响。从图17和图18可看出,炮口高低向和方位向的最大振幅较前一发弹射击时都有一些增加,特别是在方位向比较明显,第3发弹击发后的炮口最大振幅较前2发弹射击时有明显的增加;在高低向,随着射弹发数的增加,炮口点的位置向下偏移。因此,设计时应尽量使身管振动在下一发弹丸射击时恢复到最小,保持各发弹丸射击的一致性,提高射击密集度。

3 台架射击密集度计算

自动炮通常用于近距离直瞄射击,立靶密集度是其重要的战技指标之一[14]。根据弹道学理论,在忽略初速偏差和横风等次要因素后,近距离立靶散布的主要影响因素是跳角[15]。

跳角是指弹丸底部(或前定心部)脱离炮口瞬间弹丸速度矢量方向与火炮完成发射准备后炮膛轴线(瞄准线)的夹角,它分为起始跳角和动力跳角,前者是由自重、加工误差、受热不对称等非振动因素引起的身管弯曲造成,而后者是由射击载荷激发的振动因素引起[16]。笔者主要讨论与炮口振动有关的动力跳角。动力跳角的高低分量为高低跳角,方向分量为方向跳角

影响动力跳角的主要炮口振动参数为弹丸出炮口瞬间的振动角位移和振动线速度。立靶散布模型为:

(1)

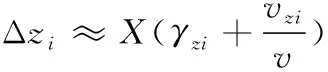
(2)

式(1)—式(2)中:Δyi、Δzi分别为高低和方位向的散布误差;X为立靶距离;γyi、γzi分别为弹丸出炮口时的高低和方位向振动角位移;vyi、vzi分别为高低和方位向的振动线速度;弹丸速度矢量v是弹丸出炮口时弹丸沿炮口法线方向的线速度;θ0为射角。

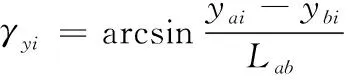
(3)

(4)

式(3)—式(4)中:yai、ybi分别高低向测量点a、b处的振动位移;zai、zbi为方位向测量点a、b处的振动位移;Lab为测量点a、b的距离。

根据以上立靶散布模型估算该自动炮千米立靶散布精度。本文中计算的射击工况为:0°射角,10连发穿甲弹射击,立靶距离为1 000 m。动力学仿真时,记录炮口附近相距300 mm的2个点在每发弹丸出炮口瞬间的高低向和方位向位移。

根据炮口振动特性仿真结果及统计的十连发数据,计算得到十发弹丸的散布误差如表2所示。

根据表2中的数据,并通过式(5)计算表示立靶密集度的高低中间误差和方向中间误差,计算得到该自动炮的千米立靶散布精度为1.368 mil×1.164 mil。

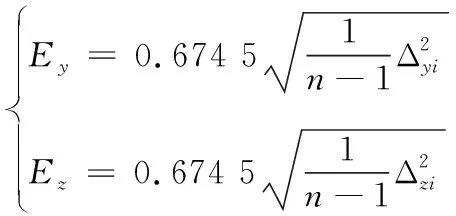
(5)

式(5)中:Ey式中为高低向密集度;Ez为方位向密集度;n为弹药总数。

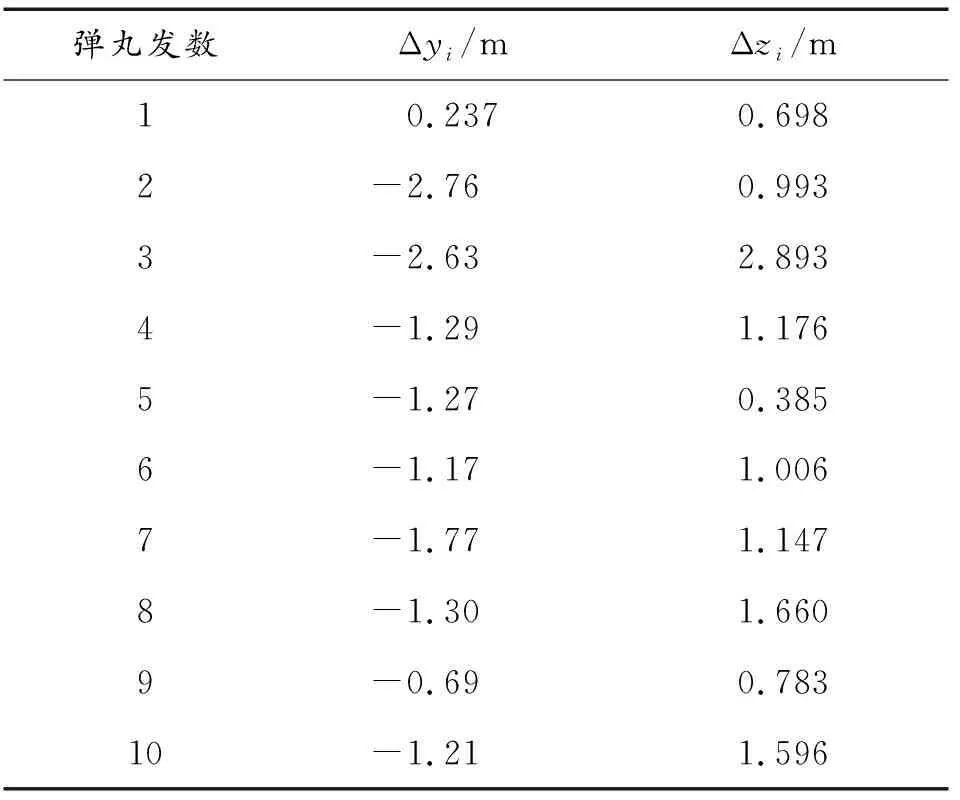
表2 各发弹丸散布误差计算结果

从自动炮射击密集度计算过程可以看出,跳角分为起始跳角和动力跳角,它是近距离立靶密集度的主要影响因素。起始跳角由身管的非振动特性引起,一般难以控制,而动力跳角受炮口振动特性影响,主要包括弹丸出炮口瞬间的振动角位移和振动线速度。因此,在自动炮设计过程中,可以考虑从结构优化层面上有效控制弹丸出炮口时的振动特性,改善弹丸出炮口的一致性,从而提高火炮的射击精度。

4 结论

本文中建立了某自动炮发射动力学特性仿真模型,仿真分析了射击过程中炮口振动特性及规律,并根据炮口特性数据对射击密集度进行初步计算。研究结果表明:

1) 该自动炮建立的虚拟样机模型后坐阻力和后坐位移曲线重合度比较高,模型具有较高的可信度;

2) 一个射击周期内,炮口高低向的振幅和振动速度大于方位向,且前一发弹的射击对下一发弹产生一定的影响,连发时身管振动将产生叠加现象;

3) 经过估算,固定台架上该自动炮的射击密集度为:1.368 mil×1.164 mil。设计时应尽量使身管振动在下一发弹丸射击时恢复到最小,保持各发弹丸射击的一致性,提高射击密集度。

研究结果对火炮射击精度的提高和火炮结构优化具有一定的参考价值。